探索发现——数学教学不可或缺的元素

江苏省苏州市相城区珍珠湖小学 郁小牛

《数学课程标准2011修订版》指出：在数学学习时，“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程”。在处理数学教与学的关系时，教师要“处理好讲授与学生自主学习的关系，引导学生独立思考、主动探索、合作交流，使学生理解和掌握基本的数学知识与技能、数学思想和方法，获得基本的数学活动经验”。对于数学的学习个体来说，探索与发现是学习活动中必不可少的元素。纵观每个人的学习经验，对于一个问题，都要先整理好解决的思路，再按思路探究下去，而整理设计好解决问题的思路就是一个复杂的过程，在这个过程中，要不断地寻找、尝试、调整、验证，直至问题解决。

在数学教学中，应从学生的已有知识水平与经验基础出发，不断发展学生的探索和发现能力，把探索与发现作为学生重要的数学基本元素来培养，让学生在学习数学的过程中，获得更多的知识与技能，更多有价值的感悟和积累，发展学生的数学核心素养。笔者从自己的日常教学探索中提炼了一些感悟与大家分享。

一、基于探索发现，让学生经历知识形成的过程

如苏教版五年级数学下册《分数的基本性质》的教学时，教师使学生通过操作、观察、比较等活动发现分数的基本性质，经历知识的形成过程。课的开始，教师通过让学生比较16÷8 、48÷24 、8÷4这三道除法算式里被除数和除数的变化，看出它们商的大小有什么变化？激活学生的商不变的已有知识经验，为学习分数的基本性质做好准备。

在教学分数的基本性质时，教师让学生利用正方形纸片进行对折，涂色分别表示出二分之一，在此基础上，继续让学生进行对折找出与二分之一相等的分数四分之二、八分之四、十六分之八。教师引导学生观察、比较分数的分子和分母是怎样变化的？并让学生理解为什么分子和分母会发生这样的变化？通过思考，理解分子、分母的份数变化的实质，是1份相当于几份的变化，涂色大小不变，所以变化前后的分数相等。从除法的商不变的规律激活已有认知，以动手折分数、找分数、写等式，探索分数的基本性质，让学生亲历知识的生成过程，让学生在规律的认识分析、推理、概括的过程中，提升学习数学的能力。

二、基于探索发现，让学生经历解法探究的过程

解决问题的过程，是一个相当复杂的过程，在这个过程中，学生要不断探索解决问题的策略。在解决问题时，教师要引导学生分析问题的数量关系，理清解决问题的思路，建立已知与未知之间的联系，最终能解决问题。复杂的问题，总是由若干个简单的问题组合或升级而成的。因此在教学中，教师要引导学生从简单的问题想起，从简单的问题出发，不断尝试、分析，经历解决问题方法的探究过程，在培养学生解决问题能力的同时，发展学生的数学应用能力，提升学生的数学思维品质。

如苏教版五年级数学下册《解决问题的策略——转化》的教学时，教师就是通过引导学生不断对转化的策略进行感悟，重点体会策略的方法、特点、作用，从简单向复杂不断深入的。

在引入策略时，让学生比较两个不规则图形的面积哪个大一些？在没有方格纸对比的情况下，学生初步感知两个图形的特点。增加方格纸后，让学生仔细观察两个图形的特点，进行数方格比较或图形转化变形比较得出面积同样大。以平移和旋转等方法对图形进行转化，让学生体验了转化策略的运用过程。由这个简单的问题，教师适时引导学生联系解决问题的过程，把具体的方法上升到转化策略，体会转化策略的特点，理解由复杂到简单的转化过程，充分体会转化过程中的什么变了，什么没有变。借助于外在显性的解决问题的策略过程，发展学生对内隐的策略数学思想的领悟，不断挖掘学生解决问题策略的数学方法和数学思想。

三、基于探索发现，让学生经历反思归纳的过程

在数学学习的过程中，教师引导学生经历反思、归纳的过程，不仅可以培养学生及时回顾过去、形成良好认知的意识，让学生正确理解并掌握知识与技能，感悟数学方法和数学思想，又能让学生对现有知识进行总结，指向未来的学习活动，把零散的、不成系统的认知通过整理、归纳形成良好的认知结构，使数学知识由量的积累向质的飞跃进行提升。

如苏教版五年级数学下册《解决问题的策略——转化》例2的教学时，教师放手让学生思考，呈现出不同层次的解决问题的方法。如：

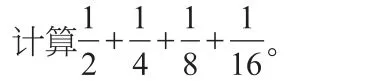
可以通分进行计算，也可以化成小数进行计算，还可以通过画图将原式变成1－进行计算。在学生交流各种解决方法后，教师及时引导学生进行反思，沟通多种方法之间的联系，突出各种不同方法的本质。这样不仅让学生体会到解决问题的转化策略，突出多样的数学方法，而且感悟转化和数形结合的数学思想，把握认知的本质，使学生的数学智慧得以增长。

综上所述，数学学习的活动过程是一个让学生展开数学思考、自主探究、不断内化知识、形成技能、感悟数学思想和数学方法的过程。在数学教学中，教师要从学生已有的认知基础和经验出发，引导学生经历知识生成的发现过程、经历探寻解决问题的解法过程、经历反思归纳的过程。在学生学习数学知识的过程中，教师引导学生建立丰富的数学表象，增强数学学习的活动经验，促使学生主动发现、主动思考、主动建构知识，不断有效发展学生的数学素养，增长学生的数学智慧。