光电稳瞄系统的瞄准线姿态补偿算法

任元斌，吴玉敬，韩 瑞，王 璞，刘小强

(西安应用光学研究所, 西安 710065)

瞄准线稳定与跟踪系统(光电稳瞄系统[1])是多种光电成像系统的核心装备，可以完成对地观测，图像信息收集，测绘等任务。它通常固连在其所在的载体上(飞机，舰船等)，能抵抗外部扰动并保持系统内部成像传感器惯性稳定。

光电稳瞄系统的稳定和瞄准功能实现的核心在于瞄准线的惯性稳定和准确指向。目前光电稳瞄系统是通过在系统的内框架安装陀螺仪，用陀螺仪敏感陀螺轴上的角速度，并以此作为反馈实现惯性稳定。大多数光电稳瞄系统采用双轴陀螺，分别敏感其方位和俯仰方向的角速度信息。但当光电稳瞄系统所搭载的载体发生三轴角运动和线运动时，其双轴陀螺将无法完全获取全部的运动信息，因此无法保证瞄准线的准确指向。此时就需要结合光电稳瞄系统的载体惯导信息，去计算光电稳瞄系统的正确指向。

之前的瞄准线补偿算法，大多是对地理系下东向和北向轴的载体线性运动速度进行补偿，并未将载体发生的三轴角运动和线运动信息全部包含进去。故适用范围有限，在载体频繁做三轴角运动时和所在高度剧烈变化时误差较大。且传统的通过惯导数据计算瞄准线指向的方法是欧拉旋转法，该方法运算复杂，且存在奇异点，适用性不强。

本研究从刚体一般螺旋运动理论出发，结合光电稳瞄系统所在载体的惯导数据，使用四元代数描述了光电稳瞄系统随载体的运动。为使瞄准线方向不受载体运动影响，求解了一次一般螺旋运动后光电稳瞄系统所需调转的三轴姿态角度，免去了使用欧拉旋转带来的复杂矩阵运算，易于工程实现。为三轴光电稳瞄系统提供了新的理论计算视角，拓宽了瞄准线姿态补偿方法的适用范围。

1 基础理论

四元数[2-3]可看成是对复数的扩展，一个四元数q的定义如下：

q=a+bi+cj+dk

(1)

其中i2=j2=k2=-1，若a2+b2+c2+d2=1，q称为单位四元数。

记Qu为全体单位四元数组成的集合，Qu与酉群SU2同构，且是SO3群的双覆盖。SO3群是空间中所有姿态旋转变换组成的集合。

对偶四元数[4]定义为

(2)

其中：p和q都是四元数，p称为实部，q为对偶部；ε为对偶算子，ε2=0且ε≠0。

所有单位对偶四元数组成的集合DQu是刚体姿态变换群SE3的双覆盖。SE3群是空间中所有姿态旋转和平移变换组成的集合。

(3)

sinθ=2(q0q2-q1q3)

(4)

(5)

四维球面线性插值[6]是在两个单位四元数q1和q2之间的弧线函数，插值公式为

(6)

2 问题描述

站心坐标系Ot-XtYtZt：是与大地表面固连的地理坐标系，以靶目标观测点处为原点Ot。Xt，Yt，Zt分别指向东向，北向，天向。

载体导航坐标系Ob-XbYbZb：是与光电稳瞄系统所搭载载体固连的地理坐标系，以载体质心为原点Ob。Xb，Yb，Zb分别指向东向，北向，天向。通常载体导航系的质心和光电稳瞄系统的质心不在同一位置，此处为简化处理，假定载体和光电稳瞄系统为同一质心。

瞄准线坐标系Ol-XlYlZl：是与光电稳瞄系统质心固连的坐标系，以光电稳瞄系统质心为原点Ol，Xl轴为以质心为出发点，与瞄准线重合的射线，与光电稳瞄系统的横滚轴重合，Yl，Zl分别为光电稳瞄系统的俯仰和偏航轴。

不失一般性假设瞄准线坐标系初始时刻和载体导航坐标系Ob-XbYbZb相互重合。随后经历一次旋转，得到初始时刻的瞄准线坐标系Ol-XlYlZl，如图1所示，此时瞄准线指向站心坐标系的原点Ot。

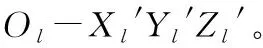
图1 瞄准线变化示意图

3 问题分析和求解

(7)

由式(8)可以解得旋转过程的姿态四元数

(8)

写成矩阵形式为

(9)

其中ωx，ωy，ωz为惯导所测量的载体坐标系三轴的角速度。对此过程q进行归一化为单位四元数，即得到qr。

(10)

(11)

(12)

(13)

(14)

导航坐标系下此三点所成平面的方程为

Ax+By+Cz+D=0

(15)

各系数根据行列式求得：

记F=Ax+By+Cz+D

该平面通过原点处的法向量为

(16)

将以上法向量单位化为单位法向量：

(17)

构造Grassmenn行列式

(18)

(19)

其中各个系数均为Grassmenn行列式的子式，

(20)

根据plüker坐标空间直线所成角度公式

(21)

(22)

该数用q2表示

(23)

其中

(24)

根据四元数到欧拉角的转化公式将qi转化，得到在载体导航系下要使瞄准线指向原目标所需调转到的三轴姿态角为[7-13]：

(25)

θt= arcsin(42(qt 0qt 2-qt 1qt 3))

(26)

(27)

若涉及多次一般螺旋运动可使用上述步骤重复累计计算。

欲寻找q0到qt的最短路径，可用单位四维球面线性插值[14-15]，初始时刻q0到qt的四维球面线性插值为

(28)

其中t∈(0,1)，μt为q0与qt所成夹角。

4 计算实例

图2 机载光电稳瞄系统瞄准线变化示意图

根据上节理论， 计算得到平移带来的旋转量，平台需要以下单位四元数表示的旋转量来补偿

经计算在载体导航坐标系下的稳瞄平台所需的姿态调转到的四元数表示为

qt=q2∘q0=(0.560 1 -0.140 0 0.700 1 -0.420 1)

下面使用Matlab仿真验证上述实例计算过程。在(2，1，2)位置时刻时，瞄准线的单位矢量是由单位矢量(1，0，0)(用纯虚四元数表示为(0，1，0，0))经过由q0表示的一次旋转得到，旋转后的瞄准线向量为

Matlab计算结果用纯虚四元数表示为：

在(1，2，2)位置时刻时，瞄准线的单位矢量是单位矢量(1，0，0)经过由q2∘q0表示的姿态旋转得到，旋转后的瞄准线向量为

Matlab计算结果用纯虚四元数表示为

根据式(25)、式(26)、式(27)计算得载体导航坐标系下的光电稳瞄系统最终所需调转到三轴姿态角表示为

ψt=219.5°,θt=41.81°,φt=92.59°

图3是四维球面线性插值给出的从起始时刻到末端时刻的最优调转路径。图3 (a)为航向方向姿态角度的调转路径规划图，图3(b)为俯仰方向姿态角度的调转路径规划图，图3(c)为横滚方向姿态角度的调转路径规划图。图3中横轴表示采样步长，纵轴表示姿态调转时三轴姿态应在采样点同时调转到达所规划的角度。

图3 机载光电稳瞄系统三轴姿态角度规划示意图

5 结论

从四元代数理论角度出发，求解了光电稳瞄系统在随载体做一般运动时的瞄准线指向问题，提出了一种全方向的瞄准线补偿方法，拓宽了瞄准线补偿方法的适用范围，并以机载光电稳瞄系统为例，对该方法进行了验证。该方法可应用于飞机，舰船等姿态稳定系统上，仅需结合载体惯导信息，实现光电稳瞄系统的视轴指向解算。该方法采用四元代数运算，免去了复杂的矩阵变换，便于实现程序代码并将代码运行在嵌入计算机内重复迭代计算。经过仿真计算验证，可知在经历载体运动后，应用本研究的方法能正确计算系统指向目标所需到达的姿态角度，通过姿态调转达到消除瞄准线偏移的目的。

[1] 纪明.多环架光电稳定系统及分析[J].应用光学,1994,15(3):60-64.

[2] CHOU J C K.Quaternion Kinematic and Dynamic Differential Equations [J].IEEE Transactions on Robotics and Automation,1992,8(1):53-64.

[3] GUI Haichao,GEORGE VUKOVICH.Dual-Quaternion-based adaptive motion tracking of spacecraft with reduced control effort[J].Nonlinear Dyn 2016,83:597-614.

[4] WANG Xiangke,YU Changbin.Unit dual Quaternion-based feedback linearization tracking problem for attitude and position dynamics[J].Systems&Control Letters,2013,62:225-233.

[5] WEN J,KREUTZ-DELGADO K.The attitude control problem [J].IEEE Trans.Autom.Control,1991,36(10):1148-1162.

[6] AHN Jin-su,CHUNG Won-jee,JUNG Chang-doo.Realization of orientation interpolation of 6-axis articulated robot using quaternion [J].J.Cent.South Univ.,2012,19(3):3407-3414.

[7] KONSTANTINOS D.Hand-Eye Calibration Using Dual Quaternions [J].The International Journal of Robotics Research,1999,18(3):286-298.

[8] MILOS IEFRANT,VIJAY KUMAR.Interpolation schemes for rigid body motions [J].Computer-Aided Design,1998,30(3):179-189.

[9] WEN Qiuqiu,XIA Qunli,SU Weixia.Bank-to-Turn Guidance Law with Terminal Impact-Angle Constraint [J].Journal of Aerospace Engineering,2016,29(3):04015067.

[10] YANG X L,WU H T,LI Y,et al.A dual quaternion solution to the forward kinematics of a class of six-DOF parallel robots with full or reductant actuation[J].Mechanism and Machine Theory,2017,107:27-36.

[11] QUINN J A.A Complex Quaternion Model for Hyperbolic 3-Space[M].arXiv preprint arXiv:1701.06709,2017.

[12] ERHARD M,HORN G,DIEHL M.A quaternion-based model for optimal control of an airborne wind energy system[J].ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik,2017,97(1):7-24.

[13] DJAMEL K,ABDELLAH M,BENALLEGUE A.Attitude Optimal Backstepping Controller Based Quaternion for a UAV[J].Mathematical Problems in Engineering,2016(4):1-11.

[14] NEX F,REMONDINO F.UAV for 3D mapping applications:a review[J].Applied Geomatics,2014,6(1):1-15.

[15] 刘小强,邢军智,任元斌,等.基于电流环的改进ADRC在微型光电稳瞄系统中的应用[J].光电工程,2016,43(7):28-33.