采用灰色关联分析方法评估火箭弹毁伤效能

张兰勇，李陇南，陈辉煌

(1.哈尔滨工程大学自动化学院， 哈尔滨 150001;2.东南大学 毫米波国家重点实验室, 南京 210096)

火箭弹是依靠火箭发动机推进的弹药，在现代战争中用于杀伤、压制敌方力量，具有不可替代的地位。火箭弹的毁伤效能受装药的起爆位置、药型罩结构参数、气象等因素的影响[1]。

在实际设计中，合理选取各因素以得到理想的毁伤元，目前还没有切实可行的方法。文献[2-3]通过灰色关联确定了各不确定因素的可信度，有助于显著降低各因素的不确定性；文献[4]利用灰色关联针对空间武器进行作战效能评估。上述文献通过已知信息揭露未知信息，但存在一定局限，有些需要大量实验；有些无法应用于特定场景。

本文采用最小二乘法对火箭弹的毁伤效能和影响因素进行灰色关联分析，进行了多参数比较。通过较少的实验次数，得到最佳参数，达到最佳毁伤效能。在灰色关联分析过程中，通过最大灰色关联度与最小灰色关联度之差，找到对多性能特性影响较显著的因子。

1 灰色关联理论

灰色系统理论就是以“信息部分明确、部分未知”的“小样本、贫信息、不确定性”的灰色系统为研究对象，通过对已知信息生成、开发，提取出有价值的信息，使系统明确化，从而对系统的运行行为、演化规律做出正确描述，揭示未知的信息[5]。

在分析系统时，通常关心的是在众多的影响因素中寻找出主要因素、次要因素、强化发展的因素、起阻碍作用的因素[6]。

灰色关联分析的一般步骤为：首先确定参考序列及比较序列，之后计算两类序列在各时刻的灰色关联系数，然后计算两类序列之间的灰色关联度，最后通过灰色关联度的排序得到灰色关联序。下面简单介绍各个步骤[7]。

1) 数据序列的确定

将能够直接反映系统行为特征且可用于进行灰色关联分析的序列作为数据序列。

定义Zi为第个i系统相关因素，其在序号上观测数据位，Zi(k),k=1,2,…,n。其中，n为观测到的数据量，有：

Zi={zi(k)|k=1,2,…,n}

(1)

若k为时间序号，则Zi为行为时间序列；若k为指标序号，则为Zi行为指标序列；若k为空间分布序号，则Zi为空间分布序列。

2) 数据序列的预处理

在系统中各因素的影响程度不一，各数据的单位、量纲、数量级也可能不同，所以在进行灰色关联分析之前，先要进行数据序列无量纲化。

2 最小二乘灰色关联分析毁伤效能

本节在灰色关联[7]分析方法的基础上，基于最小二乘法的灰色关联度分析，进行火箭弹[8]毁伤效能评估。

首先考虑火箭弹发射各种因素统计分析，包括地形条件、气象条件、弹道条件。具体阐述如下：

地形条件：弹着点位于火炮炮口水平面上；火箭炮位置水平。

弹道条件：全备火箭弹重：66.830 kg；引信重：0.95 kg；发射药重：20.6 kg；火箭弹(包括引信)的外形与图纸要求一致；装药温度：15 ℃；主动段终点速度与比冲量及发动机工作时间2.14 s相吻合。

气象条件：无风,即在任意高度上风速均为零；炮口水平面上的气温(虚度)为：16 ℃，气压为：750 mmHg；气温(虚度)按高度符合标准分布规律。

以上述因素的样本数据为依据，用灰色关联度描述因素间关系的强弱、大小和次序。对于多指标综合评估对象可以把比较序列看成由火箭弹的各项指标值构成的序列。参考序列是一个理想的比较标准，受到距离评估方法的启示，选最佳指标数据和最劣指标作为参考序列。比较各作战方案与最好和最劣方案的关联程度，评估各个方案相互之间的优劣[9]。

根据数据序列的不同特性，灰色相关分析有不同的数据预处理方法。

原序列可表示为：

(2)

若为望小特性，原序列可表示为：

(3)

若为望大特性，原序列可表示为：

(4)

一般情况下，A*方案与正理想方案关联最大，即负理想方案最小，但根据结果有可能产生A1关联正理想方案比A2大，关联负理想方案也比A2大，如图1所示，圆圈表示可行方案域，表示正理想方案，A*表示负理想方案，此时需要利用最小二乘法改进评估结果。具体计算步骤如下所述[11]。

具体步骤如下：

1) 确定作战方案的性能指标体系，其中待评估的方案集，记为A={a1,a2,…,am}；评估方案优劣的指标集，记为C={c1,c2,…,cn}。

2) 由火箭弹的对空射表实验结果得到原始评估矩阵Y，见表1。

3) 数据的标准化处理，即：

(5)

(6)

其中，j为方案号，i为性能指标号，式(5)适用于值越大效用越好的因素属性(如导弹毁伤度)，式(6)适用于值越小效用越好的因素属性(如己方毁伤数)。所有因素进行无量纲化处理，得到评估矩阵。

4) 确定正理想方案和负理想方案。

5) 灰色关联系数计算。对于参考数列X0，比较数列X1,X2,…,Xn，令R=|X0j-Xij|，得到

(7)

对于正理想方案x*=(1,1,1,1,1)的关联系数矩阵为ζ*；

对于负理想方案x-=(0,0,0,0,0)的关联系数矩阵为ζ-。

6) 关联度计算。关联度系数越多，信息越分散，对所有关联系数取平均值，得和的关联度：

(8)

7) 确定评估系数。作战性能优劣的评估由作战效能与理想效果的接近程度判定。

评估系数Ci的定义为

(9)

显然，当Ci=0作战方案为负理想方案时，Ci越接近1，作战方案越接近于正理想方案。对于火箭弹毁伤效能的评估进行定量的评估，由Ci的大小确定。

8) 应用最小二乘法改进后确定评估结果。

定义关联度γ(X0,Xi)，系统的优向量和次向量分别为X*和X-。以与优向量Xj和次向量计算关联系数(取u为0.5)ζi(Xj,X*)和ζj(Xj,X-)，求得关联度。假设Xj为以μj隶属于正理想方案向量，即Xj以(1-μj)隶属于负理想方案向量，利用最小二乘法构造如下目标函数：

[μjγ2(Xj-X-)]2}

(10)

式中，μ=(μ1,μ2,…,μn)为系统的最佳解向量，为使Xj的关联度最小，令一阶导数等于0，结合关联度计算公式，可得：

(11)

然后根据μj的大小对各个方案排序。

3 火箭弹毁伤效能评估仿真

(12)

(13)

按上述同样的方法对每次实验的数据预处理和绝对偏差均计算。表2表示导弹目标毁伤判据，把分辩系数代入式(7)得灰色关联系数。由于气象条件与环境条件对命中概率的影响大，故取ω1=0.3,ω2=0.7，由式(8)计算灰色关联度，其结果如表3。

根据数据处理结果，图2所示18次试验的毁伤概率分布中,可发现第9次实验的设计参数在这18次实验中是一个最佳的射击参数，它使系统的命中失效率最小。

为了获得全局最佳参数，计算每一个影响因子不同水平的平均灰色关联度。其步骤是：1)从表3中找出直交表每一列同一因子水平的灰色关联度值，2)求其平均值。

例如求因子A关联度值可由下式计算：

(14)

对其他射击参数的每一水平的灰色关联度值同样按上述方法计算[12]，计算结果如表3。因此灰色关联度值最大的因子水平就是最佳的射击参数水平。表3中带*的因子水平有较好的射击精度。

这样确定的射击参数为：射击倾角为-109.0毫弧度、弹丸初速为468.1 m/s、弹道下降量为882.6 m等。

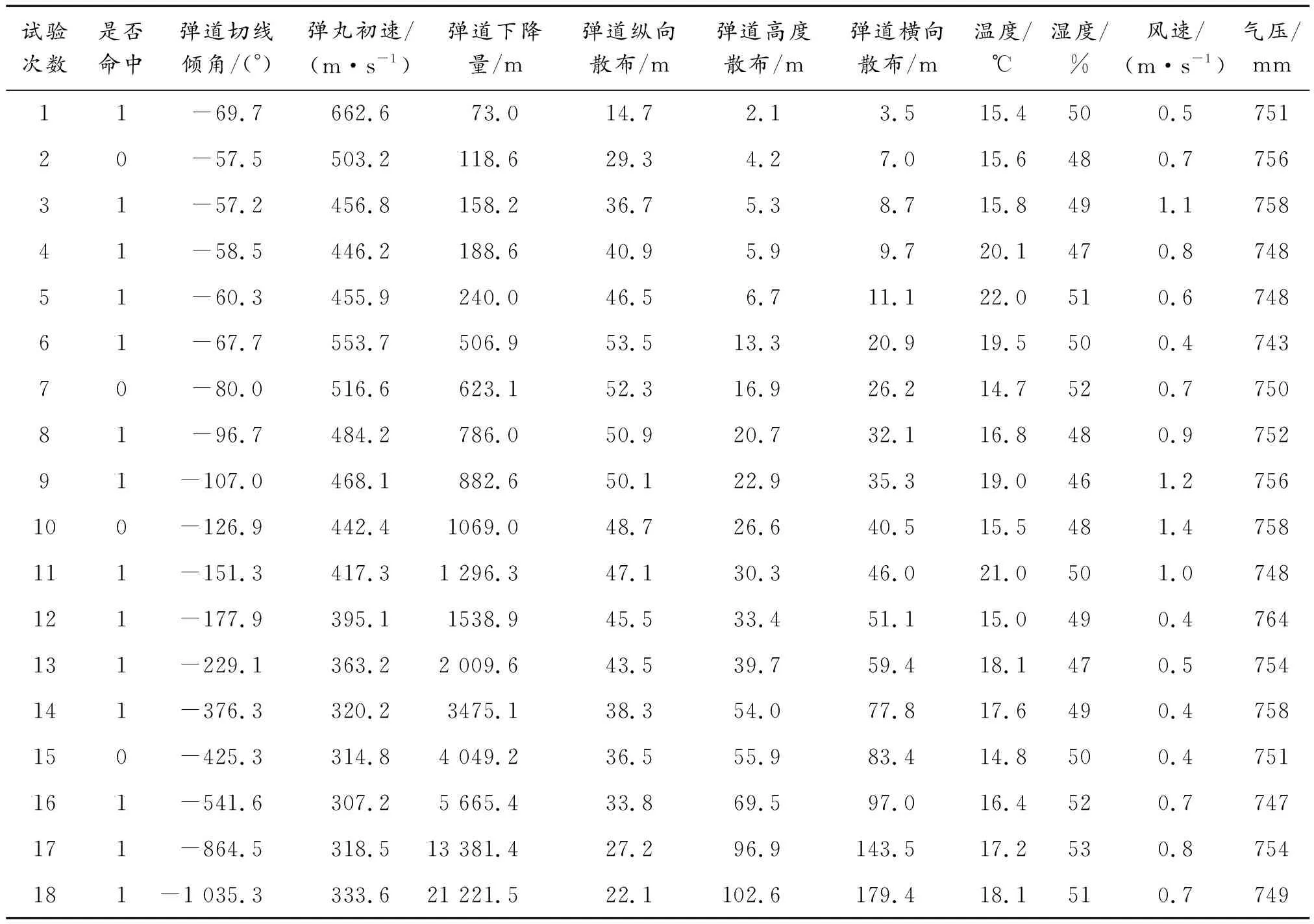
表1 火箭弹弹道基本射表

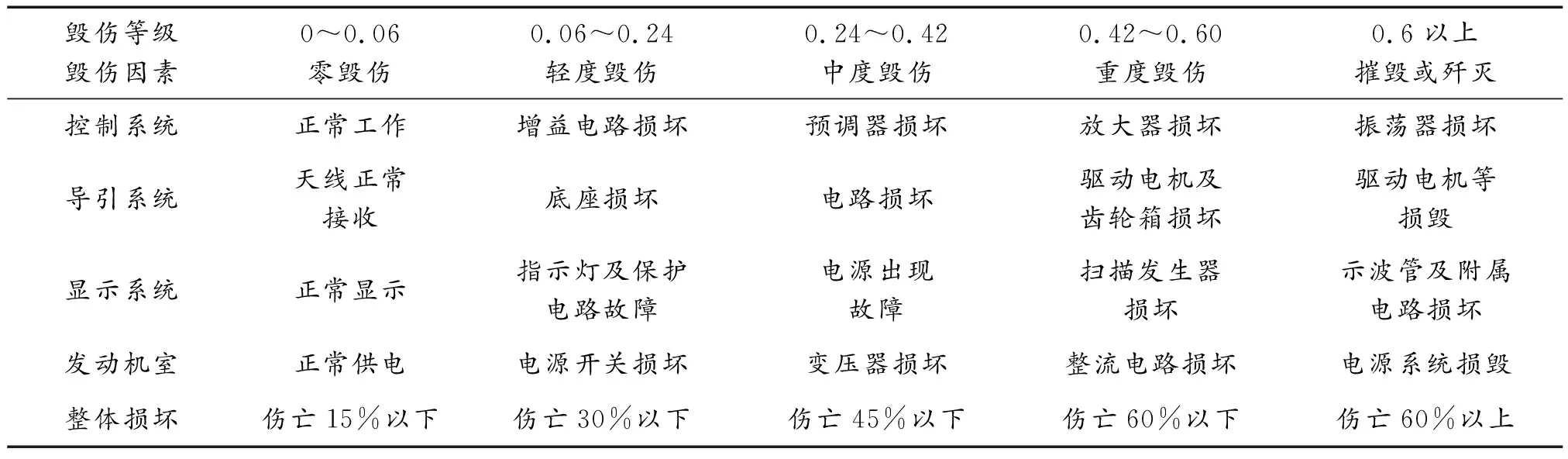
表2 导弹目标毁伤判据

表3 不同因素下的射击参数关联度

表3中，射击参数的最高和最低灰色关联度值之差分别为：弹道切线倾角的最高和最低灰色关联度值之差为 0.054 5、弹丸初速的最高和最低灰色关联度值之差为0.084 8等。比较这些差值能决定影响射击因子的影响程度。这7个差值之间最大差表示影响程度最大的是弹丸切线倾角。影响的排序是：F>D>E>B>A>G>C。

利用灰色关联法对比出的影响因子排序，对影响因素逐个进行调整，对结果进行仿真后，和不调整时进行对比，如图3所示。

从结果可以看出调整影响因素明显减少了低毁伤概率，增加了高毁伤概率；同时调整不同影响因素对毁伤结果的改变程度不同，影响力越大的因素，其调整之后的结果明显，低毁伤概率降低，高毁伤概率增加。从而证明了灰色关联方法的有效性和各影响因子顺序的正确性。

4 结论

本文通过对火箭弹弹着点的散布规律以及破片毁伤目标的能力进行分析，建立火箭弹毁伤概率模型，利用该模型对火箭弹易损性进行仿真分析，并引入灰色关联研究分析炮弹毁伤概率随动能弹丸速度、打击方位角和高低角变化规律。

实验结果表明，本方法有效推测出毁伤效能和各毁伤因素之间的强弱联系，使毁伤效能和各毁伤因素间的关系明朗化；改进了火箭弹的毁伤评估效能，使重度毁伤率(含歼灭)提升了30%；本文提出的灰色关联可以很好地应用效能评估，在明确未知关联中具有重要意义。

[1] 刘凯,冯昌林.箔条火箭弹反导效能评估[J].四川兵工学报,2010,31(3):11-13.

[2] 李鹏,刘思峰.基于灰色关联分析和D-S证据理论的区间直觉模糊决策方法[J].自动化学报,2011,37(8):993-998.

[3] 刘思峰,蔡华,杨英杰,等.灰色关联分析模型研究进展[J].系统工程理论与实践,2013,33(8):2041-2046.

[4] 轩永波,黄长强,王勇,等.基于灰色层次分析法的空间武器作战效能评估[J].空军工程大学学报(自然科学版),2011,12(2):32-37.

[5] 刘思峰,蔡华,杨英杰,等.灰色关联分析模型研究进展[C]//IEEE International Conference on Systems,Man and Cybernetics,Anchorage,Alaska,Usa,October.DBLP,2013:1886-1890.

[6] 王保华,裴益轩,霍勇谋,等. 一种求解火箭防空武器毁歼概率的简便方法[J].兵工学报，2016(4)：751-755.

[7] WANG Q,LIU G,WANG X.Gray correlation degree analysis of controlling factors on coal deformation[J].Energy Exploration & Exploitation,2011,29(2):205-216.

[8] KONG L,JIAO Y,DAI Z.A new substation area protection principle based on gray correlation degree[J].Power System Technology,2014,38(8):2274-2279.

[9] 关成启,杨涤,关世义.导弹武器系统效能评估方法研究[J].系统工程与电子技术,2000,22(7):32-36.

[10] 王志刚,李伟,张振宁.双旋制导火箭弹动力学建模[J].兵工学报,2013,34(7):910-915.

[11] 王军,王兴,胡玉理,等.高能激光对巡航导弹毁伤效能评估与仿真[J].弹箭与制导学报,2013,33(1):93-96.

[12] 刘义,赵春娜,王雪松,等.一种反辐射武器作战效能评估方法[J].兵工学报,2011,32(3):321-326.