基于马尔科夫链的大学生自主学习能力预测方法
刘德春,张秀国,姜 微
(1.南阳理工学院计算机与信息工程学院,河南 南阳 473000; 2.大连海事大学信息科学技术学院,辽宁 大连 116026)
0 引 言
大学生对自主学习能力进行预判是提升自我学习能力的有效方法。自主学习是一种主体驱动,即学习目标自己确定、内容自己选择、计划自定并可以对学习结果进行评估、调控的学习模式[1-3]。对自主学习能力的预测技术可以应用马尔科夫(简称马氏)链、BP神经网络等原理模型。目前,国外对自主学习能力的研究多在能力评估方面,例如,Belski等人[4]提供了一个培养学生自主学习技能的简易程序(TERISSA);Roth等人[5]把心理和教育数据库的系统搜索结果在自我评估报告工具中加以应用。国内有关自主学习的研究,主要在于自主学习评估与涉及学习平台方面的探讨,真正进行学习能力预测的还比较有限。如:刘歌等人[6]用马氏原理分析学生学习成绩状况及趋势,并提供了样本实例;文献[7]用BP神经网络方法构建了深度学习水平预测模型;文献[8]提出了建立在移动学习(M-learning)基础之上的远程自主学习模型;文献[9]使用挖掘等技术结合Web建立了一种个性化学习模型;文献[10-11]在考虑学生的个体差异后把马氏模型引入教学评价机制,通过数学方法分析评估对教师教学和学生学习产生的影响。
本文利用马氏原理短期预测效果精准之特长,以期通过建模与算法实现,对学生自主学习潜在能力进行可操作性强的预测,然后以预测结果对比当前实际学习状态,使被评测者掌握自身潜在学习情况及不足,通过不断自我调整,达到改善提高自身学习能力之目的。
1 马尔科夫链定义与原理
1)马尔科夫链的定义[12]。
设一个随机序列{X(t),t∈T},条件分布函数满足等式:
F(x,t|xn,xn-1,…,x2,x1,tn,tn-1,…,t2,t1)=F(x,t|xn,tn)
即:
P{X(t)≤x|X(tn)=xn,…,X(t1)=x1}=
P{X(t)≤x|X(tn)=xn}
此性质称为马尔可夫性,时间和状态都是离散的马尔可夫过程称为马尔可夫链。若X(t)为离散型随机变量,则马尔可夫性亦满足等式:
P{X(t)=x|X(tn)=xn,…,X(t1)=x1}=
P{X(t)=x|X(tn)=xn}
2) 原理性质。
序列{X(t)}在t+1时刻系统状态的概率分布只与t时刻的状态有关,与t时刻以前的状态无关,可以通过现在状态推演出来;不同状态之间的转移是随机的;设P是系统的状态转移概率矩阵,其中Pij表示系统在时刻t处于状态i,在下一时刻t+1处于状态j的概率,N是系统所有可能状态的个数。状态集中某一个元素包含状态{X(t)}之中某一符号X(ti)的数值,则称该元素集合形成了一个状态序列Si。
3) 状态转移概率。
马尔科夫链特性可以用状态转移概率来描述,对于有限状态空间,则转移概率分布可以表示为一个具有(i,j)元素的矩阵,称之为“转移矩阵”:
Pij=P(Xn+1=i|Xn=j), i,j∈E
离散状态空间中k步转移概率的积分即为求和,可以对转移矩阵求k次幂来求得。就是说,如果是“一步转移概率矩阵”,就是k步转移后的转移矩阵。它满足:
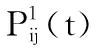
2 建立基于马氏原理的自主学习能力预测模型
设定已知某学生的当前状态,在此基础上对下一时段自主学习的能力状态进行预测。人的学习能力是指人某一个时期或一个时段的状态反映,通常在短时间内是一种比较稳定的状态,因此在实际中有必要把理论上的时刻延伸为时段,这里以2周时间作为考察标准进行分析研究。根据马氏原理可知,状态的变化可以用状态转移概率矩阵来反映,通俗地说就是该学生由上一时刻转为下一时刻状态的概率所组成的矩阵,预测模型科学与否的关键就在于求得相对准确的状态转移概率矩阵。当时间时段为Ti,如果在此时段利用概率矩阵得到的相对预测误差很小,即概率矩阵达到稳定状态,那么就可以据此对下一时刻即本文研究的时段对象进行预测,其理论依据就是马尔科夫链性质所述:下一时段Ti+1的学生自主学习状态与Ti时段以前的状态无关,只考查当前时段Ti的状态情况,从而可求得预测结果。
由以上描述可以把预测模型的建立过程归纳概括为3个主要步骤:1)定义自主学习的初始状态;2)求解状态转移概率矩阵;3)检验预测误差。具体实现操作:定义初始状态时一次主选12项自主学习数据指标作为当前初始状态向量;通过优化二次规划模型求解状态转移概率矩阵,依状态转移概率矩阵预测自主学习能力;利用模型要求,取实际考查数据与历史预测结果进行平均相对误差检验,从实际结果对比预测的准确度,根据平均相对误差检验调整状态转移概率矩阵,当误差不满足要求时,增大历史调查样本次数,然后再次求解转移概率,一直进行下去直至求得一个相对稳定的误差状态。
建立的预测模型流程如图1所示,预测过程详细说明如下:
第1步定义自主学习初始状态。
把自主学习能力影响因素(Influencing Factors)定义为IF,把策略(Strategy)记为ST,把动机(Motivation)记为MT,则影响因素的集合为IF,IF={ST,MT},其中:ST={GM,LH,LP,LS,LE,LM},MT={SE,IG,LC,LEG,LSM,LA}。
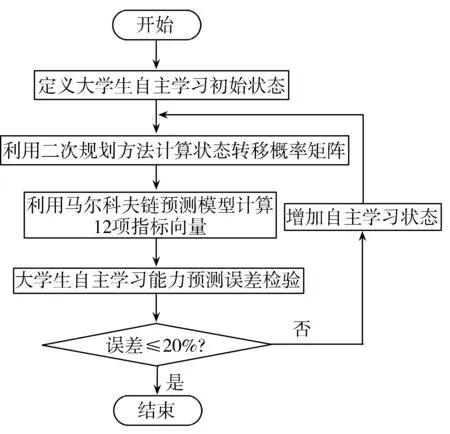
图1 大学生自主学习能力预测过程
基于以上定义,把调查问卷(调查对象自主学习能力)各分项影响因素得分的量化值与问卷总分作比值后的占比集合如下式所示:
影响集合:S_IF={S_ST,S_MT}
其中,
策略项:S_ST={S_GM,S_LH,S_LS,S_LP,S_LE,S_LM}
动机项:S_MT={S_SE,S_IG,S_LEG,S_LC,S_LSM,S_LA})
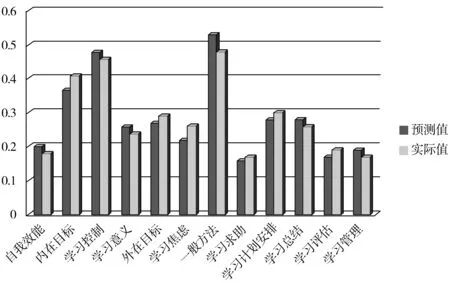
相应地,设考察n个时段,共有n个数据状态:{S1,S2,…,Si,…,Sn},i为当前第i(i 第2步计算状态转移概率矩阵。 预测模型的建立需要把问题求解分成有限个状态的集合,而状态转移概率矩阵的获得过程是,由上一状态转为下一状态的概率形成的矩阵,其中状态转移概率矩阵是马氏预测模型中最至关重要的一步[13]。对于时间状态序列S={S1,S2,…,Sn},每两两状态之间转移过程如下: Si→S1,Si→S2,…,Si→Si,Si→Sj,Si→Sn 假定经历k个时间点之后,当前时间序列状态为Si转移状态变为Sj,则条件概率在状态转换后可以用公式(1)表示: (1) 当k=1时,式(1)可写为: Pij=P{X(m+1)=Sj|X(m)=Si}, Si,Sj∈S (2) 于是得到一步转移概率矩阵如公式(3)所示: S1S2… Sn (3) 矩阵满足: Pij(n)≥0, i,j∈I (4) ∑j∈IPij(n)=1, i∈I (5) 据前所述,考查的下次自主学习状态只与当前状态有关,故而选择一步状态转移概率矩阵求解,对矩阵的求解使用二次规划方法,下面简述二次规划法基本原理。 二次规划是计算数学与运筹学相交叉的一门学科,考虑二次规划最优化问题[14]: (6) 其中,f(x)是目标函数,gi(x)(i=1,2,3,…,k)是对不等式进行约束,hj(x)(j=1,2,3,…,m)是对等式进行约束,k和m是相应的约束数量。 假设目标函数和约束函数满足:f:Rn→R,gi:Rn→R,hj:Rn→R,且f(x),gi,hj是在可行域任意一点x*上连续可微的,如果x*是一个局部极小值,则一定有一组常数λ≥0,ui≥0(i=1,2,3,…,m),vj≥0(j=1,2,3,…,l),满足公式(7): (7) 以下利用该方法求取一步状态转移概率矩阵最优解。 取自主学习的时间序列为Si(i=0,1,2,…,m),一步状态转移矩阵P=(Puv)n×n,由于Si+1与SiP存在一定误差,并不能始终保持一致,故本模型强调消除两者之间的误差平方和,建立优化模型如公式(8)所示: (8) 其中,Q=Si+1-SiP,此模型是二次规划优化模型。状态转移矩阵模型求解算法可通过C++或Matlab编译实现。 第3步建立Markov链预测模型。 (9) 其中,Si可表示为: Si=(S_SEi,S_IGi,S_LCi,S_LSMi,S_LEGi,S_LAi,S_GMi,S_LHi,S_LPi,S_LSi,S_LEi,S_LMi) 第4步自主学习能力预测误差检验。 如前所述建立的预测模型可以得出下次(后一段)数据的预测结果,把它与实际调查数据结果进行对比分析,就可以判定误差的大小(差异度)。设第i+1次的实际数据序列表示为: Si+1=(S_SEi+1,S_IGi+1,S_LCi+1,S_LSMi+1,S_LEGi+1,S_LAi+1,S_GMi+1,S_LHi+1,S_LPi+1,S_LSi+1,S_LEi+1,S_LMi+1) (10) 与其相对应的Markov链模型预测后的预测值序列为: (11) 进而得到残差数值序列: ε=(ε(1),ε(2),…,ε(n)) (12) (13) 当k≤n时,得: (14) 式(14)为模型在k点的相对预测误差。 (15) 式(15)为平均预测相对误差。 实验选用MyEclipse IDE和Matlab对基于马尔科夫链的大学生自主学习能力预测模型进行实现。首先,采用二次规划法求解状态转移矩阵;然后,在预测算法中打成jar包并将计算机程序封装成一个函数;接下来,在MyEclipse中导入该jar包并使用Java代码调用程序中的函数来实现预测功能。 图2展示了预测模型的具体实现流程。首先,载入自主学习的12项指标数据向量组,列出向量组的二次规划模型表达式;然后,利用Matlab函数Fmincon求出状态转移概率矩阵;接下来,定义自主学习12项指标数据初始向量,利用初始向量和上面求出的状态转移概率矩阵求出12项指标预测向量;最后,利用12项指标的预测值与实际值来计算平均相对误差,判断误差是否在20%之内,如果在则结束预测,否则增加历史调查数据,继续求解,直到达到一个误差相对稳定的状态。 图2 大学生自主学习能力预测模型实现流程 以某校某同学的一年内自主学习状态评估指标为例,经过对往期考查数据个数的不断调整,利用已有数据对下一次的自主学习状况进行预测分析实验,最终确定统计13次真实数据,其中前12次数据作为模型训练样本数据,把第13次问卷调查数据作为实际数据与预测结果对比,计算出较小的相对平均误差,利用Matlab仿真计算对模型公式进行求解,给出预测过程实现及预测结果分析和等级评估。本案例所采用的数据是由课题组通过问卷调查取得,具体参见文献[15]。 如前所述,所统计的某学生自主学习的历史数据信息12次,每个数据项为数据问卷调查的单项得分与卷面总分的百分比,反映了该同学自主学习能力各指标的总体分布情况。由于在第12次时该学生状态转移概率矩阵基本处于平稳状态(即根据第11次数据预测第12次能力状态数据时,所得计算预测误差为最小值,从而可求解出稳定的概率矩阵),前12次基本数据情况汇总后,如表1所示。 根据表1提供的自主学习实际数据,应用公式(9)进行求解,可求出转移概率矩阵P。将表1中的最后一行即第12次的状态序列作为初始状态,使用S′(1)=S(0)P来预测第13次的自主学习能力,结果如表2所示。 表1 前12次自主学习的实际值 次数自我效能内在目标学习控制学习意义外在目标学习焦虑一般方法学习求助学习计划安排学习总结学习评估学习管理10.220.350.430.200.190.160.560.140.280.250.180.1620.200.370.450.210.230.200.580.160.300.220.150.1230.150.330.400.150.160.130.500.100.220.220.150.1340.170.340.410.160.170.140.510.120.230.230.160.1550.200.360.440.250.150.120.530.100.250.220.120.1460.270.300.460.200.250.300.600.220.330.300.230.2070.250.280.440.180.230.280.580.200.310.290.210.1780.220.260.420.160.210.260.560.180.280.250.190.1590.200.240.400.140.190.230.520.160.240.230.170.13100.240.260.430.180.230.240.540.170.290.270.200.16110.250.320.460.240.230.270.600.200.170.200.220.20120.190.290.460.270.220.170.570.210.250.220.200.13 表2 第13次的自主学习能力预测值 情况说明自我效能内在目标学习控制学习意义外在目标学习焦虑一般方法学习求助学习计划安排学习总结学习评估学习管理预测值0.200.370.480.260.270.220.530.160.280.280.170.19实际值0.180.410.460.240.290.260.480.170.300.260.190.17 对该学生的能力状态实际情况和预测情况进行对比,结果如图3所示。 图3 预测值和实际值对比 利用公式(15)进行求解、计算平均相对误差,得出相对误差结果为8%,远小于阈值,因此符合检验标准。 经分析研究提出大学生自主学习能力预测模型,通过实践检验并结合预测结果与实际数据的比较分析,采用直观图表方式的结果对比,表明其能够预测和反映自主学习能力的客观情况。建立的数学模型描述精确,预测结果稳定、高效。所提供的算法平台能够应用于大学生自主学习能力全程预测,分析结果有助于发现学习能力之不足和缺陷,从而及时调整自我状态、保持高效的自主学习能力,因此算法模型可应用到知识学习类软件的开发当中。 参考文献: [1] 亓丽媛. 大学生自主学习调查研究[D]. 金华:浙江师范大学, 2012. [2] 余文森. 略谈主体性自主学习[J]. 教育探索, 2001(12):62. [3] 庞维国. 自主学习学与教的原理和策略[M]. 上海:华东师范大学出版社, 2003:112-113. [4] Belski R, Belski I. Cultivating student skills in self-regulated learning through evaluation of task complexity[J]. Teaching in Higher Education, 2014,19(5):459-469. [5] Roth A, Ogrin S, Schmitz B. Assessing self-regulated learning in higher education: A systematic literature review of self-report instruments[J]. Educational Assessment Evaluation & Accountability, 2016,28(3):225-250. [6] 刘歌,刘凤祥,杜春雁,等. 运用马尔科夫链进行学习状态变化趋势分析的一种方法[J]. 中国教育技术装备, 2015(18):96-98. [7] 尹桐,杜树杰. 基于BP神经网络的大学生深度学习水平预测模型构建[J]. 中国教育信息化, 2015(23):72-75. [8] 熊小猛,陈中. 基于M-learning的远程自主学习模型建构[J]. 中国医学教育技术, 2007,21(1):71-73. [9] 王晖,王瑜,焦永革,等. 计算机与教育:应用促进学与教创新[C]//全国计算机辅助教育学会第十三届学术年会论文集. 北京:中国人工智能学会计算机辅助教育专业委员会, 2008:3. [10] 马睿瑄. 马尔科夫链模型在发展性学生评估中的应用研究[D]. 呼和浩特:内蒙古师范大学, 2014. [11] 朱丽波. 马尔科夫链模型在学生学习评价中的应用[J]. 内蒙古师范大学学报(教育科学版), 2015,28(8):115-117. [12] Norris J, Peres Y, Zhai A. Surprise probabilities in Markov chains[J]. Combinatorics, Probability and Computing, 2017,26(4):603-627. [13] Chotard A, Auger A, Hansen N. Markov chain analysis of cumulative step-size adaptation on a linear constrained problem[J]. Evolutionary Computation, 2015,23(4):611-640. [14] 李学良. 炼油厂混合整数二次规划调度模型的算法研究[D]. 济南:山东大学, 2012. [15] 姜微. 基于iData的大学生自主学习能力预测模型研究[D]. 大连:大连海事大学, 2017.





3 模型实现

4 案例分析
4.1 案例描述
4.2 预测过程



4.3 预测误差分析
5 结束语

