基于加权中值滤波的MST立体匹配算法

赵大成，许道云

(贵州大学计算机科学与技术学院，贵州 贵阳 550025)

0 引 言

自从2002年Scharstein等[1]提出立体匹配算法的分类与评价以来，大多数的立体匹配算法被分成4个部分：1)匹配成本；2)成本聚合；3)视差优化；4)视差求精。全局立体匹配算法[2-4]主要是采用全局优化建立能量函数方法估计视差，通过最小化全局能量函数得到最优视差值。相对于全局立体匹配算法，局部立体匹配算法是在限定的范围内计算聚合代价，因此，速度优于全局立体匹配算法。传统的自适应窗口方法[5]和自适应权重方法[6]都是在局部窗口中计算匹配成本，在视差计算上通常陷入局部最优的缺陷，而且窗口过大易出现边界模糊，窗口过小易出现噪点。Hirschmuller等[7]提出了减小边界误差的方法，在经典算法上，只需要限制成本聚合阈值就能够有效地减小误差。Yang Qingxiong[8]提出了MST最小生成树的立体匹配算法，该方法基于全局最小生成树的代价聚合方法，兼具了局部匹配算法速度快和全局匹配算法精度高的优点，但对弱纹理区域和边缘区域效果一般。Ma Ziyang等[9]提出了恒定时间加权中值滤波在立体匹配中的应用，有效地提高了立体匹配中图像边缘的准确率。Li Linchen等[10]提出了多个最小生成树的三维成本聚合的立体匹配算法，通过使用三维坐标定义视差图，结合多个最小生成树和块匹配[11]，有效地改善了MST不平滑和误匹配。Hamzah等[12]提出迭代引导滤波和图像分割的立体匹配算法，通过实验组合各种算法，找到最优的匹配效果。

上述的立体匹配算法都极大地提高了匹配效果，但MST最小生成树立体匹配算法仍然存在匹配成本不合理，聚合阈值和后处理不够准确等不足。针对以上算法的不足，本文提出一种改进的最小生成树立体匹配算法。本文主要有2点贡献：提出一种改进的最小生成树匹配成本和提出加权中值滤波后期视差优化方法。

1 改进最小生成树立体匹配算法

本章提出一种新的匹配成本算法，介绍MST算法如何在图像中建立最小生成树，并分析通过2次遍历就能计算所有的聚合代价值，最后用图像对比算法的差异。

1.1 新匹配成本

匹配成本是用来比较左右图像对应像素点的差异，左右图像对应像素匹配成本越小，那它们很有可能是相互匹配的点。本文定义的每个像素点的匹配成本Cd(p)是由图像水平方向的梯度Gx和像素颜色值I(p)决定，在此基础上为了扩大匹配成本差异，改进匹配成本，新的匹配成本Cd(p)可表示为：

Cd(p)=exp (α·‖I(p)-I(q)‖+(1-α)Gx)

(1)

其中，d代表视差，α为固定的参数，p表示左图像素点，q表示右图对应的像素点。

1.2 MST最小生成树

原始图像被视为网格无向图。每个像素当作一个节点，每个节点都与相邻的像素点相连。设s和r是一对相邻像素，s和r之间的连接权重w(s,r)可表示为：

w(s,r)=w(r,s)=‖I(s)-I(r)‖

(2)

其中，I(s)和I(r)表示图像RGB三个通道的颜色值。

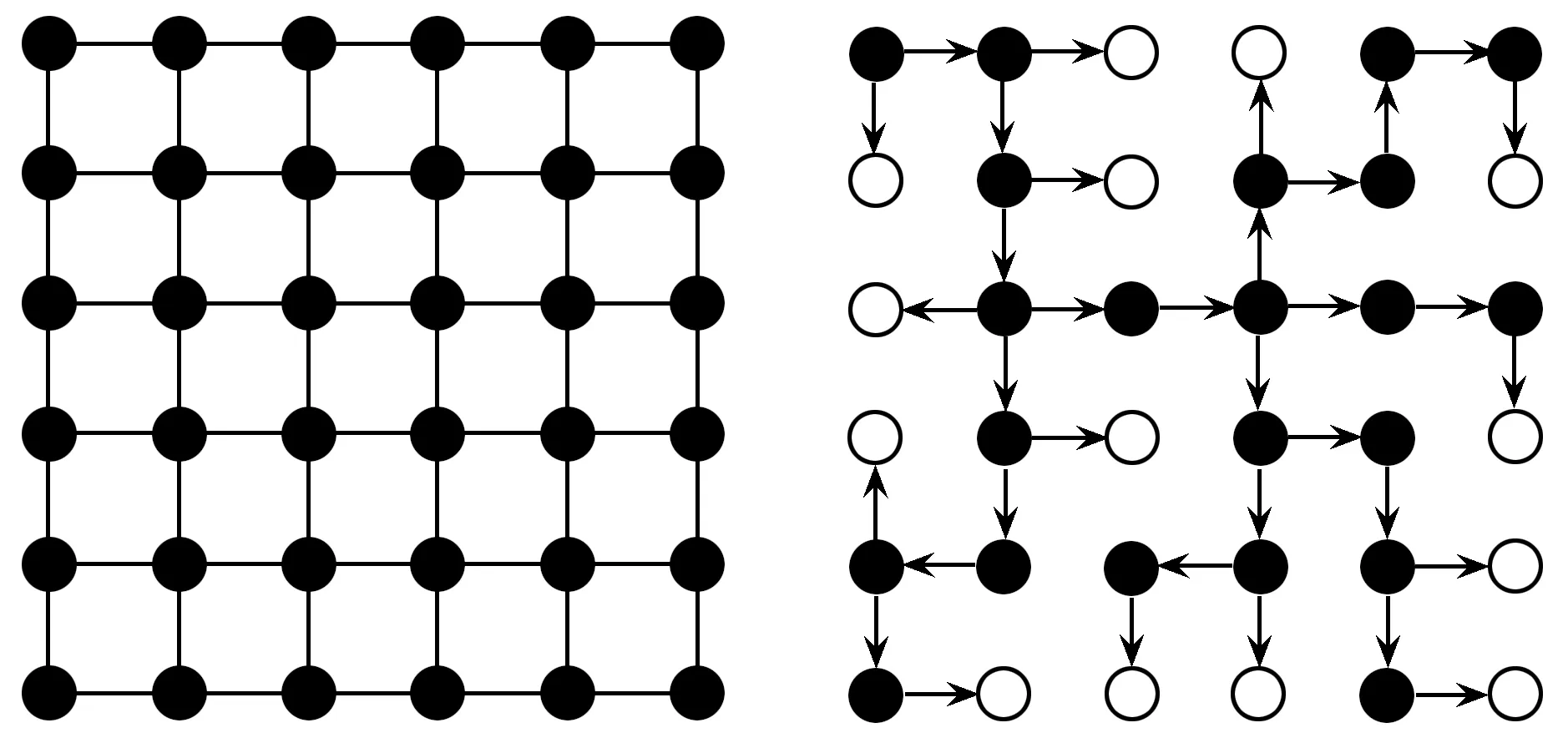
图1 最小生成树图

去掉那些权重较大的边，使一幅图串联权重最小，这就是图像的最小生成树，如图1所示，左图表示原始图，右图表示最小生成树图。

在图1中，左图每个像素都与它周围像素相连接，右图根据克鲁斯卡尔算法，按照权值由小到大的次序选取，若选边后不形成回路，则保留作为一条边，若形成回路则除去。图中箭头表示选取的路径，环形表示叶子节点。

最小生成树就是把相似的点连接在一起，通常2个像素在最小生成树中步数越近，那么它们越相似。最小生成树中2个节点之间的相似性L(p,q)可以表示为:

(3)

其中，D(p,q)=D(q,p)表示p、q之间的在最小生成树中的距离，σ为一个常数定值，用于控制L(p,q)大小。

(4)

其中，∑q表示所有点与p点匹配代价总和。

如果每个像素都要计算一遍聚合代价，那这个算法是很复杂的，最小生成树的立体匹配算法其实只需要遍历2次就可以知道每个点的聚合代价。图2左图为以v6为根节点，从叶子到根节点，记录下每个节点中间聚合代价，在聚合代价中用向上的箭头表示中间聚合代价，根据图2可知叶子节点v3中间聚合代价为自己本身，v5中间聚合代价为：

(5)

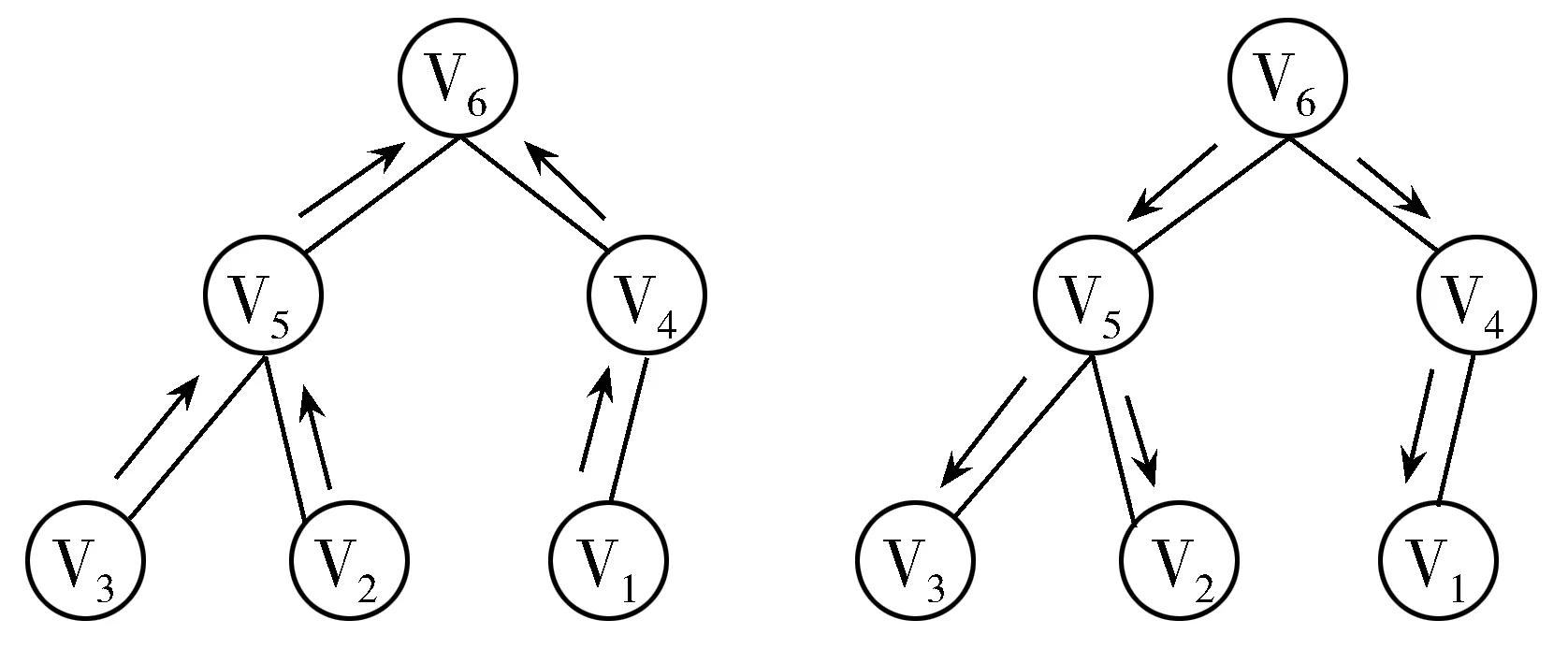
图2 最小生成树遍历图

(6)

图2右图为从根到叶子节点遍历一次。原来根节点是v6,这里定义新的根节点为v5，可以根据之前得到原来根节点的聚合代价得到新的根节点聚合代价,新根节点聚合代价可以表示为：

(7)

因此其他各点的最终聚合代价可以表示为：

(8)

1.3 视差求精

(9)

新的代价值中不稳定的点全为0，它的最终聚合代价全由稳定点提供，最终视差值从稳定点扩散至不稳定点。

为了更好地说明改进匹配方法与MST效果，本文用2种方法对比Middlebury数据集中Baby3图，图3(a)为改进的成本匹配算法，图3(b)为MST最小生成树算法，图3(c) 为原图和真实视差。

(a) 改进匹配成本 (b) MST (c) 真实视差图3 改进算法和MST对比图

图3中，(a)图中的线框里匹配正确，(b)图中的线框里有一部分未匹配出深度，(c)图为Baby3部分原图和真实视差图，从图中可以看出改进的匹配成本能够降低视差误匹配。

2 加权中值滤波

本章介绍中值滤波和加权中值滤波算法，然后比较加权中值滤波对视差图的改善效果。

2.1 中值滤波

中值滤波[13]是一种非线性的图像平滑方法，它能够很好地滤除脉冲噪声，同时又能够保护目标图像边缘。中值滤波把邻域中的像素按照灰度值进行排序，然后选择该组的中间值作为输出像素值，中值滤波可以定义为：

g(x,y)=median{f(x-i,y-j)} (i,j)∈W

(10)

式(10)中，g(x,y)和f(x-i,y-j)分别为输出和输入像素灰度值，W为模板窗口。

2.2 加权中值滤波

视差图本身就有误匹配，在视差图上做中值滤波虽然能够去掉一些噪点，但也会导致物体边缘轮廓不清晰。为了解决这个问题，引入了加权中值滤波[14]。加权中值滤波给视差图每个像素点加一个权重，这个权重由原图得到。加权中值滤波不仅能够除去噪声，也能够根据原图矫正物体的边缘。加权中值滤波表达式可定义为：

g(x,y)=median{f(x′,y′)w(x′,y′)}

(11)

式(11)中，g(x,y)为加权中值滤波值。f(x′,y′)为输入像素灰度值，w(x′,y′)为原始图像像素的权重值，(x′,y′)是以(x,y)为中心的窗口像素。

在Middlebury数据集中，Aloe是一盆花卉，它能够很好地说明加权中值滤波与中值滤波的差异。图4中，(a)图的线框里放大图的花卉的边缘要比(b)图的更平滑，(c)图为Aloe部分原图和真实视差图。可看出使用加权中值滤波的图像边缘更加接近真实视差。

(a) 加权中值滤波 (b) 中值滤波 (c) 真实视差图4 加权中值滤波和中值滤波对比图

3 实验结果与分析

本文的测试平台为：PC机，3.60 GHz AMD FX-8150，8 GB内存，Visual Studio 2013。实验数据来自于2003、部分2007 的Middlebury数据集和KITTI2015数据集，该数据集包含Tsukuba、Venus、Teddy、Cones、Aloe、Art、Baby1、Baby2、Baby3、Books、Cloth2、Cloth3、Dolls和4张户外街道图。首先，对算法进行定量分析，比较MST和本文算法误匹配率。其次，比较2种算法的平均运行时间。最后，对数据集进行定性的比较，给出4张经典的Middlebury和4张KITTI的效果对比图。

由表1可知本文算法在Tsukuba、Venus、Teddy、Cones、Aloe、Baby1、Baby3、Cloth2、Cloth3中误匹配更低，在Art、Baby2、books、Dolls中MST误匹配率低。MST平均误匹配率为7.20%，改进的MST平均误匹配率为6.93%，因此改进的MST能够降低误匹配。

表1 图像误匹配率 单位：%

2种算法在Middlebury数据集上对每幅图片的平均运行时间如表2所示，MST平均运行时间为1.04 s,本文算法平均运行时间为1.16 s，由于改进了匹配成本，后处理使用了加权中值滤波，所以整体运行时间要比MST更耗时。

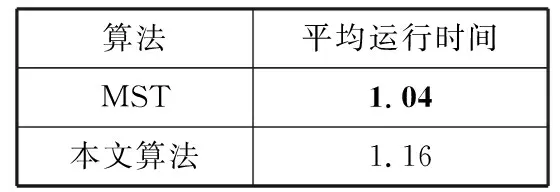
表2 算法平均运行时间 单位：s

进一步分析3种方法在标准的Middlebury的最终视差图，结果如图5所示。在图5中有Tsukuba、Venus、Teddy、Cones这4张经典图，改进的MST在误匹配上要优于MST，目前可以看出加权中值滤波改进MST，在匹配效果图上最好，在边缘和误匹配上都达到最优。

(a) 原图 (b) MST (c) 改进匹配成本 (d) 本文算法

图5 Middlebury效果对比图

室外的场景条件复杂，更具挑战性。利用本文算法对KITTI上的数据进行试验，结果如图6所示。可以看出，MST在室外环境下匹配效果很差。经过加权中值滤波和改进匹配成本处理后，误匹配明显减少，由此可得本文算法在室外环境下比MST更接近真实视差。

(a) 原图 (b) MST (c) 本文算法图6 KITTI效果对比图

4 结束语

本文针对MST图像误匹配和边缘模糊的问题，提出了一种新的基于最小生成树立体匹配成本方法和加权中值滤波方法，旨在提高匹配成本差异和引导图像边缘。实验结果表明，本文算法在Middlebury和KITTI数据集中能够获得很好的匹配效果。新的算法还是无法改善倾斜或者弧度的表面出现波浪式深度，因此下一步工作重点将是研究使用三维坐标表示深度图。

参考文献：

[1] Scharstein D, Szeliski R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J]. International Journal of Computer Vision, 2002,47(1-3):7-42.

[2] Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002,23(11):1222-1239.

[3] Kolmogorov V, Zabih R. What energy functions can be minimized via graph cuts?[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004,26(2):147-159.

[4] Yang Qingxiong, Wang L, Ahuja N. A constant-space belief propagation algorithm for stereo matching[C]// IEEE Conference on Computer Vision and Pattern Recognition. 2010:1458-1465.

[5] Zhang Ke, Lu Jiangbo, Lafruit G. Cross-based local stereo matching using orthogonal integral images[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2009,19(7):1073-1079.

[6] Yoon K J, Kweon I S. Adaptive support-weight approach for correspondence search[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006,28(4):650-656.

[7] Hirschmüller H, Innocent P R, Garibaldi J. Real-time correlation-based stereo vision with reduced border errors[J]. International Journal of Computer Vision, 2002,47(1-3):229-246.

[8] Yang Qingxiong. A non-local cost aggregation method for stereo matching[C]// IEEE Conference on Computer Vision and Pattern Recognition. 2012:1402-1409.

[9] Ma Ziyang, He Kaiming, Wei Yichen, et al. Constant time weighted median filtering for stereo matching and beyond[C]// IEEE International Conference on Computer Vision. 2013:49-56.

[10] Li Linchen, Yu Xin, Zhang Shunli, et al. 3D cost aggregation with multiple minimum spanning trees for stereo matching[J]. Applied Optics, 2017,56(12):3411-3420.

[11] Bleyer M, Rhemann C, Rother C. PatchMatch stereo-stereo matching with slanted support windows[C]// British Machine Vision Conference. 2011:14.1-14.11.

[12] Hamzah R A, Ibrahim H, Hassan A H A. Stereo matching algorithm based on per pixel difference adjustment, iterative guided filter and graph segmentation[J]. Journal of Visual Communication & Image Representation, 2016,42(1):145-160.

[13] Perreault S, Hebert P. Median filtering in constant time[J]. IEEE Transactions on Image Processing, 2007,16(9):2389-2394.

[14] Rhemann C, Hosni A, Bleyer M, et al. Fast cost-volume filtering for visual correspondence and beyond[C]// IEEE Conference on Computer Vision and Pattern Recognition. 2011:3017-3024.