FlexRay动态段消息调度优化算法

张良玉，王 义，张育贵，刘志超，杨 梅

(1.贵州师范大学物理与电子科学学院,贵州 贵阳 550025; 2.贵州大学大数据与信息工程学院,贵州 贵阳 550025)

0 引 言

随着人们对汽车安全性、舒适性、可靠性的要求越来越高，汽车智能化、自动化、信息化的程度也越来越高。汽车内部ECU的数量迅速增加，需要传输的消息与信号也急剧增加。传统的汽车CAN、LIN总线已经不能满足汽车通信网络的通信需求，而作为公认的新一代高速汽车总线标准[1-3]的具有高带宽、高速率、高容错能力[4]的FlexRay总线，能够满足要求。在FlexRay汽车通信网络中，存在着许多非周期实时任务，这些不确定信息在FlexRay总线的动态段中传输。这些随机消息的调度，在一定程度上决定着FlexRay总线的系统性能。FlexRay动态段采用柔性时分多址(FTDMA)媒体访问机制，该机制增强了总线通信灵活性[5]，但也增加了动态段消息调度的难度和复杂度。

目前，FlexRay动态段的研究，大部分针对提高总线利用率或减少消息最坏响应时间为约束条件，来优化动态段长度与通信周期长度及参数配置。文献[1]考虑每个消息长度，提出分配独立的帧ID分析方法，用帧延迟概率作为性能评估。文献[2]提出一种根据动态消息的重要等级，分配ID的方案，并提出最小化消息最坏响应时间的动态段优化算法。文献[3]对FlexRay动态段调度问题，把信号生成与请求时间考虑进来，提出一种基于预留的调度方法，给出了最小持续时间要求的非线性整数规划(NIP)公式。文献[4]提出K-均值聚类模型与分层聚类模型对消息进行聚类，来减少整个FlexRay通信网络内网络占用量，增加通信安全性。文献[5]考虑动态段长度与消息ID的因素，以最大带宽利用率与最小响应时间为目标，设计了FlexRay动态段长度与帧ID的优化设计模型和求解方法。文献[6]提出了时间触发的调度与事件触发的调度相结合的调度算法，使用SAE规范计算最坏响应时间。文献[7]使用实时中间件数据分布式服务(DDS)的方法，来保证数据的正确传输，并计算了最坏响应时间。文献[8]提出了一种新的FlexRay网络参数优化(NPO)模型，并提出一种分析静态段与动态段帧最坏响应时间的算法。文献[9]考虑了不同长度与不同出现概率的消息共享FlexRay动态段数据帧的情况，基于马尔科夫链模型分析了动态段消息延迟。文献[10]设计一种最小化FlexRay总线操作频率模型，建立一种整数线性规划(ILP)模型求解时隙多路复用优化问题。文献[11]基于静态段的优化之上，综合分析静态段、动态段消息的最坏响应时间，得到最优总线周期长度。文献[12]把动态段长度对总线利用率的影响考虑进来，建立提高总线利用率的动态段消息调度算法模型。文献[13]提出了一种快速确定FlexRay动态段时间长度的近似解析方法。文献[14]提出一种静态段与动态段协同调度的方法，用于提高总线利用率与降低传输延时。基于以上研究，本文提出兼顾总线利用率与最坏响应时间的一种启发式调度优化算法。

1 FlexRay协议

1.1 帧格式

FlexRay动态段帧格式，如图1所示。

图1 FlexRay动态段帧格式

消息帧由帧头、有效负载数据段和帧尾这3部分组成。在FlexRay通信协议中，帧头共占5个字节，动态段有效负载数据段的长度可在0～254个字节之中变化，但数据0与数据1占用的字节也可为消息ID字段，以便过滤、控制动态段消息数据。帧尾只有一个数据字段，即24 bit的帧CRC。

1.2 媒体访问机制

FlexRay总线基于循环通信周期来传输消息，周期计数器从0开始计数到63。FlexRay总线通信周期由基于静态时分多址(TDMA)的静态段、基于灵活时分多址(FTDMA)的动态段、可配置的符号窗口和用于节点计算与时钟同步的网络空闲时间组成。一个通信周期长度单元TBUS由若干个最大时间节拍MT(Macrotick)组成，一个MT的长度为1～6 μs，这里取1 μs。

静态段(Static Segment， SS)由多个长度固定相等的静态时隙(static slot)构成，时隙的长度可以配置，每个时隙对应一个固定的节点，长度为TSS。静态段适合传输时间确定的周期性消息，通信系统内，节点之间分配的帧标识符(即帧ID号)互不相同，具有唯一性与确定性。在FlexRay通信系统中，节点的帧ID号和当前时隙号相等时，才能进行通信。

动态段(Dynamic Segment， DS)由若干个长度不固定的最小时隙构成，最小时隙的数量可以配置，用于传输时间不确定的非周期性消息，长度为TDS。在通信系统中，动态段和静态段一样，每个节点在同一时刻分配一个唯一确定的时隙ID号，但动态段中同一个节点中不同的消息可以分配相同的帧ID[5]。动态段有2个时隙计数器，分别用于辨别不同消息的动态时隙计数器和用于计算每个消息长度的最小时隙计数器。动态段消息只有帧ID与当前动态时隙计数器数值相等时，才能发送。

2 动态段消息总线利用率

动态段最小时隙的个数为Nms(2≤Nms≤7988)[15]，长度为tms(取2MT，即2 μs)，则动态段长度TDS为：

TDS=Nms×tms

(1)

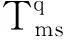
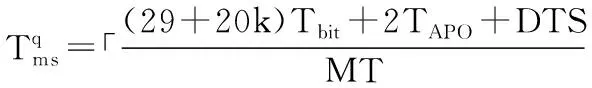
(2)

其中，Tbit等于0.1 μs为一位时间长度；TAPO取1 MT，即1 μs；DTS取4 bit，即0.4 μs。FlexRay动态段消息帧在网络传输时，需要进行编码。根据FlexRay协议中编码规则，每个数据帧要加上最多15 bit的传输起始序列(TSS)、1 bit帧起始序列(FSS)、2 bit字节起始序列(BSS)、2 bit帧结束序列(FES)、11 bit通信空闲分隔符、触发点偏移量(APO)长度为TAPO和2～(tms+2) bit的动态尾部序列(DTS)[12]。

(3)

3 消息最坏响应时间分析

当动态段长度确定时，动态段消息最坏响应时间由帧ID分配方式影响。消息的响应时间影响控制系统的控制性能，其最坏响应时间是系统的重要评价指标。

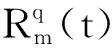
(4)

其中，σm为刚好错过对应的动态时隙而在当前周期内产生的最大延迟[5]；em(t)为节点中相同ID高优先级消息与总线周期内低ID消息造成的整周期最大延迟；Tlast由消息在发送周期中，先发送低ID消息的最长时间；Cm为消息m传输延迟；文献[15]中，TTD和TRD为消息生成延迟与接收延迟共0.2 μs。

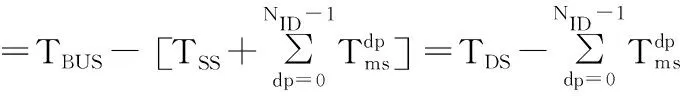
(5)

消息m所在ID队列中高优先级消息集合记为Hp(m,t)，引起延迟周期总数为集合中消息的个数并设为∑Hp(m,t)。总线周期内低ID消息集合记为LID(m,t)，比消息m的ID小，但对应的ID队列为空而未用于传输消息的动态段时隙集合记为Ems(m,t)。由LID(m,t)与Ems(m,t)引起延迟周期总数记为PLE(t)。设LID(m,t)中消息数量为n个，则最多产生n个周期延迟。设二元值变量为xi(i=1,2,…,n)，当xi为1时，第i个周期不能发送消息m，否则xi为0，则PLE(t)为：

(6)

约束条件为：当第i个周期的最小时隙计数器的值j，超过消息mk发送所对应的最小时隙计数器的最大值[5]pLatestTxm(7988个[15])时，xi=1，否则xi=0。对i=1,2,…,n有：

Li>pLatestTxm×tms×xi

(7)

(8)

其中，Li为第i周期的动态段负荷，Lk为消息mk的传输时间。当消息mk在第i个周期第j个动态时隙中发送时，λijk为1，否则为0。所以em(t)为：

em(t)=[∑Hp(m,t)+PLE(t)]×TBUS

(9)

消息m在该传输周期的pLatestTxm时刻被允许发送，产生的延迟Tlast为：

Tlast=TSS+pLatestTxm×tms

(10)

带宽为C，数据线长度为L米，设单位传输延迟0.01 μs/m，帧长度为lmbit的消息传输时延Cm为：

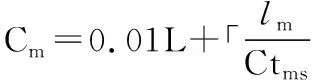
(11)

将式(11)代入式(4)并化简可得：

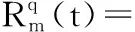
(12)

要满足消息整体可调度，在最坏响应时间下也能在截止时间内发送出去，须满足消息的截止时间不小于最坏响应时间，即：

(13)

动态段整体最坏响应时间Rm(t)为：

(14)

4 消息调度算法

为了建立FlexRay动态段的消息调度算法模型，需要作如下假设：1)所有消息都是非周期性消息，且相互独立；2)所有消息都有固定的长度，且长度、优先级等参数都已知[12]，动态段长度已知，通信周期长度已知。

动态段长度、消息长度已知时，帧ID与消息优先级的分配是影响动态段消息的响应时间以及动态段的网络利用率的决定性因素。优化算法以最大网络利用率与最小响应时间η为目标，η值越小说明网络利用率越大且总体响应时间越小，可利用式(15)计算η：

(15)

(16)

(17)

然后重复执行直到η值经过5次循环不变，则循环结束，输出优化结果。整个算法流程如图2所示。

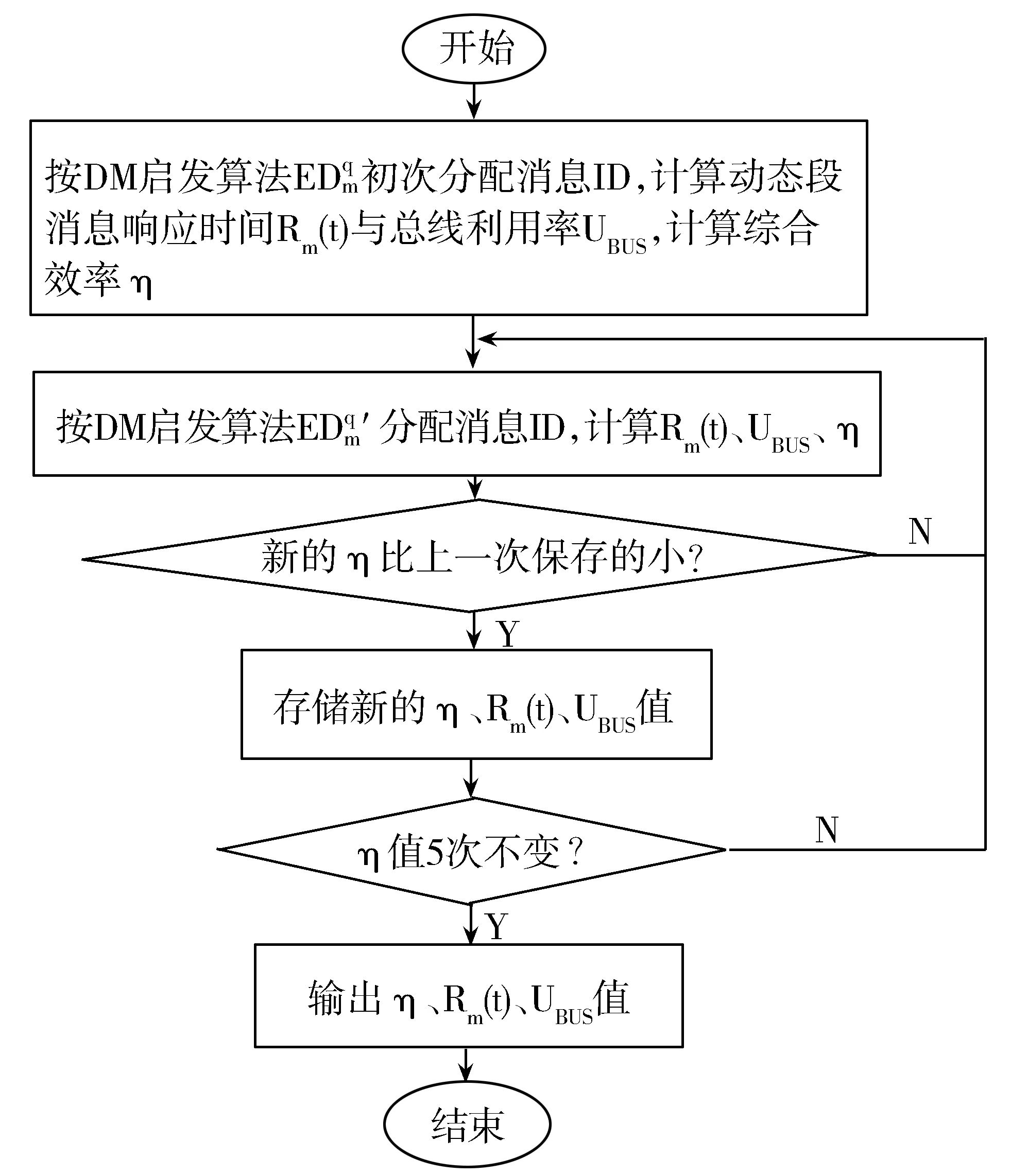
图2 调度算法流程图

5 实验仿真

在Matlab仿真实验中，取文献[5]中的FlexRay动态段消息数据见表1，并参考其设置取动态段长度为1600 μs、静态段长度为2000 μs进行实验。

表1 FlexRay动态段消息

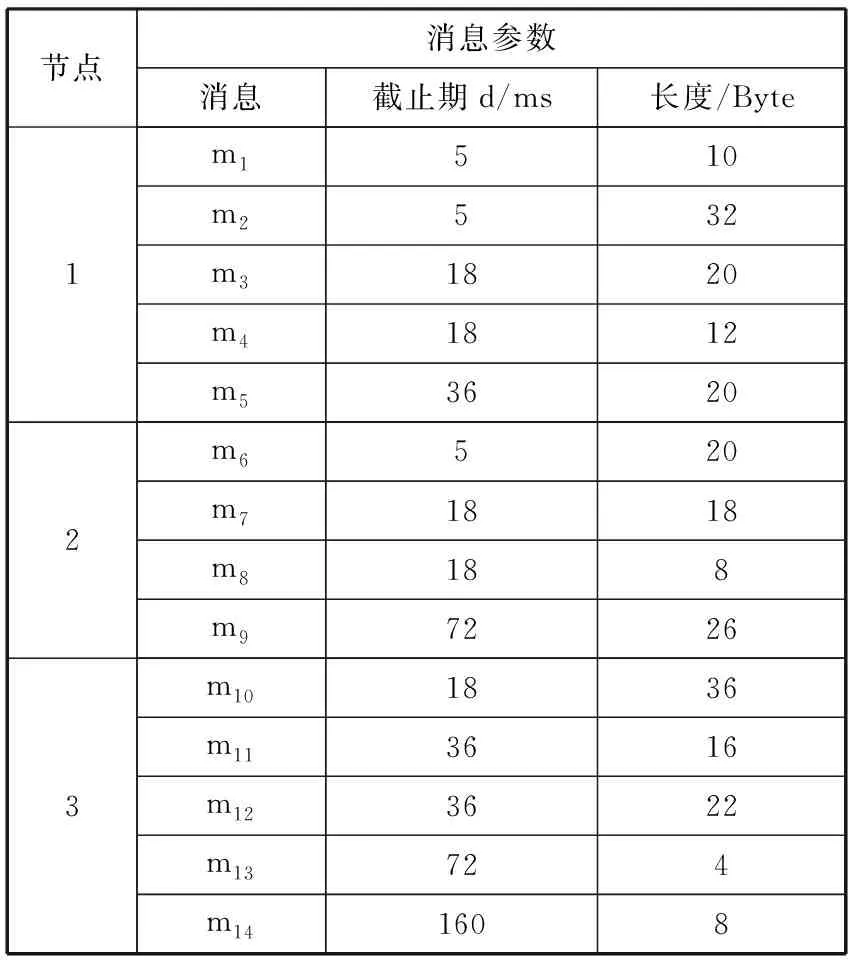
节点消息参数消息截止期d/ms长度/Byte1m1510m2532m31820m41812m536202m6520m71818m8188m972263m101836m113616m123622m13724m141608

FlexRay总线带宽分别在2.5 M和10 M时，本算法优化后的帧ID分配结果如表2所示。实验结果表明不同的速率，帧ID分配结果不完全相同，消息通信性能指标会发生变化。

表2 优化后帧ID分配结果

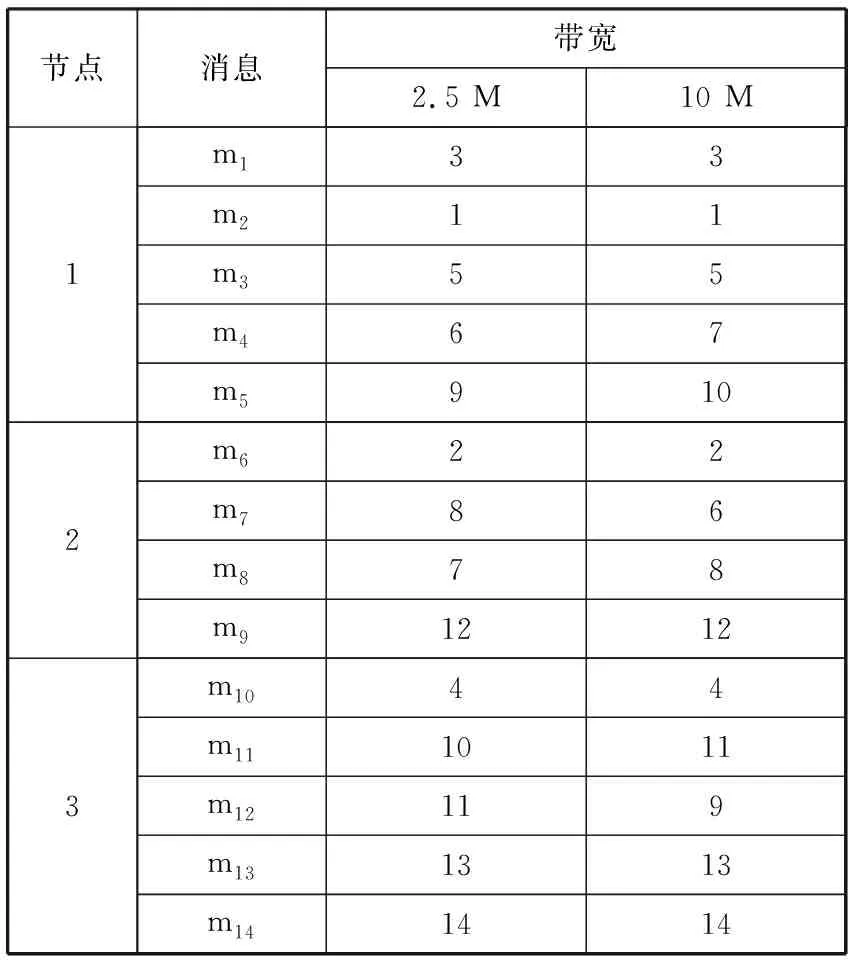
节点消息带宽2.5 M10 M1m133m211m355m467m59102m622m786m878m912123m1044m111011m12119m131313m141414

与文献[5]中的总线利用率对比如表3所示，在带宽为2.5 M与10 M时总线利用率分别提高26.67%与36.76%，验证了本文提出的动态段调度优化算法的有效性。

表3 动态段总线利用率对照表

总线速率/(Mbit·s-1)2.510文献[5]算法计算的动态段总线利用率0.2700.068本文算法计算的动态段总线利用率0.3420.093提高率/%26.6736.76

在带宽为2.5 M时，本文与文献[5]的最坏响应时间对比与按照公式(15)计算的综合效率对比情况如表4所示，分别降低了50.25%与60.37%。

表4 总线利用率对照表

FlexRay总线速率2.5 M文献[5]算法本文算法提高率/%动态段最坏响应时间/ms20110150.25综合效率η744.44295.0160.37

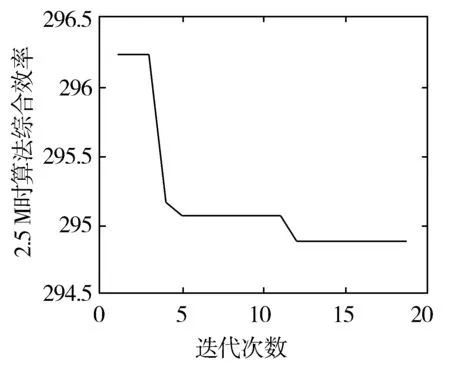
图3 2.5 M时综合效率优化结果

总线带宽分别在2.5 M和10 M时，算法的综合效率如图3、图4所示。

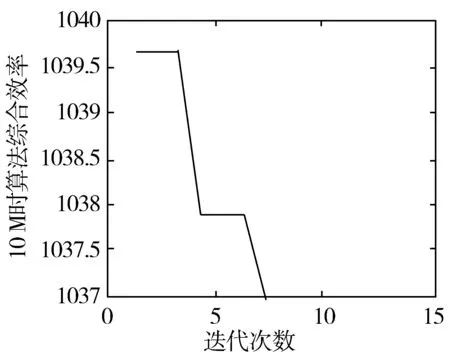
图4 10 M时综合效率优化结果

文献[5]算法模型的不足之处：1)建立在动态段消息最小公倍数的基础上，来计算最坏响应时间，并对非周期消息做周期化，可能增加消息响应时间；2)第4章建立的优化目标函数中最坏响应时间与总线利用率的系数如何选取，存在不确定性，可能使优化结果进入局部最优。本文算法，在通信周期与动态段长度已知的情况下，研究帧ID的不同分配对消息最坏响应时间与总线利用率的综合影响，给出了具体的数学模型，没有不确定参数的选取，但是相比文献[5]，没有对动态段长度进行优化，是本文算法的不足之处。通过上述实验结果，说明本文算法是有效的。

6 结束语

本文从综合总线利用率与最坏响应时间的角度出发，针对FlexRay动态段消息通信特点，在研究了总线利用率与最坏响应时间的计算方法之上，设计FlexRay动态段消息帧ID分配优化算法。该优化算法是一种类DM启发式调度算法，既考虑了消息的截止时间与最坏响应时间，又包含了总线利用率与消息长度。通过仿真验证，综合效率结果表明该算法能够提高总线利用率并减小最坏响应时间。

参考文献：

[1] Kim B, Park K. Analysis of frame delay probability in the FlexRay dynamic segment[C]// IEEE International Conference on Industrial Informatics. 2008：1519-1522.

[2] Wang Y X，Xu Y H，Xu Yi-nan. Efficient utilization of FlexRay network using parameter optimization method[J]. International Journal of Engineering and Technology， 2016,8(6)：439-443.

[3] Schmidt E G, Schmidt K. Message scheduling for the FlexRay protocol: The dynamic segment[J]. IEEE Transactions on Vehicular Technology, 2009,58(5):2160-2169.

[4] Sheu Yung-hoh， Liou Yao-jhong， Wang Zuo-wen. The message scheduling methods of FlexRay communication network based on the clustering methods[J]. Lecture Notes on Software Engineering， 2014,2(4)：365-370.

[5] 王跃飞，殷健力，张利，等. 基于时间约束的汽车FlexRay网络动态段参数设计[J]. 中国机械工程， 2014,25(15)：2070-2075.

[6] Najjar W, Bouhouch R, Jaouani H, et al. Static and dynamic scheduling for FlexRay network using the combined method[J]. International Journal of Information Technology & Systems, 2012,1(1):16-24.

[7] Bouhouch R, Jaouani H, Ncira A B, et al. DDS on top of FlexRay vehicle networks: Scheduling analysis[J]. International Journal of Computer Science and Artificial Intelligence, 2013,3(1):10-26.

[8] Park I, Sunwoo M. FlexRay network param-eter optimization method for automotive applications[J]. IEEE Transactions on Industrial Electronics, 2011,58(4):1449-1459.

[9] 韩强，牛德青，李林珊，等. FlexRay总线动态段传输延迟概率模型[J]. 兵工自动化， 2011，3(2)：33-36.

[10] Makoto S, Akihito I. Slot multiplexing optimization for minimizating the operating frequency of a FlexRay bus under hard real-time constraints[J]. Journal of Information Processing, 2013,21(3):563-571.

[11] 李斌，龙飞. 一种FlexRay总线优化方法研究[J]. 计算机应用与软件， 2015，32(5):141-144.

[12] 王涛. 汽车FlexRay总线动态段时长及消息窗口优化[J]. 汽车科技， 2012(5)：50-54.

[13] 王刚，丁天宝，荣健，等. FlexRay网络的动态段时间优化解析方法[J]. 计算机工程， 2012,38(10)：241-243.

[14] Hua Yu, Rao Lei, Liu Xue, et al. Cooperative and efficient real-time scheduling for automotive communications[C]// IEEE 34th International Conference on Distributed Computing Systems. 2014:134-143.

[15] FlexRay Consortium. FlexRay Communications System Protocol Specification, Version3.0.1[M/OL]. https://svn.ipd.kit.edu/nlrp/public/FlexRay/FlexRay%E2%84%A2%20Protocol%20Specification%20Version%203.0.1.pdf, 2017-06-20.