基于模糊推理的构件度量
陈 晓,孙英昊,赵 攀,刘 倩
(中汇信息技术(上海)有限公司,上海 201203)
0 引 言
基于构件的软件开发是解决软件危机的一种重要手段。通过构件的不断复用和开发,软件生产过程由传统的代码组合转变为构件的模块化组合,将大大提高软件开发的效率和质量。构件作为这种开发模式的核心内容,其质量直接影响构件库和软件开发的质量。因此,构件度量是基于构件的软件开发实践的重要工作。
目前,学者们已广泛开展了构件质量度量方法的研究,并取得了诸多成果。文献[1-2]主要研究构件的复用性,文献[3-6]主要研究构件的可信性。这些研究主要侧重构件的外部质量,缺少考虑构件内部质量的度量,然而,构件内部质量往往直接影响构件的外部质量。文献[7-8]研究了构件的内部质量,但主要研究构件的内聚性,缺少对内部质量的多维度量。文献[9-10]通过静态度量构件的代码,从多个维度度量构件的内部质量,但是没有综合处理量化结果,这导致在软件开发实践过程中,仍需要专家根据各维度的度量结果,人工判断构件内部质量是否达到加入构件库的标准,构件度量效率低。
为解决目前构件度量效率低,并且缺少综合评价构件内部质量的方法等问题,本文提出一种基于模糊推理的构件内部质量度量方法。该方法首先对各个维度的度量结果进行模糊化处理,然后结合由多个专家意见形成的规则库进行规则匹配和结论推理,最后通过逆模糊化输出明确的综合度量的数值结果,从而实现构件内部质量综合度量的自动化。该方法能够汇总多个专家意见,允许使用模糊的不确定信息建立模型,如简单、一般和复杂,使规则库中的规则更接近专家的真实表达,提高规则的准确度。同时,该方法能够模拟专家的推理过程,自动化输出综合考虑多个度量维度的度量结果,节约评审构件内部质量的时间和劳动力,提高工作效率,有利于构件的自动化管理。
1 相关工作
1.1 外部质量度量
目前,学者们主要针对构件的可信性和可复用性等外部质量展开研究。文献[11]根据不同的领域需求选择不同的构件度量模型。文献[12]先通过特征自动机从构件中获得构件的特征点,然后使用加权平均的方法量化了构件的外部质量。基于ISO/IEC 25010[13]软件质量模型,文献[14]使用模糊物元评价法对构件的外部质量进行综合评估,文献[4]针对特定领域的构件,根据构件特点和领域特点来度量构件的可信性。文献[1]基于构件库管理系统,使用构件的复用和检索次数的比值来评价构件的复用性。文献[2]主要通过用户手册、测试报告、运行报告和评价报告等对构件进行外部度量来评价构件的复用性。文献[3]提出了一种基于置信度模型对构件的可信度进行评价。文献[5]考虑不同用户对构件差异性的需求,先对构件度量的各个维度进行主观赋值和权重分配,然后通过执行模糊变换操作对构件的可信质量进行评判。文献[15]指出,构件库中构件之间的依赖关系,可以被用来度量构件的可信程度。构件被使用的次数越多,越值得被信赖。文献[6]基于这种构件之间的依赖关系,对构件进行可信性度量。上述研究工作主要针对构件的外部质量,如复用性和可信性,没有涉及构件内部质量的研究。然而,构件的内部质量往往直接影响构件的外部质量,是决定构件质量的重要组成部分。
1.2 内部质量度量
文献[7]通过提取实现类的依赖图,使用信息熵的计算方法对构件的内聚耦合性进行评价。文献[8]基于程序切片的依赖图方法对构件内聚性进行度量,根据程序的语义衡量构件的内聚性。上述研究工作只对构件的内聚性进行了研究,缺乏对构件内部质量的综合分析。文献[9-10]使用代码静态度量方法来衡量构件的内部质量,如面向过程的Halstead软件科学的度量方法、McCabe圈计数方法等,面向对象的C&K度量集和MOOD度量集等,但是这些代码静态度量方法仅对代码的多个维度进行独立的量化度量,没有根据多个维度的度量结果综合评定构件的内部质量。
在构件快速迭代演化过程中,往往需要避免片面地根据某个维度的度量结果而拒绝构件进入后续的评审工作,从而对构件的内部质量进行综合评定,这将有利于公司循序渐进地提高构件开发水平。同时,上述这些研究虽然能够对构件内部质量进行多维度的量化度量,但是技术开发人员对度量结果的理解却往往具有不确定性,从而导致构件内部质量的度量工作依然需要多位专家参与,这增加了评审构件质量的时间和劳动力,降低了工作效率。
2 影响构件内部质量因素分析
构件的缺陷是构件内部质量的直接反映,内部质量高的构件,缺陷相对较少,修复缺陷所需花费的成本也较低,反之亦然。在团队能力差不多的情况下,可以使用缺陷修复成本综合反映构件的内部质量。
首先,结合圈复杂性度量和C&K度量集指标,将相关度量指标分为复杂性、耦合性和代码风格这3类,然后对每个类别进行细化,涉及的度量维度如表1所示。
表1 度量维度介绍
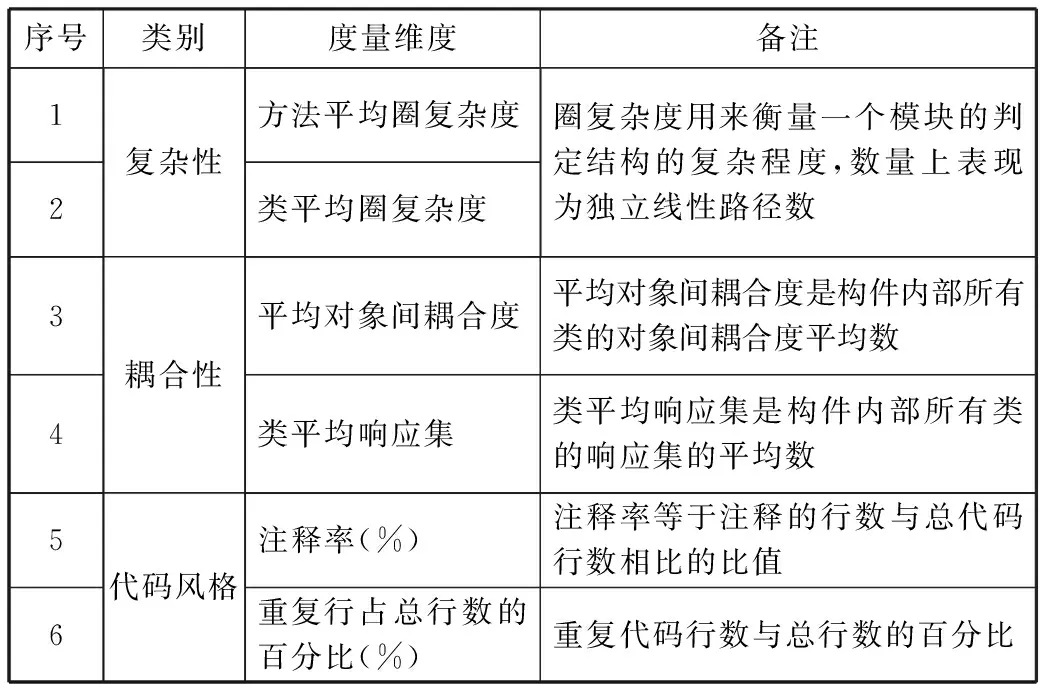
序号类别度量维度备注12复杂性方法平均圈复杂度类平均圈复杂度圈复杂度用来衡量一个模块的判定结构的复杂程度,数量上表现为独立线性路径数34耦合性平均对象间耦合度平均对象间耦合度是构件内部所有类的对象间耦合度平均数类平均响应集类平均响应集是构件内部所有类的响应集的平均数56代码风格注释率(%)注释率等于注释的行数与总代码行数相比的比值重复行占总行数的百分比(%)重复代码行数与总行数的百分比
其次,采用Pearson相关系数d对各度量维度与缺陷修复成本进行相关性计算,其计算公式如式(1):
(1)
其中,a表示各维度通过静态代码分析软件获得的评测值,b表示缺陷修复成本,b可以通过统计缺陷修复的时间来计算。为避免不同规模的构件对相关系数的影响,本文采用每千行代码的构件缺陷修复成本来计算。
然后,采用t分布对d对应的构件样本总体的相关系数ρ进行假设检验。本文假设,H0∶ρ=0,H1∶ρ≠0,检验统计量t的计算公式如式(2):
(2)
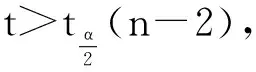
本文选取19个构件样本进行统计,相关性计算结果以及t分布检验结果如表2所示。
表2 度量维度与缺陷修复成本的相关性统计结果
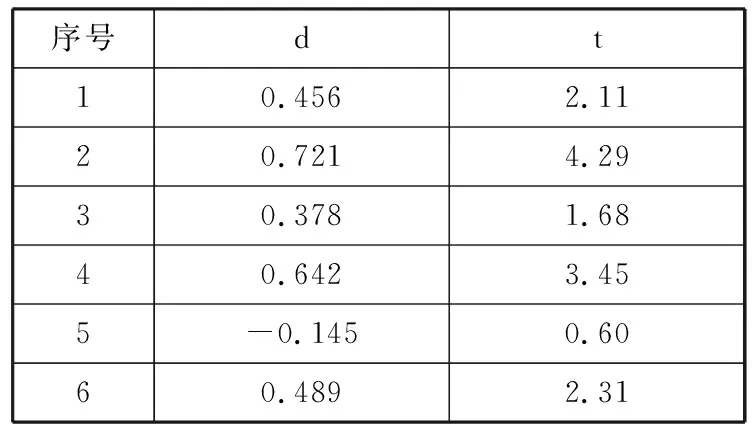
序号dt10.4562.1120.7214.2930.3781.6840.6423.455-0.1450.6060.4892.31
最后,根据上述统计结果,选择最重要的几个维度进行综合度量。根据查表获得的t0.025(17)=2.1098可知,表1中的类平均圈复杂度、类平均响应集和重复行占总行数的百分比这3个指标与缺陷修复成本显著线性相关。因此,选择这3个参数作为构件内部质量的考察维度,即作为模糊推理系统的输入参数。
3 模糊推理系统
虽然类平均圈复杂度、类平均响应集和重复行占总行数的百分比这3个指标对软构件质量有重要影响,但它们间的关系复杂,难以直接建立内部质量的度量模型。因此,本文采用模糊推理的方法,建立质量属性与内部质量的关系模型。
模糊推理是以模糊集合论为基础的描述工具,扩展了以一般集合论为基础的描述工具的数理逻辑。它可根据输入的初始不确定性信息,利用模糊知识中的不确定性知识,按一定的模糊推理策略,较理想地处理待解决的问题,给出恰当的结论[16]。
模糊推理系统包含模糊器、规则库、模糊推理机和逆模糊器4个模块,其结构如图1所示,下面逐一介绍每个模块。
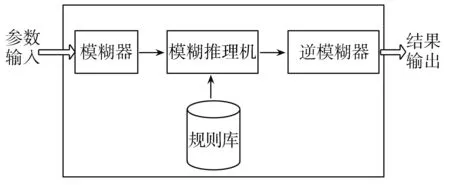
图1 模糊推理系统架构
3.1 模糊器
模糊器将精确输入的数值映射为一个模糊集合,这个过程也称为模糊化处理。输入变量根据其相应的隶属度函数,归到恰当的模糊集合。
本文分别针对上述3个度量维度,以及内部质量进行模糊化处理。考虑到方法步骤的相似性以及篇幅限制,本节以类平均圈复杂度为例详细说明建立输入变量、模糊集及隶属度函数的过程。
本文假设变量x表示类平均圈复杂度,X={S,N,C,VC}表示类平均圈复杂度的模糊集合。其中,子集S表示方法的平均复杂度是简单的集合,N表示一般复杂的集合,C表示较复杂的集合,VC表示非常复杂的集合。根据历史构件统计数据和专家经验,x的取值范围如表3所示。
表3 类的圈平均复杂度变量
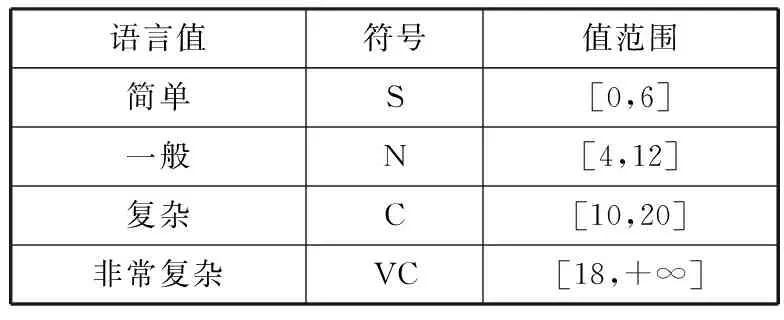
语言值符号值范围简单S[0,6]一般N[4,12]复杂C[10,20]非常复杂VC[18,+∞]
然后,通过专家经验定义类的圈平均复杂度隶属度函数fX(x),如图2所示。
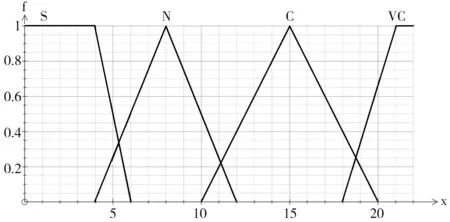
图2 类的圈平均复杂度隶属度函数
使用相同的方法,分别建立类平均响应集的变量y、模糊集合Y和隶属度函数fY(y),如表4和图3所示,以及重复行占总行数的百分比的变量z、模糊集合Z和隶属度函数fZ(z),如表5和图4所示。
表4 类平均响应集变量
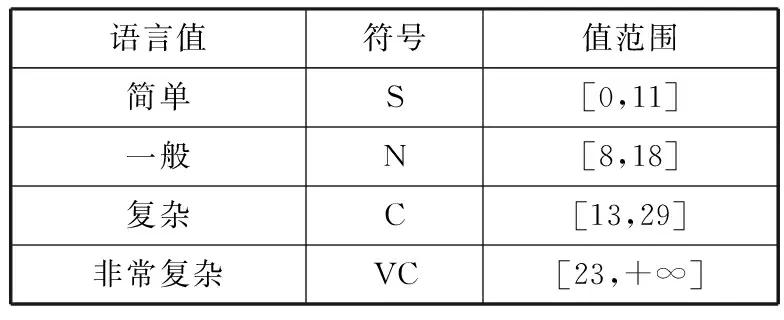
语言值符号值范围简单S[0,11]一般N[8,18]复杂C[13,29]非常复杂VC[23,+∞]
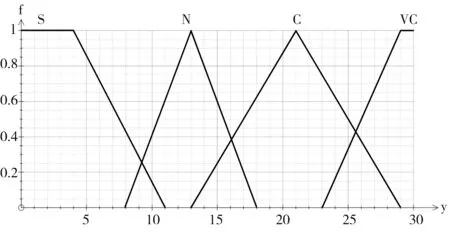
图3 类平均响应集隶属度函数
表5 重复行占总行数的百分比变量

语言值符号值范围很低VL[0,3]低L[2,9]中M[5,15]高H[12,30]非常高VH[20,100]
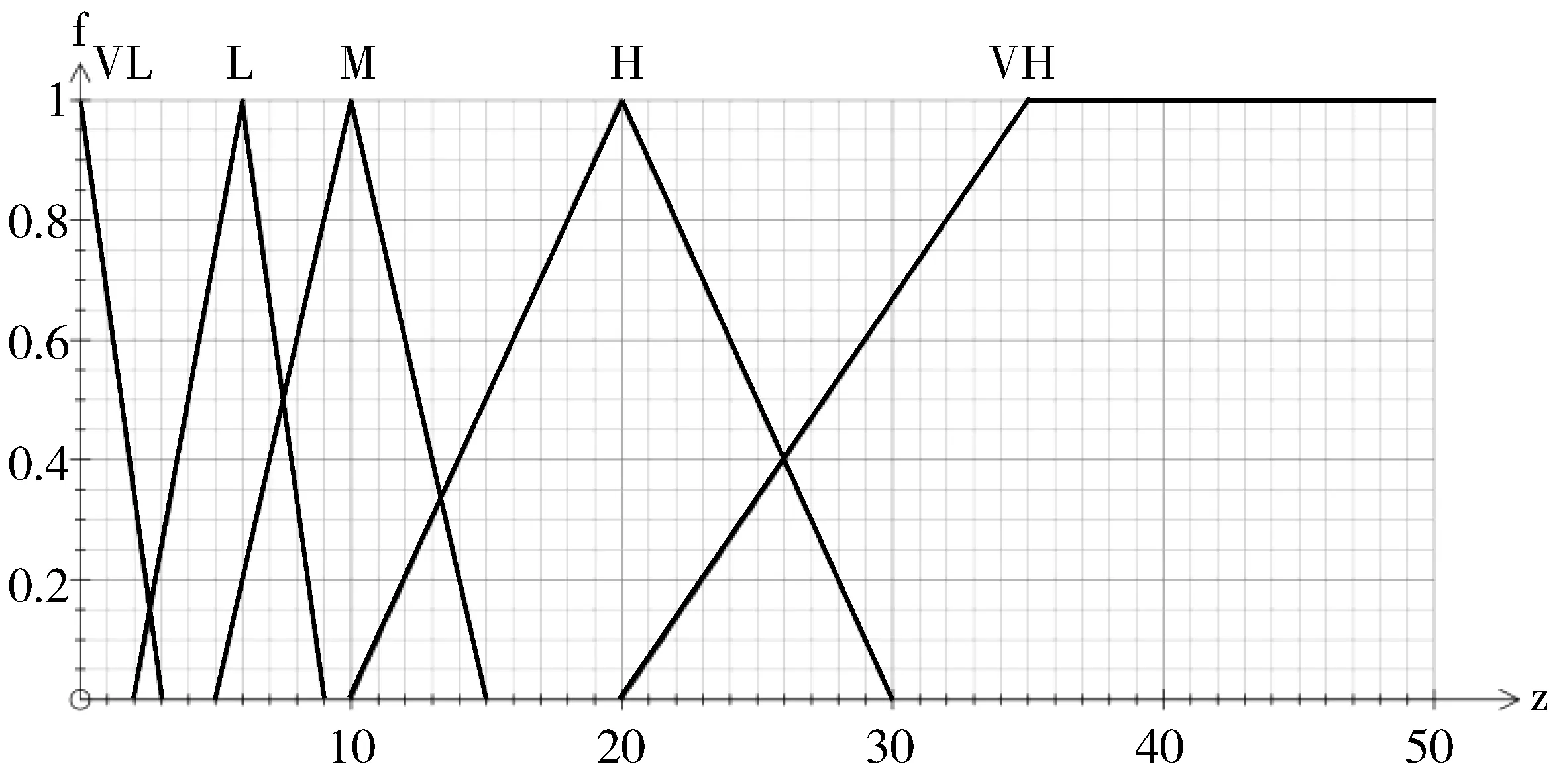
图4 重复行占总行数的百分比的隶属度函数
最后,定义输出变量为构件内部质量w、模糊集合W及其隶属度函数fW(w)。
表6 内部质量程度变量
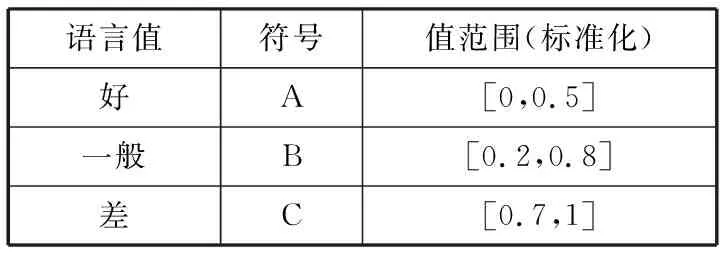
语言值符号值范围(标准化)好A[0,0.5]一般B[0.2,0.8]差C[0.7,1]
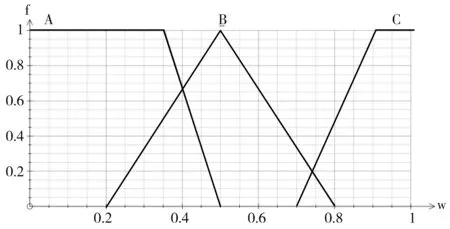
图5 构件内部质量隶属度函数
3.2 规则库
规则库是模糊推理系统的核心部分,它是由一系列产生式规则构成。产生式规则的一般形式为:If x is S then w is B。其中,If对应的部分称为规则的前项,then对应的部分称为规则的后项,x表示输入的考察维度,w表示输出的指标,S和B分别表示相应的模糊集合。对于多输入变量单输出变量的情况,对于由逻辑与组成的规则前项,使用AND相连,如If x is S and y is N then w is B,对于由逻辑或组成的规则前项,使用OR相连,如If x is S or y is N then w is B,其中x和y表示输入维度,S和N表示相应的模糊集合,w表示内部质量,B表示相应的模糊集合[17]。
通过专家经验,建立规则表,如表7所示。其中,规则前项均使用逻辑与(即AND)进行连接。
表7 模糊规则
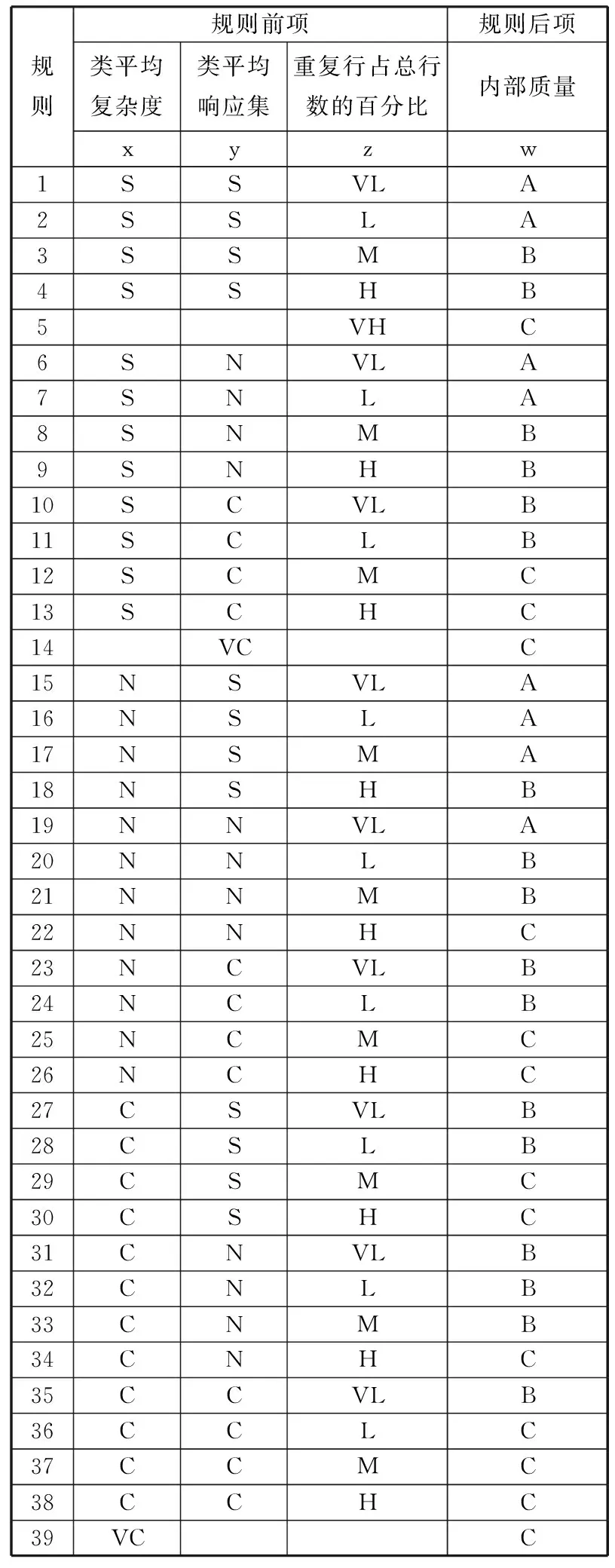
规则规则前项规则后项类平均复杂度类平均响应集重复行占总行数的百分比内部质量xyzw1SSVLA2SSLA3SSMB4SSHB5VHC6SNVLA7SNLA8SNMB9SNHB10SCVLB11SCLB12SCMC13SCHC14VCC15NSVLA16NSLA17NSMA18NSHB19NNVLA20NNLB21NNMB22NNHC23NCVLB24NCLB25NCMC26NCHC27CSVLB28CSLB29CSMC30CSHC31CNVLB32CNLB33CNMB34CNHC35CCVLB36CCLC37CCMC38CCHC39VCC
3.3 模糊推理机
模糊推理机是根据已有的知识规则分析实际情况,再通过逻辑推理,给出结论的过程。本文采用Mamdani模糊推理机模型,在接收模糊化处理的输入结果后,通过规则评估和聚合规则这2个步骤进行模糊推理。
在规则评估中,本文的规则前项均使用逻辑AND进行关联,本文使用min方法进行相应的推理计算,其计算表达式如式(3):
fW(w)=min(fX(x),fY(y),fZ(z))
(3)
该公式表示规则后项的隶属度函数可以通过对规则前项的模糊操作而得到。
聚合规则是整合规则评估中所有激活的规则所获得的规则后项的隶属函数,将它们合并到一个模糊集合中。本文采用最大隶属度原则,使用max方法进行聚合,其计算公式如式(4):
fW(w)=max(fW1(w),fW2(w),…,fWn(w))
(4)
其中,fWn(w)表示第n条规则计算的规则后项隶属度函数。
3.4 逆模糊化器
为获得一个明确的数值作为综合考虑后的度量结果,需要对聚合规则获得的模糊集合进行逆模糊化处理。本文采用质心法进行逆模糊化操作,即寻找一个点,使这个点所在的垂直线能够将聚合集分割成2个相等的部分。计算公式如式(5):
(5)
其中,w*表示内部质量的综合度量结果。
3.5 构件度量样例
首先,对一个构件进行代码静态分析,得到类平均圈复杂度为11.5,类平均响应集为15,重复行占总行数的百分比为10.5。
然后,对各维度的度量结果进行模糊推理,关键步骤的结果如下:
1)由模糊器进行输入值的模糊化处理,得到如下结果,其中括号中的数值表示隶属度函数:
①类平均圈复杂度。
x is N (0.16)
x is C (0.30)
②类平均响应集。
y is N (0.60)
y is C (0.25)
③重复行占总行数的百分比。
z is M (0.90)
z is H (0.05)
2)通过规则引擎,激活规则21、22、24、25、33、34、37、38条规则,经过规则评估分别得到如下结果:
Rule 21:w is B (0.16)
Rule 22:w is C (0.05)
Rule 24:w is C (0.16)
Rule 25:w is C (0.05)
Rule 33:w is B (0.30)
Rule 34:w is C (0.05)
Rule 37:w is C (0.25)
Rule 38:w is C (0.05)
3)聚合如上推理结果,再对模糊集进行逆模糊化处理,得到如图6所示的结果,并输出逆模糊化结果w*=0.63作为内部质量的度量结果。
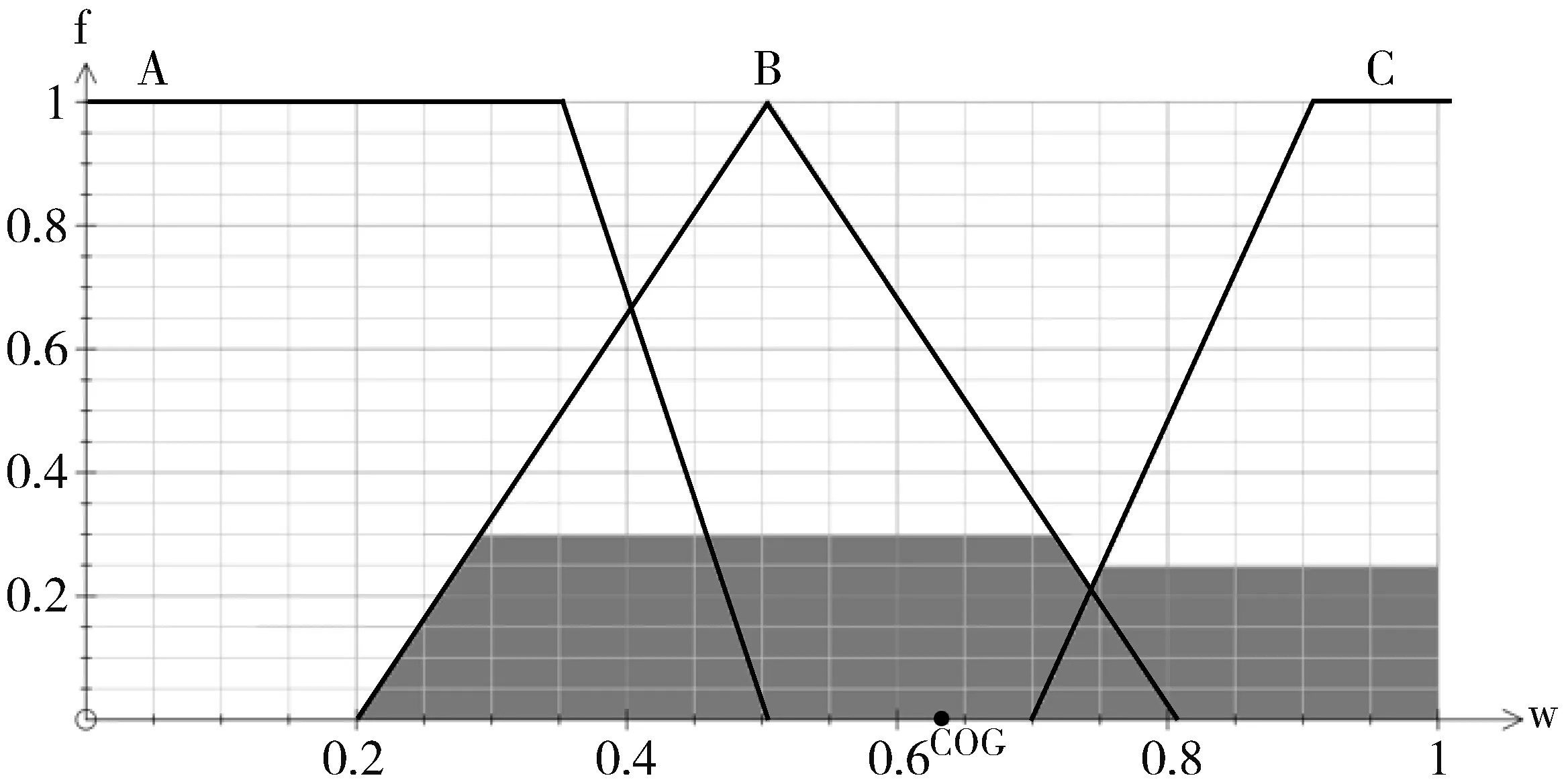
图6 逆模糊化结果
4 实验比较
在实际工作中,软件开发过程随着应用技术的发展逐步演化,演化过程如图7所示。从最初的只包含需求分析、构件开发、应用集成和应用测试的无构件质量评估的开发过程,逐步过度到需要人工专家评估构件质量的开发过程,和基于模糊推理评估构件质量的开发过程。
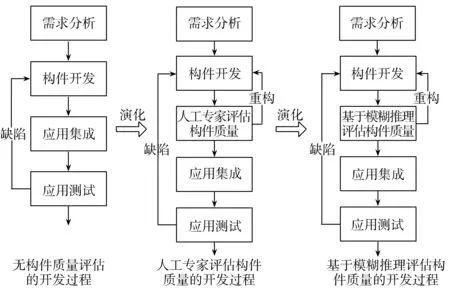
图7 软件开发过程演化
在需要构件质量评估的软件开发过程中,构件需要达到一定标准才能进入应用集成阶段,否则需要进行构件重构,直至满足标准要求。基于模糊推理的构件度量系统能够直接自动化地评估构件质量,从而可在代码的集成过程中完成构件质量评估,方便质量管理人员每天知晓并把控代码质量,及时指导开发人员提高代码质量,进行构件重构。
本文与人工专家评估构件质量的开发过程进行实验对比,对比的指标是平均开发成本,其计算方法是构件完成开发过程的总时长除以千行代码数的平均数值。针对各开发过程中,本文分别随机选取19个构件样本数据,进行平均开发成本的统计计算。本文将人工专家评估质量的开发过程的开发成本作为基数1,实验结果如表8所示。
从表8可以看出,基于模糊推理的构件度量开发模式能够有效降低开发成本。由于本文提出的方法能够自动化地执行,节省了人工审核的时间,因此相较于人工专家评估构件质量的开发模式,本文的方法能够降低开发成本。
表8 构件度量结果对比

平均开发成本/(小时·每千行代码-1)人工专家评估构件质量1基于模糊推理评估构件质量0.83
5 结束语
本文提出了一种基于模糊推理的构件度量方法,能够自动化地综合评价构件的内部质量,为构件入库提供明确的参考依据,减少了人工参与的精力和时间,降低了开发成本,大大提高了构件度量效率。不过,目前还有一些问题需要进一步研究:1)增加内部度量构件质量的考察维度和模糊规则,以提高构件度量的全面性;2)在推理机中引入人工神经网络,实现自动化地产生新的模糊规则,以提高推理机的适应性。
参考文献:
[1] 薛云皎,王渊峰,余枝强,等. 基于构件库管理系统的构件复用度度量模型[J]. 计算机工程与应用, 2002,38(13):81-84.
[2] 李晓丽,刘超,金茂忠,等. 软件构件的可复用性质量度量[J]. 计算机应用研究, 2007,24(6):280-283.
[3] 赵森严,夏琦. 一种基于置信度的软件构件可信性度量模型[J]. 井冈山大学学报(自然科学版), 2013(4):64-66.
[4] 唐莹,张育平,陈海燕. 一种基于特定领域的可信构件度量模型[J]. 计算机与现代化, 2014(10):12-15.
[5] 汪永好,曾广平. 基于模糊集合的构件资源信任评估模型研究[J]. 计算机应用研究, 2014,31(5):1467-1469.
[6] 王燕玲,曾国荪. 基于构件使用依赖关系的构件复用可信度计算方法[J]. 计算机应用, 2015,35(12):3524-3529.
[7] 齐晶晶,郭跟成. 基于信息熵的软件构件度量方法[J]. 计算机应用, 2006,26(5):1183-1185.
[8] 上官盼利,雷航. 构件内聚性度量方法研究[J]. 微计算机信息, 2009(18):190-192.
[9] 梅宏,谢涛. 青鸟构件库的构件度量[J]. 软件学报, 2000,11(5):634-641.
[10] 毛国蓓,李雪静,葛孝堃,等. 基于软件构件质量模型的度量及应用[J]. 计算机应用与软件, 2005,22(5):1-4.
[11] Andreou A S, Tziakouris M. A quality framework for developing and evaluating original software components[J]. Information & Software Technology, 2007,49(2):122-141.
[12] 祁华成,张广泉. 基于特征点的构件度量方法[J]. 苏州大学学报(自然科学版), 2008,24(2):47-51.
[13] ISO/IEC 25010, Systems and Software Engineering Systems and Software Quality Requirements and Evaluation(SQuaRE) —System and Software Quality Models[S].
[14] 汪海涛,刘帅,姜瑛,等. 一种基于模糊物元评价法的构件质量度量模型研究[J]. 云南大学学报(自然科学版), 2015,37(1):31-42.
[15] Ishihara T, Hotta K, Higo Y, et al. Reusing reused code[C]// Proceedings of the 20th Working Conference on Reverse Engineering. 2013:457-461.
[16] 吴钊,尹朝庆. 模糊专家系统推理机设计[J]. 武汉工程大学学报, 2003,25(1):80-82.
[17] Michael N. 人工智能·智能系统指南[M]. 陈薇译.3ed. 北京:机械工业出版社, 2012:56-82.

