基于信息论方法的分类数据相似性度量

郑碧如，吴广潮

(华南理工大学数学学院，广东 广州 510641)

0 引 言

在机器学习算法中，两实例间距离或者相似性度量扮演着重要的角色，广泛地应用于分类、聚类和奇异值检测和特征学习[1-2]等算法中。常用的距离度量方法，如闵可夫斯基距离、马氏距离等，通常只适用于数值型数据。而对于分类数据，其属性为分类属性(如颜色、形状等)，其值具有离散、无序和取值有限的特点，因此，不能直接对2个不同属性值进行比较，通常是利用数据驱动的方法，通过数据的分布情况等信息来对其进行度量。

对已提出的分类数据的度量方法，可分为不相似性和相似性这2大类。不相似性的方法包括Xie等人[3]提出的方法将分类数据映射到实数域，并以此度量不相似性，通过基于最近邻分类错误率最小化来更新值；Cheng等人[4]使用自适应相异矩阵评估分类属性值之间的差异，用梯度下降法优化误差；Le等人[5]则考虑给定2个值与其他属性的条件概率分布差异的组合进行度量，但随数据维度的增大，其复杂度也大大增加。Alamuri等人在文献[6]中介绍了对分类数据的距离或相似性度量的方法，而Boriah等人在文献[2]则侧重介绍了数据驱动的分类数据相似性度量方法，并根据方法所基于的理论对其做如下分类：基于频数的方法有OF(Occurrence Frequency)，IOF(Inverse Occurrence Frequency)，其中IOF与信息检索的逆文档频率的概念相关[7]，Wang等人[8]将其应用到中文文本分析。基于概率的方法有Goodall，Smirnov和Anderberg，其中Goodall提出的度量使得不频繁属性值对整体相似性的贡献大于频繁属性值；而Smirnov不仅考虑给定属性值的概率，还考虑同属性其他取值的概率分布。基于信息论的方法有Burnaby[9]、Lin[10]、Lin1[2]，其中Burnaby提出的方法使得在值不匹配时，对不频繁的属性值赋予较低的相似性；Lin定义2条数据的相似性是其共同的信息与总信息的比率，对频繁值在匹配时赋予更高的权重，对不频繁的值在不匹配时赋予更低的权重；Lin1是Lin相似性的修正方法，其不仅考虑给定属性值的概率，还考虑同属性的概率处于两者间的值的概率。除上面介绍的方法外，还有简单易懂的度量方法：Overlap[11]，其定义2属性值相同时的相似性为1，否则为0；Eskin等人[12]提出的度量是关于属性取值个数的递增函数，取值越多的属性，被赋予更高的权重，但会出现同属性不同值具有同样的相似性。

上述相似性度量方法可应用于分类、聚类算法中，但是在有监督学习任务中，其未利用到数据集的类信息。考虑到类信息对分类有至关重要的作用，本文提出Lin方法改进版本MLin(Modified Lin)，该方法把给定属性值的类概率与信息论方法结合，构造新相似性度量函数，对分类数据进行相似性度量。最后，在UCI机器学习数据库中的多个有类标签的分类数据集上，利用k-NN[13]算法与多个相似性度量方法结合进行实验比较，验证MLin的合理性和效用性。

1 Lin相似性度量

Lin[10]提出的分类数据度量方法是基于信息论的，包括了对有序和无序数据进行相似性度量。本文主要介绍对无序属性的度量方法，Lin认为x和y这2个实例的相似性与它们的共同信息和总描述信息有关。显然，若2实例的共同性越大，相似性越大；差异性越大，相似性越小。

对于2个实例x=(X1,X2,…,Xd)和y=(Y1,Y2,…,Yd)，Lin对其相似性的定义为：

(1)

(2)

(3)

(4)

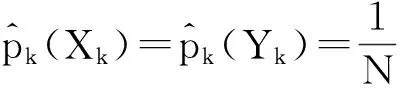
2 Lin相似性度量的改进

2.1 MLin相似性度量

从上一章可知Lin相似性只利用属性值的概率，结合信息论方法构造相似性度量，且2实例的相似性范围为[0,1]。在处理分类问题时，Lin度量没有利用到类标签信息，而类信息对分类起着至关重要的作用。考虑到对带标签数据的相似性度量除利用属性值出现的概率外，还可以利用属性值在各个类上的分布信息，为此，本文将在Lin的理论框架上进行延伸——利用属性值的类条件概率结合信息论方法构造相似性度量，并对该修正方法命名为MLin。

假设分类数据包含C个类别，将Lin相似性中的概率改为类条件概率，即对式(2)～式(4)作如下修正得到式(5)～式(7)：

(5)

(6)

(7)

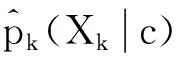
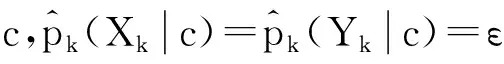
2.2 MLin相似性算法描述与分析

对于MLin相似性，最核心的部分是求出各属性值的类条件概率，再进一步求出属性值间的相似性。在算法1中，先假设属性Ak有nk个取值，再以维度为d，包含C个类别的数据集D作为输入，求出所有属性值的类条件概率列表M,相似度列表S。M的第k个元素Mk是关于Ak的条件概率矩阵，其规模为nk×C；S的第k个元素Sk是关于属性Ak的相似性矩阵，其规模为nk×nk，并且是对称矩阵。

为了方便算法描述，先对数据集进行数据化预处理，把属性Ak的nk个取值按0到nk-1进行标记。例如对颜色(红，黄，蓝)进行如{红：0，黄：1，蓝：2}的形式数字化处理。在此，假设数据集D已经过数值化预处理。

算法1预处理信息提取算法

输入：数据集D={(xi,ci),i=1,2,…,N}，维度d，类别数C

输出：所有属性的类条件概率列表M,属性相似性列表S

过程：

1:初始化类条件概率列表M,属性相似性列表S

2:for k=1,2,…，d do

3:初始化类条件概率矩阵Mk,属性相似性矩阵Sk

4:for i=0,…,nk-1 do

5:for c=1,…,C do

7:end for

8:for j=i,…,nk-1 do

9:Sk[i,j]=Sk(i,j)

10:Sk[j,i]=Sk[i,j]

11:end for

12:end for

13:将Mk,Sk分别加入M,S

14:end for

将算法1的输出类条件概率列表M,属性相似性列表S作为算法2的输入，即可求出2目标实例x,y的相似性。

算法2MLin相似性度量算法

输入：x=(X1,X2,…,Xd)和y=(Y1,Y2,…,Yd)，类条件概率列表M,属性相似性列表S

输出：x和y的相似性S(x,y)

过程：

1:初始化相似度S(x,y)=0,总信息Info=0

2:for k=1,2,…，d do

3:S(x,y)=S(x,y)+Sk[Xk,Yk]

4:for c=1,…,C do

5:Info=Info+log (Mk[Xk,c-1]×Mk[Yk,c-1])

6:end for

7:end for

8:S(x,y)=S(x,y)/Info

3 实验与分析

3.1 数据集描述

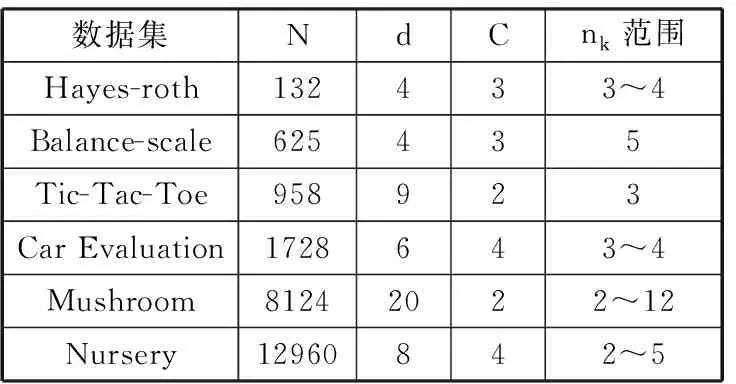
在UCI数据库中选取6个纯分类属性的数据集进行分类，在表1中，给出了各个数据集的名称、数据集包含的实例数N、维度d、类别数C以及各分类属性取值的个数nk范围。

在图1中，图例对图中的折线进行了说明，例如c=1的折线上的各个点为其属性在c=1下的条件概率，各个点的横坐标是其属性值，纵坐标是其所对应的条件概率值。从图1可看出各个数据集在各个类别上属性值的概率分布情况，在Hayes-roth子图中出现3条折线多处重合；在Balance-scale中c=2的折线波动并不大，即c=2的数据对属性值并无明显的偏好；Tic-Tac-Toe和Mushroom都是二分类数据集，其对应子图的折线波动都比较明显；在Car Evaluation上，其在c=1、2时这2条折线在前半部分几乎重合了，c=3、4时也在前半部分出现重合；在Nursery的c=1、3、4上，3条折线的区分度都不大，而c=2的折线波动大，具有较高的区分度。由此可见，对于二分类数据，一般不会出现折线平行或多处点重合的情况。

表1 数据集情况

数据集NdCnk范围Hayes-roth132433～4Balance-scale625435Tic-Tac-Toe958923Car Evaluation1728643～4Mushroom81242022～12Nursery12960842～5

图1 各属性值的类条件概率分布图

3.2 实验结果与分析

把表1中的数据集划分为训练集和测试集，将MLin、Lin、Lin1、Burnaby、IOF、OF、Overlap和Eskin相似性度量方法分别与k-NN[13]结合，通过在训练集中寻找k个与测试集中的目标实例相似度最大的k个实例，并由其类标签进行投票，来预测目标实例所属的类别。由于ID3决策树算法[14]是对离散数据进行分类的经典方法，因此实验中应用ID3对数据集进行分类并与相似度结合k-NN的分类结果作比较。在表2中，给出了各种方法结合k-NN(k=3)在各数据集上进行十折交叉验证的平均错误率。

表2 十折交叉验证的平均错误率(k=3) 单位：%

在表2中，加粗的数值为所在行的最小值，即在某一数据集上的最小分类错误率。从中可看出，ID3在这几个数据集中的判错率都比较低，分类效率高，尤其在数据点较小的Hayes-roth上的平均分类错误率达到最低，体现了其对小数据集具有较好的鲁棒性，在该数据集上，MLin的表现比ID3略差。观察其余多个数据集的分类情况，除了Tic-Tac-Toe在基于IOF的k-NN上的分类效果最好外，其余的4个数据集均在基于MLin的k-NN上的分类错误率最低。尤其在Mushroom上，MLin方法的错误率仅有0.002；并且在Balance-scale上，MLin的准确率比Lin和Lin1的均高出近20%，比ID3高出了近10%的准确率。

图2 k-NN(k=3)十折交叉验证错误率折线图

为了对ID3、MLin、Lin和Lin1的分类结果进行更深入的比较，在k=3时，对其十折交叉验证的错误率画折线图进行可视化，见图2。图中包含6个子图，分别是6个数据集的十折交叉验证错误率折线图，其中横坐标为“avg.”的点的纵坐标值为十折交叉验证的平均错误率。显然可看出Lin1所对应的折线基本处于图的上方，错误率居高，而MLin所在折线几乎都在图的下方，错误率较低。在Hayes-roth的子图中，ID3所在折线明显地处在MLin的下方，这与表2的结论相对应。而在Balance-scale、Car Evaluation和Mushroom这3个子图中，MLin的表现明显优于其他方法。可见，MLin在各数据集的分类具有较高的准确率，ID3的表现处于MLin和Lin之间。综合表2和图2来看，Lin1的综合表现比较差，而MLin的表现都优于Lin，这也验证了MLin在有监督学习分类问题上的度量具有合理性和效用性。

为了比较在不同k值，k-NN方法在各数据集上的分类效果，将数据集分割出30%的数据作为测试集进行测试。在图3中给出了MLin、Lin、Lin1方法在不同k值下k-NN在各数据的测试集上的分类错误率折线图。纵观图3中的6个子图，MLin的错误率的折线几乎都处在图的最下方，而Lin1的分类效果则比较一般。同时可发现，在小数据集上(Hayes-roth，Balance-scale)，MLin的表现比较一般，随着数据集规模的增大，MLin方法下的错误率均较低，如在Nursery数据集上，MLin方法的错误率低于0.05，且明显低于其他方法的错误率。

作为数据驱动的相似性度量方法，并不适合处理小规模数据，若数据集太小，会导致估计的条件概率与实际分布的条件概率有较大的误差。再从时间代价上看，MLin在计算实例的相似度的复杂度比Lin和Lin1相似度方法的复杂度大，再结合k-NN进行分类验证，自然会比ID3花费更多的时间。

4 结束语

本文提出了Lin相似性的改进方法MLin，应用于分类数据的分类问题。MLin是基于信息论和属性值的类条件概率的，将数据的类信息、数据分布考虑入内，属于数据驱动的相似性度量方法。本文中，利用k-NN结合相似性度量方法，对UCI的6个数据集进行实验，结果显示MLin的分类错误率均较低，但在小规模的数据集上的效果比较差，并且也证实了数据驱动方法在小数据集上的表现都会比较差，由此可见MLin更适合应用于数据规模较大的数据中。未来可对其做进一步的扩展和应用，对混合数据进行相似度的度量[15-16]和对文本进行分析[17-18]。

参考文献：

[1] Lin Liang, Wang Guangrun, Zuo Wangmeng, et al. Cross-domain visual matching via generalized similarity measure and feature learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017,39(6):1089-1102.

[2] Boriah S, Chandola V, Kumar V. Similarity measures for categorical data: A comparative evaluation[C]// Proceedings of 2008 SIAM International Conference on Data Mining. 2008:243-254.

[3] Xie Jierui, Szymanski B, Zaki M. Learning dissimilarities for categorical symbols[C]// The 4th Workshop on Feature Selection in Data Mining. 2010:97-106.

[4] Cheng Victor, Li Chun-hung, Kwok J T, et al. Dissimilarity learning for nominal data[J]. Pattern Recognition, 2004,37(7):1471-1477.

[5] Le Siquang, Ho Tubao. An association-based dissimilarity measure for categorical data[J]. Pattern Recognition Letters, 2005,26(16):2549-2557.

[6] Alamuri M, Surampudi B R, Negi A. A survey of distance/similarity measures for categorical data[C]// 2014 IEEE International Joint Conference on Neural Networks. 2014:1907-1914.

[7] Sparck J K. A statistical interpretation of term specificity and its application in retrieval[J]. Journal of Document, 1972,28(1):11-21.

[8] Wang Yue, Ge Jidong, Zhou Yemao, et al. Topic model based text similarity measure for Chinese judgement document[C]// International Conference of Pioneering Computer Scientists, Engineers and Educators. 2017:42-54.

[9] Burnaby T P. On a method for character weighting a similarity coefficient, employing the concept of information[J]. Mathematical Geology, 1970,2(1):25-38.

[10] Lin Dekang. An information-theoretic definition of similarity[C]// Proceedings of the 15th International Conference on Machine Learning. 1998:296-304.

[11] Stanfill C, Waltz D. Toward memory-based reasoning[J]. Communications of the ACM, 1986,29(12):1213-1228.

[12] Eskin E, Arnold A, Prerau M, et al. A geometric framework for unsupervised anomaly detection: Detecting intrusions in unlabeled data[M]// Applications of Data Mining in Computer Security. Springer, Boston, MA, 2002:77-102.

[13] Cover T, Hart P. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory, 1967,13(1):21-27.

[14] Quinlan J R. Induction of decision trees[J]. Machine Learning, 1986,1(1):81-106.

[15] 鞠可一,周德群,吴君民. 混合概念格在案例相似性度量中的应用[J]. 控制与决策, 2010,25(7):987-992.

[16] 赵亮,刘建辉,王星. 基于Hellinger距离的混合数据集中分类变量相似度分析[J]. 计算机科学, 2016,43(6):280-282.

[17] 孙怡帆,李赛. 基于相似度的微博社交网络的社区发现方法[J]. 计算机研究与发展, 2014,51(12):2797-2807.

[18] 陈彦萍,杨威,唐成务,等. 基于语义相似度的数据服务分类方法[J]. 信息技术, 2017(12):93-96.