基于Hadoop的分布式聚类算法研究

吴德超，刘晓红，曲志坚

(山东理工大学 计算机科学与技术学院，山东 淄博 255049)

聚类作为数据挖掘中重要的组成部分，是一种对原始数据进行合理归类的有效方法，然而大批量的数据也给聚类算法的实际应用带来了一些麻烦，比如如何让聚类算法执行的更快速、更有效是当前聚类算法面临的紧迫问题之一.

1 相关研究

1.1 K-means聚类算法的研究

国外对于大数据聚类算法的研究开展较早，研究工作主要集中在为大型数据库的有效和实际聚类分析寻找适当的方法[1].具体研究课题主要集中在聚类方法的可伸缩性、方法对聚类复杂形状和类型的数据的有效性、高维聚类分析技术以及针对大型数据库中混合数值和分类数据的聚类方法.国内在聚类方面的研究较晚，但是研究的进展比较快.杨敏煜提出了一种改进的K-means算法[2]，算法引入权重的思想，考虑到整个数据集，权重能够加速聚类的过程，得到较好的聚类效果.

随着大数据时代的到来，如何提高聚类算法的执行效率对于后续的数据挖掘将起到关键性作用.随着近几年分布式计算模式的兴起，对于聚类算法的执行效率问题给出了一个比较好的解决方案，即利用多台机器并行处理来提高聚类算法处理海量数据的性能.

1.2 Hadoop 计算平台

Hadoop是一个用于并行处理大数据的计算平台，扩容能力强、可靠性好、使用方便.在Hadoop平台上，采用HDFS存储数据、MapReduce编程模式来实现对海量数据的并行化处理[3-4].用户可在不了解底层关系的情况下进行分布式程序开发，快速实现聚类算法的并行化.

1.3 分布式计算的需求

随着计算机技术的不断发展，以往的聚类方式在处理如此大批量的数据时已无法满足人们的需要，近些年分布式技术的发展已经为聚类算法指明了新的方向[5].Hadoop是Apache下开源的一个项目，是一个用于构建云平台的分布式的计算框架. 基于Hadoop计算平台进行聚类任务能够很大程度上降低聚类过程的运行时间，提高计算效率，对解决未来更大规模的数据计算具有重大的意义.

2 算法描述

2.1 K-means 算法优缺点

K-means算法其显著优点是原理简单，容易实现，收敛速度快，因为此K-means算法更适合用于处理大数据.

它也存在一些缺点[6].

(1)K-means算法要求首先要确定K值，现实中很多数据事先不知道包含几类，K值通常是通过经验来确定.

(2)分类结果依赖于分类中心的初始化.

(3)对于离群点数据敏感，离群点对其最终结果影响较大.

2.2 Canopy算法优缺点

Canopy 算法是2000年提出来的[7]，它不会单独用来进行聚类，一般是辅助于其他算法，比如K-means算法，它可以用来确定K值和K个中心点，这样能有效地降低K-means算法中计算点之间距离的复杂度.

Canopy的优点：

(1)Canopy算法用于去除相对较少数据的类簇，这有利于抗干扰.

(2)Canopy选择出来的中心点作为K-means的初始中心点比较合理.

(3)对Canopy算法计算出来的每个类簇进行K-means聚类，能够大幅度减少相似度的计算次数.

Canopy算法缺点：

(1)算法中初始距离T1、T2的确定问题.

(2)Canopy算法执行结束后不能给出较为准确的聚类结果.

Canopy算法不需要事先指定K值，因此可以使用Canopy聚类先对数据进行聚类处理确定K个类簇，然后再使用K-means进行详细聚类得到最终结果.将Canopy算法与K-means算法结合起来不仅能提高精确度，还能很大程度削减计算量.

3 基于Hadoop的K-means+ Canopy 聚类算法

3.1 改进的Canopy算法介绍

Canopy算法的执行结果会受初始阈值T1、T2的影响，当T1较大时，会使同一个点属于多个类簇，增加计算量；当T2过大时，会降低类簇的个数，为了解决T1、T2对于聚类的影响，本文采用“最大最小化原则”来确定T1、T2的值，最大程度提高聚类的准确率.

基于“最大最小化原则”的中心点选择方法的核心思想是：当确定前n个Canopy中心点后，第n+1个Canopy中心点应该选择为所有候选数据点中与前n个中心点之间最小距离的最大者，如公式(1)所示：

(1)

式中DistList代表第n+1个中心点与前n个中心点的最小距离，DistMin(n+1)则表示第n+1个中心点应该为所有最短距离中的最大者.

这种选择中心点的方法在应用中会呈现如下规律：当中心点的个数低于或者大于真实中心点的个数时DistMin(n+1)变化程度较小，当中心点的个数接近真实中心点个数时DistMin(n+1)变化程度较大.为了确定类簇的最优个数以及T1的值，引入深度指标Depth(i)表示变化幅度，其定义如公式(2)：

Depth(k) = |DistMin(k)-DistMin(k-1)| +

|Dist(k+1)-DistMin(k)|

(2)

当k接近真实类簇数时，Depth(k)取得最大值，这时设置T1=DistMin(k)使得结果最优.

3.2 基于Hadoop平台的K-means联合Canopy实现过程

在Hadoop程序开发中最重要的就是MapReduce程序设计与实现，在MapReduce框架下实现K-means + Canopy聚类功能分为Canopy算法代码开发和K-means算法代码开发[8]，其中Canopy算法生成K个类簇，这K个类簇中心可以作为K-means算法的初始聚类中心，K-means算法得到最终的聚类结果，在Hadoop计算框架下每一部分都是分解为多个子任务完成，具体流程如图1所示.

图1 Canopy + K-means算法实现流程Fig.1 Implementation process of Canopy + K-means algorithm

Hadoop平台Canopy算法联合K-means聚类算法的实现步骤如下.

(1)读取数据特征.

(2)执行Canopy算法获取初始聚类中心的步骤：

①将数据的特征矩阵存到一个list中同时基于“最大最小化原则”确定距离阚值T1.

②从list中随机取一个向量P，计算P与所有Canopy之间的距离，如果当前还没有Canopy，则把P作为第一个Canopy，如果P与某个Canopy距离在T1以内，则将点P加入到这个Canopy[9].

③如果向量P与某个Canopy的距离在T2以内，则把P从list中删掉.

④重复步骤2、3，直到list为空结束.

(3)执行K-means算法计算数据对象与聚类中心间的距离，步骤如下：

①选取Canopy算法执行结束后得到的K个簇的中心作为初始聚类中心.

②遍历剩下的所有向量计算其到K个中心的距离，将其归到距离最近的中心点所位于的类簇中.

③对计算得到的K个类簇重新计算每个类簇的中心点.

④再次计算每个点到K个中心点的距离，将其归类到距离最近的那个点所位于的类簇中[10].

⑤重复2到4步，直到中心点位置不再变化或者达到预定的迭代次数为止.

(4)将聚类结果保存.

4 手写数字字形校正

由于个人书写习惯可能会出现字体倾斜的情况，如果对字形进行倾斜校正，会提高聚类准确率[11-12].字形倾斜可以通过计算整体倾斜度来进行校正，目标是使图像的倾斜度尽可能的小，手写数字一般有细长的特点，因此可以将图像的高宽比作为图像倾斜度的依据.在调整图像的倾斜度时引入二分搜索的思想，在倾斜-90°～90°的范围内进行二分查找，寻找最小倾斜角度，使其结果近似最优，具体步骤如下：

(1)因为字体可能左右倾斜，所以设置调整角度的范围在-90°～90°之间.

(2)从手写数字图像中截取数字区域计算图像高宽比，如果高宽比较前一次有所减小，则调整角度减半，继续搜索；如果倾斜度趋于稳定，则退出查找，并使用此时的调整角度对图像进行调整.

图2所示是原图像最终调整55°后的图像对比，明显看出调整后图像中的数字更标准.

图 2 图像调整Fig.2 Image adjustment

5 实验与结果分析

本次实验以开源Hadoop项目作为开发平台,聚类分析对象是手写数字图像.为了比较基于“最大最小化原则”的Canopy算法与传统选取T1、T2值Canopy算法的优劣,在同一数据集下分别采用了以上两种策略进行了对比分析.同时为了比较MapReduce框架处理大批量数据的性能优势,将基于同一数据集与Canopy + K-means 单机算法进行效率对比.另外进行字形倾斜校正，分析字形倾斜对于聚类结果的影响.

5.1 实验环境设置

实验硬件配置为3个服务器节点，每个节点均为8核、8GB内存的PC；软件配置：每个节点均为Linux Ubuntu 14.04操作系统，Hadoop版本为2.6.0，开发包为JDK1.7版本.程序开发工具为 Intellij IDEA，算法由Java实现.

手写数字实验数据来自THE MNIST DATABASE，链接为http://yann.lecun.com/exdb/mnist/.

5.2 实验结果分析

(1)为了验证集群模式与单机模式处理大规模数据时的速度差异，针对同一数据集分别放在两种模式下运行，结果见表1.

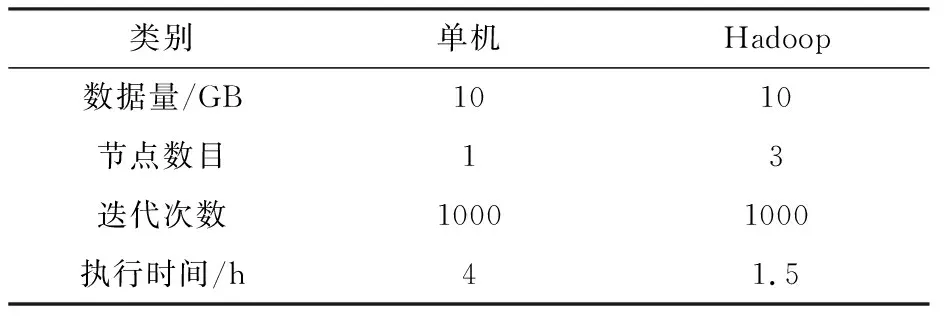
表1 单机模式与Hadoop集群模式对比Tab.1 Execution comparison between standalone mode and Hadoop cluster

从表1中可以看处理Hadoop集群的计算优势非常明显,程序执行时间较单机计算时间缩短.Hadoop集群适用于更大数量级的处理，数量级在TB级别时Hadoop优势更为明显.这里做一个拥有3个节点的Hadoop集群与单机处理不同量级速度的对比，如图3所示.

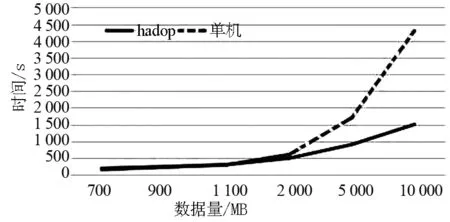
图3 Hadoop集群与单机处理耗时对比Fig.3 Comparison of time between Hadoop cluster and stand- alone processing

从图3可以看出数据量在1 100MB以下时，Hadoop集群与单机计算速度几乎没有差别，甚至数据量在不到900MB时单机计算速度优于Hadoop集群，这是由于在Hadoop集群中会有系统初始化、中间文件生成以及传递等操作，这些操作会消耗一定的时间，所以在数据量较小时Hadoop集群的速度优势体现不出来，但是当数据量达到2GB以上时，Hadoop集群的优势开始凸显，而且这种优势随着数据量的增大愈加明显.

(2)基于“最大最小化原则”的Canopy算法确定初始化中心点与传统确定T1、T2值的Canopy算法确定初始聚类中心比较：

①聚类对象为单个的手写数字图像，有0～9十种数字.

②图像特征基于灰度值提取.

③传统Canopy算法设置T1为数据集中所有元素间的距离的平均值的一半,T2为三倍的T1.

通过传统和“最大最小化原则”两种Canopy算法方式选出初始聚类中心，然后基于Hadoop进行K-means算法聚类，重复执行5次，聚类结果分析见表2.

表2 传统与“最大最小化原则”的Canopy算法准确率对比Tab.2 The accuracy comparison of traditional Canopy algorithm and the one with “maximum minimization principle”

手写数字特征集合大小为10GB，分别通过传统Canopy算法和基于“最大最小化原则”的Canopy算法两种方式选取初始聚类中心点，聚类结束后随机抽取一个类簇的20条数据，计算出正确率.从这5次的结果可以得出随机选取初始聚类中心的聚类结果会因为初始中心点的不同而产生波动，而由于Canopy算法能够有效避免陷入局部最优，所以通过Canopy算法得到初始聚类中心聚类结果较为稳定，准确率也相对较高.

(3)分析字形倾斜对于聚类结果的影响，字形倾斜矫正伪代码如下：

Begin:

maxAngle = 90, minAngle = -90,midAngle

= (maxAngle+minAngle)/2

/*初始化值*/

While minAngle < maxAngle do

height,width = getInfo(img)

rate1 = height / width /*计算比率*/

rotatedImg = rotate(image, midAngle) /*旋转数字*/

new_height, new_width =

getInfo(rotatedImg)

rate2 = new_height / new_width

if rate2 > rate1 then

minAngle=midAngle+1

elseif rate2 < rate1 then

maxAngle=midAngle-1

else exit

midAngle=

(maxAngle+minAngle) / 2

End.

数字倾斜度调整结束后提取图像灰度值作为特征，然后通过传统与“最大最小化原则”两种方式的Canopy算法进行初始聚类中心点选取，聚类结束后随机抽取一个类簇的20条数据，计算出正确率.重复执行5次，结果见表3.

表3 字形调整后传统与“最大最小化原则”的Canopy算法选取初始中心点的准确率对比Tab.3 The accuracy comparison of the initial center point by the traditional and "maximum minimization principle" Canopy algorithm

比较表3和表2可以看出，字形倾斜校正后两种模式的Canopy算法选取初始中心点的准确率明显不同，由于字形调整后字体变得标准和统一，提取出的特征也会相对标准化，才能得出较好的聚类结果.

6 结束语

针对传统Canopy+K-means算法的一些不足，尤其是在处理大数据时面临的效率和准确度问题，提出了基于Hadoop平台上的K-means算法，并且基于“最大最小化原则”对Canopy算法进行优化.另外通过字形调整进一步提高了特征数据的质量.通过以上这些操作大大提高了聚类的准确率及效率.

[1]丁祥武, 郭涛, 王梅,等. 一种大规模分类数据聚类算法及其并行实现[J]. 计算机研究与发展, 2016, 53(5):1 063-1 071.

[2] 杨敏煜. 基于改进聚类算法的数据挖掘系统的研究与实现[D]. 成都：电子科技大学, 2012.

[3]武霞, 董增寿, 孟晓燕. 基于大数据平台HADOOP的聚类算法K值优化研究[J]. 太原科技大学学报, 2015, 36(2):92-96.

[4]SINGH H, BAWA S. A mapreduce-based scalablediscovery and indexing of structured big data[J]. Future Generation Computer Systems, 2017, 73:32-43.

[5]李正兵, 罗斌, 翟素兰,等. 基于关联图划分的KMEANS算法[J]. 计算机工程与应用, 2013, 49(21):141-144.

[6]ABUBAKER M, ASHOUR W. Efficient data clustering algorithms:improvements over kmeans[J]. International Joural OF Intelligent Systems & Applications, 2013, 5(3):37-49.

[7]韩锐, 崔创雄. 一种基于CANOPY算法的聚类优化方法及系统:中国, CN201410194172.7[P]. 2015-11-25.

[8]尹超. 基于HADOOP的聚类算法的研究与应用[D]. 西安：西安建筑科技大学, 2013.

[9]SREEDHAR C, KASIVISWANATH N, REDDY P C. Clustering large datasets using K-Means modified inter and intra clustering (KM-I2C) in hadoop[J]. Journal of Big Data, 2017, 4(1):8-11.

[10]余长俊, 张燃. 云环境下基于CANOPY聚类的FCM算法研究[J]. 计算机科学, 2014, 41(S2):316-319.

[11]王崇阳, 傅迎华, 陈玮,等. 一种改进的稀疏表示的手写数字识别[J]. 信息技术, 2015(2):5-8.

[12]YANG X, LIU W, TAO D, et al. Canonical correlation analysis networks for two -view image recognition [J]. Information Sciences, 2017, 385(C):338-352.