平面向量的创新题赏析

■吴琳琳

平面向量作为高考的必考内容，一直受到命题者的青睐，尤其是与平面向量有关的多选填空题，值得大家关注。这类问题形式新颖，内容综合，具有一定的创新性与挑战性。让我们赏析几例。

一、新坐标系下的向量运算

例 1如图1，设α∈(0，π)，且当∠x O y=α时，定义平面坐标系x O y为α-仿射坐标系，也称为斜坐标系。

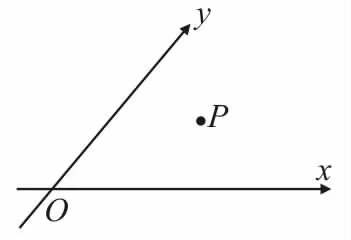
图1

在α-仿射坐标系中，任一点P的斜坐标这样定义:e1，e2分别为与x轴，y轴正向相同的单位向量，若=x e+y e，则记为12=(x，y)，那么在以下的结论中，正确 的是____。(填上所有正确结论的序号)

①设a=(m，n)，b=(s，t)，若a=b，则m=s，n=t；② 设a=(m，n)，则 a =；③设a=(m，n)，b=(s，t)，若a∥b，则m t-n s=0；④设a=(m，n)，b=(s，t)，若a⊥b，则 m s+n t=0；⑤设a=(1，2)，b=

解：显然①正确。由 a =|m e1+n e2|误。由a∥b，可得b=λ a(λ∈R)，所以s=λ m，t=λ n，则 m t-n s=0，③正确。由a·b=(m e1+n e2)·(s e1+t e2)=m s+n t+(m t+n s)cosα≠m s+n t，可知④错误。根据数量积公式a·b=a bcos〈a，b〉，a =，a·b=4+5e1·e2，可得4+=(5+4e·e)·cos，可知12e·e=--12⑤正确。答案为①③⑤。

评注：对于平面直角坐标系来说，若两个单位基向量i与j互相垂直，则i·j=0。对于斜坐标系来说，e1·e2=cosα。它们表面上看似乎不同，其实当α为直角时，斜坐标系就变成了直角坐标系。

二、新定义下的向量运算

例2定义两个平面向量的一种运算:a⊗b=|a|·|b|sin〈a，b〉。现有关于平面向量的上述运算的四个结论:①a⊗b=b⊗a；②λ(a⊗b)=(λ a)⊗b；③若a=λ b，则a⊗b=0；④若a=λ b且λ＞0，则(a+b)⊗c=(a⊗c)+(b⊗c)。其中恒成立的结论是____。(只填写序号)

解：对于①，由向量的模是实数，且实数的乘法运算满足交换律，可知a⊗b=b⊗a成立。对于②，λ(a⊗b)=λ|a|·|b|sin〈a，b〉，(λ a)⊗b=|λ a|·|b|sin〈λ a，b〉，当λ＜0时，λ(a⊗b)=(λ a)⊗b 不成立。对于③，若a=λ b，则sin〈a，b〉=0，故a⊗b=0恒成立。对于④，若a=λ b，则a+b=(1+λ)b，(a+b)⊗c=|(1+λ)b|·|c|sin〈b，c〉，(a⊗c)+(b⊗c)=|λ b|·|c|sin〈b，c〉+|b|·|c|sin〈b，c〉=|(1+λ)b|·|c|sin〈b，c〉，故(a+b)⊗c=(a⊗c)+(b⊗c)恒成立。答案为①③④。

评注：对新定义问题，可按照给定的法则进行运算即可。此类问题虽然给出的信息比较多，其实质却很简单，利用简单的向量运算即可解决。

三、平面向量与三角形“四心”问题

例 3O是平面α上一定点，A，B，C是平面α上△ABC的三个顶点，∠B，∠C分别是边AC，AB对应的角。下列命题正确的序号是 。

评注：当平面向量与三角形的“四心”结合在一起时，更能体现平面向量的几何特征。本题看似复杂，其实只是考查了平面向量的共线定理。

四、平面向量在三角函数中的应用

例 4求cos5°+cos77°+cos149°+cos 221°+cos 293°的值。

解：如图2，在平面坐标系x O y中，作一个正五边形A1A2A3A4A5。

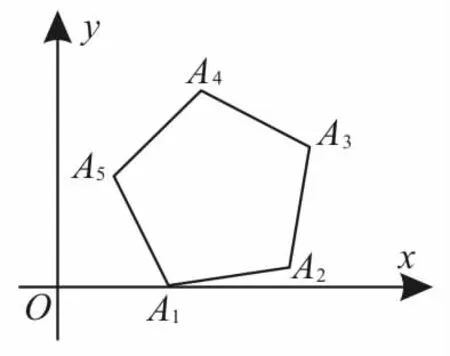
图2

评注：本题将正五边形合理地放置在直角坐标系中，使原本让人无从下手的三角问题转化为容易解决的向量问题。类似的问题有sin5°+sin77°+sin149°+sin221°+sin 293°=0，请同学们证明之。