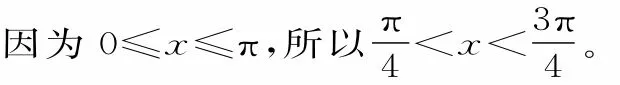本期试卷参考答案与提示

编者的话：同学们在演练的过程中，如果需要更为详细的参考答案，请扫描右边的二维码，关注编辑部的官微“高中数学解题反思”，不但能获悉详细参考答案，还可以另辟蹊径，开拓知识视野，学会解题反思!

平面向量综合演练A卷参考答案与提示

一、选择题

二、填空题

25.926.提示:因为a与b为两个不共线的单位向量，所以|a|=|b|=1。又a+b与k a-b垂直，所以(a+b)·(k a-b)=0，即k a2+k a·b-a·b-b2=0，可得k-1+k a·b-a·b=0，即k-1+kcosθ-cosθ=0(θ为a 与b的夹角)，所以(k-1)(1+cosθ)=0。因为a与b不共线，所以cosθ≠-1，可得k=1。 27.(-6，21) 28.-3

三、解答题

36.提示:由题设知=dc=2b-3a=e-c=t(a+b)-3a=(t-3)a+t b。C，D，E三点共线的充要条件是存在实数k，使得，即(t-3)a+t b=-3k a+2k b，整理得(t-3+3k)a=(2k-t)b。

若a，b共线，则t可为任意实数；若a，b

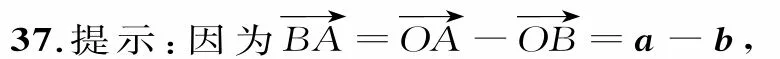
39.提示:(1)因为(2a-3b)·(2a+b)=61，所以4|a|2-4a·b-3|b|2=61。

平面向量综合演练B卷参考答案与提示

一、选择题

二、填空题

三、解答题

36.提示:(1)因为(a-b)·c=a·cb·c=|a|·|c|·cos120°-|b|·|c|·cos 120°=0，所以(a-b)⊥c。

(2)|k a+b+c|＞1⇒|k a+b+c|2＞1⇒k2a2+b2+c2+2k a·b+2k a·c+2b·c＞1。因为|a|=|b|=|c|=1，且a，b，c相互之间的夹角均为120°，所以a2=b2=c2=1，a·b=b·c=a·c=-，可得k2+2-2k-1＞1，即k2-2k＞0，解得k＞2或k＜0。

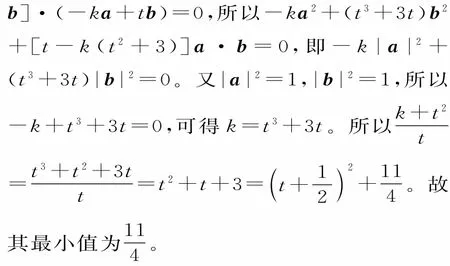
39.提示:(1)设点C的坐标为(x0，y0)。

在平行四边形ABCD中，由+=(3，5)+(6，0)=(9，5)，即(x0-1，y0-1)=(9，5)，得x0=10，y0=6，即点C(10，6)。

(2)由平行四边形ABCD和M 是线段AB的中点，可知点P为三角形ABC的重心，则

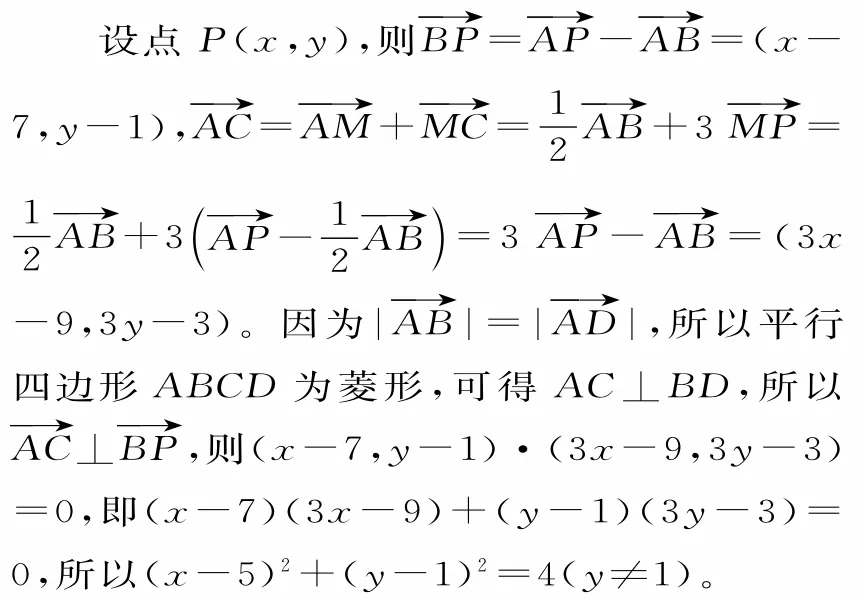
故点P的轨迹是以(5，1)为圆心，2为半径的圆去掉与直线y=1的两个交点。

40.提示:(1)a·b=2sin2x+1，c·d=2cos2x+1。由正、余弦函数的值域可得到1≤a·b≤3，1≤c·d≤3。

(2)由(1)所求得的范围与二次项系数为正的二次函数f(x)的对称轴为x=1，可知函数f(x)在[1，+∞)上单调递增，即不等式f(a·b)＞f(c·d)可转化为a·b＞c·d，即2sin2x+1＞2cos2x+1，所以2(cos2x-sin2x)＜0，可得 (cosx+sinx)·(cosx-sinx)＜0。