平面向量的基本概念及其运算

■王 焓

■王 焓

平面向量既有几何图形的特征，又有代数运算的特性，它是沟通代数与几何的桥梁。高考主要考查平面向量的基本概念与表示、平面向量的线性运算、平面向量的基本定理与坐标表示，以及平面向量的数量积。

1.平面向量的线性运算及基本定理

例 1在下列向量组中，可以把向量a=(3，2)表示出来的是( )。

A.e1=(0，0)，e2=(1，2)

B.e1=(-1，2)，e2=(5，-2)

C.e1=(3，5)，e2=(6，10)

D.e1=(2，-3)，e2=(-2，3)

解：因为e1=(-1，2)，e2=(5，-2)不共线，且a=2e1+e2，故选B。

点拨：两个不共线的非零向量作为一组基底，用它可以将平面内的任何向量都表示出来。

例2设M为平行四边形ABCD对角线的交点，O为平行四边形ABCD所在平面内的任一点，则等于( )。

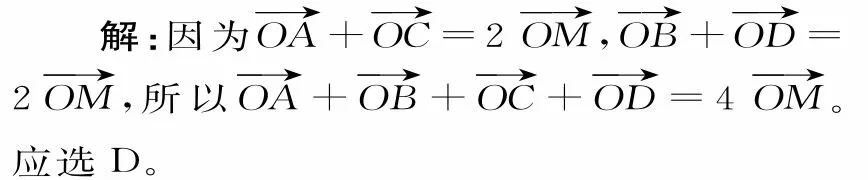
点拨：利用向量加法的三角形法则和平行四边形法则，可以把两个不共线的向量用一个向量来表示。

2.平面向量的平行与垂直

例 3已知向量a=(2，6)，b=(-1，λ)，若向量a∥b，则λ=____。

解：由a∥b，可得-6=2λ，即λ=-3。

例 4设向量a=(3，3)，b=(1，-1)，若(a+λ b)⊥(a-λ b)，则实数λ=____。

解：由题设可得(a+λ b)·(a-λ b)=0，即(3+λ)(3-λ)+(3-λ)(3+λ)=0，解得λ=±3。

点拨：若向量a=(x1，y1)，b=(x2，y2)，则a∥b⇔x1y2-x2y1=0，a⊥b⇔x1x2+y1y2=0。

3.平面向量的模

例 5已知向量a，b的夹角为60°，|a|=2，|b|=1，则|a+2b|=____。

解法1：作两个 向 量=2b，且|a|=2，|b|=1，∠AO B=60°。以O A，O B为两邻边作平行四边形O ACB，此时O ACB是一个相邻两边长均为2且夹角为60°的菱形，则

例 6已知向量a=(cosx，sinx)，b=(3，-)，x∈[0，π]。记f(x)=a·b，求f(x)的最大值和最小值及对应的x的值。

点拨：处理平面向量的数量积的三种常用方法为定义法、基底法和坐标法。

4.平面向量的数量积的应用

点拨：以平面向量为背景，可以考查三角函数的化简、求值及图像与性质等问题。