数学思想在平面向量中的应用

■廖庆伟

平面向量问题中蕴含着丰富的数学思想，在解题时，若能适时地渗透有关的数学思想和方法，则有助于掌握知识技能，提高解题效率。

一、数形结合思想

例 1如图1所示，在△ABC中，点D，F分 别 是 边BC，AC的 中 点

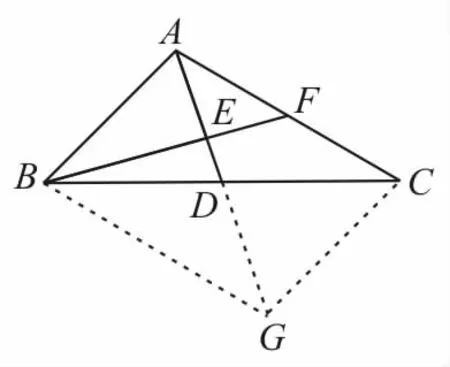
图1

(1)用a，b表示

(2)求证:B，E，F三点共线。

小结：“数无形，少直观，形无数，难入微”。灵活利用向量的“形”的特征，尤其是在解决有关向量的加法、减法问题时，抓住几何特征，可以快速解题。

二、分类讨论思想

例 2如图2，已知平行四边形的三个顶点坐标分别为 A(4，3)，B(3，-1)，C(1，-2)，求第四个顶点D的坐标。

图2

解：设顶点D的坐标为(x，y)。若平行四边形四个顶点的顺序为A，B，C，D，则(1-x，-2-y)。由第四个顶点D的坐标为(2，2)。

综上可知，第四个顶点D的坐标为(2，2)或(6，4)或(0，-6)。

小结：本题主要考查平面向量的坐标运算、平行四边形的性质等知识。

三、化归与转化思想

例 3如图3，在矩形ABCD中，AB=，BC=2，点E为BC的中点，点F在CD上，若的 值 是____。

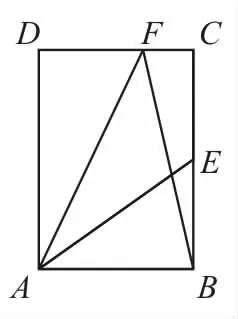
图3

小结：用向量方法解决几何问题的“三步骤”:①用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题；②通过向量运算，研究几何元素之间的关系，如平行、垂直、距离、夹角等问题；③把运算结果“翻译”成几何关系。

四、函数与方程思想

小结：本题主要考查平面向量的数量积运算及二次函数的性质等知识。

例5在平面直角坐标系x O y中，已知向量 a=(-1，2)，点 A(8，0)，B(n，t)，

(1)若⊥a，且||=5||，求。

(2)若与向量a共线，当k＞4且tsinθ取最大值4时，求。

解：(1)由题设知=(n-8，t)。因为⊥a，所以8-n+2t=0。 因 为|=|，所 以5×64=(n-8)2+t2=5t2。 由上解得t=±8。当t=8时，n=24；t=-8时，n=-8。所以=(24，8)或(-8，-8)。

小结：本题主要考查平面向量的坐标运算及正弦函数的性质、二次函数的性质等知识。

五、整体思想

例 6已知非零向量a，b满足|a+b|=|a-b|=2|a|，则向量a+b与a-b的夹角为____。

解：将|a+b|=|a-b|两边平方可得a·b=0，将|a-b|=2|a|两边平方可得b2=3a2。所 以 cos〈a+b，a-b〉=又α∈[0，π]，故向量a+b与a-b的夹角为60°。

小结：本题主要考查向量的夹角的概念，通过整体代入和整体相约，降低了解题的难度。