高三“平面向量的数量积”复习教学反思——探究本源，变中出彩

陈国仙

(江苏省苏州吴江高级中学 215200)

复习课的目的在于“温故而知新”，从旧知识的复习过程中能够发现新内容.随着教学改革的逐渐深入，高三复习课越来越受到数学教师的重视，从中发现学生自身存在的薄弱环节，是对知识进行再次加工的重要手段.笔者从自身的实践体会出发，以高三“平面向量的数量积”复习课为案例，从中产生教学反思，引导学生自主探究，从变中生成教学实录.

一、课堂教学重点难点与反思

1.立足教学目标，掌握重点难点

例1 设非零向量a、b、c满足条件|a|=|b|=|c|，a+b=c，那么向量a和b的夹角为多少度？

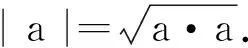
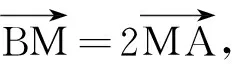
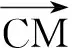
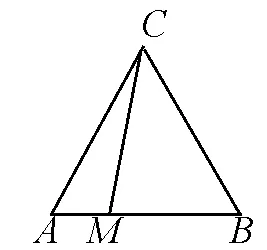
图1

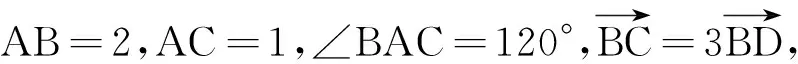
变题2 已知向量a和b的夹角为120°，|a|=1，|b|=3，那么|5a-b|=________.

首先教师从变题2中让学生继续思考以下问题.

变题3 已知 向量a和b的夹角为60°，如果向量ka+b，a-2b的夹角为钝角，求实数k的取值范围.

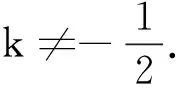
2.课后归纳小结

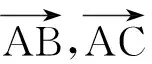
二、对高三数学平面向量的数量积复习课变中出彩的几点反思

首先，教育心理学认为，学生开始思维过程是以问题为基础展开的，从本质上来讲，学习是提出问题，解决问题的过程，每当学生遇到新模块和新知识时，如果已有的经验理论不足以转化为新情境，那么在解决问题的过程中获取到的知识与技能都会形成新的科学解决方法，逐渐形成正确的观点态度.其次变中出彩还是以原始问题为核心，向着蕴涵的各方面进行拓展和深化，揭示出数学概念的本质属性和非本质属性，培养出学生知识情境转化意识和辨别能力意识.

三、结语

综上所述，高三平面向量的数量积变式教学要立足于教材，教师有意识让学生探究出题目本源，从“不变”的本质中探究出“变”的规律，能够帮助学生将所学知识点融会贯通，领悟数学学习的魅力.因此随着新课程改革的逐渐深入，数学教师也要不断更新教学观念，最终提升教学质量和教学效率，并且不断在高三数学复习课中做好教学反思工作.

参考文献：

[1]李小峰.基于题根变式教学的高三一轮复习教学设计——以“平面向量数量积及其应用”为例[J].高中数学教与学,2017(02):36-39.

[2] 赵睿英.利用变式进行板块式教学提高复习效率——高三数学复习课“平面向量的数量积”教学实录[J].上海中学数学,2014(12):9-12.

[3] 程国祥,任为彬.专题复习——平面向量的数量积[J].当代教育实践与教学研究(电子刊),2017(1):145.