利用导数证明函数不等式的五个策略——构、移、放、分、拆

徐加华

(山东省新泰市第一中学 271200)

在近几年的高考和各地的高考模拟试题中，与函数有关的不等式证明问题逐渐受到命题专家的青睐，这类问题具有极强的综合性和技巧性，考查的内容丰富，思想深刻，对于考查考生是否具有扎实的基本功和良好的基本素养不失为一个好的载体.本文立足于当前高中知识，对此类不等式进行了深入的研究.从技巧的角度总结了证明函数不等式的五个策略——构、移、放、分、拆.现结合一些具体例子与大家共享.

一、构

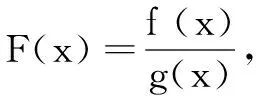
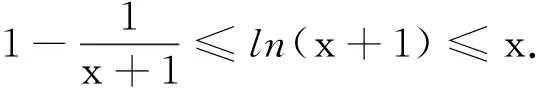
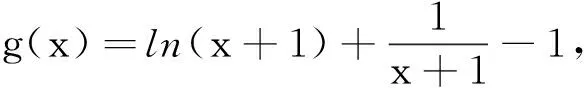
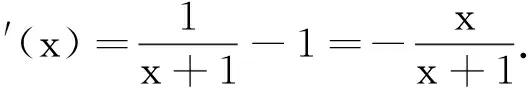
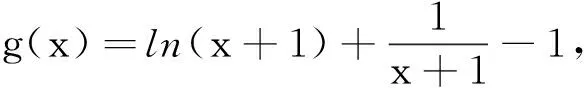
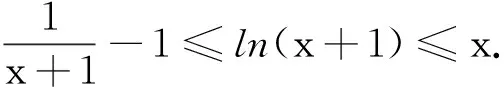
二、移

“移”指的是移项，即移动不等式中有关字母符号，调整其在不等式中的位置，将所证不等式的结构调整优化到合理的形式，将问题解决.

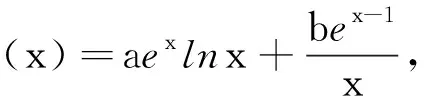
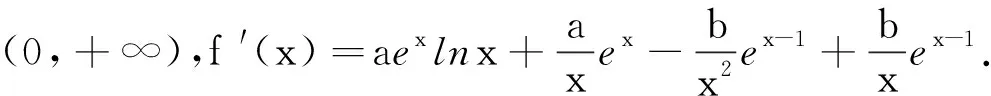
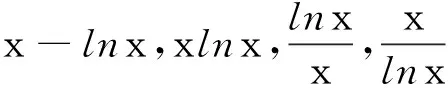
(2)注意：当x∈(a,b)时，f(x)min>g(x)max⟹f(x)>g(x)；

当x∈(a,b)时，f(x)>g(x)推不出f(x)min>g(x)max.

三、放

“放”指的是将不等式的一侧的值放大或者放小，将不等式的结构优化成合理结构，然后获得解决.放缩的依据是常用的几个不等式: ex≥x+1，lnx≤x-1，sinx≤x(x≥0)等.

例3 (2013全国数学课标卷Ⅱ理科) 已知函数f(x)=ex-ln(x+m)，

(1)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性；

(2)当m≤2时，证明f(x)>0.

解析(1)略.

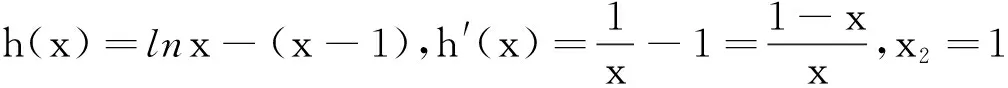
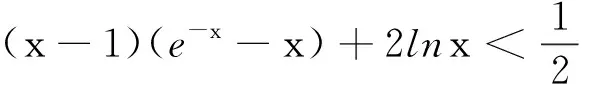
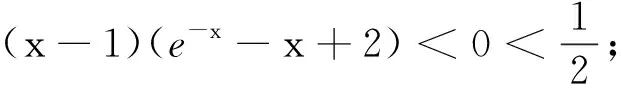
综上，命题得证.

点评本题从已知条件的重要不等式ln(x+1)≤x出发，直接进行证明，思路自然，过程流畅.在各类考试中，以ex≥x+1、ln(x+1)≤x为题根的试题屡见不鲜，应引起足够的重视，而且这些不等式源于课本上的习题.

四、分

“分”指的是分类讨论，当所证不等式情况复杂不能统一说明时，可根据题目的情况分情况讨论加以证明即可．

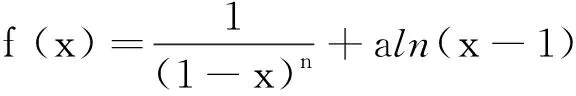
(1)当n=2时，求函数f(x)的极值；

(2)当a=1时，证明：对任意的正整数n，当x≥2时，f(x)≤x-1.

解析(1)略.

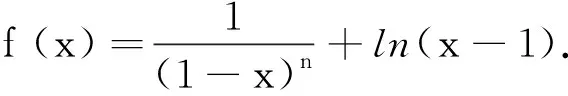
综上所述，结论成立．

说明本题根据n的奇偶性来分类讨论进行证明.

五、拆

“拆”指的是将所证不等式的一侧拆成两部分(或者多个部分)的和或者乘积的形式，然后分别研究每个函数的单调性、最值或者正负等情况，最后再综合起来考虑.

基本模式为：(1)要证f(x)>0(或者f(x)<0)先令f(x)=h(x)+m(x),将问题转化为证h(x)+m(x)>0(或者h(x)+m(x)<0)，具体操作上可以通过研究函数h(x)和m(x)的单调性、最值或者正负即可．(2)要证f(x)>0(或者f(x)<0)先令f(x)=h(x)m(x)将问题转化为证h(x)m(x)>0(或者h(x)m(x)<0)，具体操作上可以通过研究函数h(x)和m(x)的单调性、最值或者正负即可．

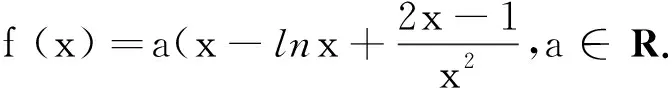
(1)讨论f(x)的单调性；

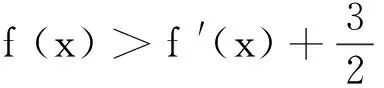
解析(1)略.

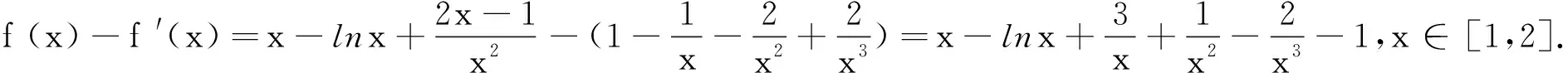
在利用这几种技巧来证明函数不等式时，我们的思路可以打开，具体操作上可根据题目合理选择方法.

从以上几例可以看出，要想利用导数证明函数不等式，掌握好相关的技巧是解决问题的关键，而“构、移、分、拆、放”这些技巧不是孤立的，应是相互交融，相互依赖的，真正期待“构、移、分、拆、放”五个绝招能帮助考生升入理想的高等学府.

参考文献：

[1]徐加华．利用搭桥法处理不等式中恒成立与能成立的“混搭”问题[J].数学通讯，2013(12)：26-28.