邹议高中物理常用的几种解题方法和技巧

王雨桐

(吉林省榆树市实验高级中学校 130400)

物理在高中课程中属于较难的一门学科，我们可以发现在学习到一定程度后考试成绩一直得不到提升，而且物理涉及的规律、法则等内容较多，即便掌握了教材当中的基础知识，在实际考试过程中遇到的很多问题依然没有思路和办法进行解决.其实物理和数学一样，大部分的知识都需要学生在理解的基础上，通过思维的分析过程再结合相应的思想方法进行处理，在答题方面主要表现为知识和题目信息的结合以及相关解题技巧的使用.然而，后者是需要学生在长期的训练中通过经验不断地进行总结，直到达到一定的熟练程度后便能够灵活地应用于答题.因此，在日常学习过程中，我们不但要总结和归类在练习中遇到的各类技巧和方法，而且要对它们进行专门地分析和研究，弄明白其主要的使用情景和方式，这样才能快速提升自身的物理解题实力.

一、整体思维法

“整体思维法”是在解决物理问题时经常用的一类思想方法，其主要是从全局的角度来看待静止的系统或者运动过程，从而省去中间部分繁琐的分析和推理环节，这样不但能够提高解题的效率，使得整个物理过程变得简单化、主观化，而且在节省时间的同时，可以提高我们答题的正确几率.

例1 如图1所示，车厢里悬挂着两个质量分别为m1、m2的小球(下面球的质量为m1)，当车厢向右做匀加速运动(空气阻力不计)，达到稳定状态时下列各图中正确的是( )

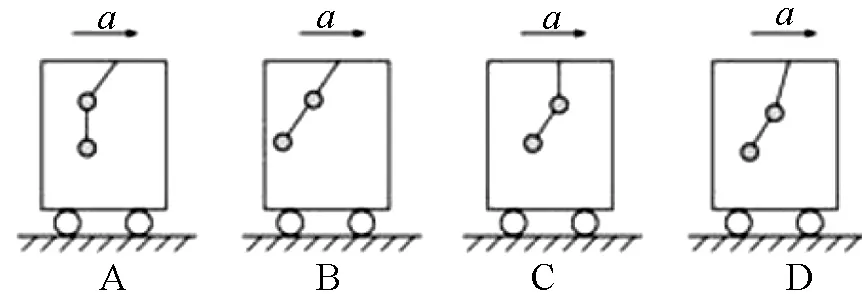
图1

在解答此题的过程中，很多学生会采用下述方式进行分析：对下面的小球m1受力分析，设细线与水平方向的夹角为θ，其主要受到了向下的重力和绳子的拉力，具体受力情况如图2甲所示，根据图中所示的内容可以我们可以知道tanθ=m1g/m1a=g/a；然后，对小球m2进行受力分析：重力和两根绳子分别在不同方向的拉力，假设上面的细绳与水平方向所成的角度为β，但是根据已知的信息并不能列出相关的方程.此时，就需要利用“整体思维法”将两球同时进行受力分析，假设拉上面小球的细线与水平方向的夹角为α，其具体受力情况如图2乙所示，由此便能够列出公式tanα=(m1+m2)g/(m1+m2)a=g/a，因而可知θ=α，故选项B正确.

图2

物理当中的很多过程分析都离不开“整体思维”，我们在实际解题活动中应该根据题目信息并结合“隔离”的思想充分考虑单个物体和整个系统之间的关系，争取用简单、有效的方式进行答题.

二、动态分析法

“动态分析法”主要用于分析一些平衡或者运动过程中的各个物理量的变化情况，需要我们学生具有牢固的知识基础和清晰思维，目前在考试当中经常会遇到针对此方法的相关题型，同时也是很多学生容易出现错误的地方.因此，我们更应该对此方法进行深入分析并掌握相关的技巧，从而提高答题的正确率.

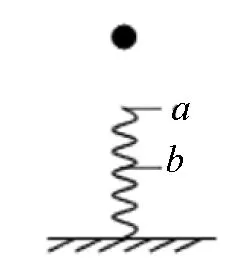
图3

例2 如图3所示，小球由高空自由落下，落在一竖直放置的轻弹簧上，球在a点与弹簧接触，在b点弹簧被压缩得最短，在球从a→b的过程中(不计空气阻力)，下列说法正确的是( )

A．小球的速度一直减少

B．小球的速度先增加后减小

C．小球的加速度先减后增

D．小球的加速度一直增加

分析在解答此题时，我们不能直接从选项入手，而是需要运用“动态分析法”弄明白小球在接触弹簧由a→b的整个过程中的受力变化情况，进而再对各个选项进行判断.具体分析过程如下：小球以一定的速度接触a之后，会直接向下压缩弹簧，其受到的弹力也在逐渐变大，重力不变，因而，合力不断减小且方向竖直向下；当重力和弹力大小相等时，速度达到最大；小球再向下移动时，合力开始变大且方向向上，到达b位置后速度的大小变为0.通过对小球具体运动情况的动态分析，便能够快速得出其速度和加速度的变化情况，正确选项为B、C.

此题在考试过程中有非常多的变型，如：判断重力势能、机械能等物理量的变化情况，因此，我们可以将动态分析的结果作为一种过程模型进行整理和总结，这样一来，在遇到相似问题后便能够直接从选项入手判断出正确的答案.

综上所述，物理学科当中的解题技巧和方法非常多，我们在实际学习过程中应该针对每一类题型进行深入分析，找出其中蕴含的思想或者方法，然后再将其迁移到同一类问题的解决中，这样我们不但能够提高答题的准确率，而且可以对物理产生更加深刻的认识.

参考文献：

[1]王维和.高中物理解题方法的选择与比较之我见[J].课程教育研究,2017(42):164-165.

[2]张澍洺.高中物理力学三大解题技巧探究[J].科技资讯,2016,14(24):85-86.

[3]刘波.论常用思维方法在高中物理解题中应用[J].数理化解题研究,2016(19):64.