图像、图形变化在数学解题中的应用

张震明

(山西省临汾第一中学校高三 041000)

一、方程中变量加(减)、乘(除)对曲线的几何意义

已知方程f(x,y)=0，则f(x+a,y)=0的曲线相当于原方程的曲线向左平移了a个单位.同理，f(x,y+a)=0的曲线相当于原方程的曲线向下方平移了a个单位.a为负数则视为反向平移.

已知方程f(x,y)=0，则f(ax,y)=0(a≠0)的曲线相当于原曲线所有点的x坐标变为原来的1/a倍.同理，f(x,ay)=0的曲线相当于原曲线所有点的y坐标变为原来的1/a倍.a为负数可视为“颠倒”.此变化我们可以称之为曲线的伸缩.

一般我们在高中阶段只学习了以上两种，由此我们可以得到方程f(ax+b)=0的曲线相当于原曲线先向左平移b个单位，再将所有点的x坐标变为原来1/a倍(y与x等价，此处及下面不再对y的加、乘进行讨论，同理即可).我们还可以进行一些简单的延伸：一般地，已知原方程f(x+b,y)=0(b∈R)，则f[a(x+b),y]=0(a≠0)的曲线相当于原方程曲线的所有的点到直线x+b=0的距离变为原来的1/a倍.

这些结论看起来比较复杂，但实际上理解起来非常简单：比如，若要使f(ax,y)等于零，即等于原来的f(x,y)，那么就要让a倍的“新x”等于“原来的x”，可以理解为对变化的“弥补”.

利用上述可以解释椭圆与圆的关系.

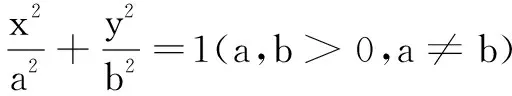
二、伸缩对图形面积的影响及其应用

对于任一平面封闭图形及任意一对相互垂直的两个方向，沿其中一个方向伸缩a倍，那么图形面积变为原来的|a|倍.a<0意味着图形会颠倒；a=0意味着图形缩成一条线段，面积为0.

由此我们可以立即得到椭圆的面积:假设圆的半径为a(a>0)，圆面积S=a2π，将该圆沿某一方向伸缩b/a(b≠a,b>0)倍，即得到椭圆(长、短轴为2b、2a或2a、2b)，椭圆面积S=a2π×(b/a)=abπ.

当我们遇到积分问题时，有的也可以用到以上思想.

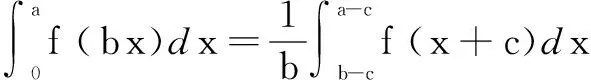
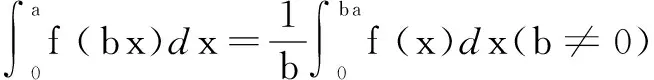
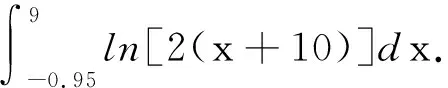
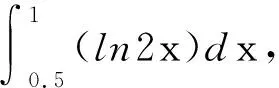
三、伸缩对直线斜率的影响及其应用

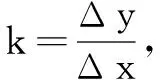
以此可以简单证明以下解析几何推论：

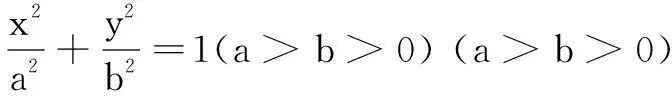
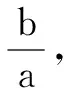
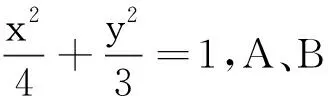
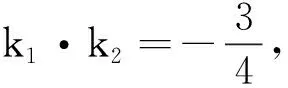
2.椭圆中心到椭圆上任意一点(非顶点)的直线的斜率与过该点的椭圆切线的斜率乘积为定值.

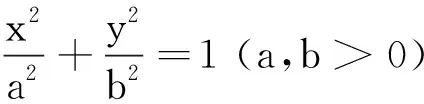
四、图形伸缩前后的不变关系及其应用

图形伸缩前后，以下关系不变：

1.面积比不变

若存在两个或多个封闭图形，均沿某个方向伸缩，其面积均成同样的比例扩大或缩小，面积比不变.

2.所在直线斜率相同的两条线段，长度比不变.

3.直线斜率比值不变，特别地，平行关系不变.

4.相切、相交、相离关系不变.

利用以上特点，可以解决一系列关于椭圆的题.

遇到求面积的最值问题、比值问题时，考虑利用面积比不变特点将椭圆伸缩成圆来研究，最后还原成椭圆得到答案.

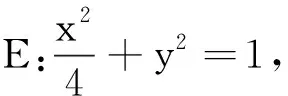
解析将椭圆的x坐标缩小一半，得到圆x2+y2=1.由面积比不变原理可知，圆中面积最大时，还原回椭圆中面积也最大；且满足S圆△OAB=0.5S椭圆△OAB①，直线斜率满足关系：k圆=2k椭圆②.

在圆中，S△OPQ=|OA|·|OB|·sin∠AOB=sin∠AOB.

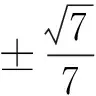
至此我们得到了圆中的最大面积和直线斜率，按照上面①②两个关系还原到椭圆即可.

五、对变量的加减在极坐标中的几何意义

即f(ρ,θ+φ)=0(ρ、θ为变量)的曲线可视为f(ρ,θ)=0的极坐标曲线以极点为中心按顺时针方向转了φ个单位，类似于直角坐标系的平移.

方便记忆，有：“顺加逆减”.

以上我们从曲线变化出发逐步讨论了方程与曲线之间的变化关系、变化的特点以及诸多应用，及其思想在其他坐标系的推广.利用曲线变化关系解决问题是一种较为创新又比较实用、便捷的思维方式.

参考文献：

[1]人民教育出版社，课程教材研究所，中学数学教材研究开发中心.普通高中课程标准实验教科书(选修)2-1(A版)[M].北京：人民教育出版社，2014.

[2]人民教育出版社，课程教材研究所，中学数学教材研究开发中心.普通高中课程标准实验教科书(选修)2-2(A版)[M].北京：人民教育出版社，2014.