基于随机过程与支持向量机构建期货配对交易策略

刘 辉，刘忠元，周伟杰

配对交易策略起源于美国的华尔街，是成熟资本市场的主流投资策略之一。该策略在美国股票市场一经推出，便获得了巨大成功。随着国内做空机制逐渐放松，基于统计套利的量化交易方式获得快速发展与应用。配对交易策略作为一种市场中性策略，其思想主要是指从市场上找出一对历史价格走势相近的标的进行配对，当配对标的之间的价差偏离历史均值时，做空价格较高的标的，做多价格较低的标的，当价格回复到均值附近时，结束头寸从而获得利润。

一、文献综述

关于配对交易，国外学者的研究已经形成了一套成熟的理论体系。代表性的理论方法包括Gatev等[1]提出的最小距离法、Vidyamurthy[2]提出的协整分析法以及Elliott等[3]提出的随机价差法。这些经典理论的提出为配对交易策略的实现提供了理论基础，其在金融市场上的实际应用证明了配对交易策略的商业价值。

配对交易策略的相关研究主要包括配对标的的选取和交易参数的设计两个方面。在配对标的选取方面，Gatev等[1]使用1962—2002年美国股票的日线收盘数据，通过最小距离法筛选出合适的配对股票组合。王春峰等[4]利用沪深300成分股2006—2009年的数据，对基于最小距离法的经典配对交易策略进行了实证测算。在交易参数设计方面，Huck[5]将神经网络方法和多属性决策理论相结合，使用神经网络技术对候选配对的价差进行预测，使用多属性决策技术对候选股票进行排序；唐国强等[6]利用切比雪夫不等式和夏普比率构建套利阈值统计量，研究了中国白糖期货合约数据的最优阈值以达到利润最大化。近年来，一些学者对配对交易方法进行评估比较。Bogomolov[7]将距离法、协整法和随机价差法应用于澳大利亚证券交易所，发现这三种方法每年都能得到5%～12%的收益。

但相关研究集中于证券市场，且选取的交易数据大多为日线数据。随着信息透明度和市场有效性的提高，传统配对交易策略在国内金融市场的收益变得越来越低。本文以国内商品期货市场为研究对象，通过O-U随机过程与支持向量机预测价差的变化趋势，构建了一种新型的配对交易策略。选取CZCE菜粕与DCE豆粕期货进行跨市套利，使用2015年9月8日至2017年9月8日的1分钟高频交易数据进行实证分析，研究表明，该新型配对交易策略在国内期货市场中具有可行性，其胜率和收益率明显优于传统配对交易策略。

二、模型与方法

(一)协整分析法

自Engle和Granger[8]提出了金融时间序列的协整理论和误差修正模型后，协整模型被广泛应用于时间序列建模。金融时间序列往往表现出非平稳性，而协整理论的贡献在于发现非平稳时间序列之间的线性关系，并进行线性组合为平稳序列。

本文采用EG两步法验证配对的两个金融时间序列之间是否存在协整关系。首先，单位根(ADF)检验。确定两个金融时间序列是否为同阶单整，如果是同阶单整，则进行最小二乘法(OLS)回归，计算出残差。然后，对残差进行ADF检验。如果残差平稳，则认为两个金融时间序列之间存在协整关系，否则认为两者不存在协整关系。

(二)O-U模型

(1)

(三)支持向量机模型

支持向量机是由Vapnik等人提出的一种分类算法，其基本模型是构建特征空间上的最大间隔线性分类器，通过寻求结构化风险最小来提高机器学习模型的泛化能力。线性分类器通过构建最优超平面将一组数据分为两类，这个线性超平面的一般形式f(x)=wTx+b，wT为权重，b为阈值。为使分类超平面的几何间隔达到最大值，可求解以下目标函数的最优化解。

(2)

通过拉格朗日对偶性转化和SMO算法可求最优解w*和b*。

(3)

(四)技术指标

现有研究只考虑了两种标的之间的价差(SPREAD)因素，忽略了交易过程的其他交易信息，而这些信息也为配对交易提供有价值的信息。因此，本文考虑了除价差外的其他多种技术指标差作为样本特征，选取了算数移动平均(SMA)、加权移动平均(WMA)、相对强弱(RSI)和资金流量指数(MFI)等4个技术指标。

在课堂上，教师可以利用虚拟现实技术设置包括导游讲解技巧和流程、处理突发事件、满足游客需求等任务的情景模拟，通过技能分解，帮助学生全方位感知自己的操作技能，提高课堂教学与实践实训的相似度，让学生在课堂上完成导游实战模拟，培养智慧型导游服务人才，大大缩减了学生就业后的适应时间，提高学生对于社会岗位的适应能力。

(4)

(5)

式中，WMAt为标的t时刻的WMA值，Wi为标的i时刻的权重。

(6)

式中，RSIt为标的t时刻的RSI值，RSt为标的t时刻前n个时刻内的涨跌幅均值比。

(7)

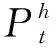
(五)构建样本特征和标签

首先，构建价差特征模型。

(8)

(9)

其次，样本过滤。通过比较前后价差的变化幅度，可判断每次交易是否获利，以达到划分标签的目的。为了排除前后价差变化幅度微小不足以获利的样本，根据以下算法对样本进行过滤。

(10)

(六)构建SVM预测模型

选用LIBSVM软件包训练数据，建立价差变化幅度预测模型。为了提高模型训练速度，避免原始数据中部分特征范围过大而另一部分特征范围过小，在建立训练模型之前需要对样本特征规范化至[0,1]之间。模型参数s设置为“C-SVC”，核函数类型设为线性核函数，然后使用训练好的SVM模型对测试集进行预测。

(七)构建交易信号

第一，开仓规则。选取1倍标准差作为开仓阈值，当价差标签为“+1”且价差偏离价差均值超过1倍标准差时，则执行开仓指令，即卖空相对被高估的标的，买入相对被低估的标的。

第二，平仓规则。开仓后当价差回复到均值附近时，则进行平仓操作。在本文中该平仓阈值选取0.2倍标准差。此外，由于本文选取的是1分钟期货的高频交易数据，不适合长期持有，因此设定当开仓后3个交易日内价差尚未到均值附近，则以第3个交易日的收盘价平仓头寸。

第三，止损规则。开仓后当价差继续偏离时，为了避免价差出现极端偏离而导致损失，需要设定止损线。本文设定止损线为2倍标准差，即当开仓后，价差继续偏离达到2倍标准差时，则执行平仓指令。

三、实证研究

(一)数据选取

菜粕的蛋白含量约36%，豆粕的蛋白含量约43%。这两种饲料具备可替代性。正常情况下，菜粕和豆粕具有较为稳定的价差，这使得CZCE菜粕与DCE豆粕的价格联系更加紧密，为菜粕豆粕的跨市套利提供了可行性[10]。本文选取CZCE菜粕与DCE豆粕期货1分钟高频交易数据进行实证研究，选取的时间区间为2015年9月8日至2017年9月8日，筛选出的样本点共计181 720个。

(二)数据检验

1.相关性分析

由图1可以直观地看出CZCE菜粕与DCE豆粕收盘价呈现趋同走势，两者的相关系数达到0.938 2，说明两者之间具有很高的线性相关关系。

CZCE菜粕与DCE豆粕收盘价的时间序列X，Y及其一阶差分序列的检验结果(见表1)表明，原始收盘价序列的单位根检验p值远大于0.000 1，接受原假设，即CZCE菜粕与DCE豆粕的时间序列为非平稳序列。一阶差分序列ADF检验结果表明，两者的p值远小于0.000 1，拒绝原假设，即一阶差分序列都为平稳序列。因此，CZCE菜粕与DCE豆粕1分钟收盘价时间序列同为一阶单整。

2.协整分析

根据CZCE菜粕与DCE豆粕1分钟收盘价建立协整回归方程，得到长期均衡关系X=0.881 3*

Y-189.642 8+resid(resid表示残差项)。R2=0.880 3，表明该协整回归模型与样本数据的拟合度较高。对resid进行ADF检验结果(见表2)表明，残差项不含有单位根，残差序列为平稳序列，该模型不存在伪回归现象。因此，CZCE菜粕与DCE豆粕1分钟收盘价之间存在协整关系。

(三)SVM预测结果分析

将CZCE菜粕与DCE豆粕181 720个样本数据进行标记筛选。标签“+1”与“-1”的样本数据基本均衡(见表3)。将数据集按80%—20%划分为训练集与测试集，其中训练集的时间跨度为2015年11月5日23时30分至2016年7月15日9时5分，测试集时间的跨度为2016年7月15日9时6分至2017年9月7日14时31分。

SVM模型预测结果如表4所示。TP/(TP+FP)表明该交易策略的胜率达到72.72%，TN/(TN+FP)表明该策略成功避免了95.60%的亏损交易。同时，预测亏损与预测盈利的个数分别为3 321与297，说明该模型为风险厌恶型。同时，该模型错过了1 463个交易获利机会，产生了81个交易亏损机会，说明此模型宁愿错过交易获利机会，也要避免潜在的亏损交易。结合配对交易策略的交易信号，测试集中3 518个样本点的套利时机如图2所示。

表1 单位根检验

注：原假设*为序列非平稳。

表2 残差单位根检验

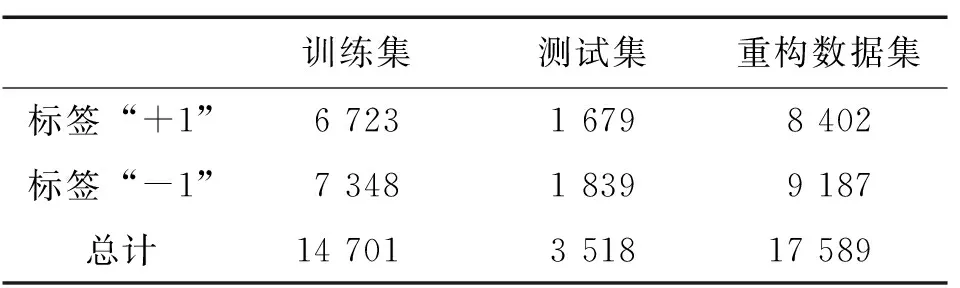
表3 样本标签结构

表4 SVM模型预测结果分析表

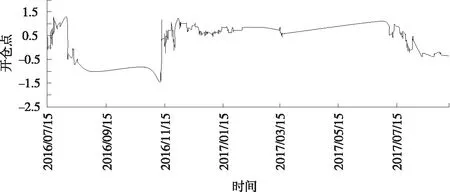
图2 新型配对交易开平仓示意图

(四)传统与新型配对交易策略比较

结合配对交易策略的套利规则，分别对传统与新型配对交易策略进行比较分析，模拟交易结果如表5所示。新型配对交易策略的胜率和收益率都大大优于传统配对交易策略，这说明本文描述的新型配对交易策略，提高了传统配对交易策略的胜率和收益率。

表5 传统与新型配对交易策略的对比表

四、结论

本文设计了一种基于O-U过程和SVM优化的配对交易策略。以2015年9月8日至2017年9月8日时间段内CZCE菜粕与DCE豆粕期货1分钟高频交易数据为研究对象，检验了该配对交易策略的可行性。结果表明，引入SVM模型对传统配对交易策略进行优化，能较好地预测出价差变化趋势，从而适度战胜市场；新型配对交易策略的胜率明显高于传统配对交易策略，降低了配对交易的亏损风险，使新型配对交易策略的获利能力大大提升。新的模型为配对交易策略提供了新的思路，有助于改善传统配对交易策略的收益现状，提升配对交易策略的获利能力。为获取更好的交易表现，新模型仍需进一步地改进，例如在样本特征方面可以引入更多优异的技术指标，或者对技术指标做PCA分析；此外，在标签划分标准方面采取的是单一标准，未来研究可以尝试多种划分标准。

参考文献：

[1]GATEV E，GOETZMANN W N，ROUWENHORST K G．Pairs trading：performance of a relative-value arbitrage rule[J]．Review of financial studies，2006，19(3)：797-827．

[2]VIDYAMURTHY G．Pairs trading：quantitative methods and analysis[M]．Hoboken：Wiley，2004：35-47．

[3]ELLIOTT R J，VANDER H J，MALCOLM W P．Pairs trading[J]．Quantitative finance，2005，5(3)：271-276．

[4]王春峰，林碧波，朱琳．基于股票价格差异的配对交易策略[J]．北京理工大学学报(社会科学版)，2013，15(1)：71-75．

[5]HUCK N．Pairs selection and outranking：an application to the S&P 100 index[J]．European journal of operational research，2009，196(2)：819-825．

[6]唐国强，高伟，覃良文，等．基于切比雪夫不等式的白糖高频数据统计套利[J]．统计与决策，2016，445(1)：87-90．

[7]BOGOMOLOV T．Pairs trading in the land down under[M]．Los Angeles：Social Science Electronic Publishing，2010：1-22．

[8]ENGLE R F，GRANGER C W J．Co-integration and error-correction：representation，estimation and testing[J]．Econometrica，1987，55(2)：251-276．

[9]黄晓薇，余湄，皮道羿．基于O-U过程的配对交易与市场效率研究[J]．管理评论，2015，27(1)：3-11．

[10]周伟杰，顾荣宝．股指期货和现货的线性、非线性Granger因果关系分析——基于1分钟高频数据的实证研究[J]．常州大学学报(社会科学版)，2015，16(4)：45-51．