基于改进快速扩展随机树算法的双机械臂协同避障规划方法

陈波芝 陆 亮 雷新宇 赵 萍

合肥工业大学机械工程学院，合肥，230009

0 引言

随着科学技术的进步和现代工业的发展，各种类型的机械臂在各个行业得到了越来越多的应用［1-3］。对于很多实际生产需求而言，仅由一般的单机械臂来进行操作不足以完成相对复杂的任务。两个机械臂相互协调、配合地完成作业的形式能够适应工作任务中不断提高的复杂性、智能性以及系统柔顺性的要求，因此双臂机器人成为研究和应用热点［4］。双臂机器人不同于两个单臂机器人的简单组合，它们在共同的工作空间内运动时，机械臂与空间障碍物以及双臂彼此之间可能发生干涉碰撞，导致故障，故需要对机械臂与环境之间的碰撞以及两臂之间的碰撞进行一定程度上的配合协调处理。在双臂机器人运动规划的研究中，如何避免这两类碰撞是关键问题之一［4-6］。

在机器人运动规划领域中，KIM等［7］提出一种适用于装配任务系统的改进快速扩展随机树（rapidly-exploring random tree，RRT）算法。该系统主要用于较困难的装配，如非线性配合工件的装配，既有两个机械臂首次的抓取组装策略，又有一个机械臂握持工件，另一个机械臂改变位置再抓取的组装策略，采用该算法生成装配路径、相关路径和再抓取路径，可以满足对复杂装配的要求，但在求解相关路径时，使用参数较多，计算十分复杂，较难应用于实际。LI等［8］提出一种将高斯分布用于RRT算法的方法，该方法将传统RRT算法中的随机采样用高斯分布采样代替，将目标位置设为期望值，将算法步长设为标准差，通过调整标准差的大小来调节算法的步长，进而调节算法向目标位置收敛的速度，但标准差设置不合适时，该算法会出现无解的情况。谢碧云等［9］提出基于双向RRT算法的运动规划技术，该技术主要用于7R机械臂的避障达点运动中，在双向RRT算法给出目标位形树时，结合末端姿态调整与7R机械臂的解析逆解来生成目标位形，但算法需要以目标位置为输入，并且需要通过机械臂的逆运动学获得多组目标的关节姿态，再建立双向随机扩展树，计算量较大，而且不能适应于动态环境。王道威等［10］在对RRT算法进行改进的基础上，提出了一种动态步长的RRT路径规划算法，该方法可以有效地降低算法的时间复杂度，但是该论文未给出动态步长的数学计算公式，其数值变化的确定主要靠经验。杜明博等［11］提出一种基于连续曲率RRT算法的智能车辆运动规划算法，引入目标偏向采样策略以及合理的度量函数以提高规划速度，采用一种基于最大曲率约束的后处理方法来生成平滑且曲率连续的可执行轨迹，但该方法在目标采样策略中的阈值选择较为繁琐且仅限于对车辆进行运动规划。刘成菊等［12］提出基于改进RRT算法的RoboCup机器人动态路径规划方法，该算法的主要特点是以一定概率选择目标点，增加引力分量，对路径进行平滑处理，并引入路径缓存区生成动态扩展随机树，可以缩短路径约20%的长度，但当动态障碍物距离规划路径的起始点和目标点较近时，算法很容易发生振荡，导致机器人原地打转。关英姿等［13］提出空间自由漂浮机器人抓捕运动目标的路径规划方法，对于视线遮挡约束问题，采用扩展卡尔曼滤波器来建立目标运动状态估计器，在遮挡区域采用滚动RRT方法，在未遮挡区域采用比例导引算法使机械臂向目标位置不断接近。该方法可以进行有效的运动状态估计并快速可靠地实施抓捕，但在两个算法切换时，容易因为目标估计的延迟而产生振动，导致算法失效。

本文以双臂机器人为研究对象，在传统RRT算法的基础上，引入罚函数和碰撞检测，通过将主机械臂的运动和位置转化为从机械臂的动态障碍物的方法，进行双臂机器人的协同避障运动规划的研究，给定双臂机器人的尺寸参数以及工作环境中的障碍信息，最终可规划一条使得各关节角平稳转动的双臂整体协同避障运动轨迹，且算法具有较快的收敛速度和较好的精度。

1 机械臂双臂运动学建模

本文以一种六自由度双臂机器人为例，根据D-H建模方法得到主从机械臂的关节示意图（图1）及其D-H参数（表1）。其中，从机械臂的关节示意图与主机械臂的关节示意图以机器人本体为镜像对称。主机械臂的D-H参数α、θ与从机械臂D-H参数互为相反数。

图1 主机械臂关节示意图Fig.1 Joint diagram of main robot arm

表1 主机械臂的D-H参数Tab.1 D-H parameter of main robot arm

由D-H法，我们已获得2个机械臂的构型参数，接下来需要在算法中建立主从机械臂运动的对象。首先利用Robotics Toolbox中的函数link和robot建立双臂的运动对象，然后建立六自由度机械臂的正运动学方程，得到机械臂6个关节的位置。

逆运动学求解主要有三个方面的问题：①逆解的存在性问题。在机械臂的工作空间内必须存在期望位姿。②逆解的多解性问题。逆解的数目主要取决于机械臂的结构连杆参数中的连杆长度和偏距中非零项的个数。一般说来，六自由度双臂机械人最多存在16组运动学逆解。③逆解的求解方法，包括数值解法和解析解法两种。

对于双机械臂机器人运动路径规划问题，一般都是根据其期望末端位姿进行逆解的。对多自由度双机械臂进行逆解时，有两个主要问题需要解决：①由于奇点位置的存在，有些位置无法进行逆解。②由于逆解的多解性，逆解不唯一的情况可能会导致机械臂有多个可行的解，而多个可行解会导致机械臂从上一个状态到下一个状态时，各关节角变化相差较大，使机械臂运动不稳定。

考虑到以上逆解求解存在的问题，本文提出了一种基于改进RRT算法的双臂机器人的运动规划方法：将改进的RRT算法与机器人正运动学相结合来避免对逆运动学进行求解，在通过运动规划算法求得符合目标位置精度的可行路径之后，经过一次末端位姿微调来消除目标误差，使最终得到的运动路径可以精确到达目标位置。

2 改进RRT算法的描述

2.1 RRT算法的基本原理

RRT算法［14］是一种基于随机采样的路径规划算法，在处理非完整约束的路径规划问题时具有相当大的优势。它可以将各种约束集成到算法之中，对环境要求较低，而且该算法在概率上具有完备性，理论上肯定能找到可行路径，但其缺点是搜索过于平均，算法效率较低，且规划出的路径往往偏离最短路径。针对RRT算法的缺点，本文提出了基于RRT的改进算法，用于双臂机器人的无碰路径规划。

2.2 基于改进RRT算法的双机械臂避障路径规划

首先，将两条机械臂中的一条作为主臂，一条作为从臂，建立障碍环境，同时，将机器人本体也作为障碍；其次，利用路径规划算法，在障碍环境中规划出主臂的一条可行路径；再次，将主臂作为动态障碍，对从臂规划出一条可行路径。算法总体流程见图2，其中，障碍物环境的建立、extendTreeRobot函数以及碰撞检测是本算法的关键改进。

图2 算法总体流程图Fig.2 Algorithm overview flow chart

2.2.1 利用障碍物函数建立避障环境

球型障碍物的参数少（仅有球心坐标和半径），可以降低算法的复杂度以提升其搜索效率，所以本算法采用球型包络不规则障碍物。

主臂进行路径规划时，只需考虑静态障碍物。从臂进行路径规划时，除了静态障碍物，还需要将主臂考虑为动态障碍物，将主臂的各个杆件的首末端和中点作为球心，根据机械臂尺寸大小可得障碍物的半径，建立动态障碍物。

2.2.2 extendTreeRobot函数

路径规划时，以障碍物空间中的机械臂的起始位姿节点为根位姿节点，通过罚函数采样逐渐增加叶位姿节点的方式，生成一个随机扩展树。当随机树中的叶位姿节点包含机械臂目标位姿区域时，便可在随机树中找到一条从起始位姿到目标位姿的路径。

本文对RRT算法的节点扩展进行了改进，主要通过对extendTreeRobot函数增加代价函数和快速收敛策略来实现。

本文建立的罚函数如下：

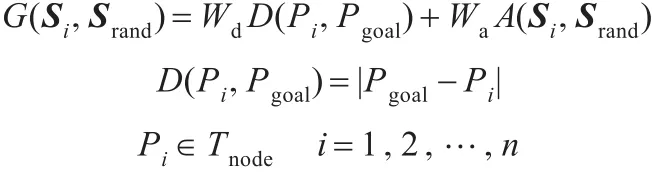
其中，G(Si,Srand)为算法已规划的位姿Si到当前的随机位姿Srand的路径代价；D(Pi,Pgoal)为Si状态下的机械臂末端的位置Pi到目标位置Pgoal的距离代价；Tnode为算法所生成的随机树，距离代价越小表示末端位置越优；A(Si,Srand)为机械臂位姿Si到随机位姿Srand的各个关节角的角度变化程度，越小表示机械臂运动越平稳；Wd、Wa分别为末端位置的最优性和机械臂运动的平稳性的权重。

用相邻两个位姿各个关节角的变化程度表示机械臂运动平稳性的优劣，定义相邻两个位姿的关节角变化程度：

其中，机械臂位姿Si表示算法已经规划的位姿中的第i个位姿下，机械臂各个关节的一组关节角；随机位姿Srand表示在随机位姿下，机械臂各个关节的一组关节角。

由于双臂机器人的尺寸和工作空间都较大，所以快速扩展随机树函数的搜索空间也很大，导致搜索效率下降。为提高算法的搜索效率，对所遍历过的机械臂的位姿节点进行择优筛选。代价函数的存在使得机械臂从起始位姿到目标位姿的搜索过程可以看作是一个逐渐寻优的过程，因而可以进行剪枝，剔除一些次优解以便减小算法的遍历空间，从而提高搜索效率。当机械臂使用本文算法搜索目标位姿时，先设定一个误差范围。当前位姿节点处机械臂的末端位置与随机位姿节点处机械臂末端位置间的距离小于设定误差时，就将该位姿节点加入算法的遍历空间，反之就将其剔除。在通过运动规划算法求得符合目标位置精度的可行路径之后，利用一种避免碰撞的位姿调整策略［15］，对机械臂的目标末端位姿进行一次微调，消除对目标位置产生的误差，使最终得到的机械臂运动路径是可以精确到达目标位置的运动路径。

该子函数流程如下：

（1）从机械臂6个关节中随机选取一个关节，例如关节2，确定算法步长为5°。

（2）在-90°～90°的闭区间内，每隔5°随机选取一个角度，如果角度为正，就顺时针转5°，如果角度为负，就逆时针转5°。假设随机选取到的角度为正。

（3）让关节2在初始角度1的基础上顺时针转5°，把当前位置记为随机树子节点角度2，把初始角度1记为子节点的父节点。

（4）从6个关节中随机选取一个关节，例如关节3。

（5）从-90°～90°的闭区间内，每隔5°随机选取一个角度，例如，随机选取到30°。

（6）让关节3在随机树子节点角度2的基础上顺时针转5°，记为随机角度1。

（7）建立代价函数。

（8）如果随机树子节点角度2的代价函数值最小，那么，就让关节3在随机树子节点角度2的基础上顺时针转5°，记为随机树子节点角度3。

（9）进行快速收敛。

（10）调用Robotics Toolbox中的函数使得角度一一对应6个关节的位置。

（11）调用collisionrobot避障函数避免主臂与障碍物发生碰撞。

（12）以此类推，直至找到的新节点与目标节点之间的距离小于给定误差范围时，函数结束循环。

（13）对最后一步末端位姿进行微调，到达精确目标位置。

该子函数表示如下：

Function1：extendTreeRobot Input：Sstart，Pstart，Pgoal，L，Ssatrt∈Sfree，Tnode，T Output：Spath，T

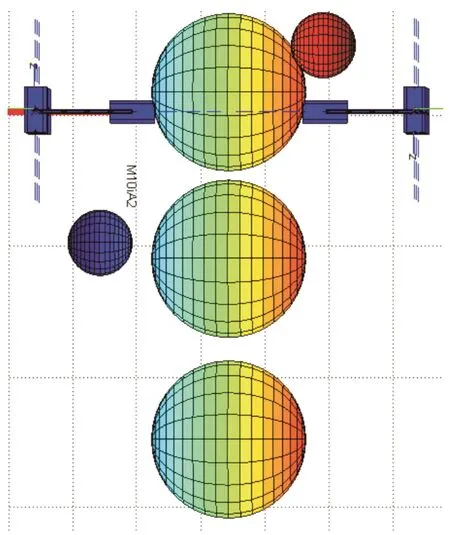
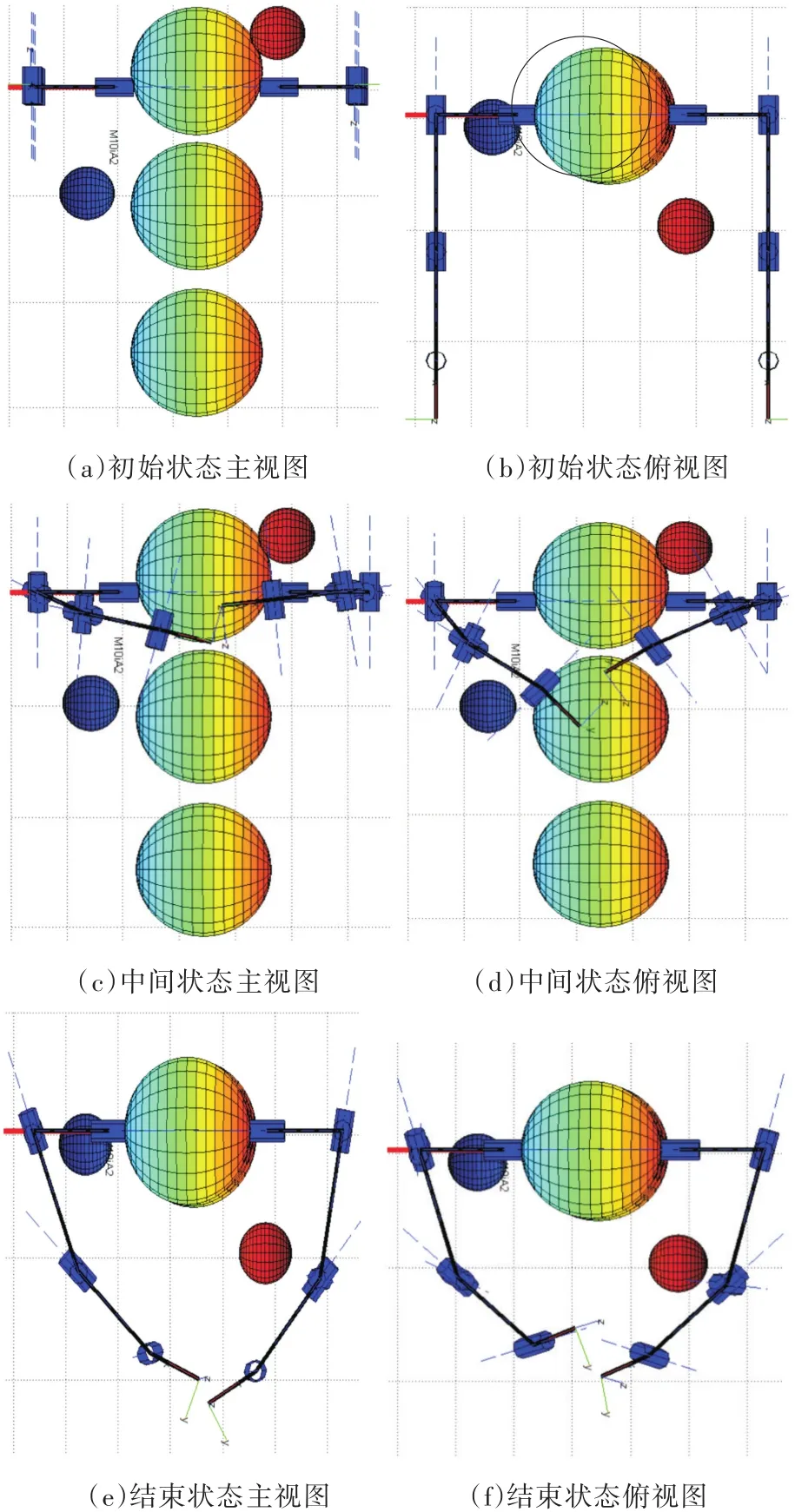
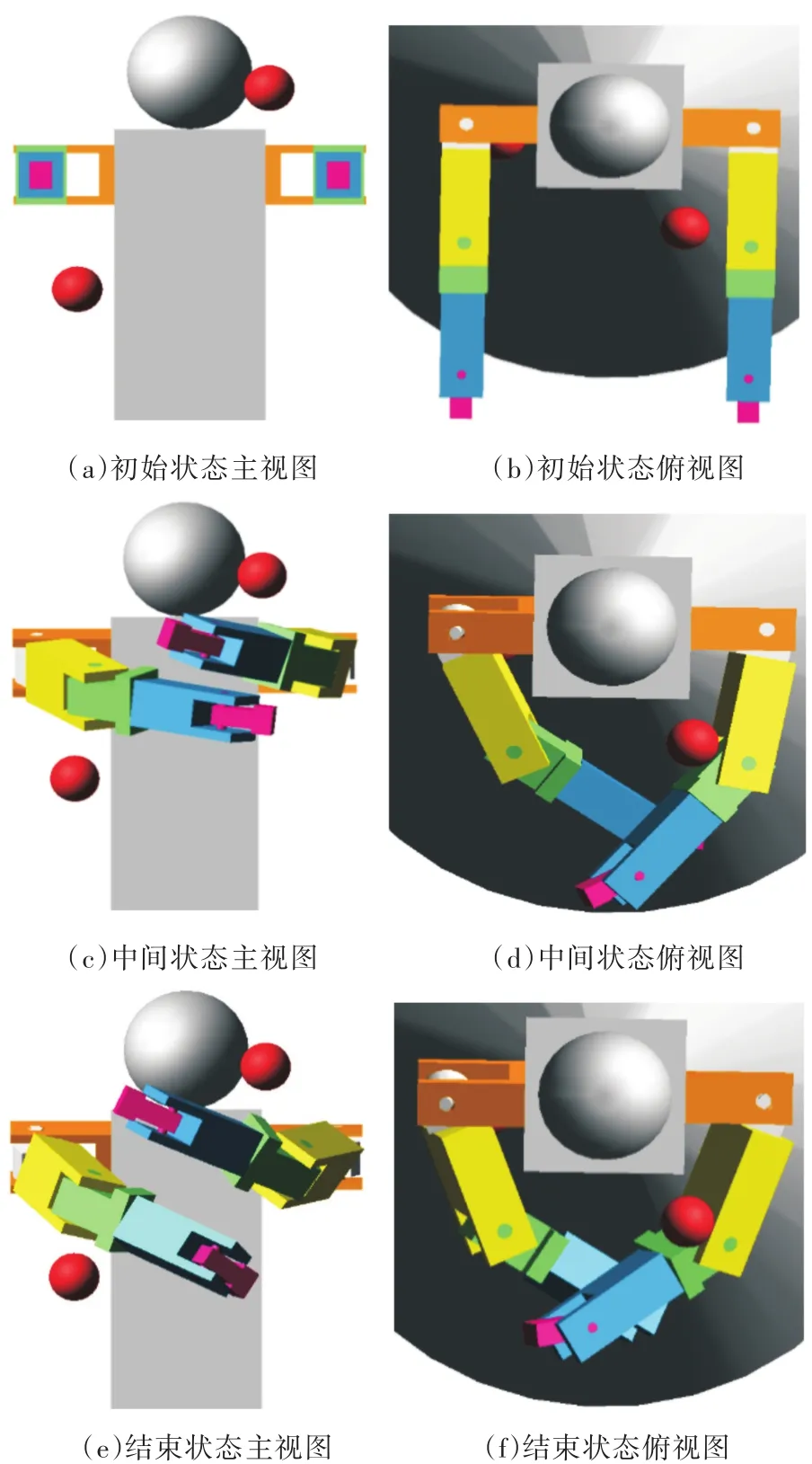
1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.初始化一个空位姿S和一个空节点P while|Pstart-Pgoal|＞L do Srand=随机节点（Sfree）Prand=ForwardKinematics（Srand）；end if optimal

2.2.3 碰撞检测

考虑机械臂与障碍物、机械臂与机械臂是否发生碰撞时，只需考虑机械臂与包络障碍物的球体的球心位置即可。考虑本文的机械臂与障碍物的实际大小、机械臂本体的大小，将障碍物进行膨胀，使障碍物的半径变为1.5倍障碍物的半径，以确保不会发生碰撞。

主臂进行碰撞检测时，需保证主臂的各个关节以及杆件中点与静态障碍物球心的距离大于1.5倍静态障碍物的半径。

从臂进行碰撞检测时，除了保证与静态障碍物不发生碰撞，还需保证与动态障碍物不发生碰撞。所以从臂的各个关节以及杆件中点与静态障碍物、动态障碍物球心的距离大于1.5倍障碍物的半径。

该子函数表示如下：

（x1，x2，x3，…，xn）表示n个关节的位置R表示障碍物的半径，C表示障碍物的球心O1=x1，O2=（x1+x2）/2，O3=x2 if‖O1-C‖<1.5…R and‖O2-C‖<1.5…R and‖O3-C‖<1.5…R then CollisionCheck（S）=1 end Function2：collision Input：（x1，x2，x3，…，xn），obstacle Output：CollisionCheck（S）1.2.3.4.5.6.7.

3 仿真实验验证及结果分析

3.1 MATLAB双臂机器人环境模型

如图3所示，代表机器人本体的球体障碍物是竖直排列以坐标（0，30 mm，150 mm）、（0，-224.2 mm，150 mm）、（0，-500 mm，150 mm）为球心、半径为140 mm的球体，其余的2个障碍物是球心坐标（-200 mm，100 mm，300 mm）、半径50 mm的球体，和球心坐标（-20 mm，100 mm，-300 mm）、半径50 mm的球体。主臂（左臂）初始状态时，关节1～6的6个关节角均为0°，主臂的末端位置坐标为（-545 mm，0，-145 mm）。从臂（右臂）初始状态时，关节1～6的6个关节角均为0°，从臂的末端位置坐标为（-545 mm，0，445 mm）。

图3 双臂机器人模型Fig.3 Dual-arm robot model

3.2 MATLAB数值仿真

利用MATLAB和Robotic Toolbox模型对所提出的算法进行仿真实验验证。设置主臂目标点的位置坐标为（-300 mm，-250 mm，100 mm）。从臂目标点的位置为（-410 mm，-150 mm，150 mm），目标位置精度为25 mm，即当机械臂的末端位置到达离目标点的距离小于25 mm时，算法即判定机械臂已到达目标位置。

MATLAB仿真结果如图4a、图4c、图4e所示，图4b、图4d、图4f为对应的俯视图。可以看出，双臂机器人的两个机械臂从指定的初始位姿协调无碰的运动到达指定的目标位姿，从而验证了算法具有有效性以及可行性。

图4MATLAB仿真结果Fig.4 Simulation results of MATLAB

图5 a所示为MTLAB仿真实验中主臂6个关节角完成一组运动转过的角度，图5b所示为从臂6个关节角完成一组运动转过的角度。

3.3 ADAMS样机验证

为了进一步验证上述数值仿真的结果，在ADAMS仿真分析软件上进行验证。图6a、图6c、图6e所示为在虚拟样机下的一组实验结果，图6b、图6d、图6f为对应的俯视图，确认其与障碍物不发生碰撞。

图5 主从臂关节角变化Fig.5 Main and second arm joint angle changes

图6 虚拟样机仿真实验结果Fig.6 Experimental results of virtual prototypes

4 结论

利用提出的改进RRT算法可以实现双臂机器人动态协同避障的运动规划，该算法在运动规划过程中利用机器人正运动学求解机械臂的位置，避免了对逆运动学进行求解，并且在经典RRT算法的基础上加入代价函数，从而可以搜索出较优的避障路径。主从机械臂前后两组动作有且仅有一组关节角发生变化（变化的值由算法的步长决定），相较于6个关节同时动作，该算法所得的运动轨迹较为平稳。利用节点剪枝择优和设立目标区域的方式达到快速收敛，提高了算法的搜索效率。通过运动规划算法求得的可行路径符合目标位置精度后，经过一次末端位姿微调消除目标误差，使最终得到的机械臂运动路径精确到达目标位置。将Solidworks中建好的双臂机器人的模型导入ADAMS生成虚拟样机进行仿真实验，验证了算法的有效性和可行性。

［1］ 刘宏，蒋再男，刘业超.空间机械臂技术发展综述［J］.载人航天，2015，21（5）：435-443.LIU Hong，JIANG Zainan，LIU Yechao.Review of Space Manipulator Technology［J］.Manned Space Flight，2015，21（5）：435-443.

［2］ 王恒升，陈伟锋，王思远.基于末端杆件螺旋运动的凿岩机械臂孔序规划［J］.中国机械工程，2016，27（13）：1748-1754.WANG Hengsheng，CHEN Weifeng，WANG Siyuan.Drilling Sequence Planning Based on Screw Motion of End Lever of a Tunneling Rig Manipulator［J］.China Mechanical Engineering，2016，27（13）：1748-1754.

［3］ 计时鸣，黄希欢.工业机器人技术的发展与应用综述［J］.机电工程，2015，32（1）：1-13.JI Shiming，HUANG Xihuan.Review of Development and Application of Industrial Robot Technology［J］.Journal of Mechanical ＆ Electrical Engineering，2015，32（1）：1-13.

［4］ 王美玲.面向救援任务的双臂机器人协作运动规划与控制方法研究［D］.合肥：中国科学技术大学，2015.WANG Meiling.Research on Cooperative Motion Plan⁃ning and Control of a Redundant Dual-arm Robot for Rescuing Tasks［D］.Heifei：University of Science and Technology of China，2015.

［5］ 胡雨滨.移动机器人双六自由度机械臂运动规划［D］.哈尔滨：哈尔滨工业的大学，2009.HU Yubin.The Motion Planning of Dual 6-DOF Arms of a Mobile Robot［D］.Harbin：Harbin Institute of Technology，2009.

［6］ 康浩博.基于改进蚁群算法的机器人双臂无碰撞路径规划［D］.沈阳：东北大学，2010.KANG Haobo.Mechanical Dual-arms'Collision-free Path Planning of Robot Based on Improved Ant Colony Algorithms［D］.Shenyang：Northeastern University，2010.

［7］ KIM D H，LIM S J，LEE D H，et al.A RRT-based Mo⁃tion Planning of Dual-arm Robot for（Dis）assembly Tasks［C］//International Symposium on Robotics.Seoul，2014：1-6.

［8］ LI Y，SHAO J.A Revised Gaussian Distribution Sam⁃pling Scheme Based on RRT*Algorithms in Robot Mo⁃tion Planning［C］//International Conference on Con⁃trol，Automation and Robotics.Nagoya，2017：22-26.

［9］ 谢碧云，赵京，刘宇.基于快速扩展随机树的7R机械臂避障达点运动规划［J］.机械工程学报，2012，48（3）：64-69.XIE Biyun，ZHAO Jing，LIU Yu.Motion Planning of Reaching Point Movements for 7R Robotic Manipula⁃tors in Obstacle Environment Based on Rapidly-explor⁃ing Random Tree Algorithm［J］.Journal of Mechanical Engineering，2012，48（3）：64-69.

［10］ 王道威，朱明富，刘慧.动态步长的RRT路径规划算 法［J］.计 算 机 技 术 与 发 展 ，2016，26（3）：105-107.WANG Daowei，ZHU Mingfu，LIU Hui.Rapidly-ex⁃ploring Random Tree Algorithm Based on Dynamic Step［J］.Computer Technology and Development，2016，26（3）：105-107.

［11］ 杜明博，梅涛，陈佳佳，等.复杂环境下基于RRT的智能车辆运动规划算法［J］.机器人，2015，37（4）：443-450.DU Mingbo，MEI Tao，CHEN Jiajia，et al.RRT-based Motion Planning Algorithm for Intelligent Vehicle in Complex Environments［J］.Robot，2015，37（4）：443-450.

［12］ 刘成菊，韩俊强，安康.基于改进RRT算法的Robo⁃Cup机器人动态路径规划［J］.机器人，2017，39（1）：8-15.LIU Chengju，HAN Junqiang，AN Kang.Dynamic Path Planning Based on an Improved RRT Algorithm for RoboCup Robot［J］.Robot，2017，39（1）：8-15.

［13］ 关英姿，宋春林，董惠娟.空间自由漂浮机器人对运动目标抓捕的路径规划［J］.机器人，2017，39（6）：803-811.GUAN Yingzi，SONG Chunlin，DONG Huijuan.Path Planning of the Free-floating Manipulator for Captur⁃ing a Moving Target［J］.Robot，2017，39（6）：803-811.

［14］ LAVALLE S M，KUFFNER J J.Randomized Kinody⁃namic Motion Planning［J］.International Journal of Robotics Research，1999，20（5）：378-400.

［15］ 宗成星，陆亮，雷新宇，等.一种基于A*算法的空间多自由度机械臂路径规划方法［J］.合肥工业大学学报（自然科学版），2017，40（2）：164-168.ZONG Chengxing，LU liang，LEI Xinyu，et al.A Path Planning Approach for Multi-DOF Spatial Manipula⁃tor via A*Algorithm［J］.Journal of Hefei University of Technology（Natural Science Edition），2017，40（2）：164-168.