改进熵权逼近理想解排序法的航空发动机限寿件模糊风险评估

李元斌 孙有朝 李龙彪

1.南京航空航天大学民航学院，南京，211106 2.武警士官学校机械系，杭州，310023

0 引言

国产大型客机发动机验证机CJ-1000AX完成首台整机装配，为后续开展试验验证与风险评估等工作提供了有力支撑，而对寿命限制件（简称限寿件）进行安全风险评估是其中一项重要内容。航空发动机适航规章对发动机限寿件进行了定义，失效会造成发动机灾难性后果的转子和静子结构件即发动机限寿件［1-5］，其性能对航空发动机适航性、安全性、可靠性和维修性产生关键影响。危害性矩阵分析法是航空航天领域判定故障模式危害度的常用方法之一，能够指明风险优先顺序，但在分析中只能手工绘制矩阵图，因绘图速度缓慢导致危害性矩阵分析法效率较低。故障模式点的纵坐标、横坐标（即危害度和严重度）以及故障模式点向对角线作垂线所得的垂点，在手工绘制时很难精确标出，造成故障模式危害性排序出现人为误差［6-8］。陈政平等［9］分析了传统风险优先数（risk priority number，RPN）法存在的 RPN值重复和灵敏度低等弊端，提出了一种基于费用损失和工艺故障模式发生概率的定性和定量相结合的RPN分析方法。针对危害性矩阵分析法和传统RPN法的不足，有学者使用熵权逼近理想解排序（TOPSIS）法对限寿件故障风险进行排序与评估。纪江明［10］使用熵权TOPSIS法对中国城市公共服务满意度进行了研究。本文针对限寿件故障数据较少且为小子样的情况，运用熵权法确定风险指标的信息熵权，并作为加权向量对规范决策矩阵进行修正，利用改进的熵权TOPSIS法更准确快速地评估限寿件故障模式的危害程度。

1 限寿件风险指标评估准则及其三角模糊数描述

故障模式影响分析（failure mode and effect analysis，FMEA）方法是风险评估的常用方法之一［11-16］，它通过计算风险优先数对评估对象的安全风险进行定量评估。风险优先数R是事件发生的严重度S、发生频度O和被检测难易度D三者的乘积，即R=SOD。R值可在1～384之间变化，其数值愈大，潜在安全风险愈高，可以使用RPN阈值来决定是否需要采取纠正措施，而优先措施的选取应当建立在严重度、发生频度和被检测难易度分析上。为了便于和传统RPN法进行比较，同时避免此算法的弊端，本文将严重度、发生频度和被检测难易度作为限寿件风险指标，确定其风险等级评估准则，并将3个风险指标模糊化，结合改进熵权TOPSIS法开展限寿件风险评估研究。

严重度指潜在故障模式造成最严重后果的等级，从无后果到无警告的严重危害后果，见表1。凡是严重度等级达到7或8的故障模式必须采取控制手段，以降低其严重度数值，有时甚至要求对该产品进行重新设计等。严重度等级小于或等于6时，应优先考虑发生频度高、被检测难易度高的故障模式。

发生频度指特定的失效起因或机理发生的频率，从极少发生到经常发生，见表2。

表1 严重度评估准则及其三角模糊数描述Tab.1 Evaluation criteria and triangular fuzzy number of severity

表2 发生频度评估准则及其三角模糊数描述Tab.2 Evaluation criteria and triangular fuzzy number of occurrence

被检测难易度指失效起因或机理的不可检测程度，从可直接检测出到完全无法探测，见表3。

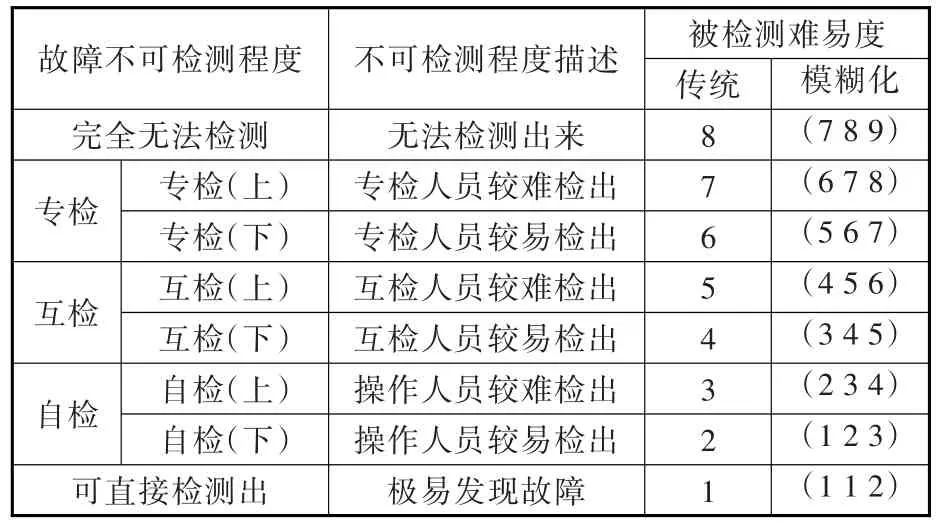
表3 被检测难易度评估准则及其三角模糊数描述Tab.3 Evaluation criteria and triangular fuzzy number of detection

建立风险指标评估准则后，可对3个风险指标进行等级评估。专家很难评估出3个风险指标的原始值，却容易用语言做出模糊评述。可以使用三角模糊数将定性语言评述转变为定量数据分析，进行定量计算。三角模糊数运用到限寿件风险评估中，很好地解决了定量评估需要与只能用定性语言评述之间的矛盾。

如果 a=[awavau]，其中，0＜aw≤av≤au，且aw为a的下边界，au为a的上边界，av为a的中值，则称a为一个三角模糊数。根据三角模糊数的定义和运算性质［17］，严重度、发生频度和被检测难易度的三角模糊数描述分别见表1～表3。

2 改进熵权TOPSIS的限寿件风险评估方法

熵权TOPSIS法是熵值赋权法和TOPSIS法的组合。熵（entropy）源于热力学，后来由Shannon引入信息论，可以计算信息熵的属性权重。TOP⁃SIS全称为逼近理想解排序（technique for order preference by similarity to ideal solution），是Hwang、Yoon提出的按相对接近度进行排序的多因素综合评估方法［18-20］。

2.1 改进熵权TOPSIS法分析步骤

改进熵权TOPSIS法分析步骤如下：建立原始决策矩阵，并进行量纲一化和归一化等规范化处理，得到规范决策矩阵，用熵权法确定属性权重作为加权向量，对规范决策矩阵进行修正。找出多个目标中的最优解和最劣解（分别用正负理想解表示），然后计算各评估对象与正负理想解的距离，得到其与理想解的相对接近度，由相对接近度大小排序进行评估决策。具体计算步骤如下：

（1）建立原始决策矩阵。设由n个属性构成一个指标体系来评估m个方案的优劣，第i个评估对象的第 j个指标的值为 yij(i=1,2,…,m;j=1,2,…,n)，得到各个方案的特征值模糊矩阵Y=(yij)m×n。

（2）求解规范决策矩阵。考虑到是对FMEA方法中的故障模式进行分析评估，釆用基于成本型的模糊决策矩阵规范方法［21］，把决策矩阵Y={y}转化为规范决策矩阵 Z={z}={()}，即

式中，为评估值的下边界；为评估值的上边界；为评估值的中值。

（3）用熵权法确定属性权重。按照信息熵算法，在决策中获得信息的多少和质量是决策精度和可靠性水平的决定因素之一。利用此算法得出的熵权作为属性权重，熵权越大，权重越大，对应指标属性就越重要。考虑到目前限寿件故障数据较少，为小子样数据，使用相关专家和工程人员的决策信息来计算风险指标的熵权。

l位专家和工程人员提供了限寿件风险指标S、O、D的决策信息，可得到原始数据矩阵E=(eij)l×3。利用极值法对矩阵E进行标准化处理，得到矩阵 F=(fij)l×3，有

第 j项指标下第i位专家和工程人员决策值的比重

第 j项指标的信息熵

指标差异度

（4）求解加权规范决策矩阵。将熵权法确定的属性权重作为加权向量，对规范决策矩阵进行修正。每一属性权重与其对应的矩阵元素相乘，表示为点乘的形式。

加权向量

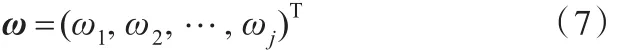
加权规范决策矩阵

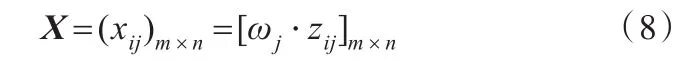
（5）确定正理想解 X+与负理想解 X-。设正理想解 X+的第 j个属性值为，负理想解 X-的第 j个属性值为，则

熵权

（6）计算各评估对象到正负理想解的距离［22］：

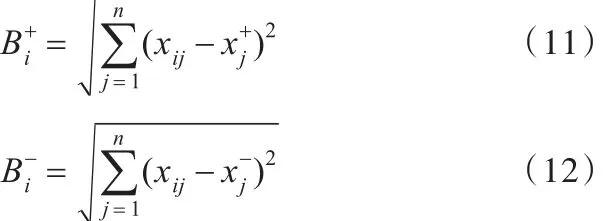
（7）计算相对接近度并排列方案的优劣次序：

根据相对接近度对评估对象进行优劣排序，相对接近度值越大，表明该评估对象的综合评估结果越好；反之，综合评估结果就越差。

2.2 改进熵权TOPSIS法的限寿件风险评估流程

改进熵权TOPSIS法的限寿件风险评估流程见图1。评估流程可分为以下4个阶段：①通过限寿件FMEA方法，确定主要故障模式并对其风险指标进行三角模糊数描述；②建立和规范故障模式三角模糊数决策矩阵；③集成相关专家和工程人员的决策信息计算风险指标的熵权，以改进TOPSIS方法；④利用TOPSIS法对限寿件故障模式进行排序与评估。

图1 改进熵权TOPSIS法的限寿件风险评估流程Fig.1 Risk assessment process of life-limited parts based on improved entropy TOPSIS method

3 实例计算及分析

以CFM56-5B高涵道比涡轮风扇发动机的限寿件为例，针对5种典型故障模式（断裂、疲劳、变形、裂纹、颤振）进行计算分析，应用改进熵权TOPSIS方法对限寿件故障模式进行风险评估。

限寿件风险指标三角模糊数描述（S、O、D）见表4。表4中，传统方法对故障模式严重度的描述用S′表示，发生频度用O′表示，被检测难易度用D′表示。

表4 限寿件风险指标三角模糊数描述Tab.4 Triangular fuzzy number of risk indicators of life-limited parts

首先，采用传统FMEA方法计算限寿件风险优先数，对限寿件的5种故障模式进行排序：

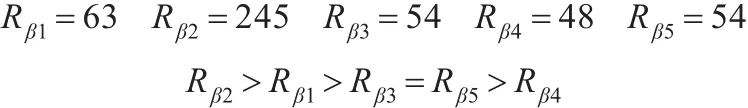
其次，釆用模糊TOPSIS法对故障模式进行评估。限寿件基于故障模式严重度、发生频度和被检测难易度的决策矩阵

根据式（1）将决策矩阵Y转化为规范决策矩阵Z：

根据5位专家和工程人员提供的限寿件风险指标 S、O、D决策信息，可得到矩阵 E=(eij)5×3，即

根据式（2）对矩阵E进行标准化处理可得到矩阵 F=(fij)5×3，根据式（3）计算 gij可得到矩阵G=(gij)5×3，即

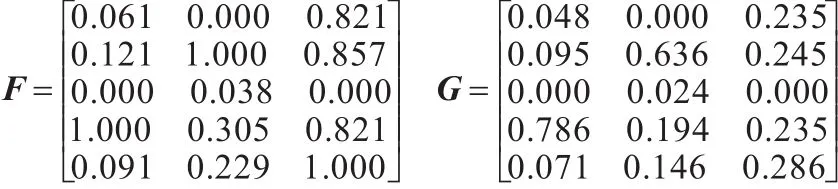
利用信息熵算法计算各风险指标的熵权，作为属性权重ω，根据式（4）～式（6）计算可得

ω =(ω1ω2ω3)Τ=(0.501 0.367 0.132)Τ

根据式（8）确定加权规范决策矩阵 X=ωZ，即

根据式（9）、式（10）确定正负理想解：

X+={(0.047 0.118 0.185)(0.060 0.084 0.059)(0.067 0.093 0.065)}

X-={(0.026 0.051 0.037)(0.040 0.051 0.030)(0.034 0.040 0.022)}

根据式（11）、式（12）计算到正、负理想解的欧氏距离：

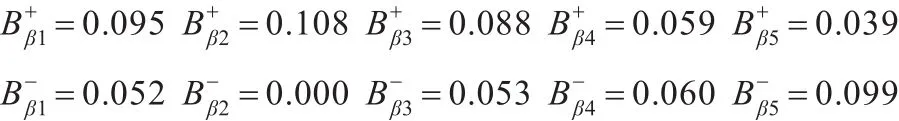
根据式（13）计算各评估对象的相对接近度：

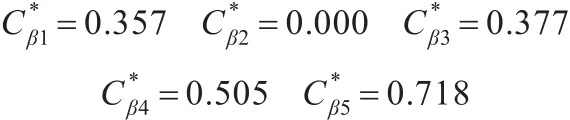
故障模式基于改进熵权TOPSIS法排序如下：

通过改进熵权TOPSIS法对限寿件进行评估，可以实现故障模式的精确排序。限寿件颤振故障尽管不容易被检测出，但是其严重度较小，发生频率也较低，使得其居于故障模式评估顺序的最前端，表明其对限寿件整体运行影响最小。限寿件疲劳故障不仅会造成发动机危害性后果而且很难被检出，故障发生较为频繁，故居于故障模式评估排序的最末端，表明其对限寿件整体运行危害最大。

限寿件基于改进熵权TOPSIS法、危害性矩阵法和传统风险优先数法的评估结果见图2。改进熵权TOPSIS法风险排序结果与危害性矩阵法结果相同，但通过定量计算，该方法的评估结果比危害性矩阵作图法的结果更精确，也比危害性矩阵作图法分析效率更高。改进熵权TOPSIS法对3个风险指标进行模糊化处理，并引入熵权作为属性权重，较传统风险优先数法更准确直观地反映工程实际，评估结果更加客观合理。传统风险优先数风险评估中，限寿件两种故障模式变形和颤振的评估值相等，无法进行排序，而改进熵权TOPSIS法克服了传统风险优先数法当RPN值相等时各故障模式风险难以比较的不足，能够精确排列出5种故障模式的顺序。

图2 限寿件故障模式评估Fig.2 Failure mode assessment of life-limited parts

4 结语

（1）用模糊理论将专家对限寿件风险指标严重度、发生频度和被检测难易度的定性评估信息与模糊数建立联系，将具有一定模糊性的不确定的评估结果转化为确定的三角模糊数，通过计算得出模糊评估，提高了限寿件风险评估的准确性和可信度。

（2）以航空发动机限寿件典型故障模式为评估对象，运用改进熵权TOPSIS法进行风险评估，建立和规范三角模糊决策矩阵，用熵权法确定属性权重修正决策矩阵，确定正负理想解，计算各评估方案与正负理想解的欧氏距离并排序，根据相对接近度对评估对象进行排序与评估。

（3）在限寿件故障数据较少且为小子样的情况下，集成相关专家和工程人员的决策信息来计算风险指标熵权，并作为加权向量对规范决策矩阵进行修正。应用实例计算与分析，改进熵权TOPSIS法的评估结果与危害性矩阵的评估结果相同，证明了该评估方法的可行性和有效性。

［1］ 中国民用航空局.CCAR-33R2 航空发动机适航规定［S］.北京：中国民用航空局，2011.Civil Aviation Administration of China.CCAR-33R2，China Civil Aviation Regulations［S］.Beijing：CAAC，2011.

［2］ US Department of Transportation，Federal Aviation Ad⁃ministration.CFR 14 Part 33，Airworthiness Stan⁃dards：Aircraft Engines［S］.Washington D C：FAA，2013.

［3］ European Aviation Safety Agency.Certification Specifi⁃cation for Engine（CS-E）［S］.Cologne：EASA，2010.

［4］ US Department of Transportation，Federal Aviation Ad⁃ministration.Advisory Circular 33.70-1，Guidance Ma⁃terial for Aircraft Engine Life-limited Parts Require⁃ments［S］.Washington，D C：FAA，AC 33.70-1，2009.

［5］ US Department of Transportation，Federal Aviation Ad⁃ministration.Advisory Circular 33.75-1A，Guidance Material for 14 CFR 33.75，Safety Analysis［S］.Wash⁃ington D C：AC 33.75-1A，2007.

［6］ 曹茂国，钱金善.航空发动机可靠性分析技术FMEA/FMECA［J］.航空发动机，1995（4）：32-39.CAO Maoguo，QIAN Jinshan.Reliability Analysis Tech⁃nology of Aeroegine FMEA/FMECA［J］.Aeroegine，1995（4）：32-39.

［7］ 火建卫，李雅琳，薛海红.危害性矩阵分析中故障模式影响概率的确定方法［J］.航空工程进展，2015，6（2）：228-232.HUO Jianwei，LI Yalin，XUE Haihong.Determination Method of Failure Effect Probability in Criticality Ma⁃trix Analysis［J］.Advances in Aeronautical Science and Engineering，2015，6（2）：228-232.

［8］ 王锦妮，火建卫.定量危害性矩阵分析方法研究［J］.航空工程进展，2016，7（1）：70-77.WANG Jinni，HUO Jianwei.Research on Quantitative Criticality Matrix Analysis Method［J］.Advances in Aeronautical Science and Engineering，2016，7（1）：70-77.

［9］ 陈政平，付桂翠，赵幼虎.改进的风险优先数（RPN）分析方法［J］.北京航空航天大学学报，2011，37（11）：1395-1399.CHEN Zhengping，FU Guicui，ZHAO Youhu.Im⁃proved Analysis Method of Risk Priority Number［J］.Journal of Beijing University of Aeronautics and Astro⁃nautics，2011，37（11）：1395-1399.

［10］ 纪江明.我国城市公共服务满意度指数研究——基于熵权TOPSIS法的分析［J］.国家行政学院学报，2013（2）：38-46.JI Jiangming.Study on Urban Public Service Satisfac⁃tion Index in China—Analysis Based on Entropy TOPSIS Method［J］.Journal of Chinese Academy of Governance，2013（2）：38-46.

［11］ 中国人民解放军总装备部.GJB/Z 1391-2006故障模式、影响及危害性分析指南［S］.北京：总装备部军标出版发行部，2006.General Armament Department of the Chinese Peo⁃ple’s Liberation Army.GJB/Z 1391-2006 Guide to Failure Mode，Effects and Criticality Analysis［S］.Beijing：Military Standard Publication Distribution Department of General Armament Department，2006.

［12］ 苗雨奇.FMECA在航空发动机研制工作中的应用［J］.航空发动机，2000（3）：56-60.MIAO Yuqi.Application of FMECA in Aeroengine Development Work［J］.Aeroengine，2000（3）：56-60.

［13］ 沈颂华，李瑛，康锐.航空电源系统FMEA自动化技术研究［J］.北京航空航天大学学报，1997，23（6）：805-809.SHEN Songhua，LI Ying，KANG Rui.Study of FMEA Automation Technique for Airborne Power System［J］.Journal of Beijing University of Aeronautics and Astronautics，1997，23（6）：805-809.

［14］ 冯蕴雯，姚雄华，薛小锋，等.民机舱门安全性分析方法研究［J］.西北工业大学学报，2013，31（5）：803-809.FENG Yunwen，YAO Xionghua，XUE Xiaofeng，et al.An Effective Safety Analysis Method of Civil Aircraft Cabin Door［J］.Journal of Northwestern Polytechni⁃cal University，2013，31（5）：803-809.

［15］ 张大钢，于天民，陈晓彤.与产品设计相融合的故障模式影响分析（FMEA）技术应用研究［J］.质量与可靠性，2014，170（2）：14-18.ZHANG Dagang，YU Tianmin，CHEN Xiaotong.Technology Application Research for Failure Mode and Effect Analysis（FMEA）Integrated with Product Design［J］.Quality and Reliability，2014，170（2）：14-18.

［16］ 宋彪，王旭，张欢.基于FMEA的飞机燃油箱防火安全性分析［J］.中国民航大学学报，2013，31（5）：14-18.SONG Biao，WANG Xu，ZHANG Huan.Aircraft Fu⁃el Tank Fire Safety Analysis Based on FMEA［J］.Journal of Civil Aviation University of China，2013，31（5）：14-18.

［17］ 徐泽水.对方案有偏好的三角模糊数型多属性决策方法研究［J］.系统工程与电子技术，2002，24（8）：9-12.XU Zeshui.Study on Method for Triangular Fuzzy Mumber-based Multi-attribute Decision Making with Preference Information on Alternatives［J］.Systems Engineering and Electronics，2002，24（8）：9-12.

［18］ 张永利，计文平，刘楠楠.基于熵权-TOPSIS-灰色关联的目标威胁评估研究［J］.现代防御技术，2016，44（1）：72-78.ZHANG Yongli，JI Wenping，LIU Nannan.Target Threat Evaluation Based on Entropy Weight-TOP⁃SIS-Grey Correlation［J］.Modern Defence Technolo⁃gy，2016，44（1）：72-78.

［19］ 张传平，高伟.基于熵权-灰色关联-TOPSIS方法的山东省低碳经济综合评价［J］.科技管理研究，2014，34（17）：37-42.ZHANG Chuanping，GAO Wei.Comprehensive Eval⁃uation of Shandong Low-carbon Economy Based on Entropy Weight and Grey Correlation and TOPSIS［J］.Science and Technology Management Research，2014，34（17）：37-42.

［20］ 雷勋平，ROBIN Qiu，刘勇.基于熵权TOPSIS模型的区域土地利用绩效评价及障碍因子诊断［J］.农业工程学报，2016，32（13）：243-253.LEI Xunping，ROBIN Qiu，LIU Yong.Evaluation of Regional Land Use Performance Based on Entropy TOPSIS Model and Diagnosis of Its Obstacle Factors［J］.Transactions of the Chinese Society of Agricultur⁃al Engineering，2016，32（13）：243-253.

［21］ 黄智力.基于三角模糊数型群体多属性决策法研究［D］.厦门：厦门大学，2009.HUANG Zhili.Research on Multi-attribute Deci⁃sion-making Method Based on Triangular Fuzzy Num⁃ber［D］.Xiamen：Xiamen University，2009.

［22］ 黄智力，罗键.基于群体理想解的三角模糊数群体多属性决策［J］.厦门大学学报（自然科学版），2011，50（5）：817-822.HUANG Zhili，LUO Jian.Method for Triangular Fuzzy Number Multi-attribute Group Decision-mak⁃ing Based on Group’s Ideal Solution［J］.Journal of Xiamen University（Natural Science），2011，50（5）：817-822.