一种三自由度可重构并联机构优化设计及性能分析

邹 琦 曲海波 郭 盛

北京交通大学机械与电子控制工程学院，北京，100044

0 引言

可重构并联机构兼具并联机构刚度大、精度高的特征和可重构设计针对不同任务的适应性较强的特点。可重构并联机构主要分为两类，一种可重构并联机构利用奇异位置重构，另一种通过改变机构的拓扑结构，进而改变机构的自由度，即变胞并联机构［1-3］。本文所关注的是一种由于增加了多余的运动关节，使机架可重构或改变机构装配关系的可重构并联机构。这类机构的目标并不是改变动平台的自由度，而是提升机构的性能。

可重构并联机构优点突出，然而在航空航天等工业场合应用不多［4］。已有的机构大多比较昂贵、反应速度较慢，导致利用率相当有限。为此，国内外学者对可重构并联机构做了许多研究。PLITEA等［5］设计的6自由度可重构并联机构——Recrob 3-PRRS机构，在不同的条件下该机构可成为2/3/4/5自由度可重构并联机构，结构简单且易于控制。SRIVATSAN等［6］研制了3自由度可重构并联机构——MaPaMan（the Madras Parallel Ma⁃nipulator），该机构含有3个相同的支链，重构成不同的构型时，其自由度数目及类型各不相同。XI等［7］提出了一种在保持驱动效率时利用不同的拓扑结构增强机器人的静力学和刚度特性的机构。SON等［8］设计了一种多自由度桌面式可重构机床，该机床的优势是有2个摆动式的拱形轨道模块使其结构更加灵活，适应性更强。CARBON⁃ARI等［9］研制了一类源于3-CPU机构的可重构模块并联机器人，其设计的锁紧系统允许一个旋转副有选择地与另一个旋转副固定，从而使机构重构成具有不同机动性的并联机构。ZHANG等［10］设计的6自由度可重构并联机构可以重构为3/4/5自由度并联机构。COPPOLA等［11］设计了一种应用于可持续制造领域的6自由度可重构混合并联机构——ReSI-Bot。上述机构的可重构过程几乎都是同时改变所有支链，而关于对称地改变部分支链情形的研究较少。

本文设计了一款新型的具有2T1R（2个移动自由度、1个转动自由度）的机架可重构并联机构——2-PRRR+RRR机构，通过对称改变其中2条支链进行重构。

1 运动学分析

本文提出的2-PRRR+RRR机构构型和机构简图见图1。机构的移动副可由圆弧导轨MN实现，其中O为圆弧弧心，对应的圆心角为120°。点O与圆弧MN固定，AiBiCi为3条支链，AiBi与BiCi分别对应相等（i=1，2，3），∆C1C2C3为动平台，G点为动平台几何中心，点 A2和 A3可以在圆弧MN上移动。该机构包括10个杆件和11个运动副（9个转动副和2个移动副），由修正后的Grübler-Kutzbach公式［12］有

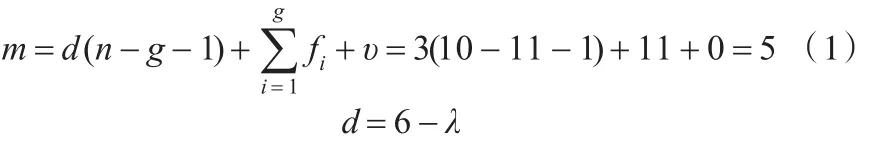
式中，m为机构的自由度；d为机构的阶数；λ为机构的公共约束数目，一般地，空间机构的阶数是6，平面机构的阶数是3；n为活动构件数；g为运动副数目；fi为第i个运动副所具有的自由度数目；υ为机构的冗余约束数。

图12 -PRRR+RRR机构Fig.1 2-PRRR+RRR mechanism

由式（1）计算出机构的自由度是5，则相应的独立驱动数是5。该机构属于平面机构，动平台的自由度为3，分别是沿X轴、沿Y轴的移动自由度和绕Z轴的转动自由度。这里仅仅采用3个电机驱动，分别安装于转动副 A1、A2和 A3处，且A2、A3处电机输出分别包含两部分，一部分直接驱动转动副，另一部分利用离合器与外齿轮传动系统实现A2、A3处的移动运动（该离合器使得机构在任意位置均可安全锁紧）。这样，减少了电机及传动系统的数目，也降低了控制系统的难度。另外，可重构机构可以通过对称地改变A2、A3点在圆弧导轨中的位置而产生无穷多的对称位置，易于控制。

1.1 逆运动学分析

建立图1b所示的坐标系。A1与坐标系的原点O重合，X轴水平向右，Y轴竖直向上。杆件AiBi长度为ai，杆件 BiCi长度为bi，圆弧 MN 半径为R，∆C1C2C3边长为h，AiBi与X轴正方向夹角为 θi，AiBi和 BiCi的夹角为 φi，C1C2与X轴夹角为φ，A1A2和X轴夹角为α，A1A3和X轴夹角为 β，A1M 与Y轴重合，A1N与X轴夹角为-30°。

已知C1点的坐标（XC1，YC1）、φ、α和 β，求解 θi（i=1，2，3）。以支链 A1B1C1为例，应用下面的矢量方程求解：

联立方程并写成坐标形式，有

将式（3）两边分别平方后相加，即可消去φ1，得到关于 sin θ1和 cosθ1的方程，用三角万能公式替代，得到一元二次方程：

求解可得

由结果可知，θ1解的个数可能有0、1或2个，对应支链 A1B1C1分别是无解、有1个或2个位置。用相同的方法，可求解另外2条支链。3条支链组合，则机构最多有8个可能的解，对应不同的α和 β，结果亦然。

1.2 正运动学分析

正运动学研究是由机构的驱动关节坐标确定末端操作器的位姿，具体到该机构则是由输入变量 θi（i=1，2，3）、α 和 β 求解动平台的位姿参量XC1、YC1、φ 。

式（3）两边分别平方后相加，得到关于 XC1、的二元二次方程：

同理，由另外2条支链可得

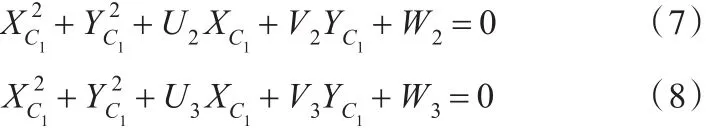
式中，Ui、Vi、Wi是θi、φ、α、β的函数。

联立式（6）～式（8）并消去平方项，即可求解出XC1和YC1，代入式（6）中，得到关于 sin φ 和cosφ的四次方程，用三角万能公式替代可得1个一元八次方程，即给定机构的输入参数，最多会有8个可能的位置。

1.3 雅可比矩阵

为了2-PRRR+RRR机构的杆件优化设计，有必要首先推导出该机构的雅可比矩阵，这里选用微分变换法求解雅可比矩阵。由点Ci与点G(XG,YG)的位置关系和bi杆的约束方程，有

展开并对时间求导得到

其中，分别为Bi点的横坐标和纵坐标。为便于表达，将式（10）整理成以 X˙G、Y˙G、φ˙及 θ˙i为未知量的方程，系数 JXij、Jqij（i，j=1，2，3）组成了雅可比矩阵中的元素，即

则雅可比矩阵表示为

2 优化设计

2.1 优化设计目标

为了使机构获得更好的性能，通常以机构的灵巧度和工作空间等作为衡量指标。

灵巧度衡量的是机构输入速度与输出速度关系的精度，灵巧度指标可以检测机构是否处于奇异位置或接近奇异位置，表征灵巧度的指标有条件数和可操作度［13］。条件数定义如下：

其中，W 为加权矩阵，则有1≤κ(J)≤∞。取条件数的倒数为局部条件指标 ILCI，则0≤ILCI≤1，ILCI越接近1的位姿表明此处机构的运动性能越好，因此在工作空间V上的全局条件指标IGCI为

且 IGCI越接近1，机构的全局运动性能越好。为了体现条件数的整体分布情况，引入以下函数：

式中，ε为表征在整个可达工作空间内条件数的波动程度。

综合这两个指标，得到

式中，ξ、τi（i=1，2，3）分别是 ε、ξ、IGCI和工作空间的权重系数。

f函数的数值越小，ILCI的波动程度越小，全局条件数和机构的可达工作空间越大，因此以f作为目标函数，可同时考虑机构的灵巧度、波动程度及工作空间，得到较好的结果。

2.2 优化计算

遗传算法是借鉴生物界自然选择和自然遗传机制发展起来的随机全局搜索和优化的算法［14］，其运算过程不受所求解目标函数相关理论的影响，由此求出优化解，运算速度快而且结果比较可靠。本文采用遗传算法进行优化。

假设3条支链杆件对应相等，以2.1节中计算的f为遗传算法的适应度函数，进行基于一种十分通用的数值计算方法——蒙特卡罗法的杆件优化。模型参数中，α和 β的值分别是 π 9和4π/9 ，ξ和 τi（i=1，2，3）取值分别为 14、10、1和1/300，初始种群大小是50，选择算子选择随机均匀分布，交叉概率为0.8，终止条件的停止代数为50，停滞代数为50，设计变量共4个，根据设计要求，自变量（单位mm）的取值范围为

适应度函数取为f时，优化后的变量取值分别为R=100 mm，h=25 mm，ai=76 mm，bi=79 mm。由图2可知，最佳适应度值为0.432 936，平均值为0.447 185。此外，随着代数增多，最佳适应度函数值和平均适应度函数值逐渐接近，表明适应度函数已经收敛到优化解。

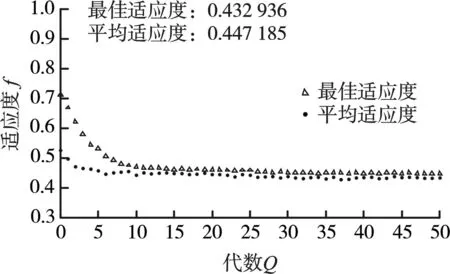
图2 最佳适应度与平均适应度Fig.2 Best fitness and mean fitness

3 工作空间

采用一种通用的离散边界搜索算法计算机构的工作空间，该算法直接依据运动学逆解和几何约束条件，因此计算过程较简单，计算时间可以显著缩短。具体的计算和绘图步骤如下：

（1）按照设计要求，分析并设计出该机构各个维度的参数。该机构属于平面机构，所以应初步确定 Xmin、Xmax、Ymin、Ymax、φmin和 φmax的值。

（2）确定由机构杆件尺寸及运动副约束（主要指转动副转角限制）组成的几何边界条件，动平台处于初始位置，为方便计算，初始位置设计为各个边界的最小值所表示的位置。

（3）从动平台的初始位置开始，分别设计出沿X轴、沿Y轴和绕Z轴的步距。一般地，为了得到更加精准的计算结果，步距应越小越好。在该案例中为计算定姿态的工作空间，沿X轴和Y轴的步距均为0.1 mm，φ设置为定值0°。

（4）增加步距，动平台从初始位置或前一位置逐渐移动，由前面的分析求解该位置对应的运动学逆解。

（5）应用步骤（2）得到的机构应满足的约束条件来检验动平台的位姿是否在约束条件的边界内部，若在边界内部，则计数器（初始值为0）加1，然后返回步骤（4）；否则直接返回到步骤（4）。

（6）几何边界内的值已经被遍历，动平台到达工作空间的边界，算法终止，于是可以绘制出机构的工作空间。

由该算法绘制机构的定姿态工作空间（φ=0），杆件尺寸取优化后的数值。不同位置下机构的工作空间见图3。

图3 机构的工作空间Fig.3 Workspaces of the mechanism

由图3可知，案例中的3个工作空间都是对称图形，对称轴数量分别为1、3、1。机构3条支链杆件尺寸分别对应相同时，机构的定姿态工作空间是可变的、对称的。当α和 β在给定范围内（-π/6≤α＜β≤π/2）取任意值时，机构恒具有对称性，对称轴的斜率为 tan((α+β)/2)。

4 性能分析

4.1 规避奇异位形区域

由1.3节求解出的雅可比矩阵能够对机构的奇异性进行分析。该2-PRRR+RRR并联机构的一个特例是平面3-RRR并联机构（当满足β-α=π/3时），文献［15］中关于平面3-RRR并联机构奇异位形的分析对该机构同样适用。

（1）逆运动学奇异。当机构的任一支链完全伸展或者折叠时发生逆运动学奇异，即φi=0或π（i=1，2，3），当机构中分别有1、2或者全部支链出现这种情况时，并联机构相应地失去1、2或3个自由度。

（2）正运动学奇异。当 B1C1、B2C2和 B3C3交于一点（图4a）或者互相平行（图4b）时，机构发生正运动学奇异。由于正运动学奇异的所有可能性不易直接罗列，这里仅仅给出了图4的2种奇异位形。

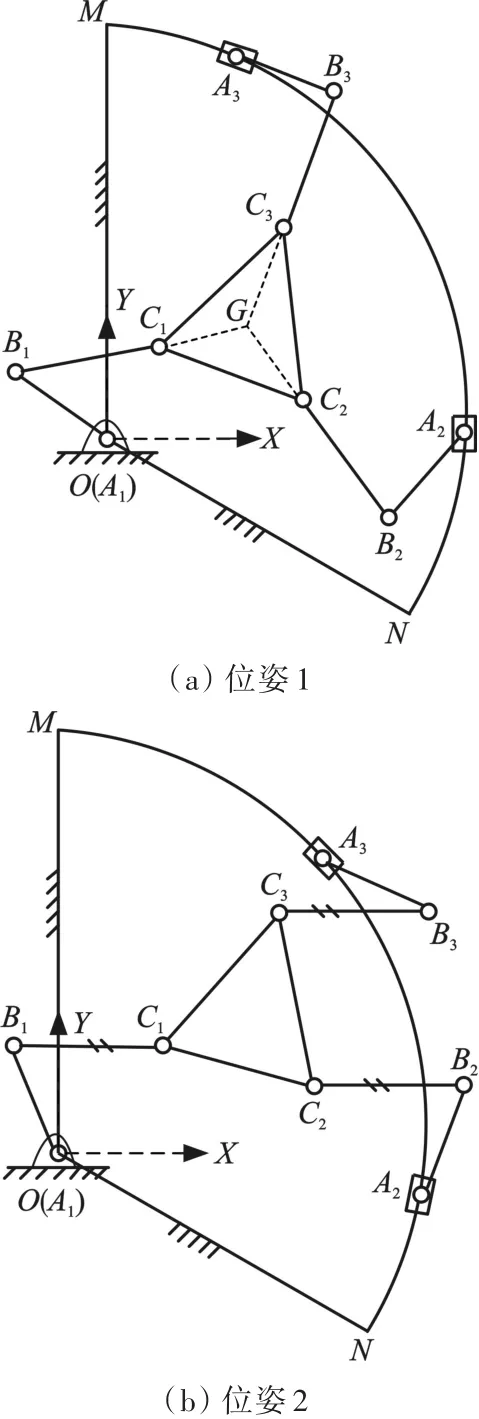
图4 正运动学奇异位姿Fig.4 Singular configurations of forward kinematic

（3）逆运动学奇异和正运动学奇异同时发生的情况称为组合奇异，组合奇异受机构的尺寸和位姿的影响，因此设计时应避免会引起奇异的杆件尺寸关系。

上述奇异位形及其附近区域会对机构的运作及精确控制造成不利影响，而 A2和 A3处的移动副可以解决这一问题。当机构陷入奇异位形或临近奇异位形区域时，A2和A3处的离合器接合，在电机的驱动下，齿轮副开始运转，从而带动A2点或 A3点沿圆弧轨道移动，此时θ2或θ3也在变化，双重的变动使机构脱离奇异位形或奇异位形区域。然后，离合器分离，移动副的动力断开且A2或A3点被锁紧，机构可以重新正常作业。

当α和 β确定后，轨迹规划中并联机构需要经过奇异位形的情况下，可以选择按照既定方案运动，在奇异位形附近，更改α或 β的值，以非奇异的位形实现该轨迹。这一特性体现了该并联机构较强的运动能力，同时也表明该可重构并联机构优于普通并联机构。

4.2 转动性能

如前所述，该可重构并联机构和平面3-RRR并联机构均属于平面机构，具有2个移动自由度和1个转动自由度。并联机构在不同位置下的转动性能对其应用影响较大，因此有必要讨论该机构的转动能力。此处以动平台上绕C1点的φc=φmax-φmin值来表征机构的转动性能。机构的杆件尺寸取值为R=130 mm，h=10 mm，ai=20 mm，bi=60 mm，i=1、2、3。忽略机构中间关节的转角范围，依据1.1节中的位置逆解分别计算2种机构在不同位置下的转动能力，图5a和图5b所示分别表示3-RRR并联机构和2-PRRR+RRR机构在不同位置的转动能力，图中每个位置的转动能力为封闭几何体的上界，即沿Z轴的最大值。对比可知：①相比平面3-RRR并联机构，所设计机构可达工作空间明显增大；②由计算可知，平面3-RRR并联机构转动能力最大值为3.665 2，且图5a几何体上平面较尖，表明只有小部分的位置能达到这种姿态范围，而该机构大部分位置都可以达到6.283的转动能力，因此图5b几何体的上平面接近水平；③同一位置点时，图5b比图5a的Z轴值大，表明在可达工作空间的同一位置，该机构能达到更大的转角范围。

4.3 容错工作空间

图5 转动性能Fig.5 Rotation capability

并联机构的驱动器和关节是故障多发部件，这些故障会对所设计机构的工作能力产生严重影响，还有可能造成较大的经济损失，随着机器人应用的领域越来越广阔，这些问题得到了广泛的关注。以下分两种情况进行讨论。

（1）关节 A1故障，此时 A1处关节被锁紧，杆件 A1B1固定。假设θ1=π/3，C1点的轨迹在以B1(a cosπ/3,a sin π/3)为圆心、 ||B1C1为半径的圆上。

（2）关节 B1故障，杆件 A1B1和 B1C1合为一个构件。如给定φ1=3π/2，A1B1C1形成一个三角形，由余弦定理可知，| A1C1|=，显然，C1点的轨迹在以A1点为圆心以 | A1C1|为半径的圆上。

同样地，依据1.1节中的运动学逆解，分析2个并联机构在A1点和B1点故障时G点的工作空间，分别见图6、图7。由图6和图7可知：①2个案例中3-RRR平面并联机构G点位置均为一小段属于右半部分的圆弧，而可重构并联机构G点能达到的位置为几个没有交集的圆，并且前者轨迹包含在后者中；②可重构并联机构G点位置在案例1中为5个圆和1段圆弧，案例2中为5个圆和3段圆弧，表明案例2下G点的工作空间更大，然而各圆或圆弧之间相互没有交集，所以在不同位置故障时，G点运动受限，最大轨迹为1个圆；③案例1、2中，无论在何种位置故障，后者的工作空间总大于前者。

图6 案例1的工作空间Fig.6 Workspace of case 1

图7 案例2的工作空间Fig.7 Workspace of case 2

5 结论

（1）设计了一种机架可重构并联机构——2-PRRR+RRR机构，机架重构过程是利用离合器系统与齿轮传动系统相配合来实现1个驱动输入2个运动输出，且机构可同时对称地改变可重构的2条支链，机构运动灵活、控制相对简单。

（2）在运动学建模的基础上，以同时考虑全局灵巧度及离散程度和工作空间的函数为优化目标，计算出了机构杆件尺寸，分析了其可达工作空间，验证了提出的机构性能更加优良。

（3）由位置奇异分析可知，该机构可规避奇异位形区域，便于轨迹规划，通过转动能力分析表明该机构转动性能较强，借助于机架重构功能，当部分关节发生故障时动平台能达到比3-RRR机构更多的位姿，可靠性较高。

（4）如前所述的优点，该机构可用于物料拾取，后续也将探索配合具有可动的工件平台组成4/5/6自由度的机构，扩大该机构的应用范围。

［1］ 叶伟，方跃法，郭盛，等.基于运动限定机构的可重构并联机构设计［J］.机械工程学报，2015（13）：137-143.YE Wei，FANG Yuefa，GUO Sheng，et al.Design of Reconfigurable Parallel Mechanisms with Discontinu⁃ously Movable Mechanism［J］.Journal of Mechanical Engineering，2015（13）：137-143.

［2］ ZLATANOV D，BONEV I A，GOSSELIN C M.Con⁃straint Singularities of Parallel Mechanisms［C］//IEEE International Conference on Robotics and Automation.Washington D C，2002：496-503.

［3］ 戴建生，丁希仑，邹慧君.变胞原理和变胞机构类型［J］.机械工程学报，2005，41（6）：7-12.DAI Jiansheng，DING Xilun，ZOU Huijun.Fundamet⁃als and Categorization of Metamorphic Mechanisms［J］.Journal of Mechanical Engineering，2005，41（6）：7-12.

［4］ BI Z M，WANG L.Optimal Design of Reconfigurable Parallel Machining Systems［J］.Robotics and Comput⁃er-Integrated Manufacturing，2009，25（6）：951-961.

［5］ PLITEA N，LESE D，PISLA D，et al.Structural Design and Kinematics of a New Parallel Reconfigurable Robot［J］.Robotics and Computer-Integrated Manufacturing，2013，29（1）：219-235.

［6］ SRIVATSAN R A，BANDYOPADHYAY S.On the Po⁃sition Kinematic Analysis of Mapaman：a Reconfigu⁃rable Three-degrees-of-freedom Spatial Parallel Manip⁃ulator［J］.Mechanism and Machine Theory，2013，62（4）：150-165.

［7］ XI F，XU F，XIONG G.Design and Analysis of a Re⁃configurable Parallel Robot［J］.Mechanism and Ma⁃chine Theory，2006，41（2）：191-211.

［8］ SON H，CHOI H J，PARK H W.Design and Dynamic Analysis of an Arch-type Desktop Reconfigurable Ma⁃chine［J］.International Journal of Machine Tools and Manufature，2010，50（6）：575-584.

［9］ CARBONARI L，CALLEGARI M，PALMIERI G，et al.A New Class of Reconfigurable Parallel Kinematic Ma⁃chines［J］.Mechanism and Machine Theory，2014，79：173-183.

［10］ ZHANG K，EMMANOUIL E，FANG Y，et al.Typechangeable Kinematic Pair Evolved Reconfigurable Parallel Mechanisms［C］//ASME/IFToMM Interna⁃tional Conference on Reconfigurable Mechanisms and Robots.Tianjin：Springer，2012：309-319.

［11］ COPPOLA G，ZHANG D，LIU K F.A 6-DOF Recon⁃figurable Hybrid Parallel Manipulator［J］.Robotics and Computer-Integrated Manufacturing，2014，30（2）：99-106.

［12］ 黄真，孔令富，方跃法.并联机器人机构学理论及控制［M］.北京：机械工业出版社，1997：12.HUANG Zhen，KONG Lingfu，FANG Yuefa.Theory and Control of Parallel Robot Mechanism［M］.Bei⁃jing：China Machine Press，1997：12.

［13］ 金振林，曹舜，高峰.新型机器人肩关节及其运动学 分 析［J］.中 国 机 械 工 程 ，2009，20（14）：1639-1642.JIN Zhenlin，CAO Shun，GAO Feng.Design and Ki⁃nematics Analysis of a Novel Robot Shoulder Joint［J］.China Mechanical Engineering，2009，20（14）：1639-1642.

［14］ 雷英杰，张善文.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2014.LEI Yingjie，ZHANG Shanwen.MATLAB Genetic Al⁃gorithms and Applications［M］.Xi’an：Xidian Univer⁃sity Press，2014.

［15］ TSAI L W.Robotic Analysis：the Mechanics of Serial and Parallel Manipulators［M］.Hoboken：John Wiley&Sons，1999.