基于镜面反射的手眼标定方法

张 旭 贾君慧 张 刚

1.上海大学机电工程与自动化学院，上海，200072 2.华中科技大学无锡研究院机器人技术中心，无锡，214147

0 引言

在机器人视觉控制领域里，手眼视觉系统是实现主动视觉的主要设备，把视觉传感器获取的位置信息转换到工具坐标系下需要求出视觉传感器坐标系相对于机器人工具坐标系的位姿关系，即机器人的手眼关系。

传统的机器人手眼关系标定方法［1］根据参照物的几何特征，利用几何约束把所有待求变量一起求出。XU等［2］基于TCP提出了一种将标准球作为标定物的标定方法，用3D扫描仪扫描标准球拟合出球心，在计算平移矩阵时需要用旋转矩阵的结果，类似于两步法，但操作复杂。LI等［3］提出了一种用标准球标定机器人和扫描仪之间关系的手眼标定方法，但球的拟合误差没有讨论，并且实验设备复杂。杨广林等［4］通过控制机器人做2次平移运动和1次旋转运动，由场景中的2个特征点获得所需的手眼关系，但机器人运动所造成的误差无法避免。程玉立［5］提出了一种在线自动化手眼标定方法，但精度较差。张召瑞等［6］提出了一种融合旋转平移矩阵对约束信息进行求解的方法，但操作繁琐。

手眼标定的难点在于“眼”看不到“手”，即相机看不到机器人末端执行器。根据镜面反射定律，实物和镜中虚像具有一致性，因此平面镜具有转换相机视场的功能。通过平面镜，组成手眼视觉系统的相机可以看到末端执行器。目前已经有多名学者对相机镜面反射问题进行了研究，RUI等［7］认为在平面镜反射引起的N个虚拟视图之间的刚性运动已知时，可以估计出相机的位姿和平面镜的位置。HESCH等［8］提出，相机通过平面镜拍摄至少有3个相对位置已知的物体时，改变平面镜姿态，可求出物体与相机之间的位姿关系以及平面镜与相机之间的位置信息。

本文针对Eye-on-Hand机器人手眼系统，设计出一种基于平面镜反射的手眼标定系统。由于机器人末端执行器特征较少，因此将连接标定板作为辅助特征。相机拍摄到平面镜中的标定板图像后，根据镜面标定方法来求解相机与标定板之间的位姿关系，通过辅助相机确定末端执行器坐标系和标定板坐标系的转换矩阵，最终确定相机坐标系和机器人末端执行器坐标系的位姿关系，完成手眼标定。

1 手眼标定系统介绍

手眼标定的目的是确定相机坐标系相对于机器人末端执行器坐标系的关系。传统的手眼标定方法［9］是：相机固定在机器人末端，在相机视野范围内放置一块标定板，通过移动机器人，在不同位置获取标定板的图片，通过张正友标定法［10］标定出相机的内外参数；机器人在移动前后的位姿由机器人控制器读取，通过计算获得相机坐标系相对于机器人工具坐标系的位姿。传统标定方法需要机器人和相机同步运动，并且通过机器人参数和相机标定参数耦合求解，标定过程较为繁琐。镜面位姿标定法则只需平面镜连接相机和机器人末端执行器的视场，标定过程不需要机器人本体参数参与。

确定相机坐标系和机器人末端执行器位姿关系的镜面位姿标定方法主要包括如下三步：①以平面镜为桥梁，连接相机和末端执行器；②通过辅助相机求出标定板坐标系和机器人末端执行器之间的转换矩阵；③求解得到相机坐标系和机器人末端执行器之间的位姿关系。末端执行器上特征点较少，不足以估计其位姿，因此在末端执行器吸附标定板，由镜面位姿标定法获得相机坐标系和标定板坐标系的位姿关系。

图1所示为待求解的“手眼”系统，求解过程是：先根据镜面标定方法得出相机坐标系{C}与标定板坐标系{O}之间的相对位姿；再根据坐标系{O}与机器人末端执行器坐标系{E}之间的相对位姿，计算坐标系{C}与坐标系{E}之间的相对位姿；最后由单目相机模拟双目相机完成三维重建。机器人末端执行器是一个圆形吸盘，其坐标系{E}建立在吸盘中心，机器人基坐标系为{B}。

求解过程可分为三步：①相机坐标系与标定板坐标系之间的位姿关系的求解；②标定板坐标系与吸盘坐标系之间的位姿关系的求解；③单目相机模拟双目视觉系统实现三维重建及抓取。

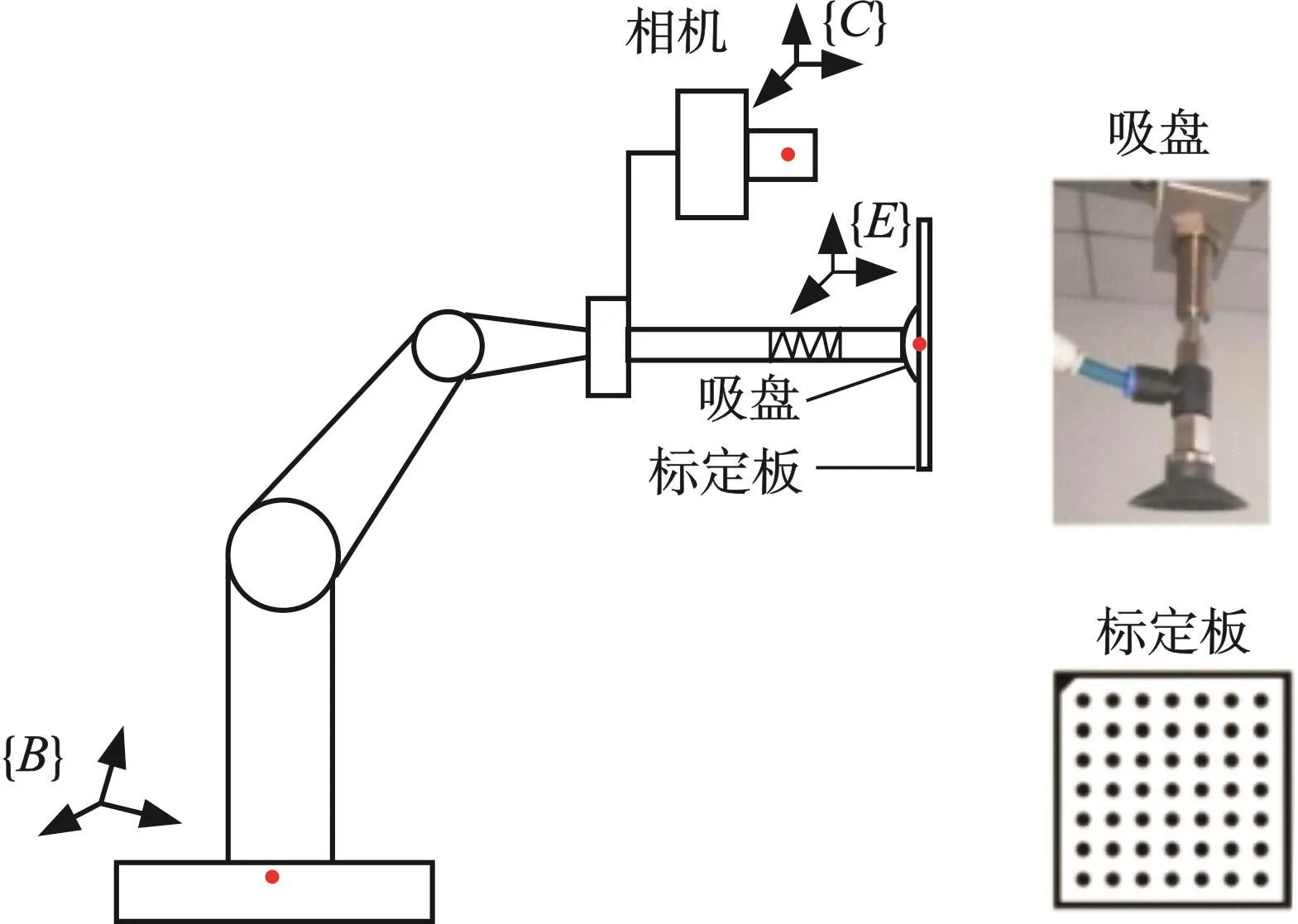
图1 ‘手眼’系统示意图Fig.1 ‘Hand-eye’system diagram

（1）相机坐标系与标定板坐标系之间的位姿关系的求解。如图1所示，相机无法直接拍摄到吸附在吸盘上的标定板。若在合适的位置放置一块平面镜，则相机可以通过平面镜拍摄到标定板在平面镜中的虚像。采用这种方式来标定相机坐标系{C}和标定板坐标系{O}时，要求相机通过平面镜必须能够拍摄到标定板，且只需将镜面位姿改变3次，通过线性算法求解即可获得相机和标定板的位姿关系，同时也可以获得相机的内参数。标定过程中，平面镜的位姿可以随意改变，并且不需要改变机器人的位置和姿态。

（2）标定板坐标系与吸盘坐标系之间的位姿关系的求解。经过镜面位姿求解，可以确定相机坐标系{C}和标定板坐标系{O}之间的旋转矩阵和平移矩阵。一般情况下，标定板坐标系原点与吸盘坐标系的原点并不重合，故还需要经过位姿变换才能求解出相机坐标系{C}和吸盘坐标系{E}之间的位姿关系。由于吸盘和标定板表面重合，因此可以建立图像平面到标定板平面的映射关系，根据此映射关系求解吸盘中心和标定板坐标系的偏移量，从而求解出吸盘坐标系和相机坐标系的位姿关系。

（3）用单目实现三维重建及抓取。在标定完成后，系统就可以实现对物体的抓取，首先通过单目相机模拟双目视觉系统实现对物体的三维重建［11-12］。相机带动机器人平移，在两个位置获取物体的图像，通过两个不同位置的相机构建双目视觉系统。该双目视觉的外参数可以直接从机器人运动参数中读取得到。根据物体在两幅图像中的对应点，利用三角法计算出物体在相机坐标系下的三维信息，经过位姿变换将三维信息变换到机器人末端执行器坐标系下，从而驱动机器人实现对物体的抓取。

2 手眼标定过程

手眼标定过程主要包括两方面：通过镜面标定得出相机坐标系与标定板坐标系之间的位姿关系；通过辅助相机得出标定板坐标系与吸盘坐标系之间的位姿关系。

2.1 镜面标定方法

如图2所示，假设标定板上点p在{O}中的坐标已知，由几何学可知p在{C}中的坐标描述：

式中，Cp′为 p点在平面镜中的虚像 p′在相机坐标系下的平移矩阵；Cp为点 p相对于相机坐标系的平移矩阵；n为平面镜在相机坐标系中的法线，用矩阵描述；L为相机到平面镜的距离；Lp为点 p到平面镜的距离（距离L和距离Lp都是沿着平面镜的法线方向）。

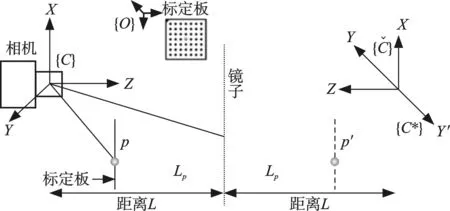
图2 镜面反射示意图Fig.2 Mirror reflection schematic diagram

由点 p在两坐标系中的变换可知：

式中，Op为点 p相对于标定板坐标系的坐标，用矩阵描述；COR为坐标系{O}相对于坐标系{C}的旋转矩阵；CTO为坐标系{O}相对于坐标系{C}的偏移矩阵。

把式（2）、式（3）代入式（1），得

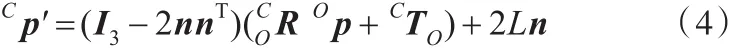
写成齐次坐标的形式：

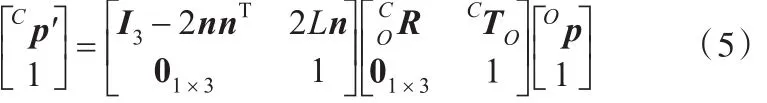
相机获取点Cp在平面镜中的反射点为Cp′，通过这种镜面反射模型来描述该测量系统；,CTO}表示未知的相机到机器人末端执行器的变换，{n,L}为平面镜相对于相机的未知配置参数。由式（5）知，影响平面镜到相机的位姿变换结果的参数是n和L，其中，平面镜法线n有2个自由度，加上标量L，共有3个未知量。

2.2 虚拟相机与真实相机的位姿关系

由图1可知，相机无法直接拍摄到标定板，但借助平面镜，相机就可以拍摄到标定板在平面镜中的虚像。相机拍摄虚拟标定板，通过相机标定得到相机与虚拟标定板之间的旋转矩阵和平移矩阵。如图2所示，{Cˇ}为右手坐标系姿态的虚拟相机坐标系，{C*}为左手坐标系姿态的虚拟相机坐标系。{C*}隐藏在平面镜后，以左手坐标系的姿态获取真实点 p，其Y轴为图2右侧的Y′。两个坐标系的 X轴和Z轴相同，而Y轴沿相反的方向。

简单的齐次变换公式为

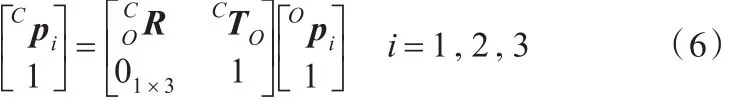
式（5）描述了镜面反射后的齐次变换。为了把式（5）转换成类似式（6）的形式，假设平面镜反射前后的坐标系之间有以下关系：

其中，T表示虚拟标定板在真实相机中的位姿与真实标定板在虚拟相机坐标系中的位姿之间的关系矩阵，为四阶单位阵。

把左手坐标系姿态的虚拟相机转换到右手坐标系，并依据式（5）和式（7）得

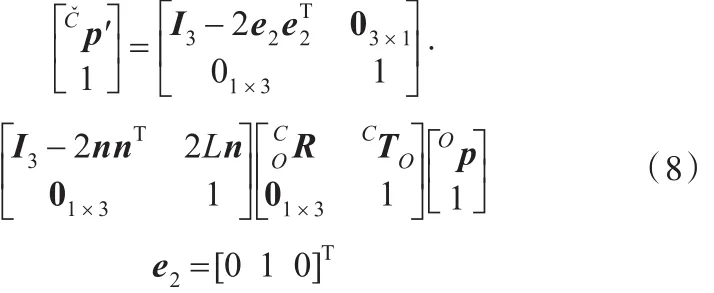
式（8）描述了右手坐标系姿态时的虚拟相机坐标系{Cˇ}与标定板坐标系{O}之间的关系。通过平面镜镜像原理即可得出真实相机坐标系{C}与标定板坐标系{O}之间的关系，该过程需两步：①把右手坐标系姿态的虚拟相机变换为左手坐标系姿态的虚拟相机；②把虚拟相机转换到真实相机坐标系。

式中，A为右手坐标系姿态的虚拟标定板坐标系相对于相机坐标系的旋转矩阵；b为右手坐标系姿态的虚拟标定板坐标系的原点到相机坐标系原点的偏移矩阵。

由式（5）、式（8）可以得到

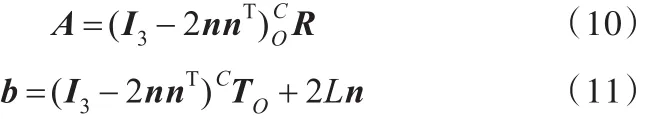
2.3 镜面标定问题求解

将平面镜任意改变3次位姿，便可以获得3个镜面反射图像。对于每一幅镜面反射图像，确定的参数用 Aj、Aj′、bj、bj′描述，j,j′∈{1,2,3} 。定义单位向量 mjj′与 nj和 nj′均垂直，即 nj⋅mjj′=nj′⋅mjj′=0 。根据式（10）可得

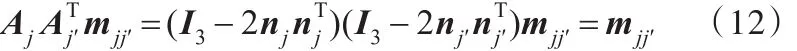
因此，通过计算出的单位特征值所对应的特征向量 m是特殊的正交矩阵，有2个共轭特征值，还有一个特征值为1），再根据特征向量的叉积，可以得到

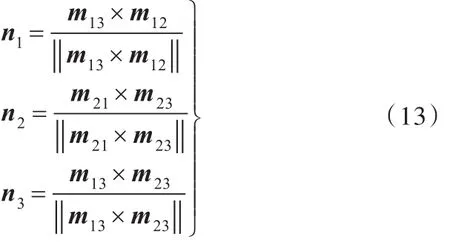
其中，m13为特征值为1时所对应的特征向量；m12为特征值为1时所对应的特征向量；m21为特征值为1时所对应的特征向量；m23为特征值为1时所对应的特征向量。

一旦计算出对应于3个镜面的单位矩阵，旋转矩阵就可以从3组方程中单独地计算出：

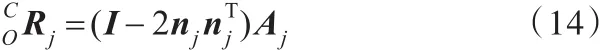
在理想状态下，Rj应该是相等的，但由于噪声的存在，Rj并不相等。为了尽可能减小误差，可以从三组方程中计算COR的平均值。

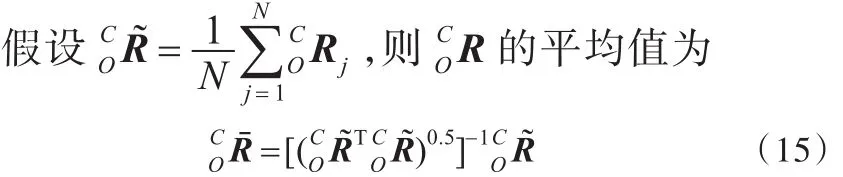
其中，(˜)0.5表示矩阵中元素开方操作。计算得到旋转矩阵和平面镜的法线nj，未知量[CTOL1L2L3]Τ可以根据式（11）构建的线性方程求解，即

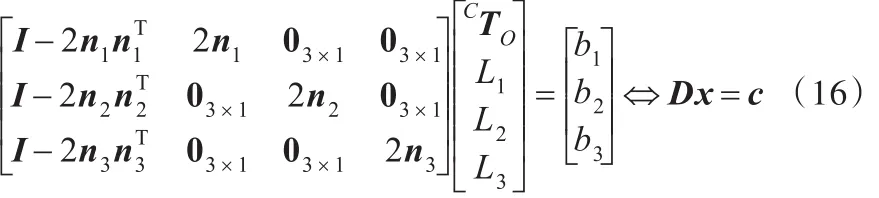
其中，D是9×6的已知系数矩阵；c是9×1的已知矩阵；x是6×1的未知矩阵。 x可以表示为线性x=D†c，其中，D†为 D的广义逆矩阵。至此，不在相机视野范围内的真实标定板与相机的位姿可以通过线性求解得出。

2.4 标定板坐标系和吸盘坐标系的位姿变换

图3中，吸盘圆心与标定板中心点在X、Y方向的偏移值分别由lx、ly表示，lz为标定板厚度。

图3 吸盘中心坐标求解Fig.3 Solution of sucker center coordinate

标定板和吸盘在同一平面上，可以认为标定板坐标系与相机坐标系之间的旋转矩阵和吸盘坐标系与相机坐标系之间的旋转矩阵是一样的，只要求解平移矩阵即可。根据标定板的角点坐标和标定板角点在图像平面的像素坐标的对应性，确定标定板平面到图像平面的映射关系，然后得出坐标系{E}原点在相机坐标系下的坐标CTE，即有

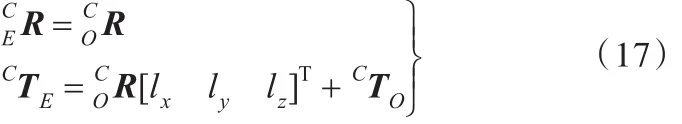
2.5 单目相机模拟双目

相机拍摄物体只能得到物体的二维信息，三维重建时，通常会采用多目相机获取被测物体的多个视角图像，通过三角法重建物体三维信息。本文采用单目相机，通过机器人平移相机构建双目视觉系统，相机在2个不同的位置采集物体图像。2个相机之间的位姿关系可从机器人运动姿态数据中读出。当机器人只有平移运动时，构成双目视觉系统的相机旋转矩阵为单位阵，平移矩阵为机器人的平移量。相应地，基线长度也是机器人的平移量。根据同一目标点在两幅图像中的像素差，可以得到该目标点处对应的视差。根据下式：

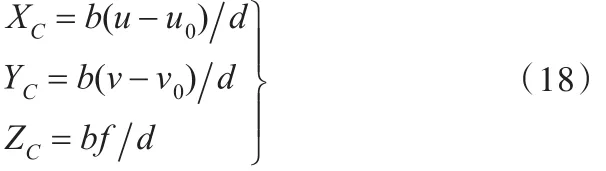
式中，b为基线长度；d为视差；(u0,v0)为图像中心坐标；f为相机的焦距。

通过目标点图像坐标(u,v)到相机坐标(XC,YC,ZC)的转换，获得物体在相机坐标系下的三维信息，并根据求解得到的相机坐标系和机器人末端执行器的位姿关系实现机器人抓取。

3 实验验证

实验采用ABB2600机器人，末端执行器吸盘吸住标定板，将平面镜放在合适的位置，使相机可以通过平面镜拍摄到标定板。采用Basler2500-14gm相机拍摄经过平面镜反射的标定板图像（称为虚拟标定板图像）。采用Halcon标定板，圆直径为2 mm，间距4 mm，圆标志点行数、列数均为7，见图4。

图4 镜面标定实验Fig.4 Mirror calibration experiment

实验中，保持相机和机器人末端执行器不动，平面镜位姿改变3次，通过相机拍摄获取标定板在镜面中的虚像，如图4b所示。通过标定得到平面镜中的虚拟相机与真实标定板的位姿关系或平面镜中的虚拟标定板在相机坐标系下的外参数，包括旋转矩阵和平移矩阵。根据式（10）得出3个平面镜位姿的法线的方向矩阵：

根据平面镜法线的单位矩阵便可求出标定板与相机之间的旋转矩阵，根据式（15）求的均值

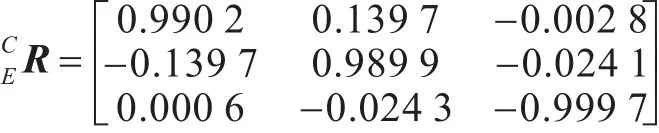
来抑制噪声。

由式（16）、式（17）可以得出标定板与相机之间的平移矩阵以及平面镜与相机的3个距离（单位为mm，下同）：

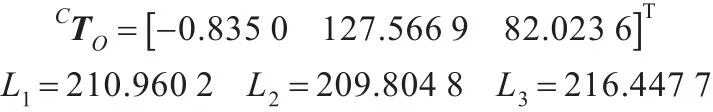
如图5所示，在求解机器人末端执行器和相机坐标系的位姿关系时，根据前面求解得到的标定板坐标系和机器人坐标系的位姿关系，借助辅助相机，通过椭圆检测确定吸盘的中心，得到吸盘中心点O1的像素坐标，然后根据标定板4个角A、B、C、D的像素坐标确定标定板的中心点O2的像素坐标。标定板4个角的像素坐标分别为A（519，855）、B（1 389，924）、C（666，1 178）、D（1 439，1 240），计算得出标定板中心点O2的像素坐标O2（1 003.25，1 049.25）。根据拟合椭圆得到吸盘中心点 O1的像素坐标（996.53，1 059.17），此时可计算得出吸盘中心点O1与标定板中心点O2的像素偏移值（6.71，-9.92）。然后求解标定板平面到图像平面的映射关系，可以确定吸盘圆心相对于标定板中心的偏移量。根据A、B、C、D 4点在标定板上的坐标（0，0）、（63，0）、（0，63）、（63，63）以及它们在图像平面上的像素坐标，得到映射关系并计算吸盘圆心与标定板中心点在X、Y方向的偏移值lx=-0.765 9，ly=-2.113 6。 lz为标定板厚度，其值为6。根据式（17）可得

CTE=[-1.314 9 129.6215 75.973 6]Τ

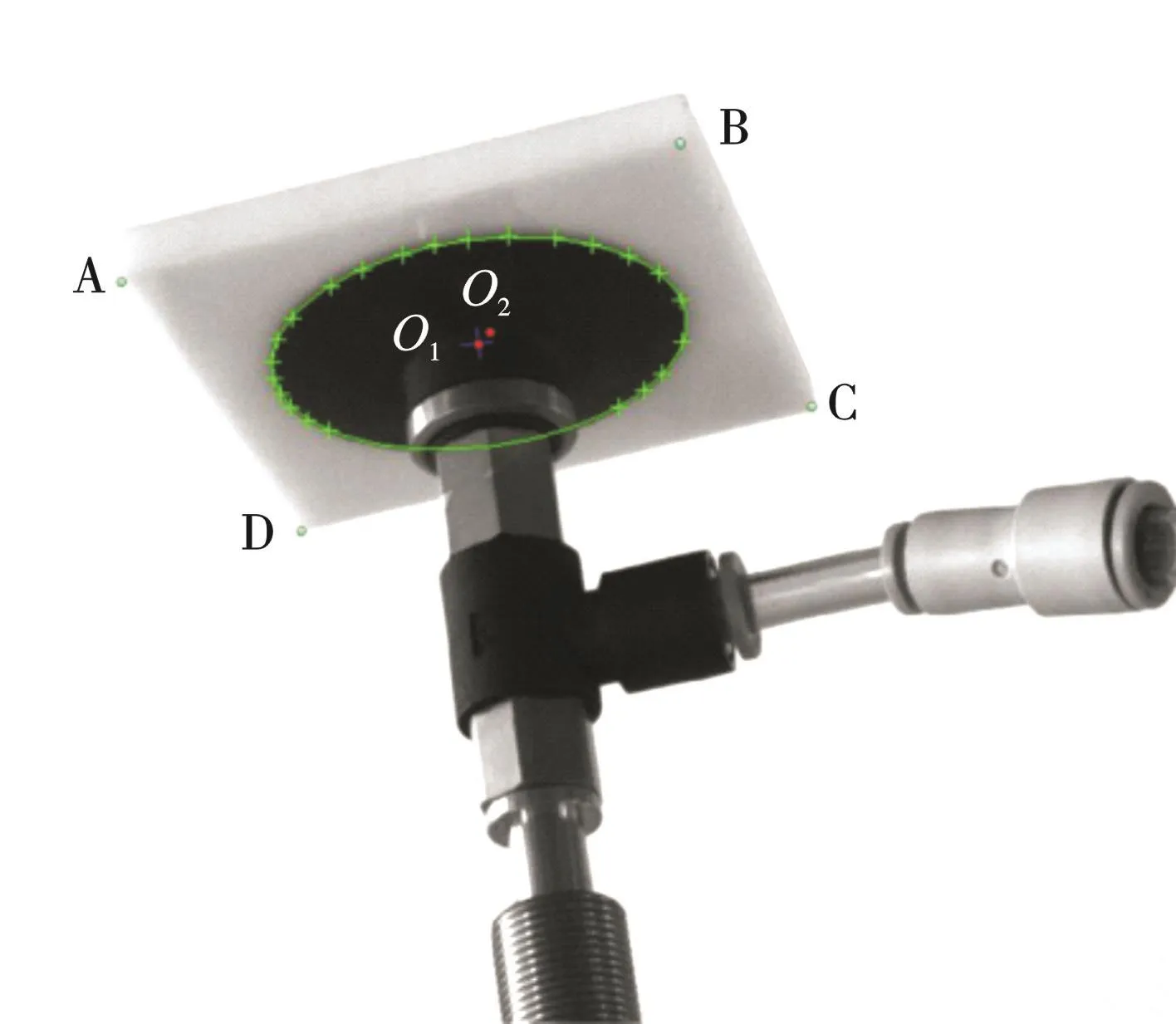
图5 标定板原点与吸盘中心的偏移量Fig.5 Offset between calibration board origin and sucker center coordinate

为验证结果的正确性，将本文方法与Halcon的手眼标定算法得到的标定结果进行对比。Hal⁃con的手眼标定算法流程为：①标定相机获得相机内参数；②改变机器人位姿，拍摄标定板图像，并通过机器人控制器记录此时机器人工具坐标系在基坐标系中的位姿，重复此过程10次；③对第②步中获取的标定板图像进行标定，得到每张标定板相对于相机坐标系的位姿关系，并根据标定板相对于相机坐标系的位姿关系以及相对应的工具坐标系在基坐标系中的位姿关系，用Halcon的calibrate_hand_eye算子计算得到最终的相机坐标系{C}相对于工具坐标系{E′}的位姿关系=[-1.716 77 129.999 9 75.590 7]Τ。相机坐标系原点与吸盘坐标系原点之间偏移值（x，y）的设计尺寸为（0，130）。Z方向偏移值为吸盘平面到相机坐标系原点的垂直距离，可以通过测量得到。在相机视野中放置标定板，移动吸盘至标定板所在面，记录Z方向的坐标值。将机器人沿标定板和吸盘平面的法线方向平移至最佳拍摄位置，记录机器人移动的距离参数，并获得标定板在相机坐标系下的位姿，将该位姿的Z方向的偏移量减去机器人移动的距离即为吸盘与相机在Z方向的偏移量，计算得出Z方向的偏移量为76.052 4。最后比较两结果并分别计算两结果与设计参数的平均误差，由计算可知：本文方法得到的结果与设计值的平均误差为0.590 7，而Halcon的手眼标定算法得到的结果与设计值的平均误差为0.726 2，本文提出的方法在精度方面要优于Hal⁃con手眼标定算法。

通过相机平移构建双目三维重建系统，如图6所示。图6b为相机在两个位置拍摄的物体图像，根据式（18）得到目标物体中心点相对于相机坐标系的位置［45.256 8 2.969 5 412.09］T。根据前面得到的手眼关系可以求出目标点相对于吸盘坐标系的位置［62.886 1-124.938 9-344.224 3］T。抓取结果如图6c所示，验证了该方法的正确性。基于镜面反射的手眼标定方法操作简便，不需要改变机器人的姿态，并且实验设备简单，只需要一块标定板和一个平面镜，就能完成实验。

图6 验证结果Fig.6 Verification result

4 结语

本文利用镜面位姿标定法标定相机和工具坐标系的位姿关系，通过相机平移构建双目视觉系统，实现对物体的三维重建，根据标定的结果，实现对物体的抓取。镜面位姿标定只需要3次改变平面镜的姿态即可完成，并且能够同时获得相机内参数以及相机坐标系和工具坐标系的位姿关系。标定过程中无需限制平面镜的姿态，可以确保选取最佳的拍摄位置而获得高质量的图片，有利于提高标定精度，且无需改变机器人的位姿，操作简单，易于实现。最后通过实验与Halcon标定算法进行对比，验证了所提方法的可行性。

［1］ 王敏，王万俊，黄心汉.空间物体定位的机器人手眼视觉标定方法［J］.华中科技大学学报（自然科学版），2001，29（3）：45-47.WANG Min，WANG Wanjun，HUANG Xinhan.Cali⁃bration Method of Robotic Hand-eye Vision for Object Orientation［J］.Journal of Huazhong University of Sci⁃ence and Technology（Natural Science），2001，29（3）：45-47.

［2］ XU Xiaohu，ZHU Dahu，ZHANG Haiyang，et al.TCP-based Calibration in Robot-assisted Belt Grinding of Aero-engine Blades Using Scanner Measurements［J］.The International Journal of Advanced Manufacturing Technology，2016，90（1/4）：1-13.

［3］ LI Jianfeng，ZHU Jianhua，GUO Yongkang，et al.Cali⁃bration of a Portable Laser 3-D Scanner Used by a Ro⁃bot and Its Use in Measurement［J］.Optical Engineer⁃ing，2008，47（1）：10.1117/1.2829766.

［4］ 杨广林，孔令富，王洁.一种新的机器人手眼关系标定方法［J］.机器人，2006，28（4）：400-405.YANG Guanglin，KONG Lingfu，WANG Jie.A New Calibration Approach to Hand-Eye Relation of Manipu⁃lator［J］.Robot，2006，28（4）：400-405.

［5］ 程玉立.面向工业应用的机器人手眼标定与物体定位［D］.杭州：浙江大学，2016.CHENG Yuli.Hand-Eye Calibration and Object Local⁃ization for Industrial Robotic Application［D］.Hang⁃zhou：Zhejiang University，2016.

［6］ 张召瑞，张旭，郑泽龙，等.融合旋转平移信息的机器人手眼标定方法［J］.仪器仪表学报，2015，36（11）：2443-2450.ZHANG Zhaorui，ZHANG Xu，ZHENG Zelong，et al.Hand-Eye Calibration Method Using Rotational and Translational Constraint Information［J］.Chinese Jour⁃nal of Scientific Instrument， 2015， 36 （11） ：2443-2450.

［7］ RUI R，JOÃO P B，URBANO N.Camera Pose Estima⁃tion Using Images of Planar Mirror Reflections［C］//Eu⁃ropean Conference on Computer Vision.Berlin，2010：382-395.

［8］ HESCH J A，MOURIKIS A I，ROUMELIOTIS S I.Mir⁃ror-based Extrinsic Camera Calibration［M］//Algorith⁃mic Foundation of RoboticsⅧ.Berlin：Springer，2009：285-299.

［9］ TSAI R Y，LENZ R K.A New Technique for Fully Au⁃tonomous and Efficient 3D Robotics Hand/Eye Calibra⁃tion［J］.IEEE Transactions on Robotics and Automa⁃tion，1989，5（3）：345-358.

［10］ ZHANG Zhengyou.A Flexible New Technique for Camera Calibration［J］.IEEE Transactions on Pat⁃tern Analysis and Machine Intelligence，2000，22（11）：1330-1334.

［11］ 林育斌.基于计算机视觉的三维重建技术研究［D］.天津：天津大学，2010.LIN Yubin.Research of 3D Reconstruction Based on Computer Vision［D］.Tianjin：Tianjin University，2010.

［12］ 杜歆，徐钢梅，朱云芳，等.一种基于单相机三维重建的简单方法［J］.传感技术学报，2007，20（8）：1917-1920.DU Xin，XU Gangmei，ZHU Yunfang，et al.A Simple 3D Reconstruction Method Based on Single Camera［J］.Chinese Journal of Sensors and Actuators，2007，20（8）：1917-1920.