高强度Helmholtz声源的声学特性研究
乔正辉 董 卫 程 梅 周树青
东南大学能源与环境学院,南京,210096
0 引言
近年来,声波控制细颗粒物的研究逐渐成为热点。在声波控制各类两相流中细颗粒物的迁移、悬浮、团聚或分离等行为时,常需要构造高强度声场,低能耗的稳定高声强声源成为该技术继续推进的关键[1-7]。
VAINSHTEIN等[1]利用四极对称声源形成的声场对不可压缩流体中细颗粒物进行迁移控制,强调声场强度越高,声波对流体中细颗粒物的控制越有效。NOORPOOR等[2]实验分析了平面驻波对烟道气体中粒径260~3 000 nm的细颗粒脱除的影响,认为高强度声场是分离气溶胶中颗粒的必要条件。ZHAO等[3]研究了驻波声场对团聚室内煤灰气溶胶颗粒的脱除,指出高声强有利于细颗粒的脱除,但由此引起的高能耗问题阻碍着声波技术的工业化进程。GLORIANA等[4]对号角状螺旋结构的声放大效果进行了研究,并设想利用外加号角构造高强度声场,但该技术没有显现出低能耗的优势。
旋笛可以产生高声强声波信号,但性能不稳且要求制作精细,难以在声波控制细颗粒物的应用中推广[5]。本课题组首次设计出一种高效的Helmholtz声源,使频率为1.286 kHz的声波信号强度放大13.3倍,为驻波烟气颗粒的分离提供稳定的强驻波声场[6-7]。
扬声器是将电信号转换为机械振动并向外辐射声功率的一种电声换能器[8],在声波控制细颗粒物的研究中,扬声器常作为构造声场的主要声源。Helmholtz共振器是一种特殊的声学元件,具有增强信号、扩声等功能[9-12],可有效改善换能器的性能[13]。目前,利用Helmholtz共振器提高扬声器声辐射功率的研究还比较少,文献[6-7]中的Helmholtz声源为解决高强度驻波声场中的能耗问题提供了一种思路,但尚未详细研究该声源的声学特性。
本文以文献[6-7]为基础,类比非线性光学腔,重点研究Helmholtz声源的声学特性。文中按照扬声器和Helmholtz共振器两者的尺寸关系,设计并制作了一款Helmholtz声源,根据结构特点对声源进行了动态类比,建立声源的等效声学模型。分析了Helmholtz声源的等效声阻抗的频率响应特性;同时,对比扬声器声源,对Helmholtz声源的两端电压、输出声压值和电声转换效率等随频率的响应特征进行了理论模拟和实验研究。通过对Helmholtz声源的声学特性研究,为解决声波技术应用中的能耗问题提供参考。
1 实验装置及测试系统
1.1 实验装置
Helmholtz声源由扬声器和圆柱形的Helm⁃holtz共振器组成;Helmholtz共振器由短管、空腔和扬声器的振膜组成。共振器材料为有机玻璃板材,板厚4.5mm。扬声器直径为40mm。Helmholtz声源的实物和结构见图1。

图1 实验装置Fig.1 Experimental device
Helmholtz共振器的共振频率与尺寸满足[6]

其中,共振频率 f0=1.823 kHz;共振器短管直径和长度分别为de=8 mm和le=4.5 mm;共振器空腔直径和长度分别为dt=35 mm和lt=4.5 mm;声速c0=342 m/s。
当扬声器向共振器空腔辐射的声信号频率与共振器的共振频率一致时,空腔内气体受到激发产生共振,增强入射的声信号,并经短管向外发射高强度声波。
1.2 测试系统
实验测试系统主要由信号发生器、传声器、电脑、NI数据采集系统、Helmholtz声源、扬声器和万用表组成,如图2所示。Helmholtz声源和扬声器声源分别采用接法1和接法2连接。信号发生器(SPF05)发出一定频率的周期性电信号,经声源转换为声信号后向外辐射。为降低传声器对Helmholtz声源短管出口声场的反射扰动,用传声器(B&KM PA416)采集距离声源d=2 cm处的声压值,传声器水平固定在声源中心轴线上。利用NIPXI-4472型数据采集系统对传声器获得的声信号进行处理,并基于LabVIEW软件,在电脑上对数据进行处理和记录。

图2 实验测试图Fig.2 Experimental test diagram
2 理论模型分析
Helmholtz声源中扬声器和Helmholtz共振器的尺寸足够小于入射信号波长。结合声学集中参量模型对Helmholtz声源进行模型分析,得到图3所示的声源类比电路,图中的参数定义见表1。

图3 Helmholtz声源类比电路Fig.3 Helmholtz sound source analogy circuit
根据导纳或阻抗类比[15],将图3中电路分别全部等效到电学端或声学端,声源的等效电阻抗Zin和等效声阻抗Zinn满足:
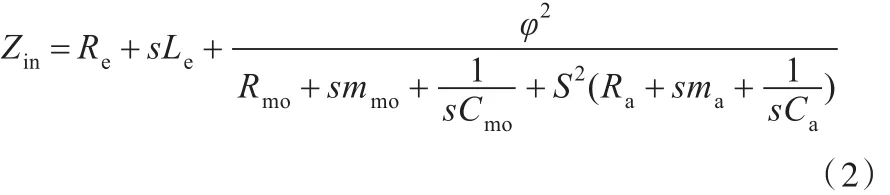

表1 等效类比电路参数Tab.1 Equivalent analogy circuit parameters
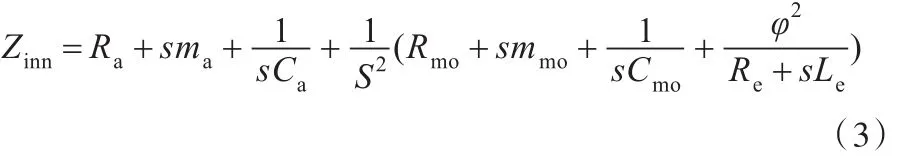
式中,ω为角频率,s=jω。
同理,扬声器的等效电阻抗Zλ[8]、等效力阻抗ZM[16]和等效声阻抗 ZM1为

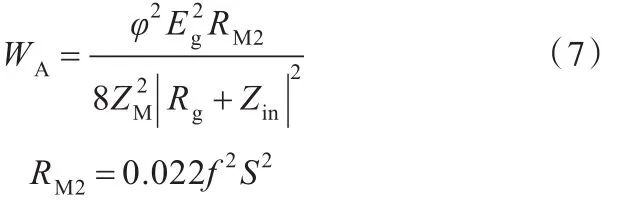
Helmholtz声源向外输出的声功率为式中,RM2为辐射阻;f为信号频率;Eg为信号电压峰峰值。
扬声器辐射的声功率Win与声压 pin的关系为[16]

式中,c0为介质声速;ρ0为介质密度;L为测压点与声源的距离。
Helmholtz共振器放大声压 pout与入射声压满足[17]:

式中,Za为Helmholtz共振器的等效声阻抗。
根据式(2)~式(10)和 L=lt,可得Helmholtz声源的输出声压值 pout和电声转换效率η表达式:
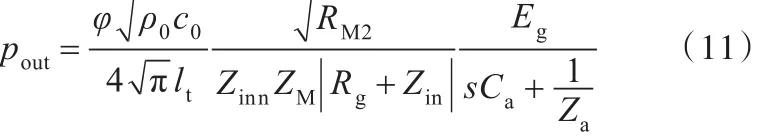

由式(11)和式(12)可以看出,Helmholtz声源的输出声压和电声转换效率同时与扬声器有关,并分别与Helmholtz共振器声压放大倍数的一次方和二次方成正比。
对比扬声器的电声转换效率[8]

由式(11)可知,共振器声压放大倍数是Helmholtz声源区别扬声器的主要因素。Helm⁃holtz共振器的共振声压放大倍数越大,越能提高Helmholtz声源的输出声压和电声转换效率。
3 实验测试与分析
3.1 Helmholtz声源声阻抗响应
Helmholtz共振器的声学参量Ra、ma和Ca的表达式如下[10]:

将式(1)中Helmholtz共振器的尺寸参数代入式(14)~式(16),计算共振器各声学参量,本文取ρ0=1.205 kg/m3。同时,参照文献[8]中扬声器物理参数的测量方法,采用实验测得扬声器的各物理参数,电阻 Re=6.5 Ω的扬声器各参数如下:Le=3.32×10-4H,Rmo=0.07 Ω,mmo=1.287×10-4kg,Cmo=4.18×10-3m/N,φ =0.412。
根据Helmholtz声源的理论模型,运用MAT⁃LAB软件编程对Helmholtz声源的阻抗频率响应特性进行数值模拟。由于声波除尘中最佳频率一般低于3 kHz[18],因此本文主要选取频率范围0~2.4 kHz进行分析。
对式(10)、式(6)和式(3)进行数值模拟,得到如图4所示不同结构的等效声阻抗随频率的响应特性。
图4a为Helmholtz共振器的等效声阻抗频响曲线,可以看出,在工作频率0~2.4 kHz范围内,等效声阻抗随着频率的增大先减小后增大,在1.82 kHz有唯一最小值,即可知Helmholtz共振器的共振频率为1.82 kHz,与式(1)中 f0=1.823 kHz近似相等。
图4b为扬声器的等效声阻抗频响曲线,可知等效声阻抗的变化趋势与Helmholtz共振器的相同,在0.21 kHz取得唯一极小值,极小值附近的声阻抗值变化比较尖锐。

图4 等效声阻抗的频率响应特性Fig.4 Frequency responses of equivalent acoustic impendence
图4 c为Helmholtz声源的等效声阻抗频响曲线,由图可知,Helmholtz声源的频响曲线与Helmholtz共振器相似,说明Helmholtz声源的等效声阻抗频率特性主要取决于共振器结构;区别在于,Helmholtz声源频响曲线的最小值为2.05 kHz,即声源的共振频率稍滞后于Helmholtz共振器的共振频率。这主要是由于扬声器取代了共振器的刚性背板,改变了Helmholtz声源的声阻抗随频率的变化特性。
3.2 Helmholtz声源电压响应
为分析Helmholtz声源的电压频率响应特征,将电阻 Re为 3.5 Ω、6.5 Ω和 7.3 Ω的 Helmholtz声源和扬声器分别按照图2所示接法1和接法2进行连接。向2种声源分别加载电压峰峰值为2 V、频率为0~2.4 kHz的正弦交流电信号。以0.1 kHz的幅度调节信号频率,利用万用表测量扬声器和Helmholtz声源两端的电压UV和电流值,并通过传声器1和2分别采集距离声源出口2 cm处的声压值。
根据万用表的测量数据,可得2种声源两端电压值随频率的变化曲线(图5)。

图5 2种声源的电压响应Fig.5 Voltage responses of 2 sound sources
图5 a为扬声器两端电压的频率响应特性,可以看出,在信号频率变化范围0~2.4 kHz内,电阻一定的扬声器两端电压随频率的增大先增大后减小,在频率为0.2或0.3 kHz处取得唯一的最大值,即扬声器的谐振频率近似为0.3 kHz。
图5b为Helmholtz声源两端电压的频响曲线,可以看出,电阻一定的Helmholtz声源两端电压随频率按照增大-减小-增大-减小的趋势变化,在信号频率为0.2 kHz或0.3 kHz以及1.8 kHz附近分别取得2个极大值,且频率分别对应扬声器的谐振频率和Helmholtz共振器的共振频率。
由图5可知,系统谐振时,电阻为3.5 Ω、6.5 Ω和7.3 Ω的Helmholtz声源的两端电压分别为0.701 V、0.715 V和0.720 V;扬声器的两端电压为0.705 V、0.717 V和0.723 V。对比两组声源的电压值可知,Helmholtz声源两端电压值较扬声器小。这主要是串联的共振器增加了声源的等效电阻,使Helmholtz声源在电学回路中的两端电压值减小。
3.3 Helmholtz声源声压响应
利用3.2节中传声器1和2采集的声压值,分别绘制实验中2种声源的输出声压值随频率的变化曲线,见图6a和图6b;同时,根据扬声器和Helmholtz共振器的参数对式(11)进行数值模拟,得到图6c的Helmholtz声源理论输出声压值频响曲线。

图6 2种声源输出声压Fig.6 Output sound pressures of 2 sound source
由图6a、图6b可知,两种声源的输出声压随频率的响应曲线都在2个频带内出现极大值,扬声器还在2.0 kHz附近出现反谐振频率。对比阻值为6.5 Ω的2种声源可知,Helmholtz声源在共振器共振时取得最大输出声压值,是扬声器的59.71/2.76≈22倍;在非共振区Helmholtz声源的输出声压值平均是扬声器的4倍,说明Helmholtz共振器具有增强声波辐射能力的功能。
由图6b、图6c可知,Helmholtz声源的输出声压值频率响应的实验结果和理论结果基本一致,验证了本文理论模型的适应性。在频率范围0~2.4 kHz内,Helmholtz声源的输出声压极大值分别位于 0.2~0.4 kHz和 1.5~2.4 kHz内。电阻为6.5 Ω的Helmholtz声源输出声压极大值分别为7.55 Pa和59.71 Pa。由 59.71/7.55≈8倍可知,在共振频带内,Helmholtz共振器具有较强的声压放大作用。
Helmholtz声源的输出声压值理论与实验结果稍有区别:一方面声源输出声压的实验值较理论值小;另一方面,实验中声源的共振频率较理论值超前。造成两者区别的原因,其一可能是理论模型误差或实验测试误差导致;其二可能是理论分析时使用的是给定的稳态声阻而在实验过程中声阻是非稳态的,从而导致共振频率的漂移。实验结果与理论结果近似一致。
3.4 Helmholtz声源的电声转换效率
Helmholtz声源在电声转换过程中,主要是利用Helmholtz共振器的共振效应增强声信号。利用Helmholtz共振器和扬声器的物理参数对式(12)和式(13)进行数值模拟;同时利用3.2节中扬声器和Helmholtz声源的电压、电流和输出声压实验值,计算2种声源的实际电声转换效率η和η′,并采用对数纵坐标(ln η 和 ln η′)绘制2种声源的电声转换效率频响曲线,见图7和图8。
由图7和图8可知,Helmholtz声源和扬声器的理论电声转换效率的频率响应与实验结果均保持一致。
图 7a中,电 阻 为 3.5 Ω、6.5 Ω和 7.3 Ω的Helmholtz声源在系统共振时 ln η峰值分别为-0.71、0.12和 0.04,可知 Helmholtz声源的电声转换效率η分别为48%、113%和104%;电阻为6.5 Ω的Helmholtz声源电声转换效率最大,展示出Helmholtz声源的声学非线性特征。图7中理论与实验结果稍有区别的原因,与图6b和图6c分析结论相似。
由图8a扬声器的电声转换效率频响曲线峰值,可计算电阻为 3.5 Ω、6.5 Ω和 7.3 Ω的扬声器实际最大电声转换效率分别为0.16%、0.21%和0.11%。

图7 Helmholtz声源电声转换效率Fig.7 Electric-acoustic conversion efficiency of Helmholtz sound source
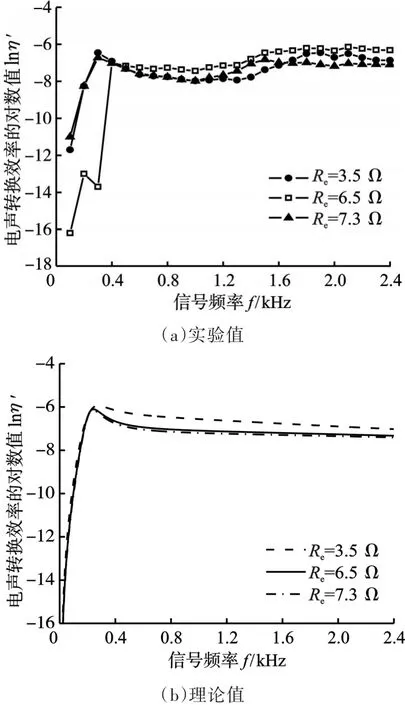
图8 扬声器电声转换效率Fig.8 Electric-acoustic conversion efficiency of speaker
对比图7和图8的实验结果可知,Helmholtz声源的实际电声转换效率远高于扬声器,电阻为6.5 Ω的Helmholtz声源共振时电声转换效率是扬声器最大电声转换效率的538倍(113%/0.21%≈538)。
4 结论
(1)Helmholtz声源的声学特性与扬声器和Helmholtz共振器的相互作用有关;Helmholtz声源的等效声阻抗特性主要由Helmholtz共振器决定。
(2)扬声器膜的谐振或Helmholtz共振器共振可以增强Helmholtz声源的声波辐射能力,但共振器的共振优于扬声器膜的谐振。在本文选定的实验工况下,电阻为6.5Ω的Helmholtz声源共振时的输出声压值约是扬声器的22倍,此时,Helmholtz声源的电声转换效率高达113%,是扬声器最大值的538倍。
[1] VAINSHTEIN P,SHAPIRO M.Aerodynamic Focusing in a Channel with Oscillating Walls[J].Journal of Aerosol Science,2008,39(11):929-939.
[2] NOORPOOR A R,SADIGHZADEH A,HABIBNEJAD H.Influence of Acoustic Waves on Deposition and Co⁃agulation of Fine Particles[J].International Journal of Environmental Research,2013,7(1):131-138.
[3] ZHAO Yun,ZENG Xinwu,TIAN Zhangfu.Acoustic Agglomeration of Fine Particles Based on a High Inten⁃sity Acoustical Resonator[C]//20th International Sym⁃posium on Nonlinear Acoustics(ISNA)Including the 2nd International Sonic Boom Forum(ISBF).Lyon,2015:060005.
[4] GLORIANA C,ERIN H G.Sound Amplification by Means of a Horn-like Roosting Structure in Spix's Disc-winged Bat[J].Proceedings of the Royal Society B-biological Sciences,2013,280:1-7.
[5] 刘新合.旋笛式调频声波清灰技术研究[J].机电工程技术,2012,41(12):43-44.LIU Xinhe.Experimental Study on Siren-style Fre⁃quency Modulation Sound Wave Cleaning Technology[J].Mechanical&Electrical Engineering Technology,2012,41(12):43-44.
[6] 乔正辉,黄亚继,董卫.对称Helmholtz声源圆柱形波导的声学谐振特性[J].东南大学学报(自然科学版),2014,44(3):579-584.QIAO Zhenghui,HUANG Yaji,DONG Wei.Acoustic Resonance Characteristics of Symmetric Cylindrical Waveguide with Helmholtz Sound Source[J].Journal of Southeast University:Natural Science Edition,2014,44(3):579-584.
[7] QIAO Z H,HUANG Y J,NASO V,et al.Aerosol Ma⁃nipulation by Acoustic Tunable Phase-control at Reso⁃nant Frequency[J].Powder Technology,2015,281:76-82.
[8] 马大猷.声学手册(修订版)[M].北京:科学出版社,1983:285-289.MA Dayou.Acoustic Manual(Revised Edition)[M].Beijing:Science Press,1983:285-289.
[9] DONG Mingrong,CHEN Kean,XU Xuezhong,et al.Theoretical and Experimental Study of a Prototype High-intensity Infrasonic Acoustic Generator[J].Jour⁃nal of Low Frequency Noise Vibration and Active Con⁃trol,2011,30(1):31-43.
[10] 马大猷.亥姆霍兹共鸣器[J].声学技术,2002,21(1/2):2-3.MA Dayou.HelmholtzResonator[J].Technical Acoustic,2002,21(1/2):2-3.
[11] TAKAHASHI H,SUZUKI A,IWASE E,et al.MEMS Microphone with a Micro Helmholtz Resonator[J].Journal of Micromechanics and Microengineering,2012,22:0850198.
[12] PILLAI M A,DEENADAYALAN E.A Review of Acoustic Energy Harvesting[J].International Journal of Precision Engineering and Manufacturing,2014,15(5):949-965.
[13] 桑永杰,蓝宇.多液腔Janus-Helmholtz水声换能器[J].哈尔滨工程大学学报,2013(10):1261-1266.SANG Yongjie,LAN Yu.Multicavity Janus-Helm⁃holtz Underwater Acoustic Transducer[J].Journal of HarbinEngineeringUniversity,2013(10):1261-1266.
[14] 翁泰来,韩捷.扬声器等效电路和应用[J].电声技术,2000(4):24-28.WENG Tailai,HAN Jie.Loudspeaker Equivalent Cir⁃cuit and Its Application[J].Audio Engineering,2000(4):24-28.
[15] 马大猷.现代声学理论基础[M].北京:科学出版社,2004:107-126.MA Dayou.TheoreticalFoundationsofModern Acoustics[M].Beijing:Science Press,2004:107-126.
[16] 杨洋,倪计民,褚志刚,等.基于波束形成的发动机噪声源识别及声功率计算[J].内燃机工程,2013,34(3):39-43.YANG Yang,NI Jimin,CHU Zhigang,et al.Noise Source Identification and Sound Power Calculation for an Engine Based on Beamforming[J].Chinese In⁃ternal Combustion Engine Engineering,2013,34(3):39-43.
[17] 姚丽,董卫,吴仲武.一种电磁式声电换能器的特性研究[J].电声技术,2013,37(1):33-38.YAO Li,DONG Wei,WU Zhongwu.Characteristic Research on Electromagnetic Acoustic-Electric Trans⁃ducer[J].Audio Engineering,2013,37(1):33-38.
[18] 张光学,刘建忠,周俊虎,等.频率对燃煤飞灰声波团聚影响的模型及实验验证[J].中国电机工程学报,2009,29(17):97-102.ZHANG Guangxue,LIU Jianzhong,ZHOU Junhu,et al.A Theoretical Model and Experimental Verifica⁃tion on the Influence of Frequency on Acoustic Ag⁃glomeration of Coal-fired Fly Ash[J].Proceedings of the CSEE,2009,29(17):97-102.

