基于奇异值分解的含权网络匿名化的安全性分析

曾勇，周灵杰，蒋忠元，刘志宏，马建峰

（西安电子科技大学网络与信息安全学院，陕西 西安 710071）

1 引言

目前，大数据已成为信息技术领域的研究热点。但是，大数据的发展依然面临许多问题，安全和隐私保护是目前人们公认的关键问题之一[1]。为了保护用户的隐私信息，数据拥有者一般会在发布数据之前对数据进行匿名化处理。数据发布匿名保护是实现数据隐私保护的核心技术和基本手段。数据的隐私保护要保证数据可用性和安全性之间的平衡。

社交网络的隐私保护不同于关系数据的隐私保护，它需要综合考虑网络的图结构、节点间的关系强度（权值）以及节点的重要性等信息。K-匿名[2]是关系数据隐私保护的经典方法之一，文献[3,4]将其推广到社交网络的数据隐私保护，分别提出了节点K-匿名和子图K-匿名，它们保证了对目标节点或子图再识别时，至少有K个候选者，从而使目标隐私泄露的概率小于。数据扰动[5～8]也是社交网络匿名化处理的一类常用方法，它主要对社交网络进行随机修改，使攻击者不能准确地推测出原始的真实数据，例如，文献[6]在图中加入高斯噪声，对网络中边的权值进行扰动，在指定节点之间最短路径及其序列保持不变的情况下，保证其最短路径长度的隐私性。但是这些方法都存在一定的不足，例如，文献[9]明确指出K-匿名方法存在信息损失问题，最重要的一点是它们往往对网络图结构破坏比较大，使扰动后图数据的可用性较低。

为了保护图数据的可用性，研究人员引入人工智能、图谱分析等理论，提出了基于降秩的方法，这些方法在图数据的谱空间可用性上远远优于上述方法。基于特征值分解方法[10]和基于奇异值分解（SVD,singular value decomposition）方法[11]是其中的2类经典方法，特征值与奇异值也称为图的谱。这2类方法通过舍弃范数小的谱及其对应的谱向量来保证图数据的隐私与谱空间主纬度上的数据可用性。文献[11]中给出了经典的奇异值分解扰动策略和稀疏化的奇异值分解扰动策略，并表明了此类方法能较好地保证图数据的可用性。Wu等[12]提出用特征值（奇异值）分解对扰动网络进行处理来提高数据的可用性。文献[13,14]将降秩方法引入网络的链路预测中，提出了一种基于低秩矩阵的全局信息预测算法。

基于降秩的方法虽能较好地保护图数据的可用性，但它并不总是安全的，仍然存在数据隐私泄露的风险。由于在基于降秩的方法中涉及舍弃谱，那么舍弃谱的数量是这类方法的关键。目前，在谱分析理论及其他相关理论中对舍弃谱的数量并没有公认的结论。虽然在原网络中舍弃谱越少，扰动网络的数据可用性越好，但在文献[10]对无权网络的特征值分解测试中发现，当舍弃谱的数量较少时，可以从扰动网络中恢复原网络。文献[15]采用文献[10]中所提的方法对城市电路网络的拓扑结构进行了测试，进一步表明了基于降秩的方法并不总是安全的，且其安全性与舍弃谱的数量有关。虽然文献[12]提出了用特征值（奇异值）相似性来决定所舍弃谱的数量，但这样只关注了数据的可用性而忽略了安全性，并且文中实验也表明了此方法会引入新的安全问题。文献[13,14]中给出了舍弃谱的数量的衡量方法，并且实验也表明该方法具有较好的链路预测效果，但其主要针对边缺失的预测问题及网络的动态变化问题所提出。此外，目前对基于降秩的社交网络隐私保护方法的安全性分析主要针对无权网络，而在含权网络中的安全性分析很少。

针对在含权社交网络中基于降秩的隐私保护方法的安全性问题，本文对其进行了分析与测试。目前，降秩的隐私保护方法主要基于奇异值分解和特征值分解，所以本文选择了具有代表性的基于奇异值分解的方法进行分析，并主要分析了奇异值分解扰动和稀疏化的奇异值分解扰动用于加权社交网络数据隐私保护时抵御重构攻击的能力。为了限定舍弃谱的数量，本文提出了-容忍性，它表示网络中冗余谱所占的比例。其中，ε为网络的可重构系数，表示在网络可被重构的情况下，可被舍弃谱的最大数量，为网络的可重构比例系数。当算法中舍弃谱的数量小于或等于ε时，网络可被重构，隐私数据将被泄露。本文指出目前的谱分析理论能给出的ε上界过于保守，并进行了大量实验来获取其数值解。实验发现这些网络对丢失的谱具有不同的容忍性，且ε、与网络参数之间存在一定的关系。同时测试了基于 SVD的双重扰动策略，用于加权社交网络隐私保护时的安全性。实验结果表明，基于 SVD的扰动策略对信息丢失具有一定的容忍性，直接用于社交网络的隐私保护存在被重构的风险，即使进行了双重扰动，也必须注意舍弃谱的数量。

2 基于奇异值分解的扰动策略

本节主要介绍了在加权社交网络中2种典型的基于奇异值分解的扰动策略。

2.1 奇异值分解扰动

文献[11]中作者将人工智能领域的奇异值分解用作数据扰动策略，来保护数据的隐私性。

一个含有N个节点、M条边的无向加权网络可以表示为G=(V,E)，其中，V代表节点的集合，E代表边的集合，顶点数N=|V|，边数M=|E|。若在边集E中存在元素eij，表示节点vi与节点vj之间存在的边。在加权网络G中每一条边eij都有一个权重wij=wji与之相对应。假设G无自环路且无多重边，则G可由其邻接矩阵A∈RN×N表示，其中

对于一个网络G的邻接矩阵A∈RN×N，必然存在一个完全奇异值分解

其中，U、V均为N×N阶的酉矩阵，Σ=diag[σ1,σ2,…,σN−1,σN]为对角矩阵，σi为A的奇异值。注：Σ 的对角元素非升序排列，即σ1≥σ2≥…≥σN−1≥σN≥0。

SVD扰动主要通过舍弃其部分较小的奇异值及对应的谱向量来实现对数据的扰动。令对角矩阵 Σj为舍弃j(j≥0)个较小的奇异值后的对角矩阵，则有

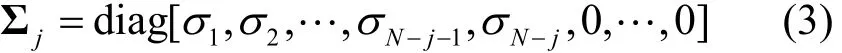
则SVD扰动后的邻接矩阵为

2.2 稀疏化的奇异值分解扰动

为了加强对数据的保护，文献[11]在SVD扰动的基础上对U、V矩阵做了进一步处理，并将这种对数据进行双重扰动的方法称为稀疏化奇异值扰动（SSVD，sparsified singular value decomposition）。SSVD的具体过程如下。

对邻接矩阵A进行奇异值扰动，得Aj。然后令

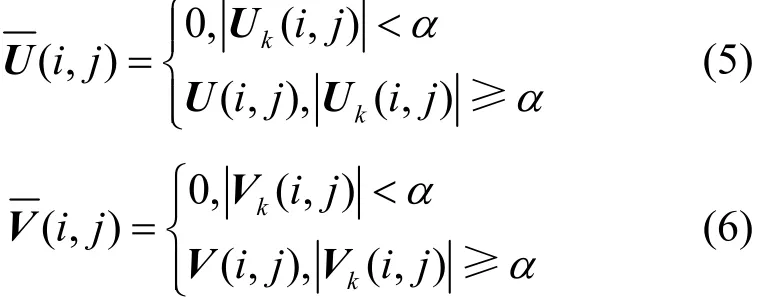
其中，α是U、V矩阵中数值的绝对值的下界。则扰动后的矩阵为

α是对矩阵中元素大小的限定，在不同类型的网络中，U、V矩阵的值分布差异可能较大，从而导致在α相同的条件下，在U、V矩阵中舍弃的值的比例无法评估。为了更好地适应不同类型的网络，使U、V中舍弃的值的数量更可控，本文定义β为U、V中删除的值的比例，即

其中，nα为U或V矩阵中舍弃值的个数。

3 重构方法及-容忍性

本节主要对无权网络特征值分解的重构方法[10]进行推广，提出在含正整数权重网络中的重构方法。对于含任意权重的社交网络，提出非精确重构的概念以及2种重构方法。为了分析降秩方法的安全性，提出了-容忍性，它反映了隐私数据何时会被泄露。同时，在3.4节对重构方法以及ε进行了理论上的分析。

3.1 重构的描述

在SVD扰动中，显然，j=0时Aj=A，j≠0时Aj≠A。当j≠0时，Aj中的值分布服从一定的规律。图1给出了在ER网络（N=100，p=0.5）中j=0、j=10、j=20以及j=30时Aj中值的分布情况（在其他模型网络中具有相同的结果），其中，A中的权值服从[1,5]之间的均匀分布。由图1可以看出，Aj中的值在[0,5]中各整数值的附近分布。

当j≠0时，Aj中的值含有非整数以及负值，本文试图用Aj重构A，以获得原网络的全部信息。令重构后的矩阵为，假设攻击者无任何背景知识，对于含有正整数权值的网络，定义为

假设攻击者已知网络权重的分布规律，为了能在j取值更大的情况下重构出网络，可以根据网络中值的分布情况对重构操作进行调整。例如，已知网络中的权值仅为偶数，为取得更佳的还原效果，则重构操作可以调整为

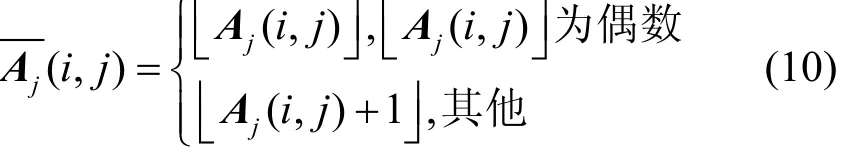
3.2 非精确重构

3.1节所提到的重构方法都是对含整数权重网络的精确重构，而对于含有任意数权重的网络来说，权值可能不全为整数，可能含有多位小数，这时若想精确地重构出原来的网络，代价是非常大的，有时甚至是计算不可行的。考虑到对某些值允许一定误差的存在，本节给出了非精确重构方法。

对于一个加权网络G，其邻接矩阵为A，若它的重构网络与它本身之间满足

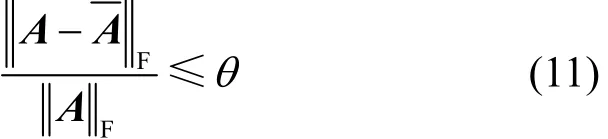
则称其中，||A||F表示矩阵A的F（Frobenius）范数[16]，定义为非精确重构出了A，记为

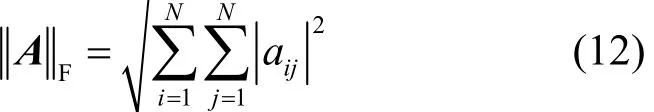
式(11)左边部分称为网络之间的值差[11]，为重构噪声矩阵，它们表示?相较A失真的程度。0≤θ≤1为用户阈值，用来限定非精确重构的程度。θ越小，重构出A，即与A就越相似，当θ=0时，

本文提出了2种非精确重构方法。假设原邻接矩阵A及其扰动邻接矩阵Aj，且A中权值最多含有nmax位小数，则这2种方法分别介绍如下。

方法 1 首先将原网络中权值整数化：Am=m×A，其中，m=10nmax（注：在小数位数较多的情况下，可以选择牺牲某些位，从而避免m太大引起的权值过大、处理困难等问题）。然后利用第 2节的方法对Am进行SVD扰动和重构。

方法 2 对重构方法进行调整以适应对权值为小数的匹配。重构方法调整为

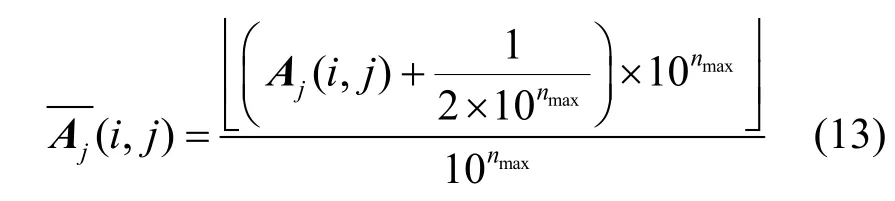
2种重构方法本质上是相同的，但由于2种方法在对原网络的处理上要求不同，就导致方法1必须准确地知道原网络的数据，而方法2根据原网络的特性来直接调整重构方法，所以只需要了解原网络的部分特性。方法1实质上是权重全部为整数时的非精确重构，所以对2种方法的测试可以说明含任意权值的网络的非精确可重构性。

3.3 -容忍性及可重构系数

当j在一定条件下对扰动网络进行重构时，可以重构出原邻接矩阵A，即为了衡量网络对信息丢失的容忍程度，本文定义了-容忍性。

定义1-容忍性。设网络G及其邻接矩阵A，其规模为N，A的扰动矩阵为Aj，重构矩阵为令ε为

称ε为G的可重构系数，称为G的可重构比例系数。

在删除网络中ε个谱及对应谱向量时，网络依然可以被重构，即-容忍性反映了网络中无用谱（或称冗余谱）所占的比例。一个网络中ε越大，基于降秩方法中需要舍弃的谱的数量就越大（保证网络不被重构的情况下），则在相同扰动条件下，网络被重构的概率越大。

3.4 ε取值的分析

对于邻接矩阵A的奇异值分解可以表示为

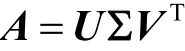
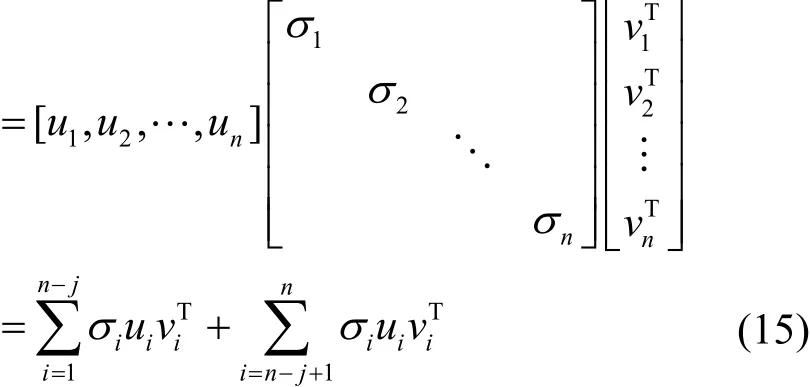
对于矩阵A中的任意一个元素aij可以表示为

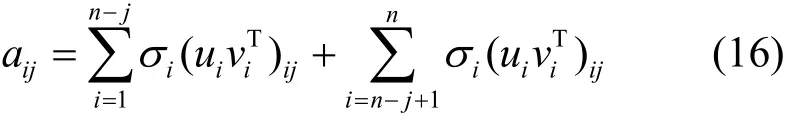
那么，当满足

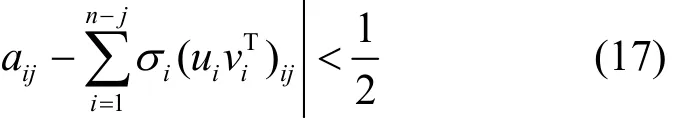
可以还原出原数据为

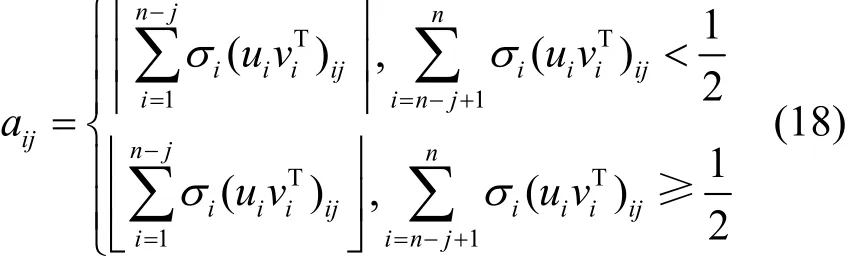
由此可见重构的条件为式(17)，即

考虑到社交网络的无向特性，则A为实对称矩阵。设λi为A的特征值，且|λ1|≥|λ2|≥…≥|λn|，由奇异值分解的性质[17,18]可得结论1。

结论 1σi=|λi|，vi=sign(λi)ui，若λi=0，则sign(λi)=1。

由此，式(19)左边的值可以表示为

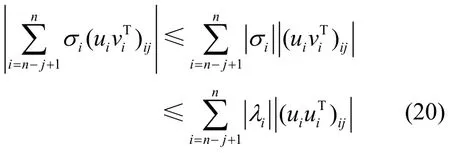
又因为U为酉矩阵[17]，那么它的n个行向量是两两正交的单位向量。由此可知||uiuiT||2≤1，继而可得|(uiuiT)ij|≤1，所以利用文献[10]求解可重构系数的方法，最终可得舍弃奇异值的数量的一个上界为

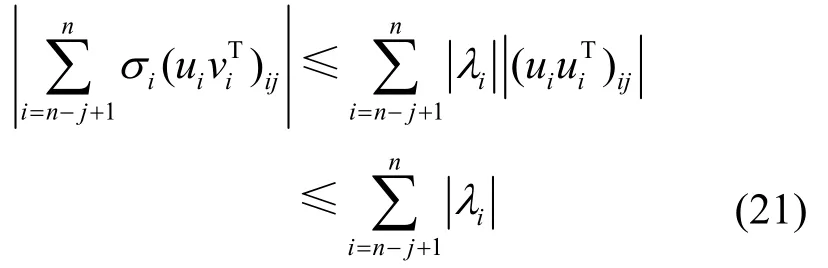
式(18)中的界是比较保守的，因为(uiuiT)ij可能存在负值。同时考虑到大多情况下网络将近一半的特征值为负值，由结论1可知，(uiuiT)ij为负值的可能性比较大，这就导致这个界是大于实际值的，而其下确界在矩阵谱分析理论中还没有公认的结论[19]，导致可重构系数的计算误差过大。换句话说，降秩方法中用此理论值作为舍弃的谱数量的依据可以保证网络不被重构，但此值不是最小值。接下来，本文通过实验来计算可重构系数的精确值。

4 网络的可重构系数

-容忍性反映了算法对网络中谱丢失的容忍程度，ε体现了算法中最少需要舍弃的谱的数量。ε、在一定程度上代表了网络的可重构性和一个网络经过SVD扰动后可被重构的概率。

由3.4节分析可知，ε理论计算误差较大，故本文通过实验来获取其数值解。4.1节主要测试了不同网络中的ε以及它与网络参数之间的关系。4.2节则针对本文提出的非精确重构方法，进行了测试与分析。同时，针对基于奇异值分解的双重扰动方法的安全性，4.3节测试了在SSVD扰动下网络的可重构性和非精确可重构性。为了便于分析，设本节测试的所有网络的权值均为服从[wmin,wmax]上的均匀分布，那么对含整数权重网络的重构采用式(9)所描述的方法。

本文所有的实验是在 Windows10专业版上的Matlab 2015B中进行的，电脑的配置为 Intel(R)Core™ i5-7500 CPU @3.40 GHz。

4.1 不同网络模型的可重构系数

4.1.1 ER网络

ER（Erdős-Rényi）网络[20]用随机图的方式来描述网络的拓扑结构，具有易于描述和分析的优点，是复杂网络研究的基本理论之一。本文生成的 ER无向加权网络采用G(N,p)模型，记为Gp(N,W)，其中，N为网络的规模。在此类网络中所有节点对之间以概率p相连接，且被随机赋予一个权重w。

首先，本文对ER网络中ε的分布情况进行了实验分析。实验所选取的网络规模为N=200，权值分布参数均为wmin=1、wmax=5，p分别取0.1、0.3、0.5、0.7以及0.9。本文对每种类型的网络取2 000个进行重构系数的计算然后求ε的平均值。图2显示了p取不同值时ε的分布情况，其中离散点是真实数据，曲线是用高斯分布拟合的结果，由此可以得到结论2。

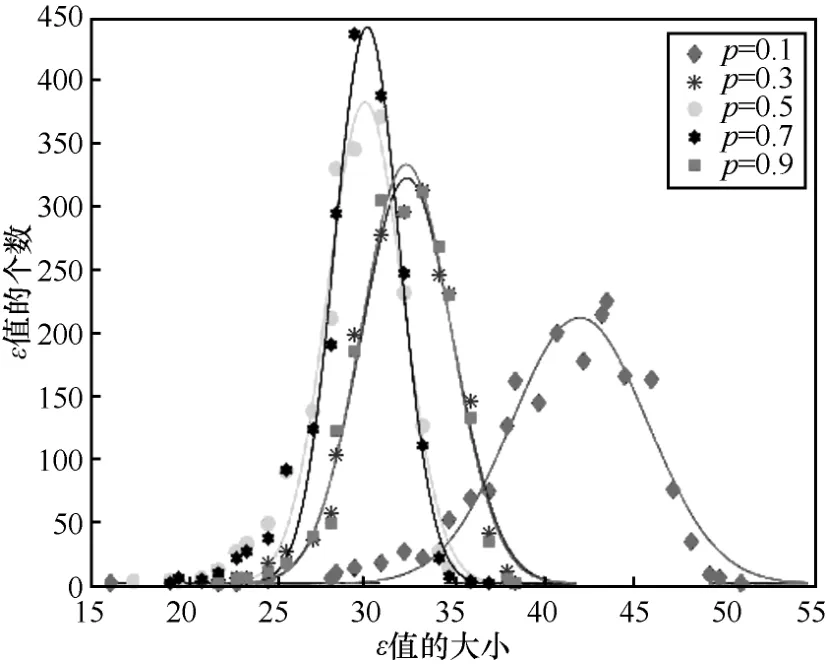
图2 ER网络中可重构系数的分布情况

结论2 ER网络中ε服从高斯分布。

由结论 2可知，对于相同类型的网络，其ε值存在差异，那么用其均值εm代表一种网络类型的重构系数是否合适，本文将对其进一步分析和测试。图3为G0.5(N,W)中ε均值与方差的关系，其中网络参数为wmin=1、wmax=5，N从50到1 000，每隔50测试1 000组数据计算均值与方差。从图3可以看出，ε的方差相较其均值εm很小，且在其他模型网络中也存在同样的规律，由此可以得到结论3。

结论 3 不能用单次实验结果代表网络的可重构系数，可以用多次实验的均值εm表示。

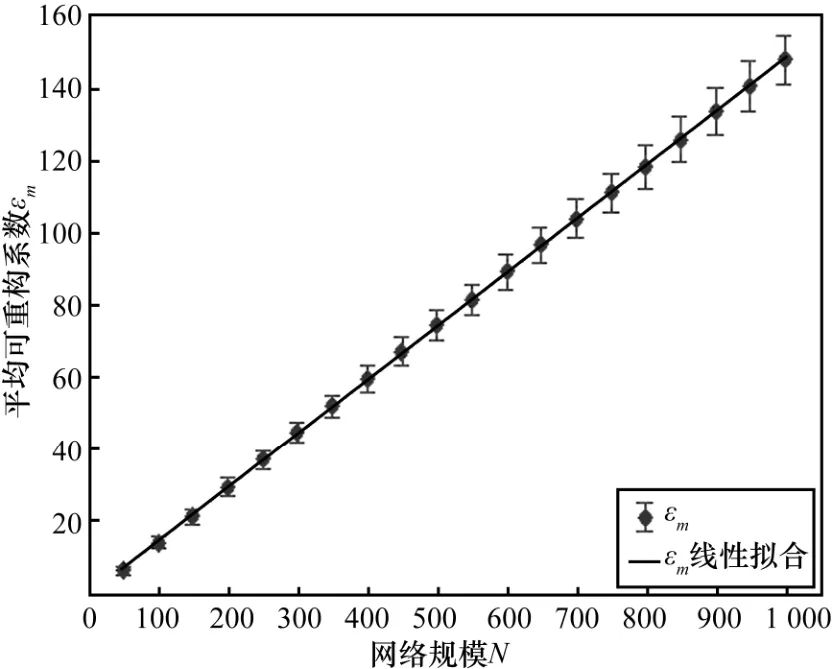
图3 可重构系数均值与方差的分布

接下来，本文测试了在ER网络中网络参数对εm的影响。首先，利用 2种类型的网络G0.2(N,W)与G0.5(N,W)对εm与N的关系进行了实验分析，其中权值服从[1,3]与[1,5]上的均匀分布。对于每种类型的网络，N取50到1 000，其中N每增加50取200个网络进行测试。图4显示了εm随N变化的情况，其中实线是拟合的结果。显然，εm与N呈线性关系，即-容忍性与网络规模无关。同时，网络的稀疏程度对有一定的影响，但相对较小。而网络中权值的分布却对其有较明显的影响。表1中展示了图4中的拟合结果：ε可高达 25%N，说明舍弃 25%的奇异值时，网络依然可能被重构。本文继续分析了权值分布参数（这里指wmax）对的影响。图5是在G0.5(200,W)中测试的结果，其中wmin=1，wmax取1到20，每隔1取1 000个网络进行测试。图5中离散点是真实数据，曲线是用幂律函数拟合的结果。由图5可知，wmax与之间存在幂律分布，且wmax越小，越大。

图4 ER网络中可重构系数与网络规模的关系

表1 ER网络的可重构比例系数

图5 ER网络中与权值分布的关系

图5中，当wmax为1时，网络可视为无权网络，此时，最大，为45%左右，这与文献[10]在无权网络中的结论基本保持一致，从而证明了本文所测数据的可用性。同时也表明了在无权网络中 SVD扰动方法的-容忍性大，被重构的风险大。

4.1.2 BA网络

BA（Barabasi-Albert）网络[21]是一种随机无标度网络，它的度分布服从幂律分布。本文用于分析的无标度网络采用 BA网络模型生成，记为G(m0,m)(N,W)，其中，m0代表初始节点的数量，m表示每增加一个节点所增加的边数。

本文首先利用 3种 BA网络：G(4,4)(N,W)、G(8,8)(N,W)、G(12,12)(N,W)，测试了εm与N的关系，其中，网络的权值分布参数为wmin=1、wmax=5，N从600到1 500，每隔100取200个网络进行测试。图6为测试结果，图6中的拟合结果如表2所示。由实验结果可知，εm与N之间存在线性关系，而网络参数m0、m对影响较小。

表2 BA网络的可重构比例系数

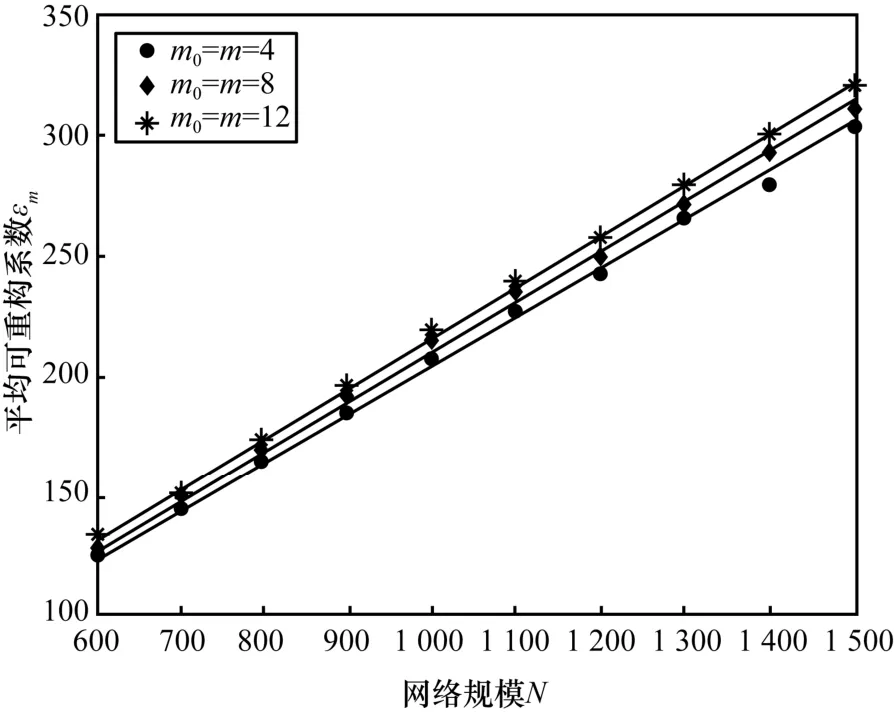
图6 BA网络中可重构系数与网络规模的关系

同时，利用这3种网络测试了权值分布对可重构系数的影响。图7给出了wmax与的关系，其中，N=600，wmin固定为1，wmax取1到20，每隔1取200个网络进行测试。由图7可知，wmax与之间同样存在幂律关系，且wmax越小，越大。当wmax=1，邻接矩阵A可视为无权网络，最大为50%，网络被重构的风险最大。

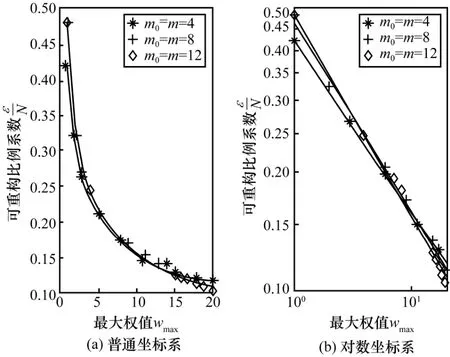
图7 BA网络中与权值分布的关系

4.1.3 小世界网络

小世界网络[22]是介于随机网络和规则网络之间的网络。WS（Watts and Strogatz）模型首先构造一个度为2×k的环形规则网络，然后再以概率p将边打乱重连。将 WS模型生成的网络记为G(k,p)(N,W)。

首先，对εm与N之间关系进行了测试。图8显示了当k为2、5，p为0.2、0.4、0.6时WS网络中εm与N的关系。其中，网络的权值分布参数均为wmin=1、wmax=5，N取50到500，每隔50取1 000个网络进行测试。表3给出了图8中的拟合值。实验发现，在不同的网络参数下，εm与N均存在线性关系，并且的取值取决于k和p的取值。

图8 WS网络中可重构系数与网络规模的关系

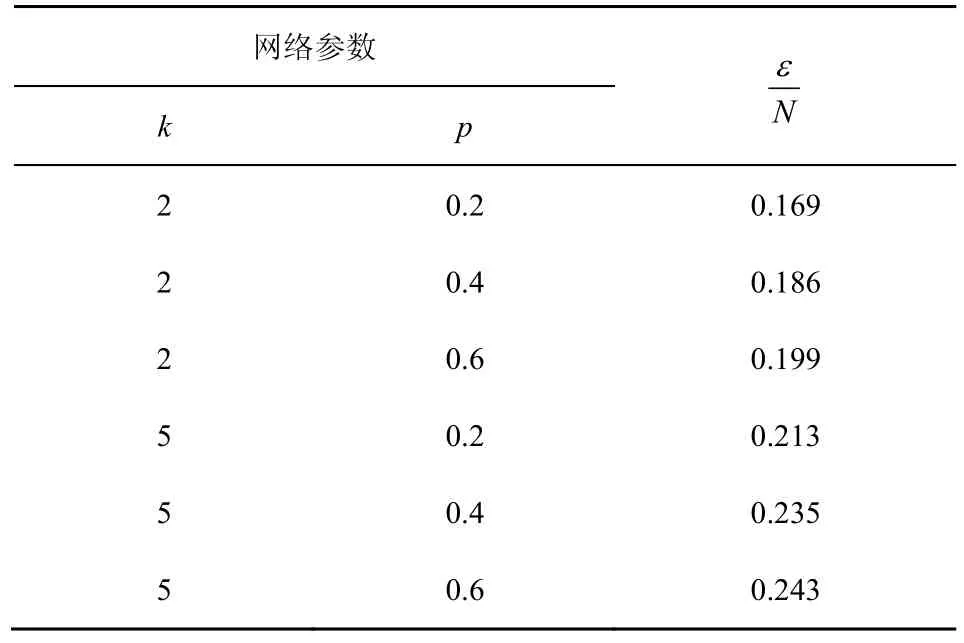
表3 WS网络的可重构比例系数

对于网络中权值分布参数wmax对εm的影响，本文在wmin=1，N=200，k=2、5，p=0.2、0.4时进行了测试分析，图9为实验结果。从图9可以看出，与wmax之间依然存在幂律关系，且wmax越小就越大。

4.1.4 实际网络

为了测试实际网络的-容忍性，本文对

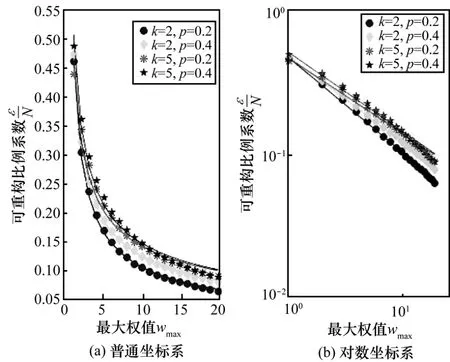
图9 WS网络中与权值分布的关系

4个真实数据集进行了实验，4个数据集分别为Facebook[23]、US Airlines[23]、Jazz[24]、Metabolic[23]。它们均为无向网络，包含的节点数分别为 4 039、332、198、453。为了测试权值不同时网络的容忍性，本文为网络中的每条边随机赋予一个服从均匀分布的正整数权值，并测试了wmin固定为1时wmax与εm的关系，图10为实验结果。从图10可以看出，实际网络对舍弃的维度信息具有不同程度的容忍度，在某些情况下舍弃45%的维度信息仍不能保证数据的安全性。

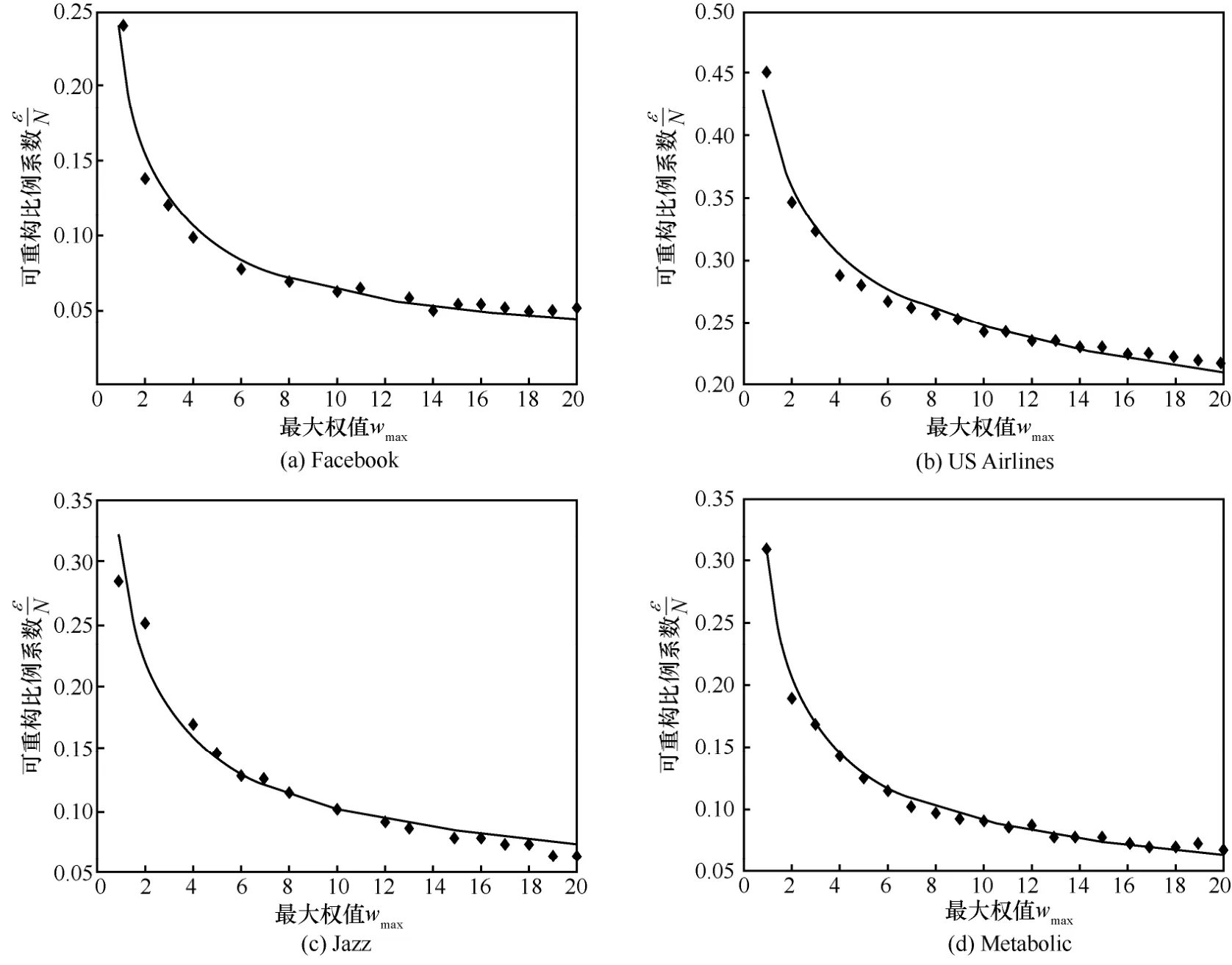
图10 实际网络中权值分布的关系

本节主要测试了不同网络的-容忍性。通过分析实验结果，可以得到以下结论。

结论4 BA、ER及WS网络中，可重构系数与网络规模存在线性关系，可重构比例系数与网络规模无关，即-容忍性与网络规模无关。

结论5 BA、ER及 WS网络中，当网络中权值为整数且服从[1,wmax]上的均匀分布时，wmax与之间存在幂律分布，且wmax越小，越大。

通过对各种网络-容忍性的测试发现，SVD扰动对网络维度的舍弃具有一定的容忍性，甚至在BA网络中可高达50%，由此可得结论6。

结论6 SVD扰动方法用于含整数权重的社交网络的数据隐私保护并不总是安全的，存在被重构的危险。

4.2 非精确重构中的可重构系数

为测试含任意权重网络的-容忍性，本文利用ER网络对2种非精确重构方法中的可重构系数进行了测试。首先测试了εm与网络规模N的关系，图11为实验结果。

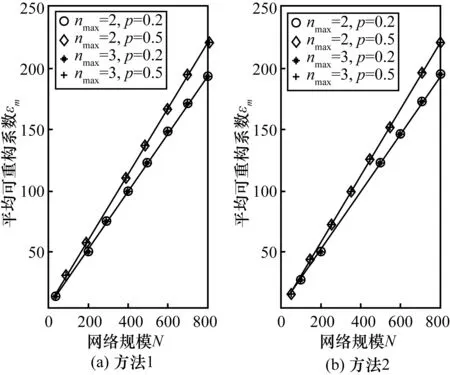
图11 非精确重构中可重构系数与网络规模的关系

由图11可以看出，εm与N同样存在线性关系，同时也可以看出nmax对重构系数基本没有影响。表4给出了可重构比例系数a的拟合值，对比方法1与方法2可以发现，它们的结果是保持一致的。

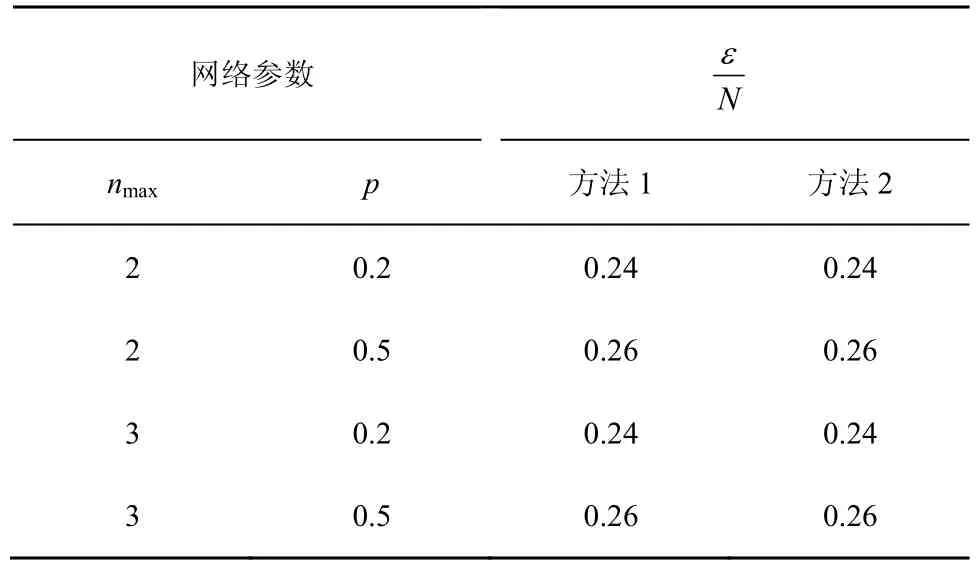
表4 非精确可重构比例系数

图12为利用ER网络Gp(200,W)测试与wmax关系的结果，可以发现在非精确重构中权值的分布对重构系数不再有明显的影响。这是由于非精确重构的定义相对于原网络的值而言并不是绝对的，在ε取值相同的条件下，网络中权值越大，重构噪声矩阵中的值就越大。最后利用 ER网络Gp(200,W)测试了θ与重构比例系数的关系。

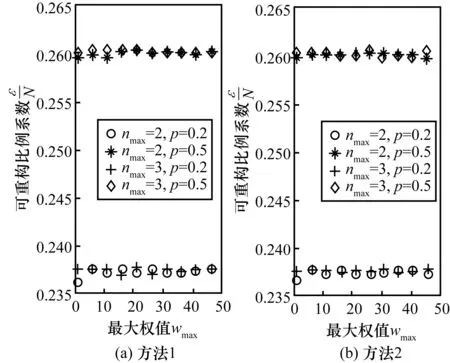
图12 2种非精确重构方法下可重构比例系数与权值分布的关系

图13是2种非精确重构方法下可重构比例系数与θ的关系，其中曲线是用幂律分布拟合的结果。由此可看出θ与服从幂律分布。

由4.1节的实验可知，在各模型网络及实际网络中，ε与N以及与wmax之间具有相同的规律。本节选取ER网络为代表，由实验结果可得以下结论。

结论7 在非精确重构中，BA、ER及WS网络中可重构系数与网络规模之间存在线性关系；可重构比例系数不受网络权值分布的影响；非精确重构阈值与可重构比例之间存在幂律关系，且阈值越大，可重构比例越大。

结论8 SVD扰动用于任意权值的社交网络隐私保护时，存在被非精确重构的危险。

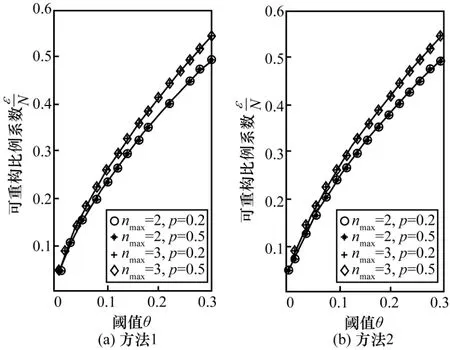
图13 2种非精确重构方法下可重构比例系数与θ的关系

4.3 双重扰动时网络的可重构系数

对邻接矩阵A进行稀疏化奇异值扰动后，在j≤ε的条件下依然可以利用上面提到的方法重构或非精确重构A，并且εm与N依然存在线性关系。由4.1节可知，在各模型网络中ε与N之间存在相同的关系，所以本文利用具有代表性的ER网络G0.5(N,W)测试了在不同β值下εm与N的关系，其中，N取50到800，每隔50取100个网络进行测试。图14是在权重全部为整数的情况下对A重构的结果，其中网络的权值服从[1,5]上的均匀分布。图15是在权重为任意值时对A非精确重构的结果，其中，nmax=2，且网络的权值均服从(0,5)上的均匀分布，非精确重构阈值θ=0.1。从图14和图15可以看出，当β高达16%时，Aj将不再能重构邻接矩阵A；当β高达30%时，将不再能非精确重构邻接矩阵A。而当β=4%左右时，Aj重构邻接矩阵A基本不受影响；当β=6%左右时，非精确重构邻接矩阵A基本不受影响，由此可得结论9。

结论 9 SSVD用于加权社交网络数据的隐私保护时，存在被重构和被非精确重构的危险。

本节主要在 SVD扰动下测试了不同含权网络的可重构系数，发现了可重构系数、可重构比例系数与网络参数之间存在的关系。针对含任意权重网络的可重构系数，在 ER网络中采用非精确重构方法进行测试，发现了可重构系数、可重构比例系数与网络参数之间存在的关系。最后，对基于奇异值分解的双重扰动策略，分别采用重构和非精确重构测试了其可重构系数。实验结果表明，即使进行了双重扰动，网络依然会表现出不同程度的-容忍性，从而说明了基于奇异值分解的扰动策略用于加权社交网络的隐私保护时具有被重构的危险。

图14 SSVD中β对网络重构的影响

图15 SSVD中β对非精确重构的影响

5 结束语

本文测试并分析 SVD扰动方法用于加权社交网络的安全性，提出了网络的-容忍性，ε越大，网络被重构的概率越大，越不安全，并分别用理论和实验对网络的-容忍性进行了分析，同时实验测试了网络非精确重构时的-容忍性和在 SSVD扰动下的-容忍性。实验发现，BA、ER及 WS网络中，-容忍性与网络规模无关，同时表明了SVD扰动对含权社交网络信息的丢失具有较大的容忍性，即使在双重扰动中舍弃少于5%～50%的维度，依然存在被重构和被非精确重构的危险。

本文的分析与测试建立在权值服从均匀分布的基础之上，下一步的工作将考虑非均匀分布权值下可重构系数、可重构比例系数与网络结构之间的关系。同时，在重构方法中考虑攻击者背景知识的影响也值得进一步研究。

[1] 冯登国, 张敏, 李昊. 大数据安全与隐私保护[J]. 计算机学报,2014, 37(1)∶ 246-258.FENG D G, ZHANG M, LI H, et al. Big data security and privacy protection[J]. Chinese Journal of Computers, 2014, 37(1)∶ 246-258.

[2] WONG R C W, LI J, FU A W C, et al. (α,k)-anonymity∶ an enhancedk-anonymity model for privacy preserving data publishing[C]//The 12th ACM SIGKDD international conference on Knowledge discovery and data mining. 2006∶ 754-759.

[3] CORMODE G, SRIVASTAVA D, YU T, et al. Anonymizing bipartite graph data using safe groupings[J]. The VLDB Journal—The International Journal on Very Large Data Bases, 2010, 19(1)∶ 115-139.

[4] CHENG J, FU A W, LIU J.K-isomorphism∶ privacy preserving network publication against structural attacks[C]//The 2010 ACM SIGMOD International Conference on Management of Data. 2010∶ 459-470.

[5] ABAWAJY J H, NINGGAL M I H, HERAWAN T. Privacy preserving social network data publication[J]. IEEE Communications Surveys &Tutorials, 2016, 18(3)∶ 1974-1997.

[6] LIU L, WANG J, LIU J, et al. Privacy preserving in social networks against sensitive edge disclosure[R]. Technical Report Technical Report CMIDA-HiPSCCS 006-08, 2008.

[7] DAS S, EĞECIOĞLU Ö, EL ABBADI A. Anonymizing weighted social network graphs[C]//2010 IEEE 26th International Conference on Data Engineering (ICDE). 2010∶ 904-907.

[8] LI Y, LI Y, YAN Q, et al. Privacy leakage analysis in online social networks[J]. Computers & Security, 2015, 49∶ 239-254.

[9] 苏洁, 刘帅, 罗智勇, 等. 基于信息损失量估计的匿名图构造方法[J].通信学报, 2016, 37(6)∶ 56-64.SU J, LIU S, LUO Z Y, et al. Method of constructing an anonymous graph based on information loss estimation[J]. Journal on Communications, 2016, 37(6)∶ 56-64.

[10] LIU D, WANG H, VAN M P. Spectral perturbation and reconstructability of complex networks[J]. Physical Review E, 2010, 81(1)∶ 016101.

[11] XU S, ZHANG J, HAN D, et al. Singular value decomposition based data distortion strategy for privacy preserving[J]. Knowledge and Information Systems, 2006, 10(3)∶ 383-397.

[12] WU L, YING X, WU X. Reconstruction from randomized graph via low rank approximation[C]//The 2010 SIAM International Conference on Data Mining, Society for Industrial and Applied Mathematics. 2010∶ 60-71.

[13] PECH R, HAO D, PAN L, et al. Link prediction via matrix completion[J]. EPL (Europhysics Letters), 2017, 117(3)∶ 38002.

[14] XU X, LIU B, WU J, et al. Link prediction in complex networks via matrix perturbation and decomposition[J]. Scientific Reports, 2017, 7(1)∶ 14724.

[15] SARKAR S. Spectral (re) construction of urban street networks∶ generative design using global information from structure[M]//Design Computing and Cognition'14. Springer International Publishing, 2015∶ 41-55.

[16] 张贤达. 矩阵分析与应用(第2版)[M]. 北京∶ 清华大学出版社, 2013.ZHANG X D. Matrix analysis and applications.(second edi-tion)[M].Beijing∶ Tsinghua University Press, 2013.

[17] 戴华. 矩阵论[M]. 北京∶ 科学出版社, 2001.DAI H. Matrix theo-ry[M]. Beijing∶ Science Press, 2001.

[18] HORN R A, JOHNSON C R. 矩阵分析[M]. 天津∶ 天津大学出版社, 1989.HORN R A, JOHNSON, C R, Matrix analysis[M]. Tianjin∶ Tianjin University Press, 2001.

[19] ZHANG X D. Matrix analysis and applications[M]. Cambridge University Press, 2017.

[20] ERDŐS P, RÉNYI A. On the evolution of random graphs[J]. Transactions of the American Mathematical Society, 1984, 286(1)∶ 257-274.

[21] BARABÁSI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439)∶ 509-512.

[22] WATTS D J, STROGATZ S H. Collective dynamics of “small-world”networks[J]. Nature, 1998, 393(6684)∶ 440-442.

[23] ABUELHAIJA S, PEROZZI B, ALRFOU R. Learning edge representations via low-rank asymmetric projections[C]//The 2017 ACM Conference on Information and Knowledge Management. 2017∶ 1787-1796.

[24] GLEISER P M, DANON L. Community structure in jazz[J]. Advances in Complex Systems, 2003, 6(4)∶ 565-573.