支持高效密文密钥同步演化的安全数据共享方案

严新成，陈越，贾洪勇，陈彦如，张馨月

（1. 解放军信息工程大学数据与目标工程学院，河南 郑州 450001；

2. 郑州大学软件与应用科技学院，河南 郑州 450001； 3. 公安部第一研究所，北京 100048）

1 引言

随着云计算技术的推广应用，数据加密已成为保护用户云端数据隐私的常用方法。与此同时，数据共享的灵活性、高效性与安全性也成为该领域的研究热点。

一方面，基于分布开放的计算环境中日益增加的数据共享和处理需求，资源提供方需要制订灵活可扩展的访问控制策略来控制数据的共享范围并保证关键数据的机密性，大规模分布式应用也迫切需要支持一对多的通信模式[1]。而传统的访问控制模型在应对新型存储模式下数据共享的需求时，往往存在灵活性不足、安全机制缺乏等问题。基于此，许多新型密码算法被应用到云存储系统中，可以支持数据细粒度访问及私钥撤销，加解密效率也接近实用，在学术界和产业界均取得了很大成果[2,3]。其中，基于身份的加密[4]以及基于属性的加密方案[5]能够保证数据的安全性，但前者资源提供方需要使用接收群体中每个用户的公钥加密消息并将密文分别发送给相应的用户，导致计算开销大、占用带宽多；后者虽然支持资源提供方自定义访问控制策略，增强了数据的自主访问控制能力，但涉及用户或属性撤销时，客户端计算开销过大。而广播加密方案中资源提供方对于数据的访问约束简单高效，通过维持解密用户集合即可满足外包环境下安全灵活的数据共享需求。

另一方面，由于当前计算机系统架构固有的静态特点，在利用软硬件构造加密云存储系统时不可避免地引入许多安全漏洞。现实中的云数据泄露事件大部分缘于这种软硬件漏洞利用攻击，使许多高强度的加密机制形同虚设[6]。例如，当加密系统内部存在较大固定性因素时，攻击者就可以根据已经发现的如认证机制漏洞、软硬件漏洞、加密算法实现漏洞等对其发起攻击，以巧妙的方式绕过最坚固的防线，获取密文密钥并解密用户存储在云端的数据[7,8]。

加密云存储系统易受到攻击的根源还来自于加密方案实施过程和密文存储的确定性，即密文生成后在其整个生命周期中均处于静止状态，不发生任何变化，直到失去用处被删除，且密文更新依赖于数据重加密。这容易造成以下问题：1) 撤销权限的用户仍然能够利用持有的私钥解密之前的密文，即密文不具备前向安全性；2) 密文密钥的长期不变性使攻击者在搜集到对应的密文密钥后即可解密，而与版本或时间周期无关。此外，加密云存储系统私钥分发流程的确定性使攻击者可以从多个环节发起攻击，如根据用户在认证过程中暴露的身份、位置等信息刺探合法用户的隐私，或仿冒用户身份直接从授权中心获取私钥。

因此，当利用加密技术来构建安全云存储系统时，在密码学方案中减少确定性和引入随机性十分必要。考虑到安全灵活的数据访问需求以及密文存储的静态性特点，本文从广播加密方案入手，研究支持高效密文密钥同步演化的云数据安全共享方案，即在加密云存储系统中实现安全数据共享的同时保证密文密钥周期性同步演化，一方面可避免重加密带来的巨大开销，另一方面可增加密文存储的动态性，增大攻击者的攻击难度。

2 相关工作

作为美国近年来提出的网络空间“改变游戏规则”的革命性技术之一，移动目标防御[9]为解决“易攻难守”这一当前网络安全面临的重要问题提供了新的思路[10]。其核心思想是通过自动改变一个或多个系统属性使系统攻击表面对攻击者而言不可预测，从而增加攻击者的攻击难度，提高系统的弹性和安全性[11]。文献[12]提出保护已认证客户抵御分布式拒绝服务（DDoS, distributed denial of service）攻击的移动目标防御机制，文献[13]针对现有路径跳变技术路径选取的盲目性、跳变实施缺乏约束性等问题，提出基于最优路径跳变的网络移动目标防御技术。

主动防御技术作为网络空间防御技术的新星，研究热度不断提高。就国内主动安全防御研究而言，邬江兴院士最早提出拟态安全防御技术，其基本思路是以不确定性对抗未知威胁。文献[14]以入侵容忍技术和移动目标防御技术为主线概括了主动防御技术的发展，并介绍了拟态防御技术理论、工程实践以及测试情况。文献[15]在对已有防御技术的问题和不足进行深入分析的基础上提出基于“动态异构冗余”结构的拟态防御模型。

文献[16～20]均可实现基于属性加密的云存储数据共享方案，但属性撤销及密文更新过程计算开销大，且未能考虑将时间、环境等因素引入加密方案中来增加密文存储的动态性与随机性。广播加密[21]提出时间较早，但作为一种将数据内容通过广播信道安全地分发给合法用户的安全机制，近年来相关研究仍层出不穷。文献[22]给出固定密文密钥大小的自适应选择密文攻击（CCA, chosen ciphertext attack）安全的广播加密方案。文献[23]提出一种广播加密和属性加密相结合的高效隐私保护方案。文献[24]研究了支持高效加密过程和较短密文长度的广播加密方案。当进行密文演化时，上述方案均需进行密文重加密，计算开销过大，不适用于用户频繁变动的场景。

和移动目标防御技术类似，拟态安全防御理论主要从硬件指令与软件系统等层面出发研究如何通过主动变换提高系统抗攻击能力。而本文提出的CKSE-SDS方案实际上是把拟态变换思想应用到云存储加密系统的密文演化中，通过增加存储密文的动态性和随机性来提高系统的安全防护能力。其基本思路是在广播加密方案中通过引入密码学累加器构造密文密钥动态分割与融合所必需的变换因子，由此实现高效的密文密钥同步演化，进而增加加密过程的随机性，降低攻击者利用系统固有的安全漏洞获取密文密钥来破解密文的概率。此外，在用户私钥撤销及密文演化过程中，只需对用户私钥及密文的部分构件进行更新，能够有效提升加密方案的运行效率。

3 预备知识

3.1 双线性映射

G和G1是2个阶为素数p的群，g是G的生成元，e∶G×G→G1是一个双线性对，G和G1是上述2个群，那么双线性对具备以下性质。

1) 双线性：即对于所有的群元素u,v∈G，可以得到e(ua,vb) =e(u,v)ab。

2) 非退化性：e(g,g)≠ 1。

3) 可计算性：对于任意的g,h∈G，存在多项式时间算法来计算e(g,h)的值。

3.2 Diffie-Hellman Exponent假设

CKSE-SDS方案安全性依赖于 Diffie-Hellman Exponent假设，Boneh等[25]证明该假设在一般群模型中是困难的。G中l-BDHE问题定义如下。

(h,g,gα,g(α2),…,g(αl),g(αl+2),…,g(α2l))∈G2l+1是给定的长度为2l+1的向量，要求能够计算出。这里，假设，如果有那么攻击者将能够以ε的概率攻破l-BDHE困难问题。l-BDHE的判定困难问题可以采用类似的定义，即如果式(1)成立，那么算法B将能够以ε的概率解决判定l-BDHE困难问题。

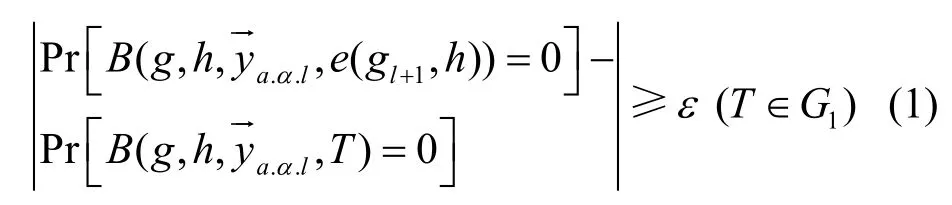
如果不存在多项式时间算法以ε的概率攻破判定l-BDHE困难问题，那么判定(t,ε, l)-BDHE 困难问题成立。如果设定其中，当收到输入时，如果算法能够输出gl+1，表明攻击者攻破了l-BDHE困难问题。

3.3 RSA累加器

密码学累加器能够把一个集合中的所有元素压缩成一个很短的数值，同时为集合中每个元素生成一个隶属于该集合的证明值。任何参与实体只要获得了一些公开信息，即可验证所持有元素是否属于累加值所代表的集合。具体过程如下。

1) 压缩方法

假设有一个集合η，该集合有n个kbit的元素{e1,e2,… ,en}，N是一个ybit的RSA模，即N=pq，其中，p和q均是强素数。可以把集合η压缩成一个ybit的整数，方法为

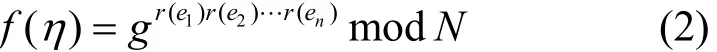
其中，g∈QRN,r(ei)是一个3kbit的素数代表值，RSA累加器的公钥是由RSA模N、幂基g和2个通用的散列函数构成。素数的代表值是对原始元素的一种变换，主要是为了提高方案的安全性和正确性。

2) 生成成员隶属关系证明值

一旦计算出整个集合的累加值，那么每个元素相对于该集合的成员关系证明值也可以计算出来，对于原始集合η中的元素ei，其证明值计算为

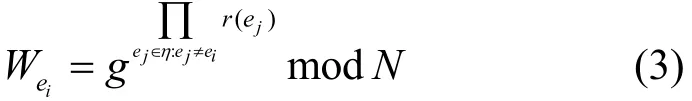
3) 成员隶属关系验证

一旦获得集合η中的所有元素的累加值f(η)以及每个元素的证明值Wei，就可以验证该元素是否隶属于这个集合，计算方法如下。

检查等式是否成立。如果成立，该元素隶属于集合；否则，该元素不属于集合η。

4 CKSE-SDS方案设计

4.1 构造思想

本文方案采用密码学累加器技术构造拟态变换因子，包括密钥拟态变换因子和密文拟态变换因子2类。密码学累加器和散列函数类似，散列函数作为一种压缩映射方法，能够将任意长度的消息压缩为某一固定长度的消息摘要，而密码学累加器可以把累加器集合中的多个元素压缩成一个具有特定比特长的整数（见3.3节）。当集合中任意一个元素发生改变时，累加值相应变化。此外，集合中每一个元素均有一个证明值，用于该元素与集合从属关系的验证。

利用密码学累加器的这一特点，可以进行拟态变换因子的构造。该方案中，用户解密私钥包括2个部分，一部分相对固定，在系统初始化阶段生成，另一部分跟随时间周期变化。在每个时间周期的开始，密钥授权中心把当前时刻t加入累加器中，并且为累加器集合中的每个元素计算生成相应的证明值。授权中心把周期性更新的累加器值（密文拟态变换因子）和每个成员对应的证明值（密钥拟态变换因子）广播发送到所有用户。对数据进行加密时，用户需要把对应于时刻t的累加值加入密文中，使其成为密文的组成部分，同时合法用户接收到广播消息后需要对各自私钥的可变部分进行更新（私钥中包含的证明值）。

4.2 算法描述

CKSE-SDS方案由6种基本算法构成，每一种算法都是被授权中心、广播加密方、广播加密接收方三方中的一方独立运行，授权中心为每一次加密维护一个撤销列表RL和状态集合ST。各算法描述如下。

Setup(1k,n) →(PP,MK,RL,ST)。Setup算法以安全参数k和能够支持的最大用户数量为输入。它输出一个公共参数PP，一个主私钥MK，一个撤销列表RL（初始为空），一个状态列表ST。该算法由授权中心运行。

PriKeyGen(PP,MK,S,ST) →(SKi,ST)。私钥生成算法以公共参数PP，主私钥MK，用户集合S和状态列表ST为输入。它输出一个私钥SKi和更新的状态列表ST。该算法由授权中心运行。

KeyUpd(PP,MK,t,RL,ST) →KUt。密钥更新算法以公共参数PP，主私钥MK，密钥更新时间t∈τ，撤销列表RL和状态列表ST为输入。输出一个密钥更新值KUt。该算法由授权中心运行。

DecKeyGen(SKi,KUt)→DKi,t。解密密钥生成算法以用户私钥SKi和私钥更新值KUt为输入。输出一个解密密钥DKi,t，如果用户i的私钥被撤销了，那么将会输出一个特殊符号⊥。

Enc(PP,S,t,K) →CTS,t。加密算法以公共参数PP、用户集合S、加密时间t和文件加密密钥（对称密钥）K∈κ（κ代表加密过程中用到的密钥空间）为输入。输出密文CTS,t。在私钥可撤销广播加密方案中，密文已经和时间周期关联起来。该算法由广播消息发送者运行，为简单起见，并且不失一般性，这里假设i、t均可以从密文CTS,t中快速计算出来。

KeyRev(i,t,RL,ST)→RL。密钥撤销算法以准备撤销私钥的用户的标识符i、撤销时间t、撤销列表RL和状态列表ST为输入，输出一个更新后的撤销列表RL，该算法也是具有状态的，由授权中心运行。

上述6种算法紧密配合，构成一个完整的广播加密系统，其正确性的内在要求为：对于Setup算法输出的PP和MK，K∈κ,i∈S,t∈T以及所有的可能状态列表ST和撤销列表RL，如果用户i的私钥在时间t没有被撤销，都能够以 1的概率得到Dec(PP,DKi,t,CTS,t)=K。

4.3 安全模型

基于 RSA累加器的密文密钥同步变换方案的安全模型被定义为在敌手和挑战者之间进行的一个博弈，过程如下。

1) 初始化。挑战者运行Setup算法生成一些公开参数PP，主私钥MK，一个撤销列表RL（初始时为空），一个状态列表ST。挑战者把PP发送给敌手A。

2) 查询。敌手A可以适应性地进行多项式个数的预言机查询（预言机之间共享了一些信息），包括以下预言机。

①私钥生成预言机：PriKeyGen(·)。挑战者选择一个标识符i为输入，利用其他公开信息调用预言机PriKeyGen(PP,MK,S,ST)，返回一个私钥SKi。

②密钥更新生成预言机：KeyUpd(·)。挑战者以时间t为输入，加上其他的公开信息调用预言机KeyUpd(PP,MK,t,RL,ST)，返回密钥更新值KUt。

③密钥撤销预言机：KeyRev(·)。挑战者以用户标识符i和时间t为输入，加上其他的公开信息调用密钥撤销预言机KeyRev(i,t,RL,ST)，输出一个撤销列表RL。

4) 猜测阶段。在博弈的最后阶段，敌手输出一个比特位b'。如果b'=b，那么敌手的攻击将会获得成功，以下限制必须成立。

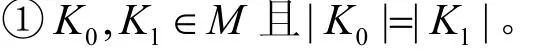
②在调用预言机KeyUpd(.)和KeyRev(·)时，查询的时间t必须大于或等于以前查询过的时间，即敌手只能以时间递增的顺序进行预言机的查询。同时，如果在时刻t已经对预言机KeyUpd(·)进行了查询，那么在这个时刻就不能对预言机KeyRev(·)进行查询。

③如果在标识符集合S*上查询了预言机PriKeyGen(·)，那么必须在 (S*,t)上对KeyRev(.)预言机进行查询，其中，t≤t*。

如果敌手输出的比特位b'=b，则返回值return设置为 1，否则设置为 0。由此可以定义敌手赢得博弈的概率为

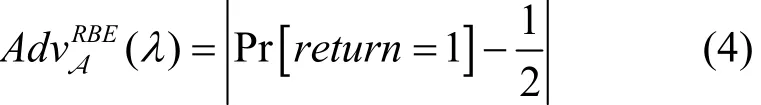
如果对于任意概率多项式时间的敌手A，(λ)对于安全参数λ都是可以忽略的，那么该方案就是CCA安全的。

4.4 方案构建

除了上述基本模块外，在构造过程中还需要一种具备基本安全功能的数字签名方案，该方案主要用在以下2个地方。

1) 授权中心在发布时刻t对应的累加器值时，必须对累加器值进行签名，确保累加器值的真实性，防止攻击者替换累加器值。

随着海上卫星通信技术的发展，越来越多的卫星通信系统将融入其中，各卫星系统均具备各自独特的优势。不同卫星服务供应商之间通过降低通信资费、提高通信技术抢占市场的局势也将成为可能。与MSC 97-19-6提案中提到的GPS/GLONASS/BDS联合接收设备相类似，各种组合式卫星通信设备已经面世，包括铱星-Inmarsat GX等。操作者可根据不同需求选择所需业务及系统，并有效降低操作负担。

2) 加密者对要发布的明文做一个签名，即为了达到CCA安全而采取的一个辅助措施。

在这2个地方，采用的签名算法都是统一的，签名私钥分别是授权中心和加密者对应的签名私钥。同时还需要一个扩碰撞散列函数，该函数能够把签名验证私钥映射到域Zp中，简化方案的构造。由于本文提出的 CCA安全的私钥可撤销密文密钥同步变换方案是建立在(n+1)-BDHE 假设上的，通过选择n−1个用户来描述整个系统的构建，使整个系统的安全性建立在n-BDHE假设之上，这与传统的方案相一致。然后利用一个函数把用户的身份标识符和时刻t映射成为索引i。具体构建过程如下。

Step1Setup(1k,n) →(PP,MK,RL,ST)

Setup算法首先准备公开参数。随机选择生成元g∈G， 选 择 随 机 值α,β,γ∈Zp， 计 算，同时设置v=gγ∈G，然后初始化算法准备和累加器相关的各个公开参数。

1) 该环节首先运行SigKeyGen算法产生一对公私钥(sk,pk)。这里使用普通的数字签名算法生成一对签名公私钥即可，随后用来进行签名生成与验证，如RSA。2) 计算i=1,2,… ,n,n+2,… ,2n。

3) 计算gβ∈G，U表示加入累加器中的元素构成的集合。在系统初始化阶段，U为空集，此时初始化算法把累加器值设为1，即ACφ= 1。同时设置初始状态列表STφ= {U,P1,… ,Pn,Pn+2,… ,P2n}，撤销列表在初始化阶段也是空的，这样全部的公开参数为其中，主私钥MK={α,β,γ,sk}。

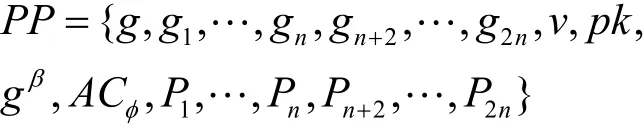
Step2PriKeyGen(PP,MK,S,STU) →(SKi,STU∪{i})

该算法为所有用户生成私钥，其中S代表所有注册用户组成的集合。定义V代表当前加入累加器中元素的记录信息集合，V是U的一个子集（随着系统的运行，部分用户私钥可能会被撤销）。注意，。私钥生成算法运算如下。

计算累加器集合中所有元素的证明值。更新累加值和相应的状态信息，使在集合S中的所有用户i，有

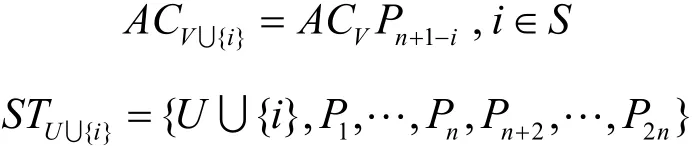
并选择一个随机数s∈Zp，最终生成的用户私钥＜K1,K2,K3＞ 为

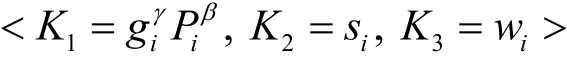
其中，K1和K2为固定部分，K3为可变部分（累加器集合中元素的证明值），并通过安全信道进行密钥分发。

在每个密钥更新周期开始的时刻t′，密钥更新算法通过执行以下步骤首先更新累加器。

从集合V中移除和l=φ(t) ∈ [n]相关联的所有元素，即移除所有和过期时刻t对应的被撤销用户的身份标识。其中，φ()是一个抗碰撞的散列函数，可将用户身份映射到集合[n]中，用于加密累加器中的元素计算，即i=φ(ID)。更新算法在累加器中使用新的周期t′并添加元素l′ =φ(t′ )∈ [n]，然后重新计算累加器的值使，即保证用户私钥的时间周期与密文中的时间周期一致。累加器的值ACV∪{l}及累加器集合元素证明值更新时计算步骤和PriKeyGen算法一样，然后为更新后的累加器值AC'V∪{l}生成签名σl。更新算法准备一个集合ΔV，包含了在最近一个更新周期中增加和移除的用户的身份标识符。然后更新算法把ΔV和KUt=＜AC'V∪{l},σl,wl＞作为广播消息发送给所有的用户。

Step4DecKeyGen(SKi,KUt)→DKi,t

解密私钥更新生成算法，由终端用户运行如下。

1) 计算并判断l(t)V=φ∈ 。

2) 利用公开参数中的签名验证公钥pk验证收到的累加器值AC'V上的签名lσ是否是合法的。

3) 计算并判断来确保收到的ACV是经过正确计算得来的。

设定一个布尔变量DecKeyChk。如果上述3个计算步骤中任何一个出现了错误，则赋值为 0；如果3个步骤均计算正确，则设置DecKeyChk为1。若DecKeyChk= 0，DecKeyGen算法输出一个特殊符号⊥，否则算法将证明值替换成最新的内容。计算证明值和解密私钥如下。

如果i∈V，且V∪Vw⊂U，计算

否则，输出一个特殊符号⊥，表示更新失败。然后设置更新后的用户解密密钥K2=si,K3=wi′ ＞ 。

Step5Enc(PP,M,ACV)→CTM,t

加密算法由广播加密消息发送方运行。其中M表示接收用户的标识符集合。算法首先调用SigKeyGen算法产生一对公私钥：一个签名私钥Ksig和验证密钥Vsig。为简单起见，假设Vsig∈Zp。设置KEY=e(g,gn+1)s∈G1，密文各构件计算如下

取Hdr=(CTM,t,Sign(CTM,t,Ksig),Vsig)。

Step6Dec(M,i,SKi,Hdr,PP)→KEY

根据 Step5所得结果，假设用户接收密文Hdr=((C0,C1,C2,C3),σ,Vsig)，解密算法过程如下。

1) 利用密钥Vsig验证σ是对密文的一个合法签名，如果签名不合法，则输出特殊符号⊥。

2) 选择一个随机数ω∈ Zp，然后计算

3) 解密密文

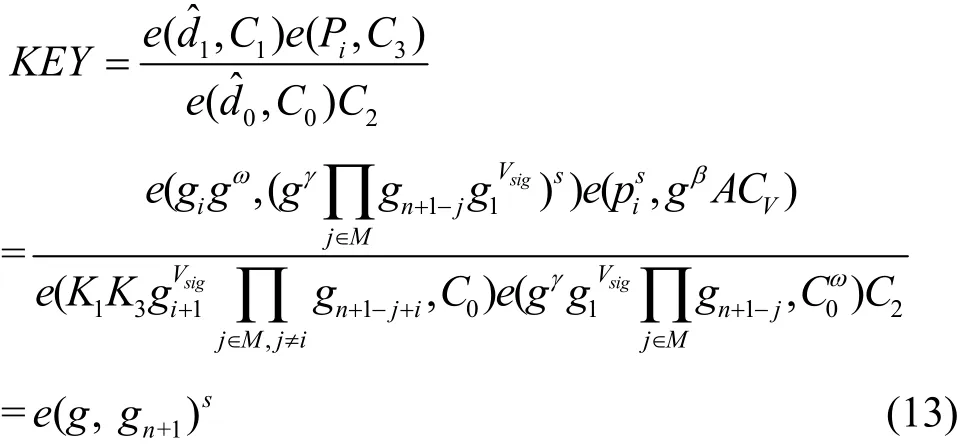
即当用户拥有合法私钥时，才能够解密密文获取数据加密密钥key。

5 安全性及性能分析

5.1 安全性证明

定理1G是一个具备素数阶p的双线性群，对于所有的正整数n，上述广播加密系统是CCA 安全的，假设判定(t,ε1,n)-BDHE 假设在群G中成立，Diffie-Hellman Exponent(n-DHE)假设成立，广播加密系统中采用的数字签名算法是(t,ε2,1)安全的，能够抵抗伪造攻击。

下面，通过 3个顺序变化的博弈 Game0、Game1、Game2完成广播加密方案安全性的证明。

Game0 Game0是一个和真实环境中攻击完全一样的博弈。

Game1 除了以下差别外，Game1和 Game0很类似。挑战者B收到一个随机的n-DHE向量，如果支持私钥撤销的广播加密方案不是 CCA安全的，那么挑战者B将能够利用攻击广播加密方案的敌手A，构造一个n-BDHE困难问题的解决方案。假设存在一个敌手A能够攻破广播加密方案的CCA安全性，那么挑战者B可以以ε1的概率解决n-BDHE困难问题。具体过程如下：当挑战者B收到一个n-BDHE挑战向量时，其中，Z的值可能是也可能是群G1中的一个随机元素。在Game1中，挑战者完成下述步骤。

Init 挑战者B调用敌手A，收到一个敌手希望进行攻击的用户身份标识集合S*。

Setup 挑战者B需要生成公开参数PP，并且为i∉S*的用户生成私钥di。算法B首先SigKeyGen

i算法获得签名私钥和验证密。然后，挑 战者选 择 一 个 随 机 值γ∈Zp， 设 置，同时还选择随机值α,β,γ∈Zp，计算Pi=gγ，设置ACφ= 1，公共参数，然后把公共参数发送给敌手A。注意，由于g、γ、α均是随机均匀地选择出来的元素，所以上述提供给敌手A的公开参数的分布情况和 Game0中的完全一致。敌手A需要所有不在目标集合S*中用户的私钥，所以挑战者B需要为其计算相应的私钥，计算过程如下

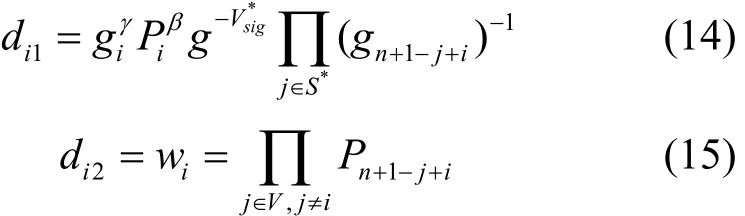
查询阶段 1 当挑战者B收到敌手A发出的密钥更新的查询后，B利用当前集合U和V，计算新的累加器值，利用私钥sk生成一个累加值的签名σj，然后B发布＜ACV,σj,wj＞，其中，wj是更新后的证明值。敌手A发出解密查询，以 ＜u,S,Hdr＞作为一个解密查询实例，其中挑战者B响应如下。

1) 调用算法Verify，利用密钥Vsig检查对生成的签名的有效性，如果签名是无效的，那么B输出特殊符号⊥。

2) 如果，挑战者B输出一个随机比特值，然后放弃模拟。

3) 如果密钥不相等，B选择一个随机值r∈Zp，然后计算

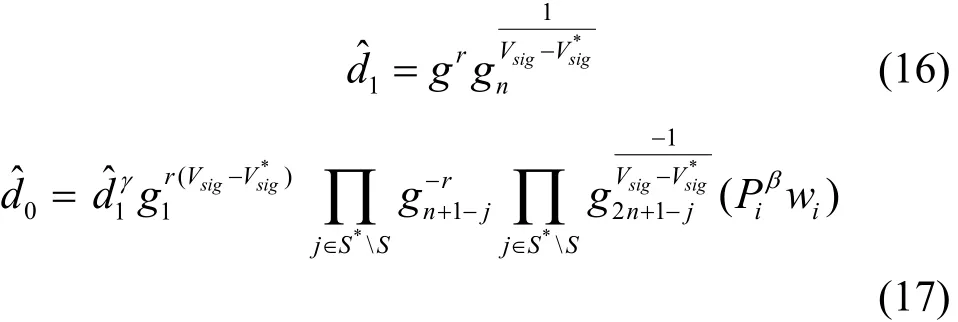
如果定义，那么可得

由于r是从Zp中随机选取的，r~在Zp中同样是随机的。因此挑战者B的响应和真实的解密调用Decrypt(S,u,du,Hdr,PP)是相似的，所以从整体来看，B的响应均和真实攻击博弈中的分布一致。

Challenge 为了生成合法的挑战消息，B设置其中，然后计算

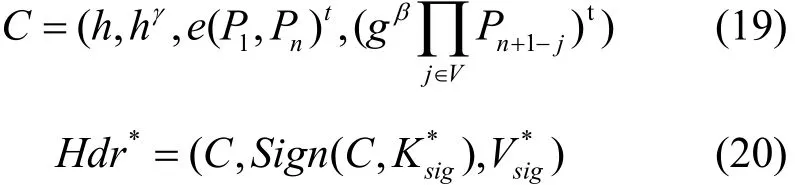
B随机选择一个比特位b∈ {0,1}，然后设置Kb=Z，在群G1中选择一个随机数K1−b。B向敌手A发出 (Hdr*,K0,K1)作为挑战值。当B收到的n-BDHE 输 入 向 量 中Z=e(gn+1,h)， 那 么(Hdr*,K0,K1)将会是一个合法的挑战值，和真实攻击中的一样。下述计算过程表明了这一论断。

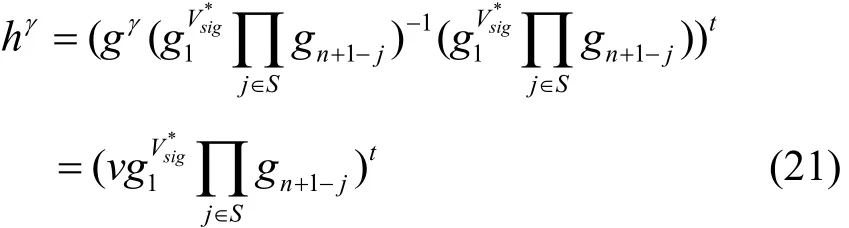
根据定义，)是一个对数据加密密钥e(gn+1,g)t加密的一个合法密文。更进一步讲，。因此，可以得出 (Hdr,K0,K1)对于敌手A来说是一个合法的挑战值。另一方面，当Z是群G1中的一个随机元素时，K0、K1也是G1中的随机元素。

查询阶段2和查询阶段1中完全一致，在此不再赘述。

Guess 敌手A输出一个对比特位b的一个猜测，如果b0=b，那么挑战者B输出 0，表明，否则，B输出1，表明Z是群G1中的一个随机元素。如果向量是从BDHER中提取出的，那么。如果以abort代表挑战者B在模拟过程中出现的退出事件。那么当向量是从PBDHE中提取出来的，将会得到

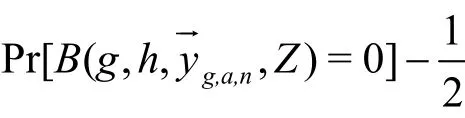
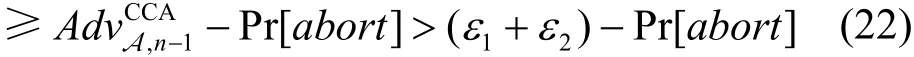
第一个不等式说明，当提取出来时，B进行的模拟是完美的，B也不会出现退出现象。由此可以得出B以(ε1+ε2) − Pr[abort]的 概 率 解 决n-BDHE困 难 问题。可以得出 Pr[abort]＜ε2。如果不是这样，那么可以通过调用敌手A以最少ε2的概率伪造一个合法签名。此时，可以构造另外一个模拟器，正在完成一个存在性伪造博弈，在知道私钥γ的情况下，收到了挑战消息。在上述挑战实验中，敌手可以通过提交一些查询，该查询包含了一个对某些密文构造了一个存在性伪造签名，这样的查询可以导致挑战者退出。挑战者就可以利用这个伪造签名赢得存在性伪造博弈。在这样的博弈中，敌手只生成了一个选择消息查询来生成挑战密文中需要的签名。由此可以得到Pr[abort]＜ε2。挑战者B解决困难问题的优势最少是ε1。至此，完成了Game1。

Game2 挑战者B能够访问一个签名预言机Oσ，获得了一个作为输入的签名验证密钥pk，一个双线性对的公开参数(q,G,G1,ε,γ,η)，一个n-DHE假设 的 实 例， 其 中 ，挑战者B需要计算Pn+1。挑战者按照以下步骤进行。首先，随机选择α,β,γ∈Zp，然后，B用设置ACφ= 1，生成公私钥对＜pk,sk＞，并将公开参数发送给敌手A。当敌手要求用户i的私钥时，挑战者B计算di,1和di,2的方法和 Game1中的完全一样。接下来，B为敌手A准备密文，随机地选择一个元素t∈Zp，然后计算

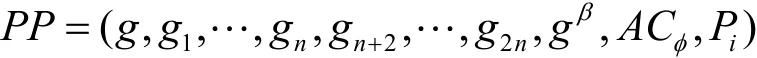
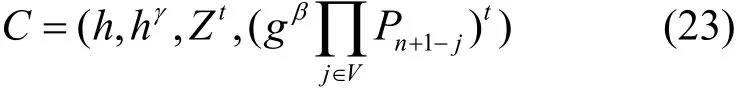
如果B的输入Z是e(P1,Pn)，那么送给敌手A的密文是一个合法的密文；如果Z是随机元素，那么密文也是一个随机值。如果敌手能够区分这2个密文，那么它将能够成功地伪造一个有效的证明值，这样即使i∉VO，攻击者仍然可以进行解密密钥更新，从而绕过累加器机制的验证。然后挑战者B可以计算，如果和Pi不对应，那么敌手一定攻击了累加器值的签名，将会是一个伪造的签名。否则B可以根据累加器的验证等式计算出Pn+1，即

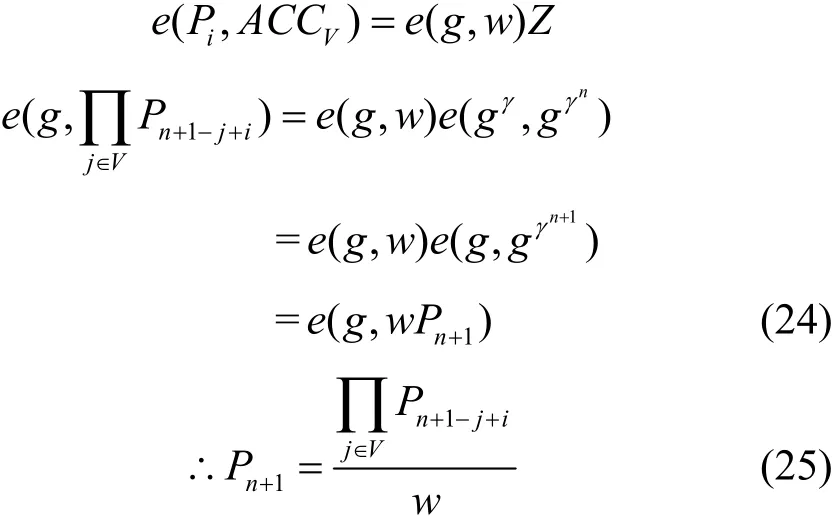
于是，挑战者B攻破了n-DHE困难问题。

上述3个在敌手和挑战者之间进行的博弈，即可以完成对定理1的证明。因此，本文提出的基于RSA累加器的支持密文周期性演化的广播加密方案是CCA安全的。

5.2 性能分析

本节着重从通信开销及计算开销 2个方面对CKSE-SDS方案的用户私钥撤销及密文演化过程性能代价进行分析，并就静态密文及密文演化情形下攻击者通过获取密文密钥进行密文破解的概率进行对比分析。首先定义性能分析中的符号含义如表1所示。

表1 符号含义

5.2.1 私钥撤销开销分析

CKSE-SDS方案通过使用密码学累加器维持一个可解密的用户列表。用户私钥撤销时，只需将该用户的身份标识对应的元素值从列表中去除即可，由此基于用户密钥的灵活管理实现存储数据的高效共享。相关参与方通信及计算开销分析对比如下。

首先，密钥管理中心计算累加器集合中更新元素的证明值，计算开销为nc。然后对原累加值进行替换并对密文重新签名，分别需要进行一次乘法运算、幂运算及数字签名，计算开销为exp+c+sig，通信开销为2|G|+|δ|。在该过程中，密文更新不需要资源提供方参与，计算开销可记为0；用户私钥更新时，只需对该用户私钥中的证明值（即私钥构件K3）进行更新，计算开销较小，为常量O(1)；而被撤销用户身份标识不在当前周期的累加器列表中，故无法使用收到的其他用户的证明值对自身私钥进行更新。数字签名过程虽然增加了用户的计算开销，但能够抵抗伪造攻击（见5.1节定理1证明），从安全性的角度考虑，在传输过程中增加该环节是必要的。本文方案和相关方案对比如表2所示，包括通信开销、私钥更新过程密钥管理中心计算开销及密文更新过程客户端计算开销 3个部分。

表2 私钥撤销过程通信及计算开销比较

从表2可以看出，用户私钥撤销时，通信开销和其他方案相比基本持平，在可接受范围内。但对于密文更新而言，一般方案（如文献[22,24]）均采用的数据重加密实现，计算开销大。而CKSE-SDS方案通过引入密码学累加器构造的密文密钥拟态变换因子，有效支持密文密钥的动态分割与融合，使密文密钥的更新只需进行关键构件的替换即可，且对于密钥更新而言，更新开销为乘法运算，远小于列表中方案的群元素幂运算，从而有效降低了更新过程的计算开销，保证了方案运行的高效性。

5.2.2 密文演化开销分析

如前所述，CKSE-SDS方案将密码学累加器应用到支持安全数据共享的广播加密中。密文在新的周期时刻t′演化时，用户只需将原密文中的累加值替换为新生成的对应于时刻t′的累加值并生成新的签名，其他密文构件不变，极大减少了数据重加密带来的计算开销。该过程相关参与方通信开销及客户端计算开销分析如下。

密钥管理中心将周期t′映射后的元素加入累加器集合并重新计算，开销为nc，所需通信开销为 2|G|+|δ|；重新计算集合中元素对应的证明值所需开销为(n2–1)c，通信开销为n|G|；同时，密钥管理中心可直接对原累加值进行替换并对密文重新签名，分别需要进行一次乘法运算、幂运算及数字签名，计算开销为exp+c+sig。

本文方案和相关方案对比如表3所示，虽然在密文演化过程中通信开销有所增加（开销与群元素大小成正相关，且至多为保留解密权限的累加器集合元素数量，仍在可接受范围内），但该过程不需要客户端参与计算（开销可记为0），能够有效地缓解资源提供方的计算负担，对于计算能力较弱的移动设备尤其适用。

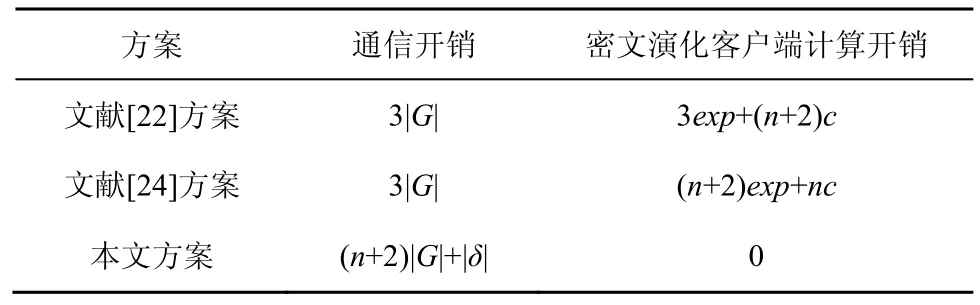
表3 密文演化中通信与计算开销比较

5.2.3 基于密文演化的攻击概率分析

接下来，对静态密文及周期性密文演化情形下攻击者攻击成功的概率进行分析。

记密文密钥同步变换的周期为t，假设在较长时间内攻击者获取密文ci、用户私钥

以及该用户对应的代理解密密钥的概率分别为和，则在时间t内攻击者获取密文ci、用户私钥ki以及代理解密密钥dki的概率分别为和， 显 然 有。定义时间τ内攻击者获取密文ci后直接破解成功的概率为Pdci，则在t内获取密文ci后直接破解成功的概率为P'dci＜Pdci。下面，讨论以下情形。

1) 静态密文

此时，记攻击者在较长时间段τ内对密文ci破译成功的概率为Pw，这一概率包括获取密文ci并直接破解成功的概率以及同时获取密文ci、用户私钥ki以及代理解密密钥dki的概率 2个部分，这里记为。基于 Diffie-Hellman Exponent假设在一般群模型中的困难性[25]，Pdci部分可以忽略不计。

2) 密文周期性演化

单周期t内，攻击者对某密文ci破译成功的概率记为，此阶段密文状态不发生变化。

对于时间τ内的n次密文演化（τ=nt），获取密文ci并直接破解成功的概率仍记为；由于只有密文密钥处于相同时间周期才能完成解密操作，因此，通过获取密文密钥实现密文解密的概率记为。综上，密文演化情形下攻击者获取c i并解密成功的概率为。同理，Pdci可以忽略不计，显然有Pnw＜Pw。

在静态密文及密文周期性演化情形下，攻击者通过利用系统安全漏洞获取密文、密钥进行密文破解的概率统计如表4所示。

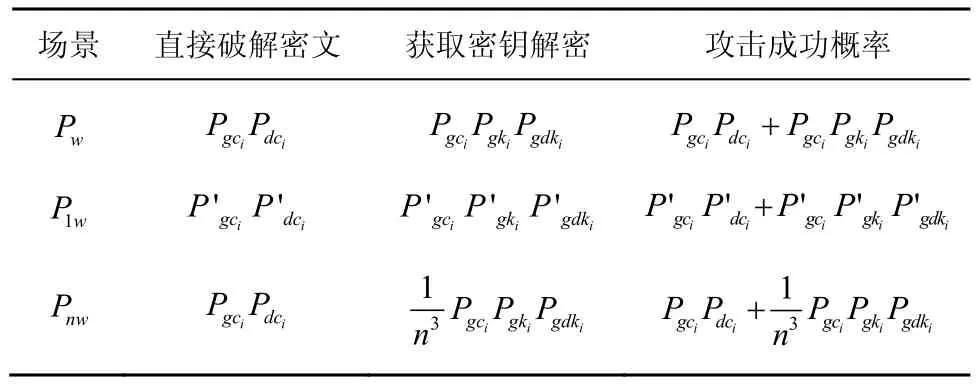
表4 攻击概率对比

综上分析，在较长时间内攻击者通过某种攻击方式获取到存储密文及某用户私钥，若该密文密钥不在同一个时间周期，则无法完成解密，从而使攻击结果无效。因此，当云存储中的密文进行周期性演化时，系统能够通过增加攻击者的时间成本，有效降低攻击者通过获取密文密钥来破解用户私密信息的概率。

6 结束语

针对云存储系统加密机制的静态特点，本文将密码学累加器技术引入广播加密中，通过密文密钥的动态分割与融合设计了CKSE-SDS方案，有效解决了因静态密文存储导致的攻击者易通过获取密钥破解密文的问题，为提升加密云存储系统的主动安全防御能力提供新的方法；同时基于拟态变换因子实现密文密钥关键构件的可替换更新，解决了传统方案中基于密钥分发和重加密实现密文密钥更新带来的计算开销大的问题。理论分析及安全性证明表明，CKSE-SDS方案能够实现安全有效的数据共享并支持高效的密文密钥同步演化，有效降低了攻击者攻击成功的概率。

[1] 苏金树, 曹丹, 王小峰, 等. 属性基加密机制[J]. 软件学报, 2011,22(6)∶1299-1315．SU J S, CAO D, WANG X F, et al. Attribute-based encryption schemes[J]. Journal of Software, 2011, 22 (6)∶1299-1315.

[2] 冯登国, 张敏, 张妍,等. 云计算安全研究[J]. 软件学报, 2011,22(1)∶71-83.FENG D G, ZHANG M, ZHANG Y, et al. Study on cloud computing security[J]. Journal of Software, 2011,22(1)∶71-83.

[3] 黄刘生, 田苗苗, 黄河. 大数据隐私保护密码技术研究综述[J]. 软件学报, 2015, 26(4)∶945-959.HUANG L S, TIAN M M, HUANG H. Preserving privacy in big data∶a survey from the cryptographic perspective[J]. Journal of Software,2015, 26(4)∶945-959.

[4] DAN B, FRANKLIN M K. Identity-based encryption from the Weil pairing[C]//International Cryptology Conference. 2001∶213-229.

[5] SAHAI A, WATERS B. Fuzzy identity-based encryption[C]// International Conference on Theory and Applications of Cryptographic Techniques. 2005∶ 457-473.

[6] 邬江兴. 网络空间拟态安全防御[J]. 保密科学技术, 2014(10)∶ 4-10.WU J X. Cyber minic security defense[J]. Secrecy Science and Technology, 2014(10)∶4-10.

[7] 邬江兴. 拟态计算与拟态安全防御的原意和愿景[J]. 电信科学,2014, 30(7)∶1-7.WU J X. Meaning and vision of mimic computing and mimic security defense[J]. Telecommunications Science, 2014, 30(7)∶1-7.

[8] 刘杰, 曾浩洋, 田永春,等. 动态弹性安全防御技术及发展趋势[J].通信技术, 2015(2)∶117-124.LIU J, ZENG H Y, TIAN Y C, et al. Technology and developmenttrend of dynamic resiliency for security defense[J]. Communications Technology, 2015(2)∶117-124.

[9] JAJODIA S, JAJODIA S, JAJODIA S, et al. moving target defense[J].Advances in Information Security, 2011, 54∶99-108.

[10] 蔡桂林, 王宝生, 王天佐,等. 移动目标防御技术研究进展[J]. 计算机研究与发展, 2016, 53(5)∶968-987.CAI G L, WANG B S, WANG T Z, et al. Research and development of moving target defense technology[J]. Journal of Computer Research and Development, 2016, 53(5)∶ 968-987.

[11] JAJODIA S, GHOSH A K, SWARUP V, et al. Moving target defense∶creating asymmetric uncertainty for cyber threats[J]. Springer Ebooks,2011.

[12] WANG H, JIA Q, Dan F, et al. A moving target DDoS defense mechanism[J]. Computer Communications, 2014, 46(6)∶10-21.

[13] 雷程, 马多贺, 张红旗,等. 基于最优路径跳变的网络移动目标防御技术[J]. 通信学报, 2017, 38(3)∶133-143.LEI C, MA D H, ZHANG H Q, et al. Network moving target defense technique based on optimal forwarding path migration[J]. Journal on Communications, 2017, 38(3)∶133-143.

[14] 罗兴国, 仝青, 张铮,等. 拟态防御技术[J]. 中国工程科学, 2016,18(6)∶69-73.LUO X G, TONG Q, ZHANG Z, et al. Mimic defense technology[J].Engineering Sciences, 2016, 18(6)∶69-73.

[15] 仝青, 张铮, 张为华,等. 拟态防御Web服务器设计与实现[J]. 软件学报, 2017, 28(4)∶ 883-897.TONG Q, ZHANG Z, ZHANG W H, et al. Design and implementation of mimic defense Web server[J]. Journal of Software, 2017, 28(4)∶ 883-897.

[16] YU S, WANG C, REN K, et al. Attribute based data sharing with attribute revocation[C]//ACM Symposium on Information, Computer and Communications Security. 2010∶261-270.

[17] HUR J, DONG K N. Attribute-based access control with efficient revocation in data outsourcing systems[J]. IEEE Transactions on Parallel & Distributed Systems, 2011, 22(7)∶1214-1221.

[18] ZU L, LIU Z, LI J. New ciphertext-policy attribute-based encryption with efficient revocation[C]//IEEE International Conference on Computer and Information Technology. 2014∶281-287.

[19] YANG K, JIA X, REN K. Attribute-based fine-grained access control with efficient revocation in cloud storage systems[C]//ACM Sigsac Symposium on Information, Computer and Communications Security.2013∶523-528.

[20] XIA Z H, ZHANG L G, LIU D D, et al. Attribute-based access control scheme with efficient revocation in cloud computing[J]. China Communications, 2016, 13(7)∶92-99.

[21] FIAT A, NAOR M. Broadcast encryption[M]//Advances in Cryptology— CRYPTO’ 93. Springer Berlin Heidelberg, 1993∶480-491.

[22] PHAN D H, POINTCHEVAL D, SHAHANDASHTI S F, et al. Adaptive CCA broadcast encryption with constant-size secret keys and ciphertexts[J]. International Journal of Information Security, 2013,12(4)∶251-265.

[23] ZHOU Z, HUANG D, WANG Z. Efficient privacy-preserving ciphertext-policy attribute based encryption and broadcast encryption[J].IEEE Transactions on Computers, 2014, 64(1)∶126-138.

[24] WU Q, QIN B, ZHANG L, et al. Contributory broadcast encryption with efficient encryption and short ciphertexts[J]. IEEE Transactions on Computers, 2016, 65(2)∶466-479.

[25] BONEH D, BOYEN X, GOH E J. Hierarchical identity based encryption with constant size ciphertext[C]//International Conference on Theory and Applications of Cryptographic Techniques.2005∶440-456.