可调整个体优先级的双边匹配算法

王彦博，于瀚辰，沈体雁

WANG Yanbo,YU Hanchen,SHEN Tiyan

北京大学 政府管理学院，北京 100871

School of Government，Peking University，Beijing 100871，China

1 相关文献综述

大多数情况下经济学家都简单假定“市场”能够直接产生竞争均衡的价格，但在器官匹配、学生择校等领域，基于道德、社会习惯、公平性等方面的考虑，无法将资源完全商品化，从而无法完全由价格决定最后的分配结果，因此需要对交易规则进行充分设计以达到某种最优目标[1-2]。“市场设计学”在20世纪90年代之后逐渐成为一个严谨的科学分支，从这一时期开始经济学家获得了对复杂市场（尤其是公共资源分配市场）进行设计的机会，并在实践上获得巨大成功，最知名的案例是1996年由Roth主导重新设计的美国住院医生实习系统以及1994年由McAfee等人设计的美国收音频谱拍卖系统，他们对现存市场各方面的细节问题做深入考察，抽象出基本的模型假设，并提供一组可行的制度安排，提高了市场效率[3-5]。

市场设计最成功的实践案例都发生在拍卖市场和匹配市场。其中匹配市场设计的理论基础为匹配理论（Matching Theory），主要研究离散不可分资源的匹配、分配、交换问题，核心工作是匹配算法的设计以及算法稳定性、帕累托有效、策略行为免疫等相关性质的证明，其中又以稳定性最为重要[6-7]。匹配理论的创始人是Gale和Shapley，他们在1962年探讨了一对一的婚姻匹配问题和一对多的大学招生问题，建立了基本的双边匹配模型，提出延迟-接受算法（亦常被称为G-S算法），并证明该算法总存在稳定结果，此后国内外学者围绕匹配模型展开大量研究[8-9]。近年来对双边匹配算法的理论探讨主要集中于个体行为假设的变形以及匹配模型的扩展，如Klumpp将线性空间模型引入了双边匹配问题[10]，Erdil讨论了个体偏好序非严格情况下的稳定匹配[11]，Castillo讨论了参与主体采取截短策略时的风险和收益[12]。匹配理论的繁荣发展促进了市场设计学在劳动力就业、高校录取、定向广告、电子商务、人力资源、金融等多个领域的应用[13-17]。

机制设计、拍卖理论、匹配理论等工具常被用于分析既定规则下市场参与者的均衡行为，但因现实市场环境过于复杂，常常无法获得理论上的解析解，因此还需要计算模拟、心理实验等方法作为补充，Roth将这一综合方法称之为“经济工程学”[3]。Roth于1996年受邀重新设计NRMP匹配算法以解决由于学生情侣增多而导致的NRMP参与率逐年下滑问题，在算法设计和评价过程中，他使用1993—1995年间NRMP参与者的真实偏好数据以及随机生成的偏好数据进行大量仿真模拟，新的Roth-Peranson算法于1998年正式在NRMP投入使用，重新提升了NRMP的参与率，成为模拟实验与理论分析互补达成市场设计的成功范例[18]。Shapley和Roth也由于“稳定匹配理论和市场设计实践”而获得了2012年诺贝尔经济学奖。

2 传统双边匹配算法存在的问题

无论是G-S算法，还是NRMP采用的Roth-Peranson算法，都存在以下问题[4，18-20]：（1）单边占优问题，率先发出申请的一方总体效用优于被动接受申请的一方。（2）缺乏最低保障，部分参与者效用可能会极差。（3）缺乏灵活调控空间，算法最多只能产生两个稳定匹配结果，即参与双方某一方占优的结果，而无法细致调节每一个参与主体的优先顺序。

以学生和医院匹配为例，G-S算法必须首先选择学生或医院中的某一方作为申请方，申请方按照自己的偏好顺序从优到次向心仪的对象发出申请，收到申请的一方选择接受或者拒绝。这种设计能够保证得到稳定匹配结果，但匹配流程优先照顾申请方的偏好，因此导致申请方整体效用比被申请方高[8]。模拟100个学生和100个医院的一对一匹配，为每个学生和医院随机生成长度为100的偏好序，图1展示了G-S算法匹配结果的偏好位序累积情况，图中横坐标表示最终被匹配到了偏好序中第几位的对象，纵坐标表示累计的匹配数量，例如学生匹配结果曲线中的一个点（X=3,Y=12）表示有12个学生最终被匹配到了其偏好序中前3位的医院，曲线越凸意味着效用越高。当设定学生为申请方时（图1（a））大多数学生都匹配到了其偏好序中前15位的医院，全部学生都匹配到了其偏好序中前40位的医院，该算法对于学生是最优的稳定匹配；但有相当一部分医院匹配到了其偏好序中40位之后的学生，甚至部分医院匹配到其偏好序中70位之后的学生，该算法对于医院来说是最差的稳定匹配。反之当设定医院为申请方时（图1（b）），结果对医院最优，对学生最差。可见G-S算法会使得整体上某一边比另一边更占优，且部分参与主体的效用极差。

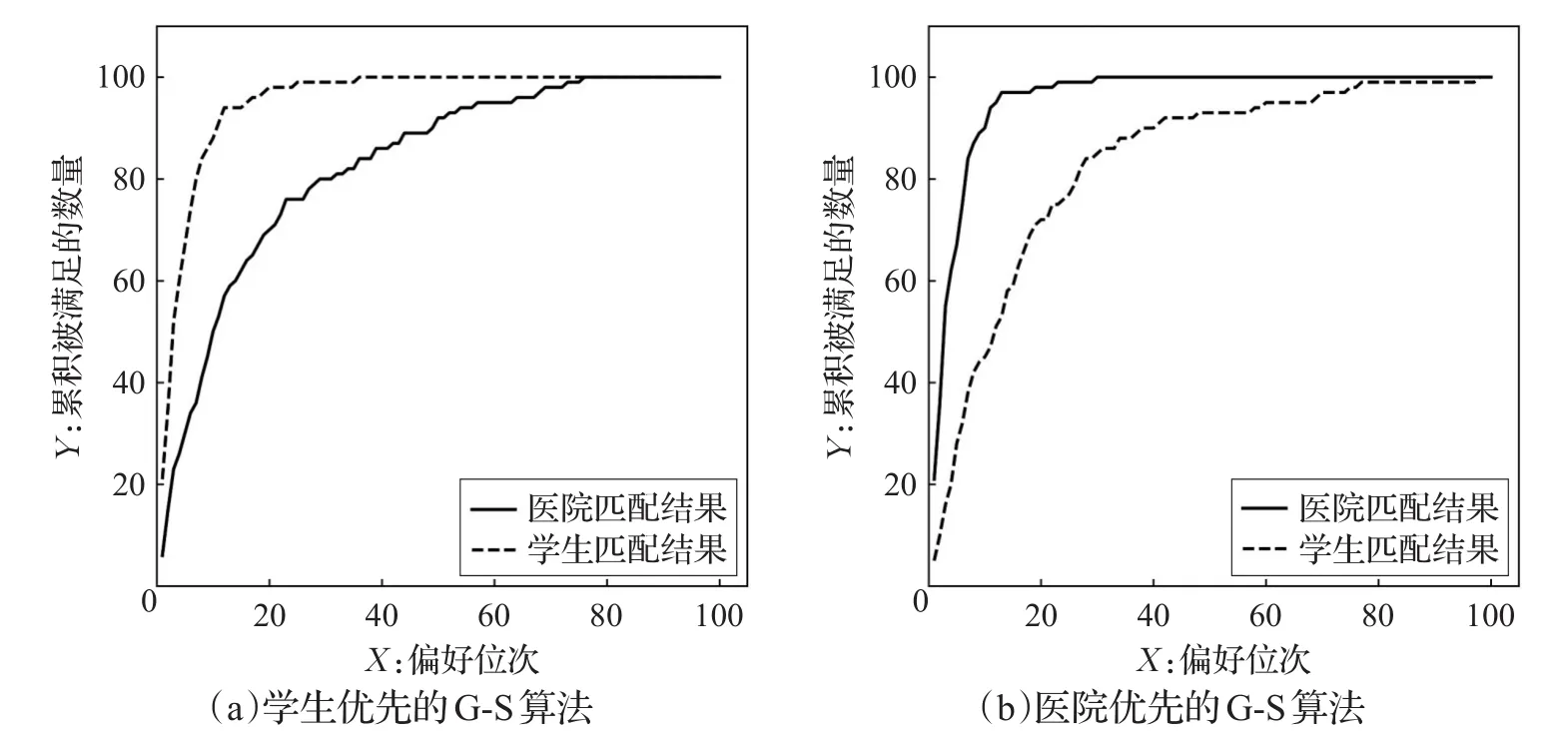
图1 G-S算法的偏好位序满足累积曲线

Roth发现住院医生实习市场中稳定匹配集合的基数很小，即无论哪方率先发出申请，得到的匹配结果相差不大，这主要是因为该场景中参与主体对于各自的优劣排名认知较为一致，即每个医院对毕业生的偏好相似度很高，同时每个毕业生对于医院的偏好相似度也很高[4，21]。但是婚姻匹配等众多双边匹配问题中，参与主体的偏好差异性很大，稳定匹配集合的基数也会随之增大，G-S算法的单边占优以及缺乏最低保障等问题就会凸显，使得匹配结果较差的参与者积极性下降，降低市场厚度，进而导致市场设计失败[21]。实际上即使在单边占优问题并不严重的住院医生实习市场，NRMP采用医院优先的匹配算法也曾招致大量学生表达不满甚至退出NRMP匹配系统，因此如何提高效用较差者的满意度成为决定市场设计成败的关键问题[3]。李铭洋、樊治平等关注到这一问题并提出了解决方案，将双方主体匹配序值之和最小作为目标构建了多目标优化模型，使得结果不再偏向于某一方，解决了单边占优问题[22]。但该方法并不能给予效用最差者以最低保障，仍然可能有个别参与主体效用过差，因此在维护市场厚度方面尚存在改进空间，另外其方案也只能调整参与匹配某一方整体的优先级，而无法针对某个参与个体做出调整。

为了更好地解决单边占优问题、最低保障问题以及提供灵活调控个体优先级的机制，本文提出了WYS算法。

3 WYS算法

一个典型的双边匹配问题中包含两类主体集合，以医学毕业生就业市场上医院与学生的匹配为例，有学生集合S={S1,S2,…,Sn}和医院集合H={H1,H2,…,Hm}，每个学生Si试图寻找一个医院签约工作，每个医院Hj试图招聘qj个学生。每个学生Si对其可接受的医院，以及每个医院对其可接受的学生，都有一个完备的、可传递的、严格的偏好序。匹配结果为S×H的一个子集M，M中的每个元素是一个学生和一个医院的匹配对，在M中每个学生只出现不超过1次，每个医院出现不超过qj次。匹配结果稳定意味着M中不存在阻碍对（blocking pairs），一个好的双边匹配算法总能找出稳定的匹配结果。

WYS算法将学生和医院都视为实体（Entity），全体学生和医院构成的集合称为实体全集ES。对于任一实体E来说，与E不同类型的实体称之为对手实体。例如对一个医院实体来说，所有的学生实体是对手实体。每个实体E拥有以下属性（实体的属性可以使用“E.属性名”的方式来表示）：

（1）优先级R：外生给定ES一个全序，用正整数表示，E.R为实体E对应的正整数，E.R越大意味着E的优先级越高。

（2）偏好序P：每个实体E都有一个描述自己对于对手实体偏好程度的严格序列，在偏好序中越靠前则意味着越希望与对方匹配。例如某学生S1最心仪的医院是H3，其次是H5，再次是H1，该学生只考虑与该偏好序中的医院签约，不考虑其余医院，则S1.P={H3,H5,H1}。用E1.P(E2)＞E1.P(E3)表示在E1的偏好序中E2排在E3之前。

（3）匹配容量C：E能够匹配的对手实体数量。例如某医院E1欲招聘4个学生，则E1.C=4。在就业市场中，学生类型实体的容量恒为1，医院类型实体的容量由每个医院根据招聘计划自定。

（4）已匹配列表M ：目前暂时与E匹配的对手实体列表。在算法运行过程中每个实体E的E.M都会不断迭代更新，算法停止时E.M中的实体即为E的最终匹配对象。当E.M中的实体数量等于E.C时，称“E已匹配满”。

（5）最差实体WME（Worst Matched Entities）：E.M中最不被E偏好的实体。算法运行过程中E.WME会随着E.M的变化而不断更新。

WYS算法维护一个无序集合L和一个有序队列T。初始时将ES中所有实体都加入L，将T置空，然后启动第一轮外层循环，循环过程中会不断调用Apply函数，每次调用Apply函数都意味着某个实体向另一个实体发出了匹配申请，在Apply执行过程中有可能解除某些暂时的匹配，被解除匹配的实体会被放入T中，下一轮循环优先让T中的实体发出申请。算法框架参考图2，算法具体细节参考伪代码及注释。

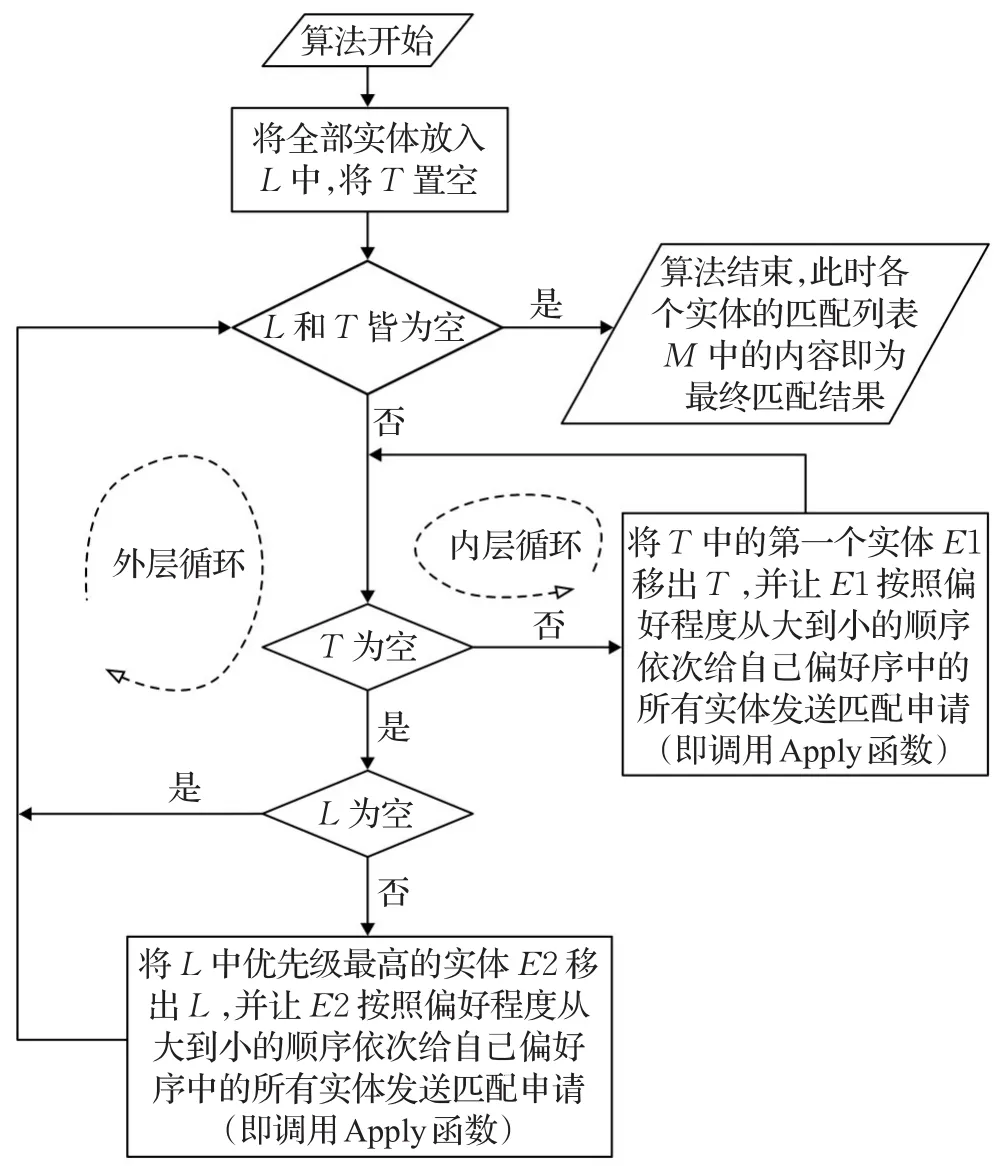
图2 WYS算法框架

WYS算法伪代码

WYS算法注释

2：只要L和T任何一个非空，就不断进行外层循环。

3：只要T非空，就不断进行内层循环，每次循环都从T中取出一个实体处理。

4：将T中排第一位的实体移出T，并将该实体作为变量E1。

5～7：E1按照偏好程度从大到小的顺序依次向其偏好序中的实体发出申请，即调用Apply函数，Apply函数的具体定义见下文伪代码。

9：判断L是否为空，若不为空就从L中取出一个实体处理。

10：将L中R值最大的实体移出L，并将该实体作为变量E2。

11～13：E2按照偏好程度从大到小的顺序依次向其偏好序中的实体发出申请。

15：算法结束，此时每个实体E的匹配列表E.M中的结果即为最终匹配结果。

Apply(E1,E2)函数定义伪代码

Apply函数注释

1～3：若E1不在 E2.P中，或 E2不在E1.P中，则E1和E2不可能匹配，直接结束函数。

4～6：若E1对于E2来说还不如E2已匹配的最差者，或E2对于E1来说还不如E1已匹配的最差者，则E1和E2不可能匹配，函数直接结束。

7：创建一个空的、有序的临时队列变量，命名为tmp_list。

8：若E1已匹配满，则解除E1和E1.WME的暂时匹配状态，并进行其他相关处理。

10～11：解除E1和E1.WME的暂时匹配状态。

12～14：若实体w1曾发出过至少一次申请且w1目前不在T中，则将w1放入临时队列tmp_list中。

16：若E2已匹配满，则解除E2和E2.WME的暂时匹配状态，并进行其他相关处理。

17～19：解除E2和E2.WME的暂时匹配状态。

20～22：若实体w2曾发出过至少一次申请且w2目前不在T中，则将w2放入临时队列tmp_list中。

24：按照R值从大到小的顺序对tmp_list中的实体进行排序。

25～27：将tmp_list中的实体依序插入T中，插入每一个实体时若T非空，就将该实体插到T中现存的最后一个实体之前（这是为了保证最新被踢掉的实体在T中排在最前列，从而下一轮循环中可以率先尝试发出申请）。

28～29：将E1和E2互相加入对方的暂时匹配列表中，E1和E2暂时成为互相匹配的实体。

4 实验结果及讨论

图3 10次随机实验平均的医院与学生偏好位序满足累积曲线

进行与第2章中相同的随机实验10次，分别用医院优先的G-S算法、学生优先的G-S算法和WYS算法对100个学生和100个医院在随机偏好序下进行匹配。其中WYS算法需要先设定优先级R，优先级高的实体会优先发出申请并在最终匹配结果中相对占优。实验中参考对手实体的偏好序来确定优先级R，将学生和医院按照被偏好程度从大到小排序，占据医院偏好序中第一名最多的学生为学生队列的第一位，若两学生占据医院偏好序中第一名数量相同则根据占据医院偏好序中第二名的数量排位，以此类推，对全体学生进行优先级排序，医院排序采用同样方法操作。学生队列排序结果为{SR1,SR2,…,SR100}，医院队列排序结果为{HR1,HR2,…,HR100}，设定优先级结果为 SR1.R＞HR1.R＞SR2.R＞HR2.R＞…＞HR100.R。理论上优先级可以随意设置，优先级越高的实体最终越占优，不同的优先级设定可能会产生不同的匹配结果，上述设定方式符合“最受欢迎者优先”的一般常理。通过实验可知WYS算法解决了第2章提出的传统算法存在的问题。

（1）WYS算法非单边占优。图3（a）展示了10次随机实验医院的平均匹配结果：G-S算法中优先发出申请一方的效用明显好于另一方，而WYS算法的结果对于医院和学生没有明显倾向性，多数参与主体都匹配到了其偏好序中前30位的对象，不会使某一方达成最差的稳定匹配。G-S、Roth-Peranson等传统算法中的劣势一方由于只能被动选择接受或拒绝，其自身偏好序中的部分对象永远没有机会尝试匹配，理论上存在改善其效用的空间[23]。WYS算法为参与匹配的双方主体设定一个外生优先级，让全部主体按照优先级依次发出申请，每个主体都有机会遍历自身偏好序中的全部对象，只要设置合理的优先级，就可使得匹配双方被同等对待。

（2）WYS算法提高了G-S等传统算法中效用最差者的满意度。如表1所示，10次随机实验中WYS算法的2 000个参与主体没有任何一个匹配其偏好序67位之后的对象，而G-S算法匹配到偏好序67位之后的主体数量为41（学生优先）和33（医院优先），WYS算法在偏好序位次30～100，40～100，50～100范围内匹配成功的主体数量也都明显少于G-S算法，即效用过差者的数目有显著减少。图4展示了10次实验中2 000个主体匹配结果的偏好位序分布情况，相对于G-S算法，WYS算法的过大异常值数目明显较少且异常值的整体位序值不高，箱线图上边缘和上四分位较低，下四分位和中位较高，整体来看WYS算法上下四分位之间的分布较为集中。WYS算法相对于G-S算法来说牺牲了很少一部分效用极高者的利益，换取了效用最差者结果的显著提升。

表1 10次实验中2 000个主体匹配结果的偏好位序统计

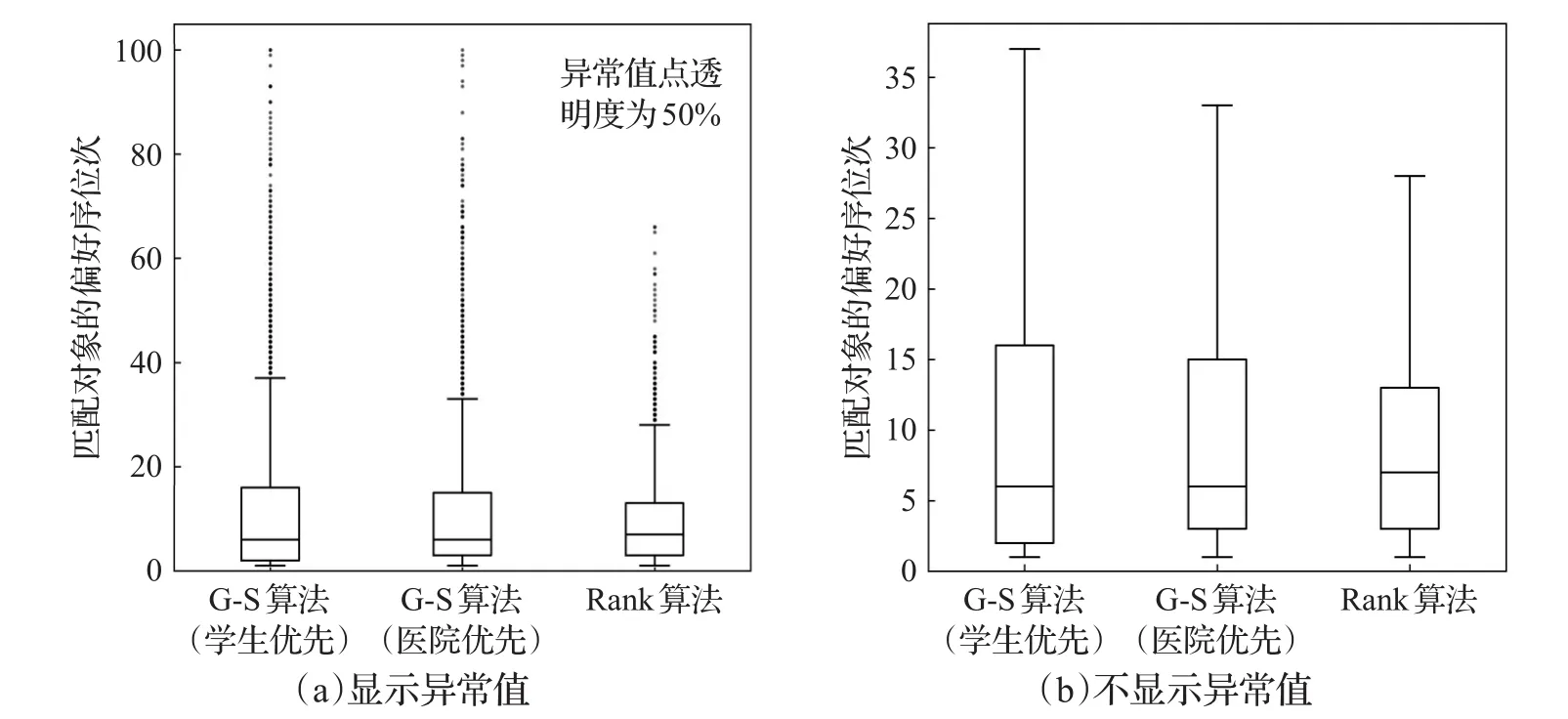
图4 10次实验中2 000个主体匹配结果的偏好位序分布箱线图

（3）WYS算法提升了参与者的总体效用。图5为10次实验平均之后的学生和医院整体匹配结果偏好位次累积曲线，其中WYS算法曲线最凸，两种G-S算法的曲线几乎重合，较WYS算法更为平缓，意味着WYS算法的整体效用比G-S算法更高。WYS算法平均有191个主体匹配到了其偏好序中前30位的对象，有196.8个主体匹配到了其偏好序中前40位的对象，优于G-S算法的匹配结果。实验过程中生成偏好序的方式为0～1 000之间随机打分，打分高者在偏好序中排名靠前，若以匹配对象的打分值作为主体获得的效用，则WYS算法、学生优先的G-S算法和医院优先的G-S算法给出的每个参与主体的平均效用分别为902.5、877.4和878.9，WYS算法的总体效用更高。

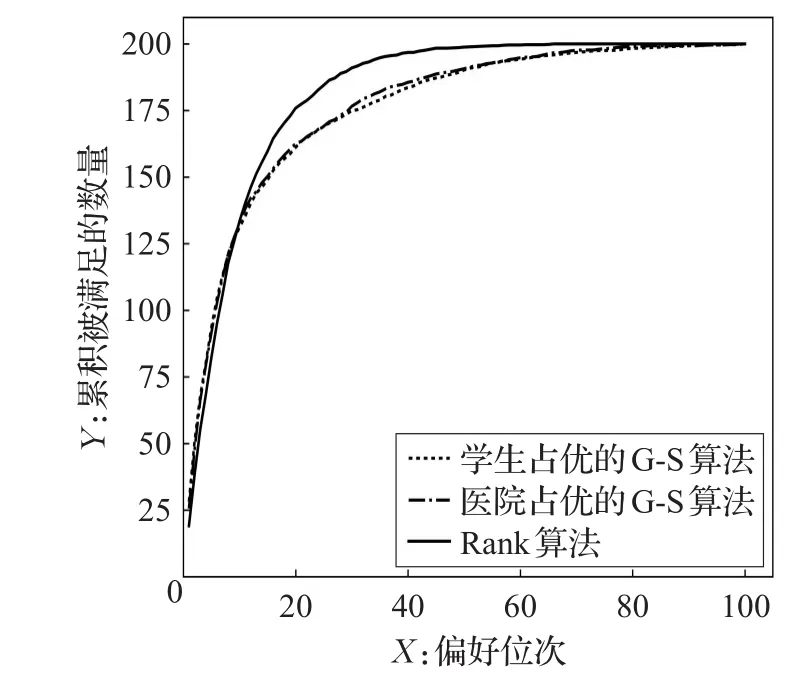
图5 10次随机实验平均的学生和医院整体偏好位次满足累积曲线

（4）目前尚未从理论上证明算法的稳定性，但大量随机偏好序的一对一、一对多实验发现随着优先级设定不同，WYS算法总能产生不同于经典G-S算法的多种稳定匹配结果，即WYS算法产生的结果不存在阻碍对。

在进行了多轮10次一组的实验之后，发现上述（1）～（4）结论在每一轮实验中都成立，另针对一对多、多对多匹配进行了实验，上述（1）～（4）结论仍成立，说明算法具有相当的稳健性。

5 结束语

本文针对传统双边匹配算法存在的问题提出了全新的WYS算法，并按照Roth的经济工程学范式设计实验对WYS算法的性质进行了深入探讨。WYS算法解决了G-S、Roth-Peranson等经典双边匹配算法的单边占优问题，扩展了双边匹配算法的适用范围，尤其有助于应对主体偏好一致性不强的场景，如婚姻匹配、银行信贷与小微企业匹配、教育招生匹配、人岗匹配等问题，为相关领域基于双边匹配理论的市场设计实践提供了更强的理论基础。WYS算法对于传统算法中效用最差的群体满意度有显著提高，对于提高主体参与意愿，维持市场厚度有重要意义。同时WYS算法通过外生指定不同优先级，能够倾向性地照顾不同主体，产生多种不同的稳定匹配，而非如传统算法只能选择照顾参与双方中的某一方，为匹配机构的宏观调控和精细干预提供了可操作空间。WYS算法可通过设定匹配容量而用于一对一、一对多和多对多双边匹配问题，具有相当的通用性。

参考文献：

[1]魏立佳.从微观理论到社会实践——市场设计的最新进展综述[J].世界经济文汇，2013，56（3）：89-104.

[2]Che Y K，Gale I L.Market versus non-market assignment of ownership，1328984[R].Rochester，NY：Social Science Research Network，2009.

[3]Roth A E.The economist as engineer：Game theory，experimentation，and computation as tools for design economics[J].Econometrica，2002，70（4）：1341-1378.

[4]Roth A E，Peranson E.The redesign of the matching market for American physicians：Some engineering aspects of economic design[J].American Economic Review，1999，89（4）：748-780.

[5]Milgrom P.Critical issues in the practice of market design[J].Economic Inquiry，2011，49（2）：311-320.

[6]Sönmez T，Ünver M U.Matching，allocation，and exchange of discrete resources[M]//Jess B，Jackson M O，Alberto B.Handbook of Social Economics.North Holland：Elsevier，2011：781-852.

[7]Budish E.Matching“versus”mechanism design[J].SIGecom Exchanges，2012，11（2）：4-15.

[8]Gale D，Shapley L S.College admissions and the stability of marriage[J].The American Mathematical Monthly，1962，69（1）：9-15.

[9]Roth A E.The economics of matching：Stability and incentives[J].Mathematics of Operations Research，1982，7（4）：617-628.

[10]Klumpp T.Two-sided matching with spatially differentiated agents[J].Journal of Mathematical Economics，2009，45（5）：376-390.

[11]Erdil A，Ergin H.Two-sided matching with indifferences[J].Journal of Economic Theory，2017，171（6）：268-292.

[12]Castillo M，Dianat A.Truncation strategies in two-sided matching markets：Theory and experiment[J].Games and Economic Behavior，2016，98（4）：180-196.

[13]Gharote M，Patil R，Lodha S，et al.Assignment of trainees to software project requirements：A stable matching based approach[J].Computers&Industrial Engineering，2015，87（9）：228-237.

[14]Byun J，Jang S.Effective destination advertising：Matching effect between advertising language and destination type[J].Tourism Management，2015，50（5）：31-40.

[15]Xu X，Wang C，Zeng Y，et al.Matching service providers and customers in two-sided dynamic markets[J].IFACPapersOnLine，2015，48（3）：2208-2213.

[16]Chen J，Song K.Two-sided matching in the loan market[J].International Journal of Industrial Organization，2013，31（2）：145-152.

[17]Silveira R，Wright R.Venture capital：A model of search and bargaining[J].Review of Economic Dynamics，2016，19（1）：232-246.

[18]Roth A E.Deferred acceptance algorithms：History，theory，practice，and open questions[J].International Journal of Game Theory，2008，36（3）：537-569.

[19]Roth A E.The evolution of the labor market for medical interns and residents：A case study in game theory[J].Journal of Political Economy，1984，92（6）：991-1016.

[20]Roth A E.What have we learned from market design?[J].The Economic Journal，2008，118（527）：285-310.

[21]Itai A，Yash K，Jacob D L.Unbalanced random matching markets：The stark effect of competition[J].Journal of Political Economy，2016，125（1）：69-98.

[22]李铭洋，樊治平，乐琦.考虑稳定匹配条件的一对多双边匹配决策方法[J].系统工程学报，2013，29（4）：454-463.

[23]Kojima F，Pathak P A，Roth A E.Matching with couples：Stability and incentives in large markets[J].The Quarterly Journal of Economics，2013，128（4）：1585-1632.