基于径向基点插值的Chan-Vese模型图像分割算法

李淑玲

LI Shuling

重庆师范大学 数学科学学院，重庆 401331

School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China

1 引言

图像分割是图像处理的基础，水平集方法作为一种有效的分割方法被广泛地应用于图像分割领域[1]。基于水平集方法，Chan和Vese提出了Chan-Vese模型，简称为CV模型[2]，这是近年来被大量研究的一种典型的区域型几何活动轮廓模型，并且成功应用于众多领域的图像分割问题。

CV模型中涉及依赖于时间的非线性偏微分方程，通常用迎风有限差分法等计算方法数值求解。这些算法虽然得到了广泛应用，但是演化速度常常较慢，计算效率低下，主要原因是：（1）算法计算量大，耗时较多；（2）演化结果严重依赖于水平集初始轮廓的形状、大小和位置，不同的初始轮廓可能导致不同甚至错误的分割结果；（3）为了保证演化过程的稳定性，需要定期使用耗时的算法来重新初始化水平集函数；（4）缺乏明确的演化终止条件，设置固定演化次数的做法不够高效。因此，如何高效地数值求解CV模型在水平集图像分割领域里十分重要。为此，很多学者对CV模型进行了改进和完善，比如文献[3-4]提出的改进CV模型解决了演化结果严重依赖于初始轮廓的缺陷，文献[5-7]提出的改进CV模型避免了重新初始化过程，文献[8-10]分别利用多重网格法、共轭梯度法和两点步长梯度法提高了CV模型的演化速率，但是这些文献中的CV模型仍然使用有限差分法离散求解，导致计算量偏大。

径向基函数被广泛应用于数值求解微分方程初边值问题[11]，具有各向同性和形式简单等特征，分为紧支径向基函数和全局径向基函数两种。由于径向基函数插值的光滑性较高，用径向基函数求解CV模型时不需要重新初始化水平集函数，并且分割结果几乎不受水平集初始轮廓的影响，因此计算速度明显快于基于有限差分格式的算法[12-14]。文献[12]用紧支径向基函数求解了CV模型。紧支径向基函数形成的插值矩阵稀疏，相应方程组的求解时间较少，但是插值精度较低，所以文献[12]中的方法演化时间仍然较长。文献[13-14]用全局径向基函数求解了CV模型。全局径向基函数插值精度较高，但形成的插值矩阵稠密，且容易病态甚至奇异，导致相应方程组的求解时间较多，因此相比文献[12]中的紧支径向基函数方法，文献[13-14]中的全局径向基函数方法的演化时间只降低了20%左右。

径向基点插值法[15]是一种融入了紧支域概念的全局径向基函数方法。为了克服文献[13-14]中插值矩阵稠密且病态的不足，同时为了进一步提高文献[12-14]中算法的演化速度，本文将借助径向基点插值法建立求解CV模型的高效数值算法。该算法保留了文献[12]中紧支径向基函数方法和文献[13-14]中全局径向基函数方法的优点，既具有明确的演化终止条件，又具有较高的插值精度和演化速度，因此对水平集初始轮廓不敏感，无需重新初始化水平集函数。另外，由于径向基点插值法是一种无网格方法，所以本文算法只需要节点，不需要网格单元。实验表明，本文算法大幅度降低了文献[12-14]中算法的演化分割时间。

2 图像分割Chan-Vese（CV）模型

图像分割的CV模型可表示为[1-2，5-6]：

其中x是图像区域Ω中的空间变量，t是时间变量，φ(x,t)是水平集函数，φ0(x)表示水平集初始轮廓，V(x,φ(x,t))是如下速度函数：

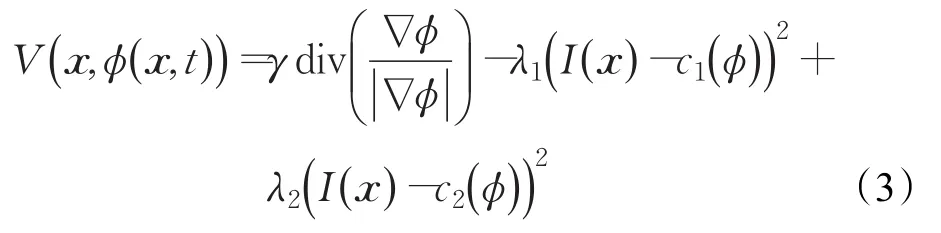
式（3）中，γ≥0、λ1＞0和 λ2＞0都是权重系数，I()x表示图像灰度。

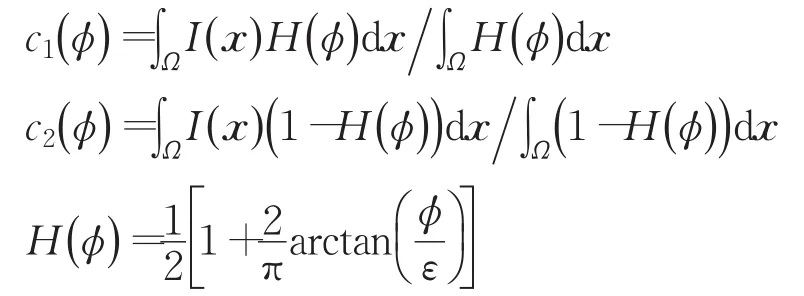
其中ε是参数。

因为径向基点插值法生成的近似函数是全局光滑的，所以令[12-14]γ=0，λ1=λ2=1，从而

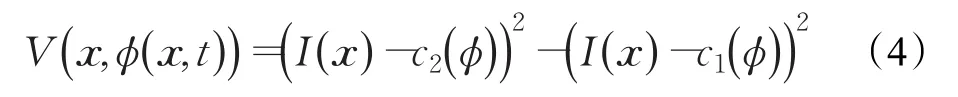
3 径向基点插值法

文献[12]和文献[13-14]分别用紧支径向基函数和全局径向基函数逼近水平集函数，但这两种径向基函数固有的缺点致使分割演化速度较慢，为此本文采用径向基点插值法逼近水平集函数。

将Ω用N个节点xj(j=1,2,…,N)离散。对任意x∈Ω，点x的影响域定义为：

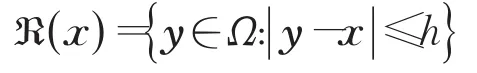
其中h是影响域ℜ(x)的半径。用表示ℜ()x内的节点的编号。

函数φ(x,t)在ℜ(x)上的径向基点插值为[15]：

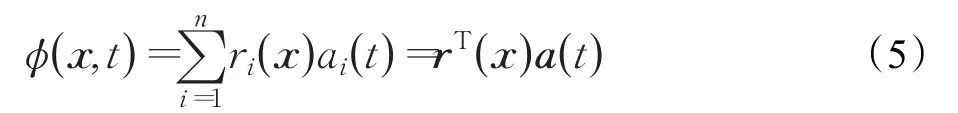
其中ai(t)是仅依赖于时间t的未知量，ri(x)是径向基函数，rT(x)=[r1(x),r2(x),…,rn(x)]，a(t)=[a1(t),a2(t),…,an(t)]T。令式（5）在ℜ(x)内的所有节点xsj处满足，可得：

即

其中。由于R对称，所以当径向基函数严格正定时，R可逆，此时方程组（6）有唯一解。本文选取，其中β是正常数。

由式（6）解出未知向量a(t) ，再代入式（5）可得：

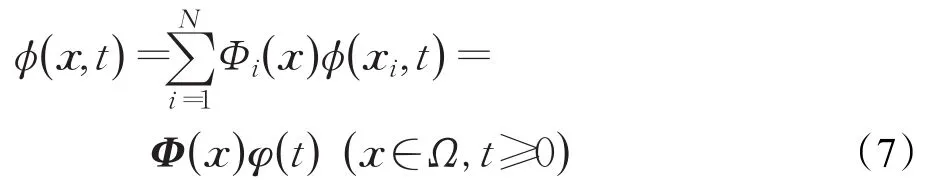
其中

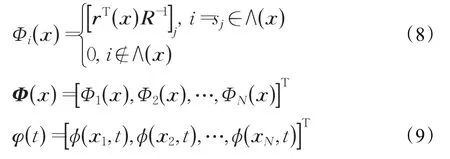
4 图像分割模型的数值解法

在传统水平集方法中，常常利用有限差分法和重新初始化算法求解式（1）和式（2）组成的偏微分方程初值问题，具有较高复杂度和较大计算量。文献[12-14]中的径向基函数图像分割算法虽然克服了传统水平集方法中的一些缺点，但算法计算量还可进一步降低。本文通过用径向基点插值法逼近水平集函数，将式（1）和式（2）转化为常微分方程组初值问题，然后设计具有终止条件的Euler法求解。

把式（7）代入式（1）可得：

令上式在所有N个节点xj成立，可得：

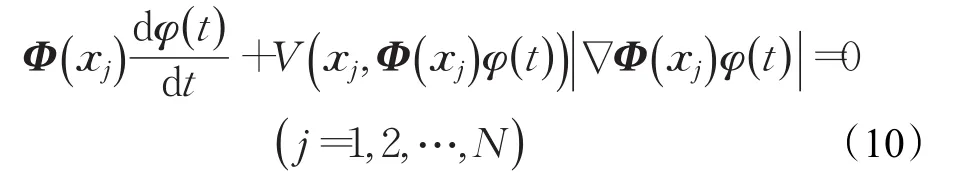
类似于文献[13-14]中的算法，为了克服水平集函数的驻点延缓演化速度的不足，可将式（10）中的替换为其规范化形式则式（10）变成：

因为形函数 Φi(x)具有Delta性质[15]，即 Φi(xj)=，所以由式（11）可得：

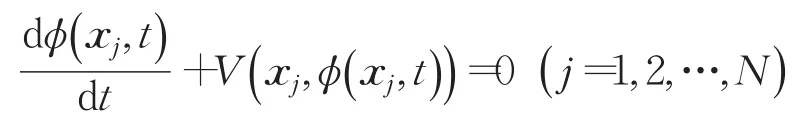
即

其中φ(t)是由式（9）给出的未知向量。

用向前Euler法离散式（12）可得：

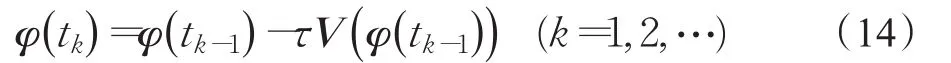
其中tk=tk-1+τ，t0=0，τ＞0是时间步长。根据式（2），计算式（14）的初始条件为：

图像分割的主要任务是找出目标图像的轮廓曲线。由于φ(x,t)与任一非零实数的乘积不改变φ(x,t)=0的x值（即轮廓曲线的位置），因此为了给出明确的演化终止条件，可在每次计算式（14）之后将φ(tk)规范化，即令，此时可设置演化终止条件为[12-14]：

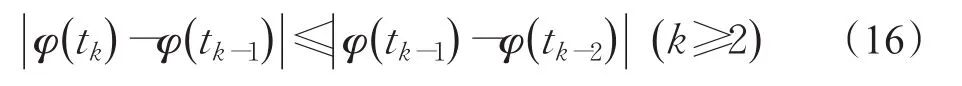
迭代计算式（14）终止之后得到φ(tk) ，此即为式（9）中向量φ(t)的近似值，然后可由式（7）计算区域Ω内任一点x处的水平集函数φ(x,t)，最后由φ(x ,t)=0确定目标图像的轮廓曲线。

因此，本文图像分割算法的主要步骤如下：

（1）输入需要分割的图像，选取参数ε和β、时间步长τ，令t0=0，k=1。

（2）将图像区域用节点 x1，x2，…，xN离散，由式（8）计算Φi(x) ，i=1,2,…,N 。

（3）初始化水平集函数得φ0(x)i，i=1,2,…,N ，再由式（15）得

（4）令tk=tk-1+τ，由式（4）计算i=1,2,…,N ，再由式（13）得

（5）由式（14）计算φ(tk)，令

（6）检验式（16），如果不成立则令k=k+1并返回步骤（4），否则停止迭代并转向步骤（7）。

（7）由式（7）计算图像区域内的水平集函数，确定目标图像的轮廓曲线，输出分割结果。

因为用径向基点插值法生成的近似函数是全局光滑的[15]，所以类似于文献[12-14]中的算法，本文算法能避免重新初始化过程和克服轮廓初始化问题。其次，由于建立了明确的演化终止条件，本文算法不需要事先设置演化次数。再次，由于使用径向基点插值法，本文算法比文献[12-14]中的算法演化速度更快。

5 实验结果

使用本文算法、文献[2]的有限差分算法、文献[12]的紧支径向基函数算法以及文献[13-14]的全局径向基函数算法分割一些图像，比较计算时间和分割精确性。实验参数选取如下：对本文和文献[12-14]的算法，ε=1，β=8，τ=1；对文献[2]的算法，ν=0，μ=0.5×2552，λ1=λ2=1，τ=0.1，每迭代10次对水平集函数重新初始化1次，迭代最大次数为5 000。实验软件为Matlab7.0.1，硬件环境为Intel®Core™ i7-6500U CPU@2.50 GHz，8.00 GB内存。

表1给出了在不同初始轮廓曲线时分割表1（a3）中图像的结果。对于本文和文献[12-14]的算法，不管初始轮廓曲线在何处（表1（a1，a2）），甚至缺乏初始轮廓（表1（a3））时，这四种算法都能正确分割。对于文献[2]的算法，当目标被初始轮廓包围时才能分割正确（表1（f1）），否则分割错误（表1（f2，f3））。

表2给出了表1中分割需要的计算时间。文献[12-14]中算法所需时间约为本文算法的25～35倍，而文献[2]中算法所需时间更多，所以本文算法所需时间非常小，具有很高的演化速度。

表1 五种算法在不同初始轮廓时的分割结果

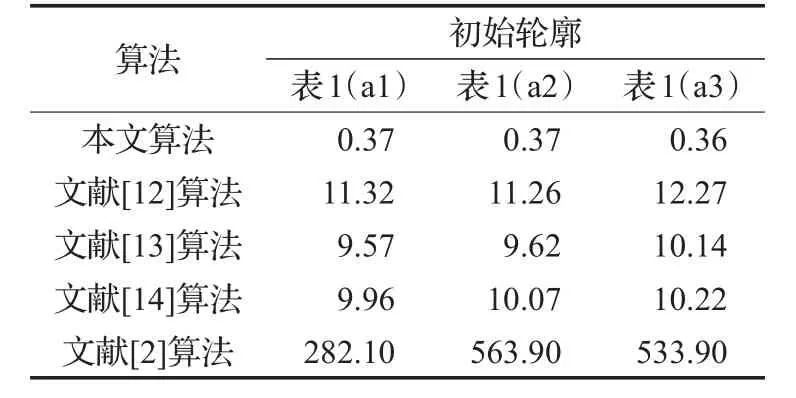
表2 表1中分割的计算时间 s

表3给出了表1中分割的Dice相似性系数(DSC)和错误分割率(RSE)[13]。DSC越接近1，同时RSE越接近0，分割精度越高。表3中的数据表明本文算法和文献[12-14]中算法都具有较高的分割精度，而文献[2]中算法的精度要差一些。

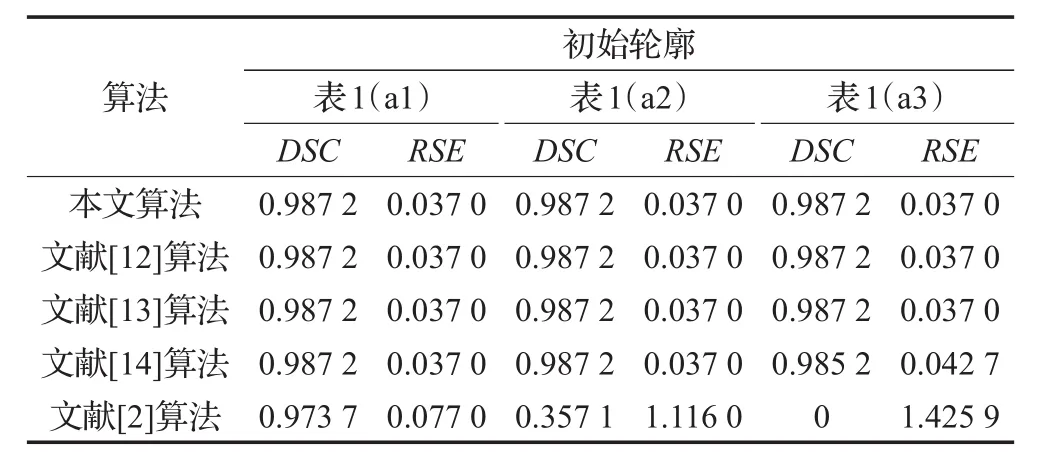
表3 表1中分割的DSC和RSE

表4给出了在没有初始轮廓时本文算法和文献[2，12-14]中算法分割表4（a1）～（a5）中图像的结果。本文和文献[12-14]的算法都能正确分割，但文献[2]的算法无法正确分割。表5给出了表4中分割需要的计算时间，本文算法所需时间比文献[12-14]中的算法少很多。

表4 五种算法对不同图像在没有初始轮廓时的分割结果

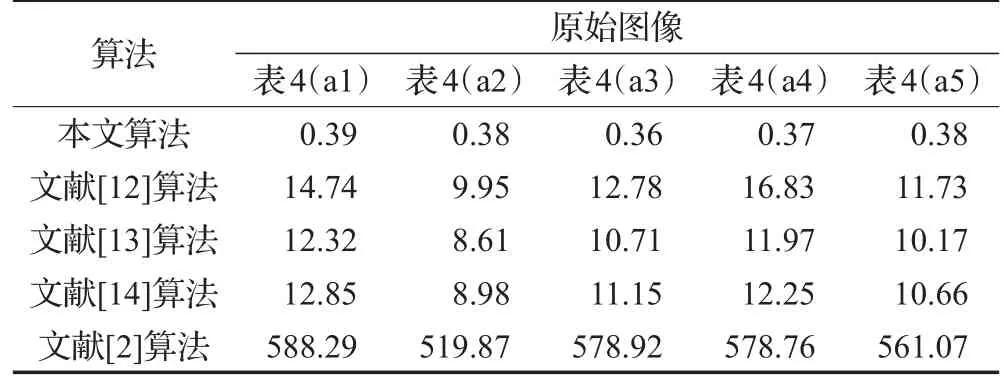
表5 表4中分割的计算时间s

表6第一行给出了5幅真实图像，表6第二行和第三行表明本文算法和文献[14]的算法在没有初始轮廓时都能正确地分割这些图像。在实验中发现文献[12]和文献[13]的算法也能正确分割这5幅真实图像，但本文算法所需时间比文献[12-14]中的算法少很多。

6 结束语

针对水平集CV模型演化耗时的缺点，本文提出了一种高效数值求解CV模型的图像分割算法。该算法通过利用径向基点插值法逼近水平集函数，将CV模型转化为常微分方程组初值问题，然后用具有迭代终止条件的向前Euler方法求解。相比基于有限差分格式的算法，本文算法无需复杂费时的重新初始化过程，对水平集初始轮廓不敏感，也不需要事先设置演化次数，从而降低了算法的复杂度和计算量，实验表明本文算法分割效果更好，并且演化速度快很多。相比基于紧支径向基函数和全局径向基函数的算法，实验表明分割效果几乎相同，但本文算法计算时间明显少很多，演化速度快了25～35倍。

表6 本文算法和文献[14]的算法对5幅真实图像在没有初始轮廓时的分割结果

参考文献：

[1]Tsai R，Osher S.Level set methods and their applications in image science[J].Comm Math Sci，2003，1：623-656.

[2]Chan T，Vese L.Active contours without edges[J].IEEE Trans on Image Process，2001，10：266-277.

[3]顾鹏程，黄福珍.基于改进Chan-Vese模型的电力设备红外图像分割[J].计算机工程与应用，2017，53（10）：193-196.

[4]Abdelsamea M M，Gnecco G，Gaber M M.A SOM-based Chan-Vese model for unsupervised image segmentation[J].Soft Comput，2017，21：2047-2067.

[5]Li C，Xu C，Gui C，et al.Distance regularized level set evolution and its application to image segmentation[J].IEEE Trans on Image Process，2010，19：3243-3254.

[6]Zhang K H，Zhang L，Song H H，et al.Re-initialization free level set evolution via reaction diffusion[J].IEEE Trans on Image Process，2013，22：258-271.

[7]张雯，王小鹏，李志强，等.分水岭优化的C-V模型脑肿瘤图像分割[J].计算机工程与应用，2017，53（5）：176-180.

[8]Badshah N，Chen K.Multigrid method for the Chan-Vese model in variational segmentation[J].Commun Comput Phys，2008，4：294-316.

[9]屈健健，应时辉，彭亚新.Chan-Vese模型的共辄梯度算法[J].应用数学和计算数学学报，2013，27（4）：469-477.

[10]彭亚新，陈飒飒，沈超敏，等.求解图像分割CV模型的BB算法[J].运筹学学报，2014，18（3）：79-87.

[11]陈文，傅卓佳，魏星.科学与工程计算中的径向基函数方法[M].北京：科学出版社，2014.

[12]Gelas A，Bernard O，Friboulet D，et al.Compactly supported radial basis functions based collocation method for level-set evolution[J].IEEE Trans on Image Process，2007，16：1873-1887.

[13]李淑玲，李小林.全局正定径向基函数在图像分割中的应用[J].计算机工程与应用，2014，50（6）：139-143.

[14]Li S L，Li X L.Radial basis functions and level set method for image segmentation using partial differential equation[J].Appl Math Comput，2016，286：29-40.

[15]Liu G R.Mesh-free methods：Moving beyond the finite element method[M].Boca Raton：CRC Press，2009.