线性规划中关于避免人工变量的一个注记

刘雁灵，李 菲

（1.长治医学院 数学教研室；2.长治医学院 卫生信息与管理系，山西 长治 046000）

在线性规划模型中，若约束条件出现“≥”或者“=”的情况，常见的方法是引入人工变量构造人工基再使用大M法或两阶段法来求解，但引入人工变量使得变量增多，线性规划问题显得更加复杂.大量文献讨论了避免引入人工变量的方法，文献[1]通过对增广矩阵实施初等行变换来寻找m个列线性无关的向量组，若右项非负则使用单纯形法计算，否则重新寻找m个列线性无关的向量组，该法计算量过大；文献[2]对文献[1]的方法进行了改进，在系数矩阵中只选择m个列线性无关的向量组B，对矩阵(B,b)作初等行变换，若右项非负再把增广矩阵其他元素考虑进去作同样的行变换，但计算量仍大；文献[3]是通过对单纯形表做旋转变换来计算的；文献[4]通过对增广矩阵实施初等行变换使得系数矩阵产生单位矩阵，但这一过程要求右项必须保持非负，这就对行变换的过程增加难度，有时亦很难达到；文献[5]在对增广矩阵作初等行变换时并不要求右项非负，在求解过程中再根据右项和检验数行元素的正负情况使用单纯形法或者对偶单纯形法来计算.本文在前面文献的基础上，给出了新的改进方法，一方面在迭代过程中不要求右项的非负性，另一方面也推广了单纯形法中比值θ的计算方法，并通过实例加以验证.

1 避免人工变量的新算法

本文中的检验数采用σj=zj-cj[6]的计算方法，这样原问题和其对偶问题解的可行性看得更直观.

本文方法的思路为：对增广矩阵实施初等行变换寻找一个初始基，对其单纯形表（此时检验数行和右项均可有负）用单纯形法或对偶单纯形法进行换基迭代，经过有限次迭代最终求得最优解（若最优解存在）.

算法步骤如下：

（1）将线性规划问题标准化，对增广矩阵作初等行变换，使得系数矩阵的位置产生m阶单位矩阵（进行列交换之后得到的），这里不要求右项非负；

（2）列出初始单纯形表；

（3）若存在负的检验数，则采用单纯形法：用负数绝对值大的那列作为主列，用主列元素去除右项（主列元素与对应的右项同号时），即负元素对应行右项为负时，正元素对应行右项为正时，才可除，产生比值θ，选择θ最小的基变量为换出变量，实施换基迭代；

（4）若不存在负的检验数，但是右项有负值，则用对偶单纯形法进行换基迭代；

（5）若存在负检验数时，主列元素没有和右项同号的，则不能产生比值θ，故找不出换出变量，说明该线性规划问题无最优解.

注：步骤（3）（4）（5）不分先后，要根据不同的情况选择步骤.

2 举例

例1 求解线性规划问题[2]

解 将约束条件化为等式得

写出增广矩阵并作初等行变换，任意寻找一个单位矩阵

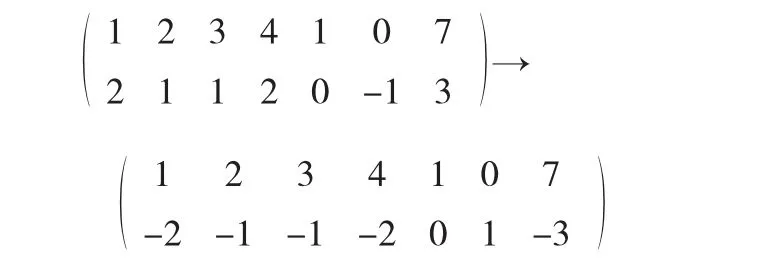
于是得到一个不可行基(P5,P6)，列出初始单纯形表

x1 x2 x3 x4 x5 x6 b θ-5 2 -3 6 0 0 x5 0 1 2 3 4 1 0 7 7/4 x6 0 -2 -1 -1 -2 0 1 -3 3/2→σj 5 -2 3 -6↑ 0 0

主列是x4列，用4除7得比值7/4，用-2除-3得比值3/2，选择比值小的3/2对应的x6换出，经过行变换（轴心项为a24=-2），得单纯形表

x1 x2 x3 x4 x5 x6 b θ-5 2 -3 6 0 0 x5 0 -3 0 1 0 1 2 1 1/2→x4 6 1 1/2 1/2 1 0 -1/2 3/2 σj 11 1 6 0 0 -3↑

主列是x6列，用2除1得比值1/2，-1/2对应的右项是正值3/2，不能求比值，故选择x5换出，经过行变换（轴心项为a16=2），得单纯形表

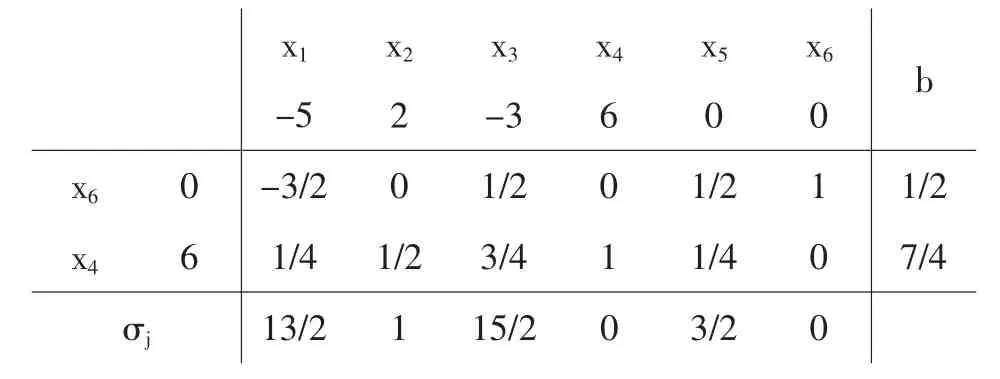
x1 x2 x3 x4 x5 x6 b-5 2 -3 6 0 0 x6 0 -3/2 0 1/2 0 1/2 1 1/2 x4 6 1/4 1/2 3/4 1 1/4 0 7/4 σj 13/2 1 15/2 0 3/2 0

检验数行和右项都非负，此表已是最终形表，最优解为：

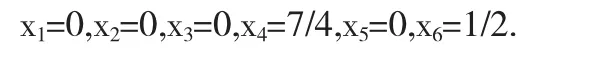
例2 求解线性规划问题[4]

解 本模型已是标准型，写出增广矩阵并作初等行变换，任意寻找一个单位矩阵

于是得到一个不可行基(P4,P5,P3)，列出初始单纯形表

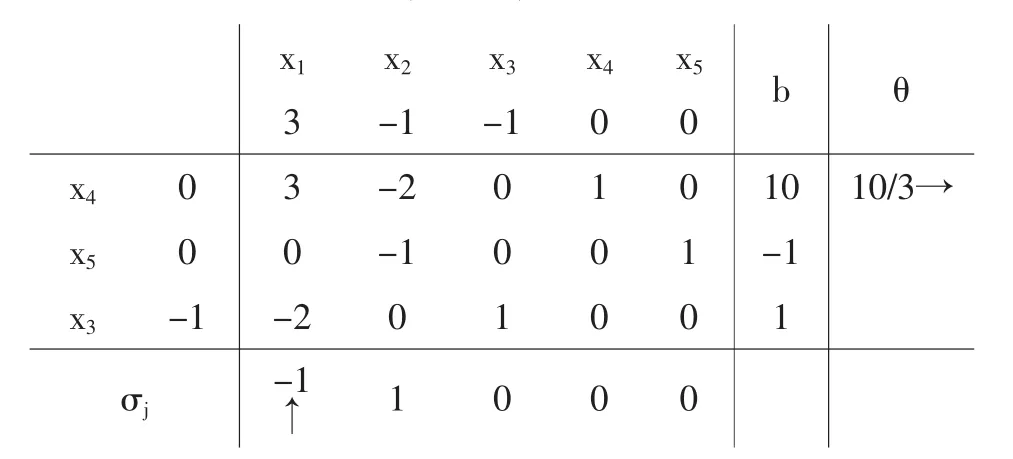
x 1 x 2 x 3 x 4 x 5 b θ 3 -1 -1 0 0 x 4 0 3 -2 0 1 0 1 0 1 0/3→x 5 0 0 -1 0 0 1 -1 x 3 -1 -2 0 1 0 0 1 σ j-1↑ 1 0 0 0

主列为x1列，用3除10得比值10/3，0不能除-1，-2对应的右项是正值1，不能求比值，故选择x4换出，经过行变换（轴心项为a11=3），得单纯形表

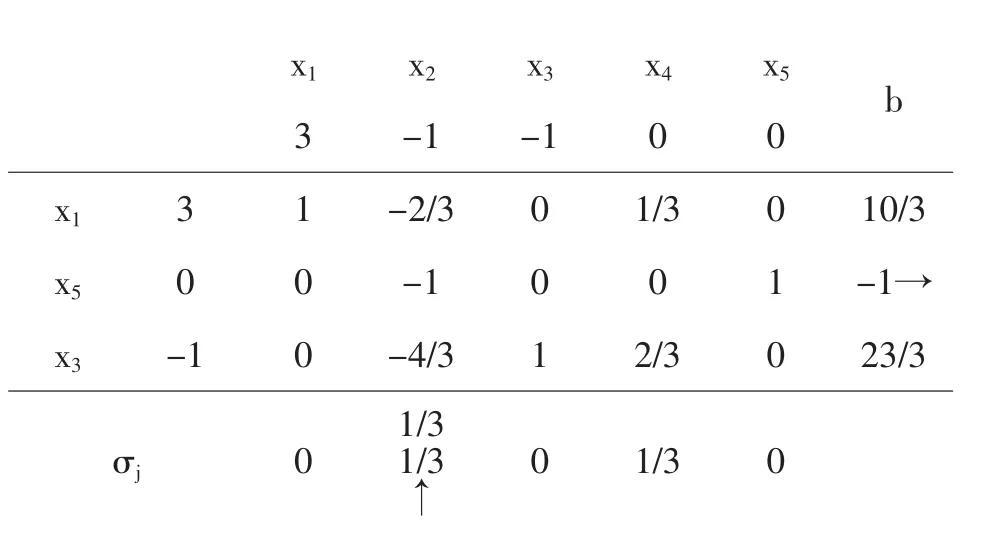
x1 x2 x3 x4 x5 b 3 -1 -1 0 0 x1 3 1 -2/3 0 1/3 0 10/3 x5 0 0 -1 0 0 1 -1→x3 -1 0 -4/3 1 2/3 0 23/3 σj 0 1/3 1/3↑ 0 1/3 0

此时检验数行元素全是非负的，但右项有负值-1，故利用对偶单纯形法求解，选x5换出，用该行负值-1除相应的检验数1/3再取绝对值得比值1/3，故选x2换入，经过行变换（轴心项为a22=-1），得单纯形表

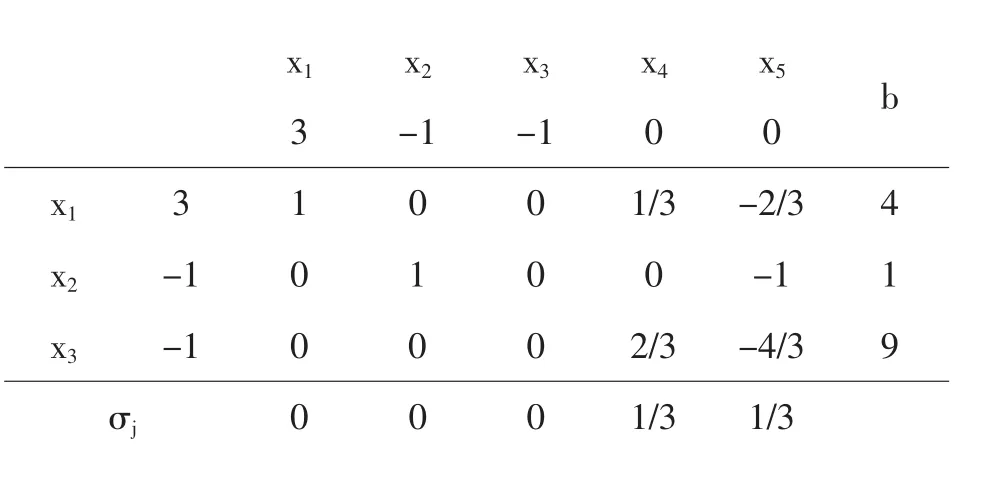
x1 x2 x3 x4 x5 b 3 -1 -1 0 0 x1 3 1 0 0 1/3 -2/3 4 x2 -1 0 1 0 0 -1 1 x3 -1 0 0 0 2/3 -4/3 9 σj 0 0 0 1/3 1/3

此表已是最终形表，最优解为：

3 结束语

在文献[1]-[5]的基础上，本文给出了一种避免人工变量的新算法：首先对增广矩阵实施初等行变换之后得到的右项可以有负，其次在迭代过程中将单纯形法计算θ的过程加以推广，主列不仅只有正的元素可以除正的右项，负的也可以除负的，而且同样可以得出正确的结果（最优解存在的情况下），若最优解不存在，亦可判断出.通过几个实例的计算，可以看出该法的可行性，与大M法和两阶段法相比，计算量得到减少.

〔1〕 吴振奎.线性规划中一个避免人工变元的方法[J].运筹与管理，1998（2）：78-82.

〔2〕 王志江.线性规划中人工变量的作用不应忽视[J].运筹与管理，1999（3）：93-96.

〔3〕 吴延东.求线性规划问题可行基的一种方法[J].运筹与管理，1999（1）：41-45.

〔4〕 吕林霞，茹少峰，申卯兴.线性规划中模型的单纯形法初始可行基选择研究[J].西北大学学报（自然科学版），2011（4）：589-592.

〔5〕 周学松，赵恒.线性规划中一个避免人工变元的方法的改进[J].运筹与管理，2011（5）：31-38.

〔6〕 宁宣熙.运筹学实用教程[M].北京：科学出版社，2013.