基于米字型结构元的形态学边缘检测算法研究
陈 亮
(武夷学院 数学与计算机学院,福建 武夷山 354300)
伴随着计算机技术的快速发展,数字图像处理技术开始诞生,在医药、航空、军事、工程、电子商务中得到广泛应用.
对图像来说边缘是其最基本的属性,边缘包含如此众多重要的信息.有效地检测图像边缘,对后续的图像处理至关重要的作用,但是,现实生活中存在着噪音,传统的边缘检测算法对于含有噪声的图像往往效果不佳.为了去除噪声的影响,学者们基于形态学知识,提出了多尺度多方向的结构元的形态学边缘检测算法[1],有效地抑制住了噪音影响,后续学者们又提取不同的形态学改进算法.在此基础之上,本文首次提出米字型结构元的改进形态学边缘提取算法,米字型结构元在保证各方向的信息的基础上,在结构元扩大的过程中有效地减少了运算量.再结合均值的思想的改进形态学边缘提取方法,在对含噪声的图像有效的提取边缘的基础上,又能提高运算效率.
1 数学形态学
1.1 基本原理[2]
形态学是建立在严格数学理论上的一门新兴学科,是一种新型的数字图像处理方法和理论.数学形态学运算主要用于二值图像的处理,可将其引申到灰度图像领域,形态学主要包括腐蚀、膨胀、开运算、闭运算等.
1.1.1 腐蚀
f是一副图像,结构元素b对f的灰度腐蚀记为:fΘb,其定义为

其中,Db为b的定义域.
为了说明腐蚀的原理,通过例子来解释:

其中X为被处理的图像(1表示黑色),B为结构元素;其中为1的部分是中心点,既是当前所需要处理的位置;腐蚀的方式是:用B的中心点和X上的点一个一个地对比,若B上的所有点都在X的范围内则该点保留,否则将该点去掉;右边是腐蚀后的结果.由此可以发现,它仍然在原来X的范围内,且比X包含的点要少,就像X被腐蚀掉了一层.
1.1.2 膨胀
设f是一副图像,结构元素b对f的灰度膨胀记为:f⊕b,定义为
(f⊕b)(x,y)=max{f(x-x',y-y')+b(x',y')|(x'+y')∈Db}
其中,Db为b的定义域.为了说明膨胀的原理,通过以下例子来解释:

其中X为被处理的图像(1表示黑色),B为结构元素;其中为1的部分是中心点,既是当前所需要处理的位置;膨胀的方式是,用B的中心点和X上的点及X周围的点一个一个地对,如若B上有一个点落在X的范围内.则该点就为黑;右边是膨胀后的结果.由此也可以发现,它包括X的所有范围,就像X被膨胀了一圈.
1.1.3 开、闭运算
结构元素b对图像f的开运算为:

则开运算是先腐蚀再膨胀的运算,即open(X).如:

从结果可以得出,原图经过开运算后,某些孤立的小点被消掉了.
则b对图像f的闭运算为:

则闭运算是先进行膨胀后进行腐蚀的一种运算,即 close(X).如:

从结果可以得出,原图经过闭运算后,弥合了断裂的地方.
数学形态学是图像处理强有力的工具,它们的组合构建出新的梯度算子进行边缘提取,可以较好保留图像的细节特征的同时又可以防止噪声.
1.2 形态学边缘提取算法
假设给定图像为f和结构元se,则利用形态学的膨胀和腐蚀运算进行边缘b(f)提取方法如下:
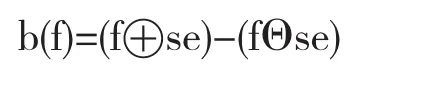

图1-1 传统的形态学边缘检测算法分别对原图和含噪声图像进行边缘检测
如上图传统的边缘提取对于没有噪声的图像提取效果较好,但是对与含噪声图像就失去的效果.在此基础之上,学者们针对有噪声的图像提出多尺度、多结构元的边缘检测,并取得较好的效果.
2 基于米字型结构元改进形态学边缘提取算法
形态学中可以通过多次的开闭运算,来对图像进行边缘提取,能够有效地防止噪声的干扰.然而传统的开闭运算用到的是固定的结构元进行运算,在边缘提取的准确性和时效性还有提高的空间.通过对上述问题的研究,本文利用不同尺度的米字型窗口的结构,在进行形态学边缘提取的基础之上再利用小尺度结构元进行腐蚀运算,有效减少小细节的干扰,最后结合均值的思想,以不同尺度的米字型窗口的结构元进行运算后再取均值运算,得到最后图像边缘的有效信息.
2.1 基本原理


其中 f为原图,B1、B2、B3、B4分别为 3*3、5*5、7*7的米字型结构元.
2.2 算法流程图

图2-1 改进形态学边缘检测算法流程图
3 仿真实验及结果分析
本文所改进的算法中用方形结构元和米字型结构与其他已存在的两种形态学边缘检测算法分别对没有噪声下、含10%的椒盐噪声下、含20%的高斯噪声的图像进行仿真实验,效果图如下
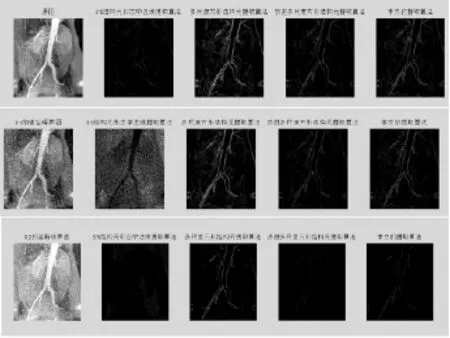
图3-1 四种形态学边缘检测算法分别对原图和含噪声图像进行边缘检测
从上述实验图可以看出,当没有噪声时几种算法效果都不错,但是本文的算法在检测主要边缘,同时消去其他细小的部分,检测效果更加准确.对于有噪声的图像,传统的形态学边缘检测效果不佳,其他三种算法都检测出了主要边缘,跟无噪声的情况一致,本文的算法都在检测主要边缘,同时消去其他细小的部分,检测效果更加准确.这体现出了本文的算法的优越性.

表1 不同噪声浓度下不同算法的滤波信噪比
从上表可以看出传统5*5固定结构元的形态学边缘检测算法用时最高,多尺度方形结构元的形态学边缘检测算法用时做少,改进多尺度方形结构元的形态学边缘检测算法用时稍微多一些,而本文的检测算法用时相对较少,体现出米字型结构元减少运算量的作用.本文算法虽然用时稍高于多尺度方形结构元的形态学边缘检测算法,但是本文检测算法在检测的准确上高,所以体现本文检测算法的优越性.
〔1〕 吴朔媚,韩明,王敬涛.基于多尺度多方向结构元素的形态学图像边缘检测算法[J].量子电子学报,2017,34(03):278-285.
〔2〕 Gonzalez,R.C.等著,阮秋琦等译.数字图像处理[M].第二版,北京:电子工业出版社,2007.255-284.
〔3〕 唐晓强.自适应形态学图像边缘检测算法的研究[D].乌鲁木齐:新疆大学,2010.
〔4〕 蔡正涛.基于双结构元的数学形态学边缘检测方法[D].西安:西北工业大学,2003.
〔5〕 贺萌.基于自适应形态学的边缘检测及应用[D].长沙:中南大学,2013.

