期刊被引量的分布及影响因子的失真——以7种物理学综合期刊为例

■严建新

1)广西大学马克思主义学院,广西南宁市西乡塘区大学东路100号 5300042)大连理工大学科学学与科技管理研究所暨WISE实验室,辽宁省大连市甘井子区凌工路2号 116024

目前，初创于1972年的期刊影响因子(Journal Impact Factor，JIF)在许多国家的科研管理中仍是评价期刊、学者和科研机构的重要指标之一[1-3]，我国许多科研机构也将成果发表期刊的影响因子作为分配科研经费、晋升职称和发放奖金的主要依据之一。不少学者分析了影响因子在时间窗口、数据采集、计算等方面存在的不足[4]，但期刊被引量的偏态分布对影响因子评价功能所产生的影响仍有待深入探讨。

国内外一些学者对计量指标分布问题的探索颇具启发性。毛国敏等[5]分学科领域研究中国学术期刊的载文量、总被引量和影响因子在期刊间的分布，发现这些指标呈不均匀分布；俞立平等[6]研究发现，影响因子、被引半衰期、特征因子等7项指标在期刊间均为右偏分布，并认为指标的平均值难以代表各期刊在该指标上的平均水平；Weale等[7]和Metze[8]指出，以影响因子评价期刊的前提是被引量在载文间呈正态分布，样本呈正态分布时平均值才有意义；Bornmann等[9]在探讨科研评价问题时提出，期刊被引量在载文间呈较高偏离程度的偏态分布时，期刊影响因子是失真的，但未提及具体细节及如何修正影响因子的失真。本研究以2011—2015年度7种物理学综合期刊为样本，分析期刊被引量在载文间的分布特征及不均匀程度，在此基础上提出修正影响因子失真的方法。

1 研究思路与方法

1.1 研究思路

影响因子是为表征并横向比较期刊影响力而设计的指标。原则上，各期刊被引量与载文间应呈均匀分布或正态分布。当分布条件不能充分满足时，影响因子将会出现失真。洛伦兹曲线和反映分布不均匀程度的基尼系数G已被广泛应用于各种指标分布差异的研究。既然引用的不均匀分布能导致影响因子失真，可根据分布的均匀程度(1-G)对影响因子失真进行修正。

1.2 数据获取

根据科睿唯安SCI-E数据库的期刊分类和2015年度《期刊引证报告》(JournalCitationReport，JCR)，笔者选择物理学综合类中影响因子不同的7种期刊(表1)，按与影响因子相对应的时间窗口，逐年、逐篇从数据库中提取各期刊学术载文的被引频次。学术载文包括研究论文、综述论文和会议论文。影响因子的计算还涉及少量其他类型文献的被引频次，但本研究仅探讨此3类文献的被引量在这些文献间的分布。为行文方便，笔者将期刊的这3类文献在某一年度的被引频次之和简称为总被引量。

表1 2011—2015年7种物理学期刊的影响因子、载文被引频次的标准差和引用分布曲线的偏度

1.3 数据处理与计算

以2015年度NatPhys为例。2013—2014年，NatPhys的载文量为253篇，其2015年总被引频次为4616次。将各载文按被引频次由低到高排序后进行被引频次和篇数累积计算：

(1)

图1 2015年度Nat Phys的洛伦兹曲线

式中xi和yi分别为载文数量和总被引频次的累积坐标值，xiN为累积到第i篇载文的篇数，yiC为累积到第i篇载文的被引频次。以坐标值xi和yi绘制出总被引量在载文间分布的洛伦兹曲线L(图1)。L将正方形对角线下方的三角形分为A和B两个区域，基尼系数G为A的面积SA与三角形面积SΔ的比值。因SΔ=1/2，SA=SΔ-SB，SB近似等于各小梯形面积之和，因此基尼系数G为

(2)

2 结果与讨论

2.1 期刊影响因子及其默认前提

期刊的影响力以其载文影响力为基础。在纸刊时代，学者主要根据期刊影响力来有选择地阅读期刊并引用其文献；而在网络时代，学者则主要通过主题或关键词检索文献，并且有选择地阅读和引用检索到的但刊载于不同期刊的文献。与纸刊时代相比，网络时代的引用与期刊影响力之间的关联已有所弱化，因此，对期刊全部载文的影响力进行整体评价更能客观反映该期刊的影响力。

接Garfield[1]的定义，某期刊在t年度的影响因子为IJIF(t)=C/D，其中D为该刊t-2年和t-1年的载文篇数，C为该刊在t年的总被引频次。总体而言，影响因子以载文篇均被引频次来表征期刊影响力。被引量在载文间均匀分布或呈正态分布是其隐含的默认前提，即严格意义上，只有当各期刊的被引量在载文间均为均匀分布时，以载文被引频次表征的期刊影响力才具有真实性和可比性，即使以篇均被引频次表征期刊影响力，被引量在载文间也应呈正态分布。如果被引量既非均匀分布也非正态分布，篇均被引频次就难以如实表征期刊的影响力。

通常情况下，学者主要根据相关性和重要性引用他人文献。假设期刊M和N在t-2年和t-1年的载文各为100篇，且两刊在t年总被引频次各为100次，但M刊的被引量在载文间均匀分布，而N刊的100次被引仅集中于1篇载文。在影响因子的计算窗口内，M刊的全部载文在t年都各被引用1次意味着其载文均有引用价值，而N刊仅有1篇载文被引用则意味着另外99篇没有引用价值。按影响因子定义，期刊M和N的影响因子均为1，两者影响力相同；而从载文整体影响力评价，则M刊影响力高于N刊。这一虚拟例子表明，引用分布的均匀程度是期刊评价中不可忽略的因素，期刊被引量的非均匀分布将导致以影响因子表征的期刊影响力出现不同程度的失真，被引量分布越不均匀，失真就越严重。

2.2 总被引频次分布

据2011—2015年度上述7种期刊各载文的被引频次，可绘制出期刊载文总被引频次的分布曲线(图2)。笔者发现，7种期刊中，影响因子较高的RevModPhys和NatPhys均存在由少量高被引载文构成的“长尾”，影响因子较低的4种期刊则均存在由许多低被引载文构成的“高头”，而影响因子居中等水平的PhysRevLett则既有“高头”又有“长尾”。图2所示为2015年度这7种期刊总被引频次的分布曲线，其中纵向细线为相应期刊的影响因子，细斜线为分布曲线的“头顶—末尾”连线，用以标示曲线的头尾位置。

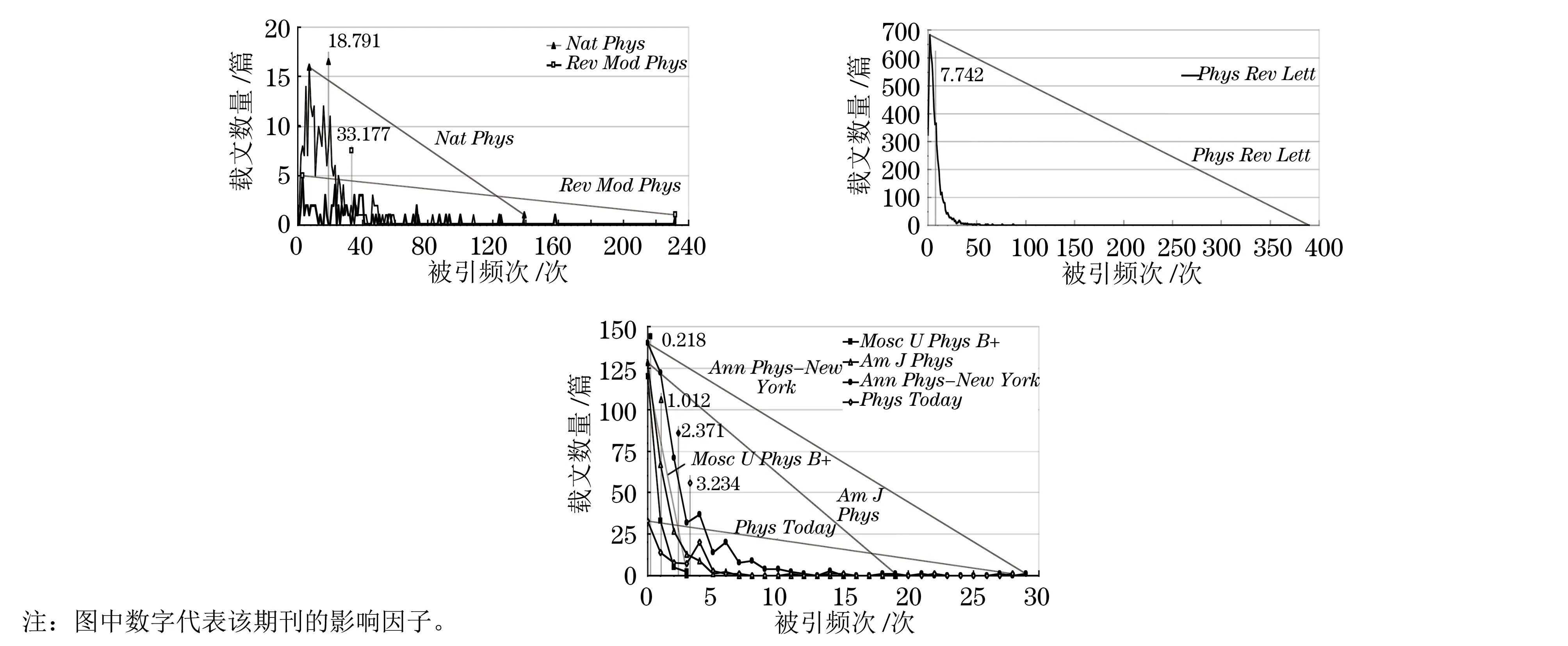
图2 2015年度7种物理学期刊总被引量分布

根据统计原理，当偏度为0时，数据呈正态分布，偏度大于0和小于0时分别为右偏和左偏分布；标准差越大，数据的离散程度越大，平均值的代表性越低。从2011—2015年度这7种物理学期刊的影响因子、载文被引频次的标准差和引用分布曲线的偏度(表1)可发现，这些分布曲线的偏度均为正值，共同特征为右偏分布，且曲线偏度与影响因子大小无关。此外，影响因子较高,期刊标准差也较大;而影响因子较低,期刊标准差相对较小。这表明，影响因子较高的期刊，载文篇均被引频次并不具有充分代表性。

2.3 分布的不均匀程度

当基尼系数G为0.3～0.4时，分布相对合理；0.4～0.5为差距较大；0.5以上则为差距悬殊，0.4被视为差距较大的警戒线。2011—2015年度，上述7种物理期刊影响因子IJIF、基尼系数G及修正后的影响因子IJIFG见表2，其中的G反映被引量分布的不均匀程度。期刊总被引量在载文间分布的另一个特征是G均高于警戒线0.4，分布差距较大甚至差距悬殊。

图3～7为2011—2015年度各期刊的总被引频次在载文间分布的洛伦兹曲线。影响因子计算窗口内，如有若干载文未被引用，则其被引频次累积为0，洛伦兹曲线左端的相应部分与横轴重合，因此，曲线与横轴的分离点反映了未被引用载文在全部载文中所占的比例，即零被引率。影响因子较低的AmJPhys和MoscUPhysB+各年度G均大于0.68(表2)，引用分布不均匀程度较高，其零被引率均在50%以上(图3～7)，影响因子仅由不足半数的载文支撑。其中，MoscUPhysB+在2011年度的影响力甚至仅由约10%的载文产生，G高达0.892。虽然AmJPhys和MoscUPhysB+有较小的标准差，但其被引载文不足总量的50%，篇均被引频次也难以真实地代表载文的整体影响力。

表2 2011—2015年度7种物理期刊影响因子IJIF、基尼系数G及修正后的影响因子IJIFG

图3 2011年度洛伦兹曲线

图4 2012年度洛伦兹曲线

图5 2013年度洛伦兹曲线

图6 2014年度洛伦兹曲线

图7 2015年度洛伦兹曲线

基于上述期刊样本可知，被引频次在载文间既非均匀分布，也非正态分布，这意味着影响因子存在不同程度的失真，载文被引频次的标准差越大或者零被引率越高，期刊篇均被引频次的代表性就越低。

2.4 影响因子的失真与修正

一般认为，影响因子越高，总被引频次在载文间的分布越不均匀[10]，基尼系数越大。由图8(a)、(b)可知，PhysRevLett的影响因子小于NatPhys，但前者的基尼系数却大于后者；在这7种期刊中，RevModPhys、NatPhys和PhysRevLett既是影响因子最大，也是基尼系数最小的3种期刊。这表明影响因子并不与基尼系数同向变动，影响因子的失真程度与影响因子大小无关。

综上所述，总被引量在载文间的非均匀分布导致影响因子存在不同程度的失真，基尼系数G越小，分布越均匀，影响因子的代表性越高。因此可考虑将表征分布均匀程度的(1-G)作为基尼修正系数对影响因子进行修正，修正后的影响因子IJIFG可表示为

IJIFG=IJIF×(1-G)。

(3)

就本研究的虚拟案例，M刊的100次被引量均匀分布在100篇载文中，因此G为0，修正后的影响因子IJIFG仍为1。N刊的100次被引量仅集中在1篇载文，G为0.99，修正后的影响因子IJIFG降至0.01。笔者认为，基尼修正系数可有效地修正由于引用的偏态分布而产生的影响因子失真问题。图8(b)、(c)分别为前述7种期刊修正前、后的影响因子，修正后的影响因子均不同程度变小，具体数值见表2。其中，RevModPhys、NatPhys和PhysRevLett修正后影响因子的差距明显缩小。在科研管理中，如果单纯根据期刊影响因子奖励科研人员，则可能因引用的偏态分布产生激励不当的问题。

图8 2011—2015年度7种期刊的基尼系数与修正前后的影响因子。(a)G；(b)IJIF；(c)IJIFG

3 结语

期刊影响力源于期刊载文影响力，表征期刊影响力的指标应充分考虑期刊载文的整体影响力。影响因子所要求的分布条件在现实中难以保证，当被引量呈偏态分布，尤其大部分被引量集中于少数载文时，以影响因子表征的期刊影响力则出现失真，从而高估了期刊的影响力。从本研究的7种期刊样本看，被引量在载文间均呈右偏分布，基尼系数均在0.4以上，因此对期刊影响力的评价应考虑被引量在载文间的分布状况。笔者认为，引入基尼修正系数对影响因子进行修正，将有助于更真实地反映期刊的学术影响力，但修正后的实际效果还有待系统的实证检验。

[1] Garfield E. The history and meaning of the journal impact factor[J].TheJournaloftheAmericanMedicalAssociation,2006,295(1):90-93.

[2] Martin B R. Editors′ JIF-boosting stratagems: Which are appropriate and which not?[J].ResearchPolicy,2016,45(1):1-7.

[3] Stephan P,Veugelers R,Wang J. Reviewers are blinkered by bibliometrics[J].Nature,2017,544(7651):411-412.

[4] Vanclay J K. Impact factor: Outdated artifact or stepping-stone to journal certification?[J].Scientometrics,2012,92(2):211-238.

[5] 毛国敏,蒋知瑞,任蕾,等. 期刊信息量和影响力分布的不均匀性分析研究[J]. 中国科技期刊研究,2012,23(3):377-382.

[6] 俞立平,刘爱军. 指标数据分布与内部差距对学术期刊评价的影响:以JCR数学期刊为例[J]. 图书情报工作,2014,58(21):105-110.

[7] Weale A R,Bailey M,Lear P A. The level of non-citation of articles within a journal as a measure of quality:A comparison to the impact factor[J].BMCMedicalResearchMethodology,2004,4(1):14.

[8] Metze K. Bureaucrats,researchers,editors,and the impact factor-a vicious circle that is detrimental to science[J].Clinics,2010,65(10):937-940.

[9] Bornmann L,Mutz R,Neuhaus C,etal. Citation counts for research evaluation: Standards of good practice for analyzing bibliometric data and presenting and interpreting results[J].EthicsinScienceandEnvironmentalPolitics,2008,8(1):93-102.

[10] Stegmann J,Grohmann G. Citation rates,knowledge export and international visibility of dermatology journals listed and not listed in the Journal Citation Reports[J].Scientometrics,2001,50(3):483-502.