改进EFG法用于旋转梁的刚柔耦合动力学研究

谢丹 蹇开林

摘要： 采用全域插值广义移动最小二乘（IGMLS）的改进无网格伽辽金（EFG）法，对旋转中心刚体柔性梁系统的刚柔耦合动力学特性进行研究。利用考虑了柔性梁横向变形引起的非线性耦合项的一次近似耦合模型，根据Hamilton 原理和EFG离散方法得到刚柔耦合系统的无网格动力学离散方程。在大范围运动未知的情况下，采用数值方法对刚柔耦合系统进行动力响应的仿真计算，并对EFG法的主要影响因素进行了讨论分析。通过与有限元法的数值计算结果对比，验证EFG法用于刚柔耦合系统动力学研究的有效性及可行性，并为无网格法用于更复杂的柔性多体动力学的研究提供了理论依据。关键词： 多体动力学； 刚柔耦合； 旋转梁； 无网格伽辽金（EFG）法； 广义移动最小二乘（GMLS）

中图分类号：O313.7文献标志码： A文章编号： 10044523（2017）04052708

DOI：10.16385/j.cnki.issn.10044523.2017.04.001

引言

作为柔性多体动力学的一种典型模型，旋转梁的动力学特性已被广泛而深入的研究，包括附着在运动基上的结构动力学问题（或动力刚化问题）以及大范围运动情况未知的刚柔耦合动力学问题[17]。在柔性多体动力学的研究中，柔性体变形场的离散方法是其中的一个关键问题，根据目前的国内外研究，对柔性体变形场的离散主要采用的是假设模态法和有限元法[4，5]。其中，假设模态法由于依赖已知结构的振动振型而使其应用往往限于简单结构，有限元法虽具有很强的通用性，其表现出的固有缺陷则源于对单元或网格的依赖。

近年来，无网格法[8]以其独特的优势得到了国内外各领域学者的研究。它通过一组无需事先定义、散布在问题域及边界上的节点来表示问题域及边界，然后用场节点来构造近似的总体函数，可以彻底或部分的消除網格。有限元法采用预定义的单元构造形函数，所有单元的形函数是相同的；而无网格法的近似函数采用的是定义在局部支持域中的紧支函数，任意计算点的形函数仅通过包含在其支持域内的场节点来构造，计算点处的形函数可随计算点的变化而变化。因此，形函数的构造差异是无网格法与有限元法的本质区别。目前主要的无网格法有：无网格伽辽金（EFG）法[9]、径向点插值法（RPIM）[10]及再生核粒子法（RKPM）[11]等。无网格法的研究虽已被用于各种领域[1216]，但无网格法在多体动力学中的研究鲜有报道。文献[17]采用点插值法对旋转悬臂梁的弯曲振动及非惯性系下的结构动力学特性进行了分析，忽略了大范围运动对变形运动的影响。

众多无网格法中，EFG法以其高精度及简明的变换关系得到了广泛的研究与应用[1516]，但传统EFG法由于基于移动最小二乘近似（MLS）[18]，位移及导数边界的施加比较困难[1920]。本文采用全域插值的广义移动最小二乘近似（IGMLS）对柔性梁的变形场进行离散，在保持EFG法高精度的同时，使其位移及导数边界条件的施加像有限元法一样直接简单。在此基础上，采用考虑了非线性耦合项的一次近似模型[5]，对大范围运动未知情况下的旋转中心刚体柔性梁系统的刚柔耦合动力学特性进行了数值研究，并通过与有限元法对比，论证了EFG法用于刚柔耦合动力学研究的可行性。

1刚柔耦合系统运动学及变形描述

假定系统中的柔性梁采用的是Euler梁模型，材料均匀且各向同性，梁上的各处的横截面积均相等，不计重力影响。

图1为中心刚体悬臂梁系统，中心刚体绕Z0轴转动，研究系统的刚体运动和悬臂梁在O0X0Y0平面内的运动与变形。其中： O0X0Y0Z0为固定坐标系（右手定则），其原点与中心刚体的回转中心重合，OXY为固结在梁端点的浮动坐标系。梁的中性轴线上任意一点P0发生变形后的位置为P，rA为浮动坐标系原点O在固定坐标系下的位置矢量，h为P0在浮动坐标系下的位置矢量，u为P相对P0的变形位移矢量，r为P在固定坐标系下的位置矢量。相关几何尺寸及物理参数表示如下：a为中心刚体的半径，JH为中心刚体关于Z0轴的转动惯量，L为柔性梁未变形前的长度，ρ为梁的体积密度，A为梁的横截面积，E为材料的弹性模量，I为梁的横截面关于中性轴（Z轴）的惯性矩，τ为作用在中心刚体上的驱动力矩（力偶矩矢量沿Z0轴），θ为中心刚体作大范围旋转运动的角位移。

图1旋转中心刚体柔性梁系统物理模型

Fig.1The physical model of rotatinghub beam system

第4期谢丹，等：改进EFG法用于旋转梁的刚柔耦合动力学研究振 动 工 程 学 报第30卷在惯性坐标系下，梁中性轴线上任意一点P的位置矢量r对应的坐标向量为r=rA+Θ（h+u）（1）其中：h=x，0T （2）

Θ=cosθ-sinθ

sinθcosθ （3）

rA=acosθ

asinθ=aΘe0 （4）

u=u1

u2=ω1+ωc

ω2（5）式中e0=1，0T，式（5）为一次近似耦合模型的变形位移表达式，ω1与ω2分别为梁中轴线上一点沿X轴的位移和沿Y轴的位移（即横向变形），ωc=-12∫x0（ω2x）2dx为梁横向变形引起的轴向缩短量，即耦合变形量[5]，若不考虑该耦合变形量，则为零次近似模型。

对式（1）求导，得到点P的速度向量（绝对速度在固定坐标系下的投影）=A+Θ（h+u）+Θ （6）对式（6）求导，得到点P的加速度矢量（绝对加速度在固定坐标系下的投影）=A-2Θ（h+u）+2Θ+Θ+

Θ（h+u）（7）式中=0-1

10（8）系统动能的变分δT=-JHδθ-∫L0ρAδrTdx （9）考虑非线性应变位移关系式εxx=u1x-y2u2x2+12（u2x）2，得到势能的变分δΠ=∫L0EAω1xδ（ω1x）dx+∫L0EI2ω2x2δ2ω2x2dx（10）作用在系统上的外力的虚功δWF=τδθ（11）2系统刚柔耦合动力学离散方程2.1全域插值广义移动最小二乘（IGMLS）近似假设欧拉梁的求解域0≤x≤L被用N个场节点xI（I=1， 2，…，N）离散，根据EFG方法，挠度变量v（x）在全求解域内的近似表达式为vh（x）=∑mj=1pj（x）aj=pT（x）a （12）式中a=a1，a2，…，amT为待定参数向量， p（x）=1，x，x2T为m=3时的基函数向量。

则挠度函数及一阶导数（转角）的近似值在各节点处误差的加权平方和为J（a）=∑NI=1ωI（x）vh（xI）-vI2+

θh（xI）-θI2=

∑NI=1ωI（x）∑mj=1pj（x）aj-vI2+

∑mj=1dpj（x）dxaj-θI2（13）式（13）中的权系数ωI（x）=ω（x-xI），以下为本文采用的三次样条权函数的表达式ωI（r）=23-4r2+4r3，r≤0.5

43-4r+4r2+4r33，0.5

0，r>1（14）式中r=dIdmI，dI=‖x-xI‖是计算点x到节点xI的距离，节点影响域尺寸dmI=scale×cI，cI通常取节点xI与其最近的节点之间的距离，结构动力学分析中，影响域因子scale通常在2～4取值[19]。

根据GMLS近似，式（13）中的待定参数要使误差平方和最小，计算整理得A（x）a=B（x）（15）式中=1，2，…，N，1，2，…，NT（16）

A（x）=∑NI=1ωI（x）p（xI）pT（xI）+

dp（xI）dxdpT（xI）dx（17）

B（x）=B（0）（x）B（1）（x）

B（0）（x）=ω1（x）p（x1）…ωN（x）p（xN）

B（1）（x）=ω1（x）dp（x1）dx…ωN（x）dp（xN）dx （18） 将式（15）代入（12）得到梁的GMLS形函数，即Ω（1×2N）=ΦΨ=pT（x）A（x）-1B（x）（19）因此，基于节点位移参数的挠度及转角近似表达式为vh（x）=∑NI=1IvI+∑NI=1ΛIθI=Ω

θh（x）=∑NI=1I，xvI+∑NI=1ΛI，xθI=Ω，x （20）真实节点位移矢量d与节点位移参数矢量的关系d=Λ2（21）式中Λ2为转换矩阵，Λ（2N×2N） =

1 （x1 ） … N （x1 ） ψ1 （x1 ） … ψN （x1 ）

1 （xN ） … N （xN ） ψ1 （xN ） … ψN （xN ）

1，x （x1 ） … N，x （x1 ） ψ1，x （x1 ） … ψN，x （x1 ）

1，x （xN ） … N，x （xN ） ψ1，x （xN ） … ψN，x （xN ）（22）将式（21）代入式（20）得vh（x） = Ω =ΩΛ-12 d =N2d

θh（x） =Ω，x =Ω，x Λ-12 d= N2，x d（23）则梁的IGMLS形函数及其一阶导数表达式如下N2 =ΩΛ-12

N2，x =Ω，x Λ-12 （24）图2给出了梁离散后，中间节点的挠度与转角变量对应的标准GMLS形函数及IGMLS形函数曲线，由图可以明显看出IGMLS的全域插值特性。图2梁中间节点的GMLS形函数及IGMLS形函数

Fig.2Shape functions of GMLS and IGMLS at the middle point of the beam

2.2刚柔耦合动力学离散方程

假设N1（x）∈R1×N表示轴向位移的插值性移动最小二乘形函数（IMLS），N2（x）∈R1×2N表示上节推导的横向位移的IGMLS形函数，q1（t）∈RN表示节点纵坐标列向量，q2（t）∈R2N表示由挠度与转角组成的节点坐标列向量，表示如下q1（t）=u1（t），u2（t），…，uN（t）T

q2（t）=v1（t），…，vN（t），θ1（t），…，θN（t）T（25）梁的轴向、横向变形量及耦合变形量的离散表达式分别为：ω1（x，t）=N1（x）q1（t）（26）

ω2（x，t）=N2（x）q2（t）（27）

ωc （x，t） = -12qT2 S（x）q2 （28）式（28）中，S（x）为耦合形函数S（x） = ∫x0（N2 ′）TN2 ′dx （29）式中N2 ′表示对坐标x求偏导。

根据Hamilton变分原理，将相关离散变量代入，省略相关高阶项，考虑到δθ，δqT1 ，δqT2 的任意性，得到系统的刚柔耦合动力学无网格离散方程MθθMθq1Mθq2

Mq1θMq1q10

Mq2θ0Mq2q2

1

2+

2000

00Gq1q2

0Gq2q10

1

2+

000

0Kq1q10

00Kq2q2θ

q1

q2=

Qθ

Qq1

0+τ

0

0（30）式中：Mθθ = JH + Jb +qT1 M1 q1 +

qT2 M2 q2 + 2U11 q1 -qT2 D1 q2 （31）

Mq1θ=（Mθq1）T=-Rq2（32）

Mq2θ=（Mθq2）T=（U12）T+RTq1（33）

Mq1q1=M1（34）

Mq2q2=M2 （35）

Gq1q2=-（Gq2q1）T=-R （36）

Kq1q1=K1-2M1（37）

Kq2q2=K2+2（D1-M2）（38）

Qθ = -2（qT1 M1 1 + qT2 M2 2 +

U11 1 -qT2 D1 2 ） （39）

Qq1 = 2UT11 （40）式（31）中Jb=∫L0ρA（a+x）2dx為柔性梁的转动惯量。

式（31）～（40）中常数矩阵采用背景网格积分，以下给出部分矩阵的EFG法数值计算表达式：M1 = ∫L0ρANT1 N1 dx =

∑nck = 1∑ngi = 1ρAN1 （xQi ）TN1 （xQi ）iJik （41）

D1=∫L0ρA（a+x）S（x）dx=

∑nck=1∑ngi=1ρA（a+xQi）S（xQi）iJik（42）式中nc为用于积分的背景网格数目，ng 是每个背景网格内的Gauss积分点数，xQi为计算点坐标，i为第i个Gauss积分点的加权系数，Jik为第k个背景网格在计算点xQi处积分的雅克比矩阵。

3数值算例

对于刚柔耦合动力系统，通常外部作用力或力矩规律是已知的，而大范围运动量和梁的振动变形量均为求解量。不考虑阻尼影响，柔性梁的物理参数：长度L=1.8 m，横截面积A=2.5×10-4 m2，材料密度ρ=2.7667×103 kg/m3，弹性模量E=6.8952×1010 Pa，横截面的惯性矩I=1.3021×10-10m4。取中心刚体半径为a=0.05 m，转动惯量JH=0.3 kg·m2，作用在刚体上的外力矩为τ（t）=τ0sin（2πTt），0≤t≤T

0，t> T （43）式中T=2 s，按τ0=1 N·m和τ0=7 N·m两种情况进行数值仿真计算。

数值分析中，采用Newmark法对结构的非线性动力响应进行计算，时间步长取0.05 s，Newmark参数β=3/4，γ=1/2。有限元法采用9个单元离散，无网格法采用10个离散节点，且影响域因子取2.5，选择四点高斯积分。

3.1刚柔耦合动力响应分析

用FEM1表示采用一次近似模型的有限元法计算结果，EFG1表示采用一次近似模型的无网格法计算结果，EFG0则为采用零次近似模型的无网格法计算结果。

图3～6为τ0=1 N·m时的数值计算结果， 图3，4分别为刚体的角位移响应与角速度响应，图5，6分别为梁末端的横向、纵向位移响应。由图可看出，不论大范围旋转运动还是柔性体的变形运动，一次近似耦合模型下的无网格法与有限元法计算结果高

图3中心刚体转动角位移（τ0=1 N·m）

Fig.3The angular displacement of the hub when τ0=1 N·m圖4中心刚体的转速（τ0=1 N·m）

Fig.4The angular velocity of the hub when τ0=1 N ·m图5柔性梁末端的横向位移（τ0=1 N·m）

Fig.5The transverse displacement of the tip of the beam when τ0=1 N·m图6柔性梁末端的纵向位移（τ0=1 N·m）

Fig.6The axial displacement of the tip of the beam when τ0=1 N·m度逼近。当外力矩撤销后，中心刚体大约在20.77°附近摆动，柔性梁末端的横向振动频率约为1.31 Hz，柔性梁的残余振动与中心刚体的转动相互激励，由于未考虑阻尼影响，相互影响的两种运动将一直保持下去，并且在变形运动中，梁末端的纵向位移远远小于横向位移。此外，不考虑耦合效应的零次模型在此情况下的计算结果也比较接近。

图7～10为τ0=7 N·m时的数值计算结果。与τ0=1 N·m时的计算结果相比，由于驱动力矩的增大，刚体的转速明显提升，柔性梁横、纵向位移的幅值也明显增大。在τ0=7 N·m下，基于一次模型的无网格法与有限元法的计算结果依然高度逼图7中心刚体转动角位移（τ0=7 N·m）

Fig.7The angular displacement of the hub when τ0=7 N·m图8中心刚体的转速（τ0=7 N·m）

Fig.8The angular velocity of the hub when τ0=7 N·m图9柔性梁末端的横向位移（τ0=7 N·m）

Fig.9The transverse displacement of the tip of the beam when τ0=7 N·m

图10柔性梁末端的纵向位移（τ0=7 N·m）

Fig.10The axial displacement of the tip of the beam when τ0=7 N·m近，中心刚体大约在147.1°附近摆动，柔性梁末端的横向振动频率约为1.31 Hz，大范围运动与变形运动的耦合效应明显，而零次模型则表现出很大的差异。进一步研究发现，随着驱动力矩增大，一次模型下梁末端的位移响应可以始终保持稳定，而零次模型在τ0=10 N·m时，数值结果发散。

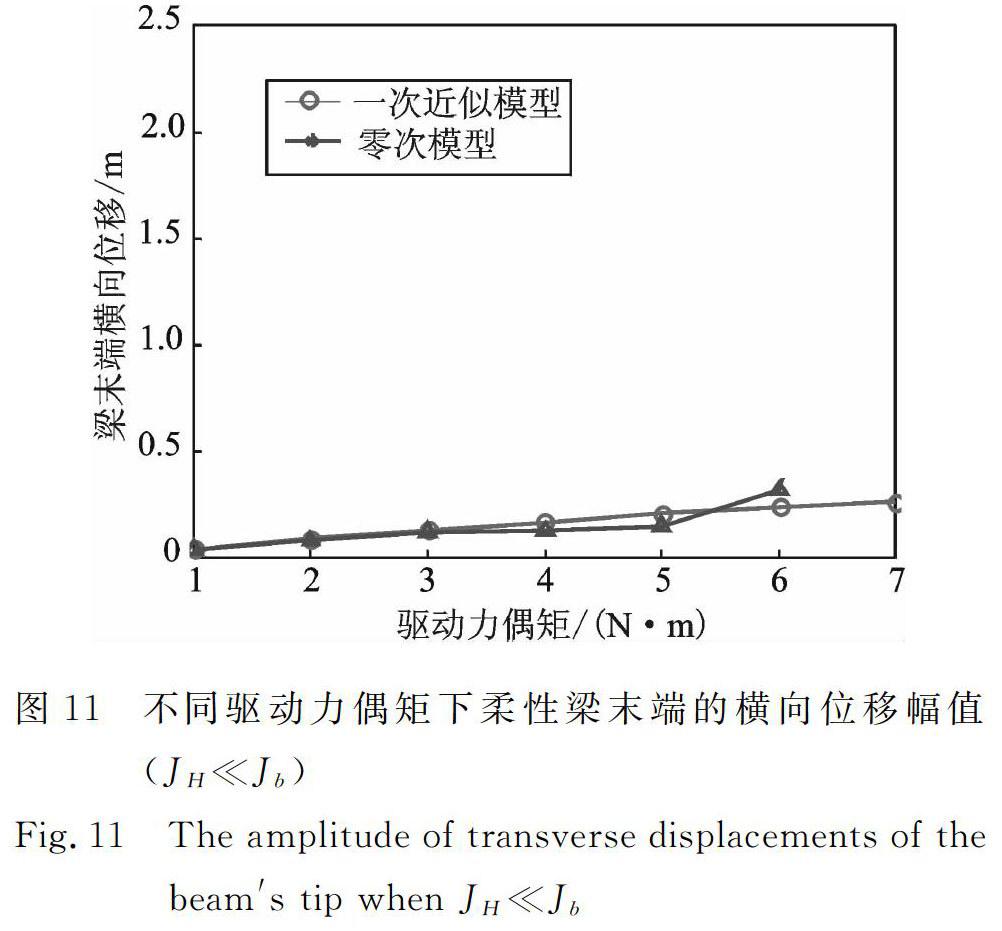
此外，由图7～10发现，零次模型下响应的结果不仅与一次模型有较大差异，而且其幅值相对一次模型的幅值偏小，这是由于该数值算例中所取的中心刚体的转动惯量（JH=0.3 kg·m2）远小于柔性梁的转动惯量（Jb≈1.46 kg·m2）的缘故。进一步研究发现，在零次模型发散之前，随着驱动力矩增大，当中心刚体转动惯量远小于柔性梁的转动惯量（JHJb） 时，零次模型下系统响应的幅值小于一次模型下的幅值（如图11所示）；当中心刚体转动惯量与柔性梁的转动惯量相当时（JH≈Jb），零次模型下的计算结果则偏大（如图12所示）；当中心刚体转动惯量远大于柔性梁的转动惯量（JHJb），零次模型与一次模型的响应幅值相近（如图13所示）。

图11不同驱动力偶矩下柔性梁末端的横向位移幅值（JHJb）

Fig.11The amplitude of transverse displacements of the beam′s tip when JHJb图12不同驱动力偶矩下柔性梁末端的横向位移幅值（JH≈Jb）

Fig.12The amplitude of transverse displacements of the beam′s tip when JH≈Jb

圖13不同驱动力偶矩下柔性梁末端的横向位移幅值（JHJb）

Fig.13The amplitude of transverse displacements of the beam′s tip when JHJb3.2影响因素分析

EFG法中的影响域因子及Gauss积分点数目对计算结果的影响分别如表1和2所示。表中，把FEM的计算耗时记作1，EFG法与FEM法的计算耗时的比值为计算相对耗时，为说明计算的效果，选择2 s时刻梁末端的横向位移的计算结果列于表中，位移相对误差则通过EFG-FEMFEM%计算得到。

由表1可以看出，随着影响域因子的增大，EFG法的计算耗时逐渐增多，但在所取的影响域因子范围内，EFG法的耗时小于有限元法。从2 s时刻梁末端的横向位移的计算误差来看，影响域因子对计算精度的影响不是很明显，也没有表现出特定的规律，说明EFG法在所取影响域因子范围内计算比较稳定，且在达到与有限元法相似的精度下，其计算效率高于有限元法。表1不同影响域因子下EFG法的计算相对耗时及横向位移误差

Tab.1The relative computational cost and computational error of EFG method based on different influence factors

离散

方式影响域

因子计算相对

耗时2 s时刻的末端

横向位移/m

（相对误差/%）FEM——1-0.0195（——）1.50.250-0.0196（0.513）2.00.296-0.0195（0.0）EFG2.50.312-0.0194（0.513）3.00.343-0.0186（4.615）4.00.530-0.0195（0.0）

表2 不同Gauss积分点数下EFG法的计算相对耗时及横向位移误差

Tab.2The relative computational cost and computational error of EFG method based on different Gauss integral points

离散

方式Gauss积分

点数目计算相对

耗时2 s时刻的末端

横向位移/m

（相对误差/%）FEM——1-0.0195（——）20.2340.054（376.92）EFG30.296-0.0195（0.0）40.310-0.0195（0.0）60.359-0.0172（11.79）70.390-0.0195（0.0）

由于近似函数构造方法的原因，无网格法的被积函数通常是有理式，一般情况下无法进行精确积分，采用Gauss积分的积分点数对计算结果有明显影响。如表2所示，随着积分点数的增多，计算耗时逐渐增加，不恰当的积分点的选取，还会造成很大的误差，如积分点取2和6时。通过本文的数值试验，通常Gauss积分点取4即可满足计算效率和精度的要求。

4结论

1）传统EFG法虽具有高的计算精度，但边界条件施加困难；改进后的EFG法通过采用全域插值的广义移动最小二乘（IGMLS）近似，在保持高计算精度的同时，使中心刚体旋转梁系统的位移及导数边界的施加像有限元法一样方便处理。

2）零次模型在作用力矩增大到一定值时出现发散，而一次模型保持稳定。EFG法证明了零次模型在刚柔耦合分析中的局限性以及一次近似模型的合理性。

3）EFG法中的影响域因子在1.0

参考文献：

[1]Kane T R， Ryan R R， Banerjee A K， Dynamics of a cantilever beam attached to a moving base [J]. Journal of Guidance， Control and Dynamics， 1987， 10（2）：139—151.

[2]Yoo H H， Ryan R R， Scott R A. Dynamics of flexible beams undergoing large overall motions [J]. Journal of Sound and Vibration， 1995， 181： 261—278.

[3]刘锦阳，洪嘉振. 刚柔耦合动力学系统的建模理论研究[J].力学学报， 2002， 34（3）：409—415.

Liu Jinyang， Hong Jiazhen. Study on dynamic modeling theory of rigidflexible coupling systems [J]. Acta Mechanica Sinica 2002， 34（3）： 409—415.

[4]蔡国平， 洪嘉振. 旋转运动柔性梁的假设模态方法研究[J].力学学报， 2005， 37（1）：48—56.

Cai Guoping， Hong Jiazhen. Assumed mode method of a rotating flexible beam [J]. Acta Mechanica Sinica 2005， 37（1）： 48—56.

[5]Yang H， Hong J Z， Yu Z Y， Dynamics modeling of a flexible hubbeam system with a tip mass[J]. Journal of Sound and Vibration， 2003， 266：759—774.

[6]章定国， 余纪邦. 做大范围运动的柔性梁的动力学分析[J].振动工程学报， 2006， 19（4）：475—480.

Zhang Dingguo， Yu Jibang. Dynamical analysis of a flexible cantilever beam with large overall motions [J]. Journal of Vibration Engineering 2006， 19（4）： 475—480.

[7]吴胜宝， 章定国. 大范围运动刚体柔性梁刚柔耦合动力学分析[J].振动工程学报， 2011， 24（1）：1—7.

Wu Shengbao， Zhang Dingguo. Rigidflexible coupling dynamic analysis of hubflexible beam with large overall motion [J]. Journal of Vibration Engineering 2011， 24（1）： 1—7.

[8]Belytschko T， Kronganz Y， Organ D， et al. Meshless methods： an overview and recent developments [J]. Computer Methods in Applied Mechanics and Engineering， 1996，139（1） ： 3—47.

[9]Belytschko T， Lu Y Y， Gu L. Elementfree Galerkin methods [J]. International Journal for Numerical Methods in Engineering， 1994， 37： 229—256.

[10]Gu Y T， Liu G R. A local point interpolation method for static and dynamic analysis of thin beams [J]. Computer Methods in Applied Mechanics and Engineering， 2001，190： 5515—5528.

[11]Liu W K， Jun S， Zhang Y F， et al. Reproducing kernel particle methods for structural dynamics[J]. International Journal for Numerical Methods in Engineering， 1995， 38： 1655—1679.

[12]Liu L， Chua L P， Ghista D N. Elementfree Galerkin method for static and dynamic analysis of spatial shell structures [J]. Journal of Sound Vibration， 2006， 295： 388—406.

[13]Singh I V， Tanaka M， Endo M. Thermal analysis of CNTbased nanocomposites by element free Galerkin method [J]. Computational Mechanics， 2007， 39： 719—728.

[14]Mirzaei D， Schaback R. Solving heat conduction problems by the Direct Meshless Local PetrovGalerkin （DMLPG） method [J]. Numerical Algorithms， 2014， 65： 275—291.

[15]Hajiazizi M， Bastan P. The elastoplastic analysis of a tunnel using the EFG method： A comparison of the EFGM with FEM and FDM [J]. Applied Mathematics and Computation， 2014， 234： 82—113.

[16]Zhang L W， Deng Y J， Liew K M. An improved element—free Galerkin method for numerical modeling of the biological population problems[J]. Engineering Analysis with Boundary Elements， 2014， 40：181—188.

[17]杜超凡， 章定國， 洪嘉振. 径向基点插值法在旋转柔性梁动力学中的应用[J]. 力学学报， 2015， 47（2）：279—288.

Du Chaofan， Zhang Dingguo， Hong Jiazhen. A meshfree method based on radial point interpolation method for the dynamic analysis of rotating flexible beams [J]. Chinese Journal of Theoretical and Applied Methanics 2015， 47（2）： 279—288.

[18]张雄， 刘岩. 无网格法[M]. 北京： 清华大学出版社， 2004.

[19]Cheng Y M， Bai F N， Peng M J. A novel interpolating elementfree Galerkin （IEFG） method for twodimensional elastoplasticity [J]. Applied Mathematical Modelling， 2014， 38：5187—5197

[20]Garijo D， Valenciaó F， GómezEscalonilla F J. Global interpolating MLS shape functions for structural problems with discrete nodal essencial boundary conditions [J]. Acta Mechanica， 2015， 226： 2255—2276.

An improved EFG approach for rigidflexible coupling dynamics

of the rotating hubbeam system

XIE Dan1， JIAN Kailin1，2

（1. College of Aerospace Engineering， Chongqing University， Chongqing 400044， China；

2. State Key Laboratory of Coal Mine Disaster Dynamics and Control， Chongqing 400044， China）

Abstract： Based on the global interpolating generalized moving least squares （IGMLS）， the improved elementfree Galerkin （EFG） method was applied to rigidflexible coupling dynamics of rotating hubbeam systems. With the firstorder approximate model including the nonlinear coupling term induced by the transverse deformation of the flexible beam， the elementfree dynamic equations were derived by the Hamilton principle and EFG method. Research on the rigidflexible coupling dynamics where the overall motion was unknown was conducted by numerical methods； meanwhile， the major influence factors of the EFG method were discussed. Numerical comparisons between the EFG method and the FEM verified the effectiveness and feasibility of the EFG method applied for rigidflexible coupling dynamics and this research provided a direction of elementfree methods for more complicated flexible multibody dynamics.Key words： multibody dynamics； rigidflexible coupling； rotating beam；elementfree Galerkin （EFG） method；generalized moving least squares （GMLS）作者簡介：谢丹（1987—），女，博士研究生。电话：158238266528；Email： xiedanv@163.com

通讯作者：蹇开林（1965—），男，博士，教授。电话：13220275685；Email：cqjian@cqu.edu.cn