第二十二讲 混料均匀设计简介
徐静安
在混料试验中,分量组分至少有3种,而每个分量组分Xi的含量百分比总和等于1,试验响应值Y仅与Xi的百分比有关,各个分量是不独立的。
过去,传统的试验研究把单因素考察作为研究方案的主体方法,现在的试验研究方案:单因素考察探索试验—多元素试验设计优化试验—稳定性验证试验。原因之一是单因素考察在简便,直观的同时存在一定的局限性。单因素考察应用时,实际上默认研究对象的各个因子之间试验不相关,各个因子对Y没有交互作用。
量大面广的混料配方试验,其各个分量是相关而不独立的,基于直角坐标的传统单因素方法,在混料配方试验中会造成分量间的隐性混杂。此外,传统方法在寻优效率等方面也受到极大挑战。所以,逐步开发并形成回归试验设计的各种方法。
一、混料回归设计的技术进展
对于混料配方试验方案,数理统计学家作出了很大努力。Scheffe在1958年在正单形坐标体系基础上提出了单纯形格子点法,1963年提出了单纯形质心法。Cornell提出了轴设计法,并在1990年对经典的混料设计作了综合介绍。
经典的混料设计讨论了分量组分无约束、下限约束、有上下限约束的试验设计及增强方案,采用全回归法统计建模。部分内容见本刊2018年第一期刊登的第二十一讲“混料配方研究中极端顶点设计的应用解读”。MINITAB软件相应模块支持经典的混料设计方案及计算。
在经典混料回归设计应用过程中,又发现了一些问题:(1)实验点(不同的配方)局部相对密集,也就是在考察范围内,点集TP布点不够均匀;(2)界面点过多,在无下限约束中,某些分量组分为零,缺少某组分的化学反应,或不起化学反应、或生成另一种产品。
发现问题和解决问题是创新的导向。
王元、方开泰于20世纪80年代初应用数论方法提出均匀设计。为了克服经典混料设计存在的问题,于1990年提出混料均匀设计。其中,有上、下限约束的混料均匀设计问题较为复杂。王元、方开泰先是按随机过程在蒙脱卡洛逆变换基础上进行布点,2000年改用条件分布方法。中国均匀设计学会有相应软件支持。
唐启义开发的数据处理系统(DPS)软件相应模块平衡了混料设计经典方法的统计优良性和试验点分布均匀性,用均方误差准则(MSE)开发了定向优化算法。上海化工研究院技术开发中心已购置正版DPS数据处理系统软件给以支持。
二、混料均匀设计
基本思想是将n个试验点(n种不同的配方)均匀地分布在TP上。对于混料中分量P个组分无约束的混料均匀设计相对简单,DPS等软件均采用方开泰等提出的逆变换方法构筑设计方案。具体步骤如下所示:
(1)根据考察的分量个数P,选定的实验方案实验次数n,选择等水平均匀设计表Un*(nl)或Un(nl)。均匀设计表所能安排的因素个数l一般要大于考察的分量个数P,根据使用表选择P-1列进行变换。
(2)用 {qji}表示所选均匀表第j列中的第i(i=1,2,…,n)个元素(水平数而不是具体的水平值)进行转换。
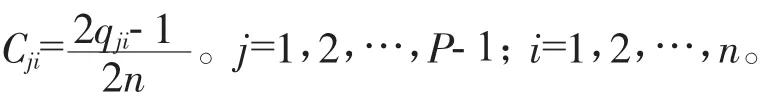
(3)将{Cji}转换成{Xji}
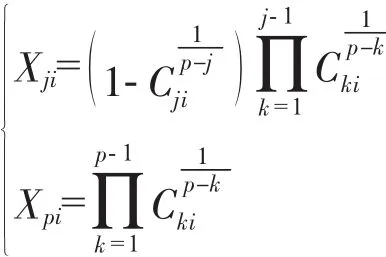
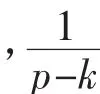
于是 {Xji}就给出了对应TP的配方均匀设计方案,并用代号UMn(np)或UMn*(np)表示,对于分量无约束的混料均匀设计,有关专著、软件均采用此变换。《试验设计与数据处理》(李云雁、胡传荣编著)附录给出了系列UMn(np)、UMn*(np)配方均匀设计表供选择。DPS软件在“试验设计”——均匀设计“——混料均匀设计”功能模块中均能获得相应的混料均匀设计方案。
为何要对常用的均匀设计表进行这样的变换?
Un(nl)或Un*(nl)均匀设计表适用于多维空间的直角坐标系均匀布点。而混料试验∑Xi=1,其分量是不独立的,适用于多维空间的单形坐标系,经过上述变换,UMn(np)、UMn*(np)混料均匀设计表才能体现在单形坐标系中的均匀布点。
为了直观了解变换过程及变换效果,对其进行进一步解读;
对于P=3,n=7的案例,可选方案U7*(74),根据U7*(74)使用表,(P-1)=2,选1,3两列,即对U7*(72)两列进行变换(见表1、表2)。
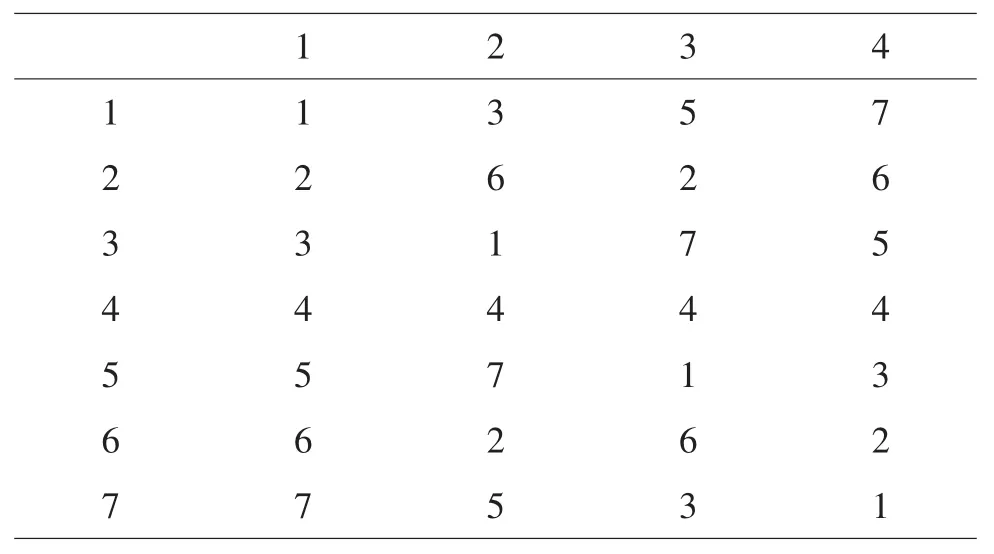
表1U7*(74)

表2U7*(74)的使用
对于P=3,上述变换计算可简化成如下形式:
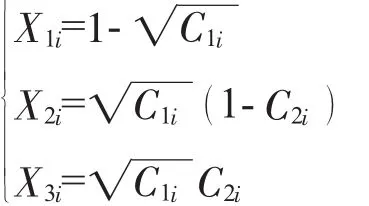
当i=1时,表中第1列第1个元素q11=1,而选中的第2个分量列的第1个元素q21=5,可得:
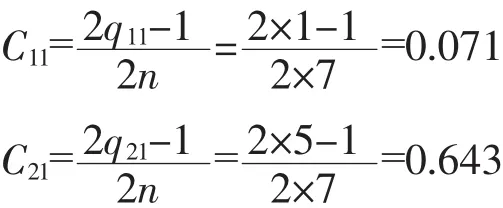
进一步计算:
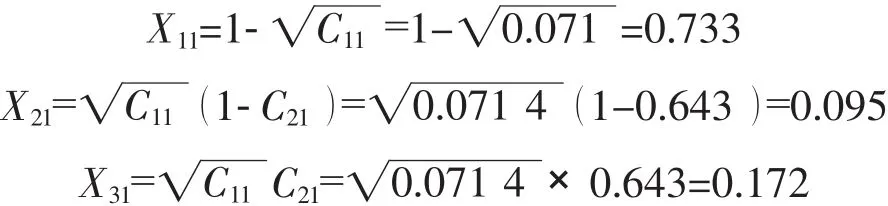
同理,可通过计算得到{Xji},形成表3。
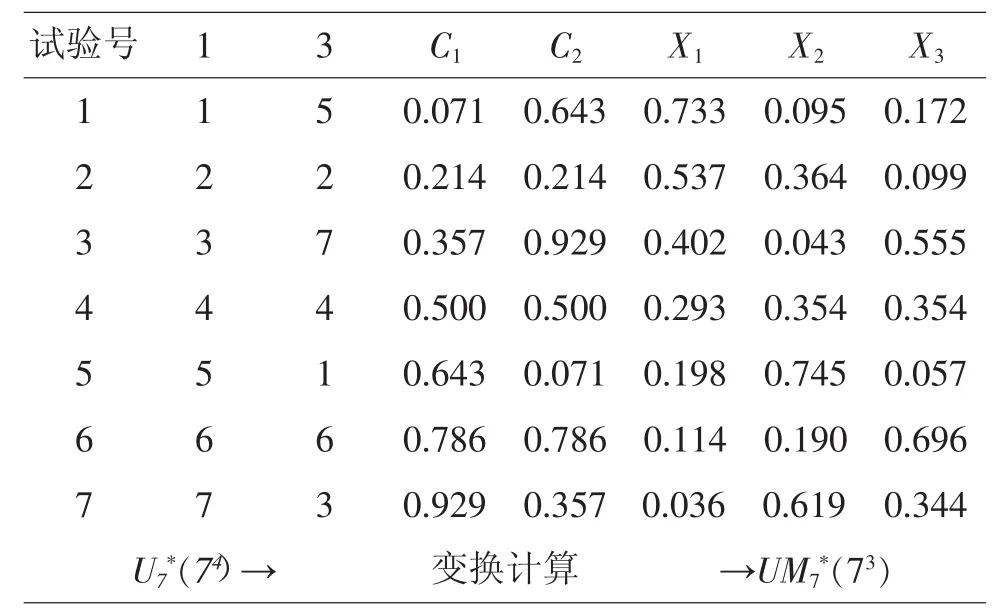
表3UM7*(73)及其形成过程
经变换计算,X1+X2+X3≈1,对试验结果影响不大。具体计算已由专用软件完成,对我们应用者而言,知其然,也知其一点所以然。需要强调的是,对分量无约束的混料回归设计,在变换成混料均匀设计时,对∑Xi=1中各分量是一视同仁的。但在统计建模时,(P-1)变换时选中的分量进入模型。
进一步分析变换方案效果:对于{p,d}={3,2}的经典混料回归设计,单纯形质心法试验设计方案见表4。
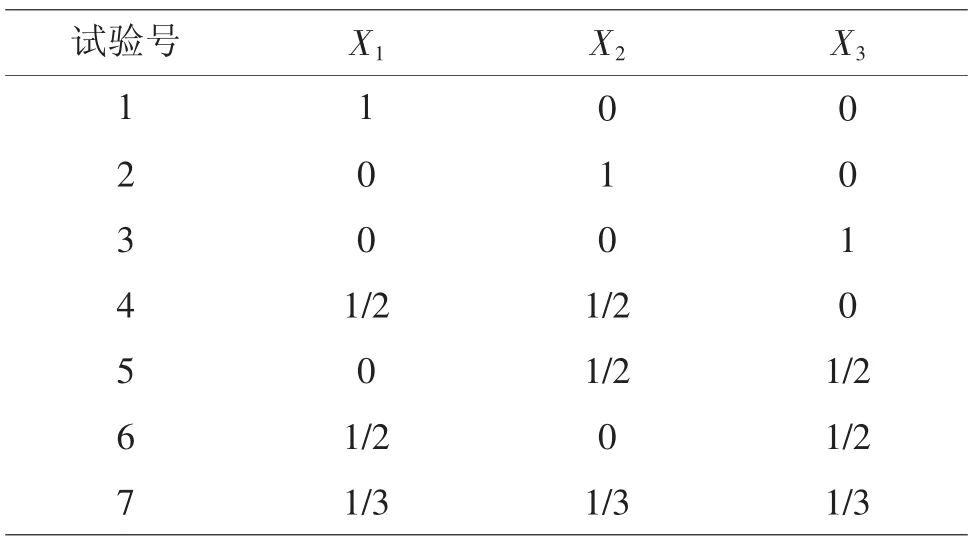
表4 单纯形质心法试验设计
上述方案中,7组试验中有6组试验出现分量为“0”,除了7号试验,6组试验的布点均为界面点,对涉及化学反应的混料试验,从专业知识上也难以接受。此外,7次试验仅对Xi分量考察了4个水平,效率也不是很高。
曾经设想把X3作为“陪衬”,直接将X1,X2按独立变量进行均匀设计选表而不进行变换,具体试验方案中按X3=1-X1-X2求取。选U7*(74)表中1,3列,结果见表5。
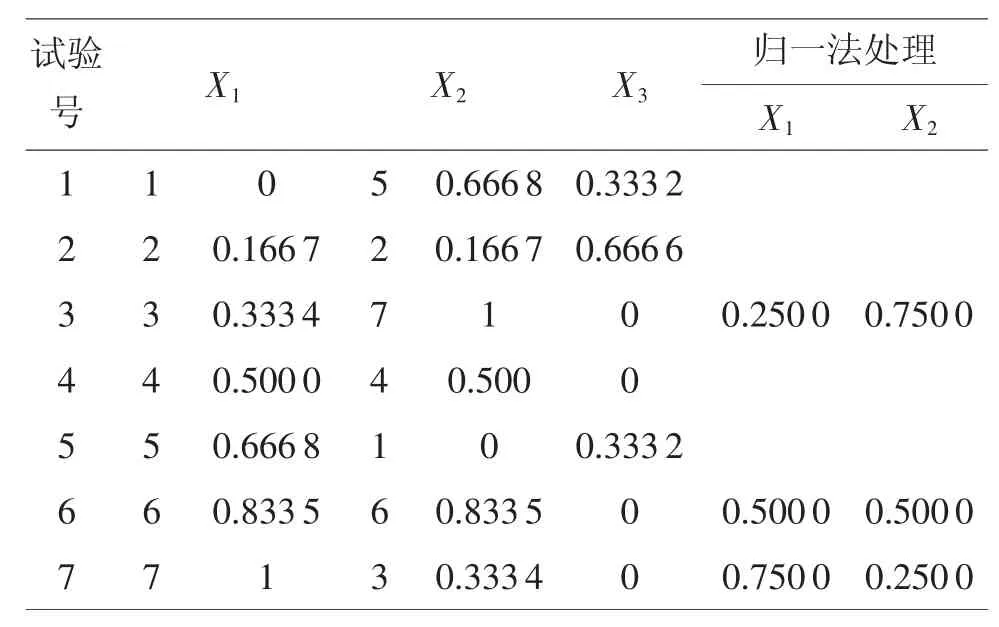
表5 U7*(74)的应用及结果
上述方案中,7组试验有2组分量为“0”(X1,X2),如果总体分析,计及 X3,仍有 6 组分量为“0”。此外,3、6、7号试验归一化处理后,也较大地影响了U7*(74)表的均匀性,且X3亦仅考察了3个水平,此方案也不理想。为此,开发了UMn(nP)混料均匀设计表,见图 1~3。
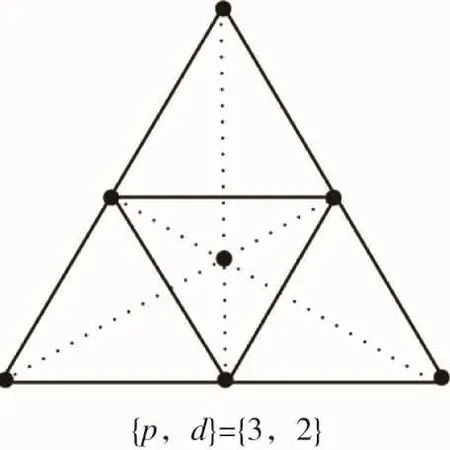
图1 经典混料回归设计的单纯形质心法布点
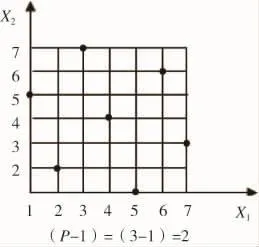
图2U7*(74)均匀设计布点图

图3混料均匀设计UM7*(73)布点图
三、有约束的混料均匀设计
在实际混料试验中,除了∑Xi=1的约束条件,各分量还受上下限约束,如 0≤ai≤xi≤bi≤1,i=1,2,…,p。
本文先行讨论有下界约束的试验设计。
有下界约束的单纯形设计在单形坐标系中能准确描述混料组分间的关系,一般用正单形,如正三角形、正四面体、……,P维单形即(P-1)的单纯形。为便于讨论,以P=3,P-1=2维的平面单纯形为例,给以各分量下界约束ai,如图4所示。
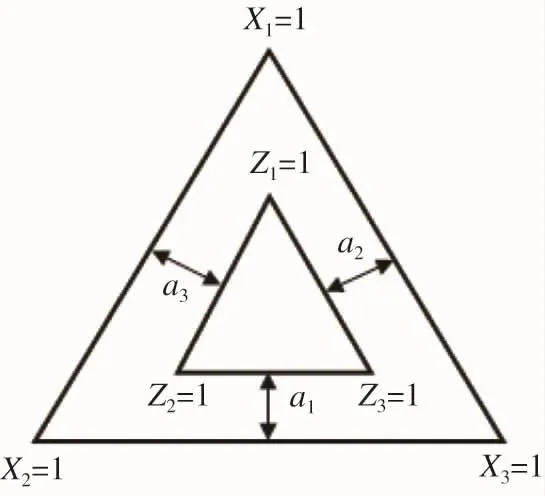
图4 有下界约束的单纯形配方设计
由图4可见,有下界约束的单纯形试验范围形成了一个小的单纯形,也就是在对各分量给以下界约束的同时,也转化为对相应分量的上界约束。
此时自然变量Xi转换成规范变量(编码值)或称为“拟分量”Zi。转换公式为:
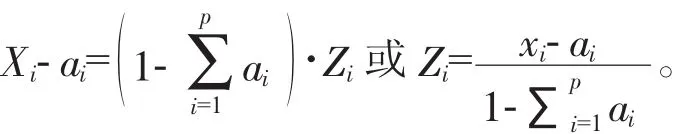
其中 ,Xi≥ai,∑ai<1。
可以认为上述转换对多分量正单形都是适用的,相关专著讨论至此,仍转入经典的混料格子点设计。笔者认为,按照类比思维仅有下界约束的正单形试验范围转化为一个小的正单形,可通过拟分量Zi转化为无约束的正单形混料均匀设计,即可选用UMn*(np)或UMn(np)混料均匀表。
相关专著及软件对此转换功能尚未充分挖掘,值得探索应用。这样构筑的混料均匀设计有良好的试验设计性质。从应用角度来看,这是本讲座开发的新的知识点。
按照发散思维,进一步引伸在混料试验中,分量受上下限约束是通常遇到的工程问题。在正单形坐标系中,图5所示对各分量给以ai下限约束,以P-1=3-1=2的正单纯形为例,转化为对各分量的上限约束,则:
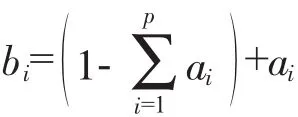
中学的平面几何即可证明:
所以实际混料试验的上下限约束,如果能调整到符合上述约束条件,仍能形成拟分量Zi无约束的正单形,方便地使用混料均匀设计表。
四、案例
试制某种火箭推进剂,三种混料成分受下限约束。
黏结剂 X1≥0.2;氧化剂 X2≥0.4;燃料 X3≥0.2。
试验目的为:混料配方弹性模数大于3000,并且黏结剂用量尽可能少。
弹性模数亦称“弹性模量”或“弹性系数”,是材料在弹性极限内应力同应变的比值,反映材料抵抗应变的能力。材料的弹性极限随温度的升高而减小。显然,本案例是在固定过程参数温度的条件下进行配方混料设计。这是一个典型的有下界约束的混料试验问题。其实验考察范围是在P-1=3-1=2的单纯形中形成的小正三角形,由于a1=0.2,a2=0.4,a3=0.2,1-∑ai=1-(0.2+0.4+0.2)=0.2<1,所以考察范围内小正三角形内任意一点的坐标关于自然空间与编码空间之间的转换关系为:
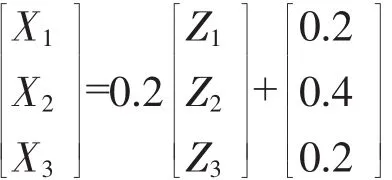
在实际试验时,假定采用不同的方案。
(1)单配方考察试验,即传统的混料试验方案
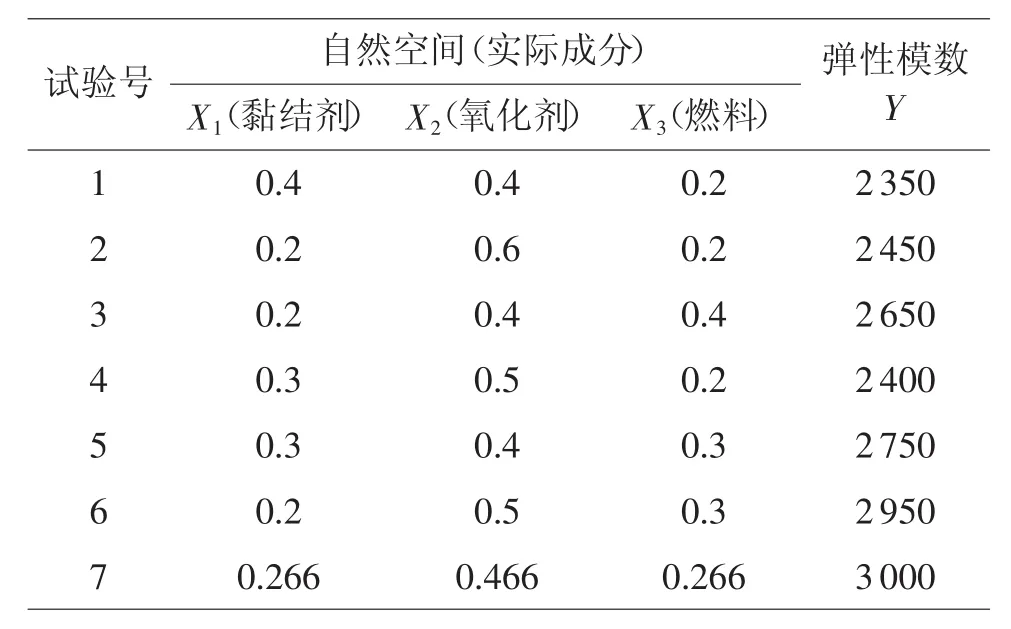
表6 单配方考察试验结果
通过7次单配方的考察,7号试验的弹性模数为3 000,考虑到误差,要求Y>3 000,尚应在7号试验Xi附近追加试验。由于混料试验分量不独立,难以单独判断分量的“好点”方向。所以需在此基础上追加2×P组单配方考察试验,工作量相对较大。而在相同试验次数下,可提取的信息量有限,试验效率不高,特别是对专业知识经验的依赖性更强。
(2)单纯形质心设计,即经典的混料设计方案
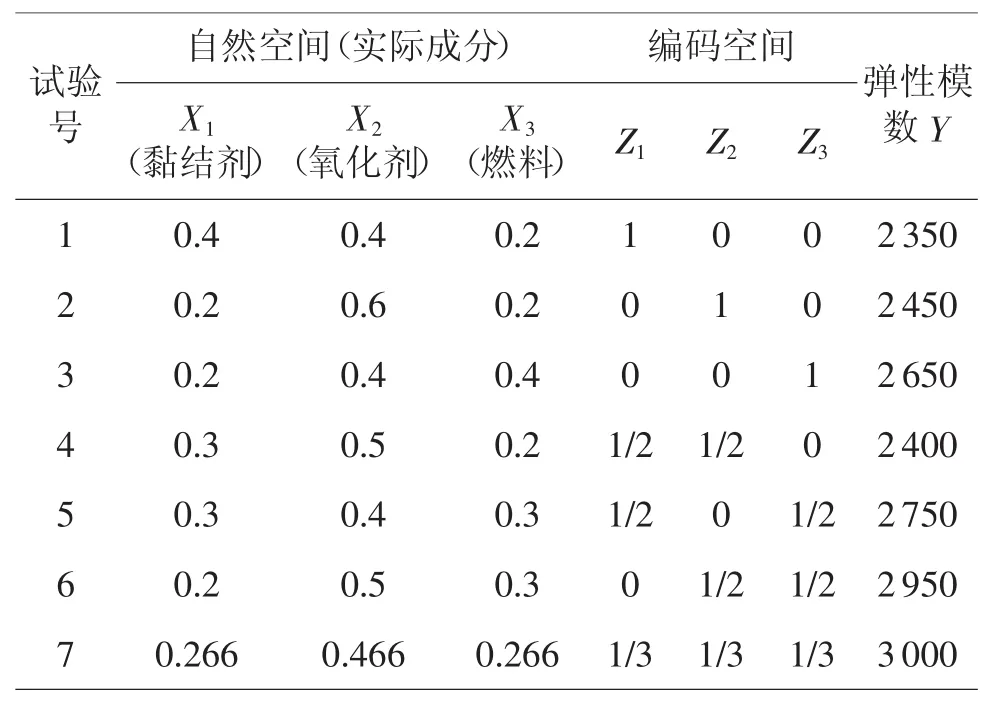
表7 单纯形质心设计结果
上述构成经典的{p,d}={3,2}三分量二阶单纯形质心设计,可用Scheffe不完全三次多项式拟合,求得Y对编码“拟分量”的全回归方程。因本文重点并非讨论经典三分量二阶单纯形质心设计,限于篇幅计算过程略,有兴趣的读者可查阅相关资料。读者应用时,MINITAB,DPS有相应模块计算支持。
可得:Y=2 350Z1+2 450Z2+2 650Z3+1 000Z1Z3+1 600Z2Z3+6 150Z1Z2Z3
此编码三分量混料体系的约束条件:
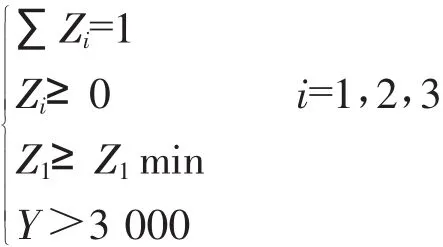
对上述Scheffe多项式全回归方程作个说明,方程中缺 Z1Z2项,经过笔者计算验证:b12=4Y12-2(Y1+Y2)=4×2 400-2×(2 350+2 450)=0,所以该项可略。对混料设计的结果进行分析,由于分量不独立,应在单形坐标系中的Y等值线图上进行。按满足Z1≥Z1min 选择混料优化点配方:Z1=0.05,Z2=0.41,Z3=0.54,预报Y=3 002.24,相对应的自然分量X1=21%、X2=48.2%、X3=30.8%,验证值为Y=3 010。
经典的单纯形质心设计比传统的单配方试验效率大为提高,数据处理更加规范、可行。
(3)混料均匀设计,即现代混料设计方案
UM7*(73)及其生成过程如表8所示。
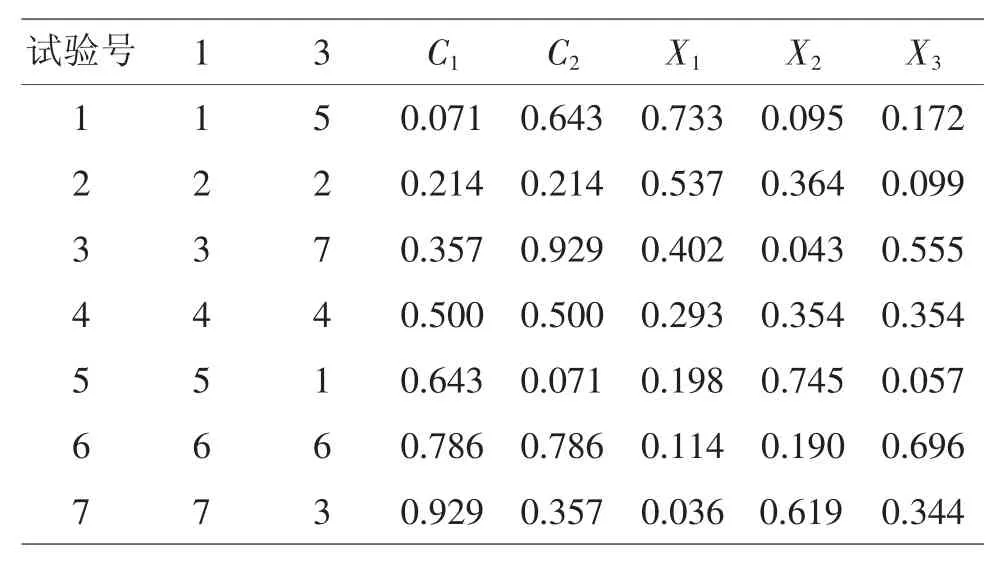
表8UM7*(73)及其生成过程
从U7*(72)均匀表逆变换成混料均匀设计表UM7*(73),本文已前述,可直接查表及在DPS软件模块中生成。需要说明的是,UMn*(nl)适用于混料无约束及约束可形成正单形的场合。当约束形成正单形时,表中Xi应由“拟分量”Zi替代。结合本案例,选用UM7*(73)表后,具体的试验方案(见表9),需从编码空间Zi转换成自然空间的Xi。
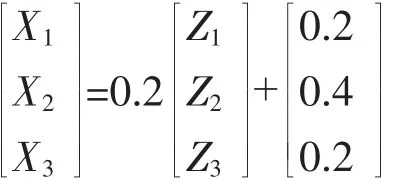

表9 UM7*(73)具体的试验方案
在相同的实验样本量n=7次条件下:传统单配方考察,考察分量4个水平,难以建模,尚需追加实验;经典单纯形质心设计,考察分量4个水平,可以建模,但边界点过多;现代混料均匀设计考察分量7个水平,均匀性更好,可以建模。本讲座第一讲“统计模型的假定和变量水平的设定”,已证明在相同的条件下,多水平设计比重复水平设计效率更高,模型稳定性更好。对本文讨论的内容作一简单归纳,混料均匀设计方案构筑,建模及变换的逻辑框图见图6。
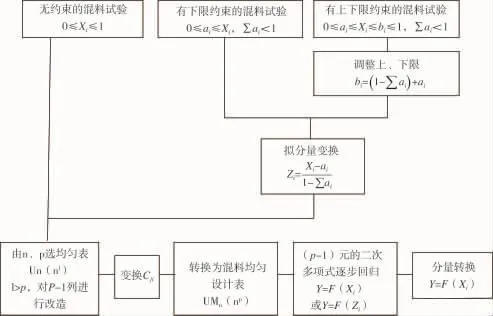
图6 混料均匀设计方案构筑、建模及变换的逻辑框图
借用中央人才工作协调小组指导的《中国人才》2014年10月刊(总第463期)中“退让的智慧”一文中的一段话,与君共勉。寒山曾问拾得:“世间谤我、欺我、辱我、笑我、贱我、恶我、骗我,如何处治乎”?拾得说:“只是忍他、让他、由他、避他、耐他、敬他、不要理他,再待几年且看他。”静心做好该做、想做的事。在创新开发中,学习应用新技术不可避免地会有坎坷、挫折甚至失败,会因被误解、低估而感到孤独。青年同仁们,当前的科研环境已经有了很大变化,但仍需忍耐、坚持,不断学习应用新技术、新方法。
“混料配方研究中极端项点设计的应用解读”介绍的是经典方法,本文介绍的是能形成正单形的现代混料均匀设计。对于上、下限约束不能形成正单形的混料均匀设计,将在后续讨论,让我们同行。

