基于证据理论的列控中心TSR处理功能安全性评估

郭盛楠,武晓春

(兰州交通大学自动化与电气工程学院,兰州 730070)

高速铁路具有运行速度快、正点率高、输送能力大和能源消耗低等优势，是当今社会的一种新型运输方式，其中列控中心(Train Control Center，TCC)是铁路中CTCS-2级地面子系统中的核心设备，它承担着确保行车安全的重要职责，对其进行安全性评估意义重大。国外铁路安全评估体系研究较早，已有了较丰富的评估经验，国内学者以我国实际情况为背景，通过借鉴国外经验也逐渐提出符合我国国情的安全评估方法和体系[1-3]。目前，故障树分析法(Fault Tree Analysis， FTA)、模糊层次分析法、模糊综合评判法、贝叶斯网络模型等方法已经在安全性评估领域广泛应用[4-7]。对于复杂系统的安全评估，多采用故障模式及效果分析(Failure Mode And Effects Analysis，FMEA)方法。但实际情况下，仅仅使用FMEA方法进行安全评估会存在一些不足，致使其评估精度下降，应用受到一定阻碍[8]。

首先，FMEA是建立在一定的数据资料基础上，多依靠专家背景用主观语言描述出来，风险数据有限且具有主观不确定性。本文提出的证据理论在处理数据资料有限和不确定信息上具有突出优势，能够识别和修正冲突证据，并重新确定其权重[9-11]，从而将不同专家的意见进行融合，增加了数据的真实性，在专家评估系统和数据融合领域得到广泛应用。

其次，FMEA是通过计算风险顺序数(Risk Priority Number，RPN)来实现系统的安全性评估。一般来说，RPN是发生度(Occurrence Probability Ranking，简称“O”)、严重度(Effect Severity Ranking，简称“S”)、检测度(Detection Difficulty Ranking，简称“D”)三者等比例相乘。在实际计算中，FMEA不仅忽略了3个风险因子的权重，而且对于系统中风险影响不同的风险因素，其O、S、D相乘也可能会得到相同的RPN，从而导致其评估结果存在一定偏差。结合证据理论对专家评估结果修正处理后，不仅能够确定风险因子O、S、D的权重，也会避免不同风险因素的RPN值相同，提高计算的精准性。计算过程的基本流程如图1所示。

图1 基于证据理论方法的流程

1 证据理论

证据理论是一种广泛应用的不确定性推理方法，它建立在识别框架、基本信度分配函数等概念的基础上。将每个专家的打分结果都视为一个证据，利用证据理论来识别冲突证据，再将证据之间的可信度权重和专家自带权重两者融合确定其最终权重，并以该权重修正原有证据，来增加各种证据的真实性。

1.1 冲突证据的识别

识别框架θ是用来判别某个有着两两互斥且有限结果的问题，它所有可能出现的结果用θ={θ1，θ2，…，θn}来表示。

定义1 在识别框架θ下，θ的所有子集能够形成一个2θ的新集合，则称m:2θ→[0，1]为基本信度分配函数，且满足

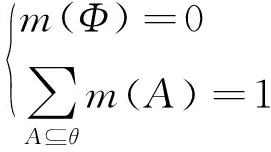
(1)

为了提高安全性分析中的精度和可靠性，可以将多源证据信息进行融合处理。在识别框架θ下，设存在两个证据E1、E2，相对应的基本信度分配为m1、m2，焦元为Bi、Cj，那么证据间的合成规则为

(2)

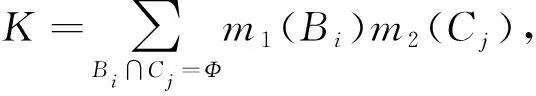
1.2 冲突证据的修正

针对高冲突证据之间不能直接进行融合的问题，目前很多研究学者都提出不同的改进方法[12，13]。文献[14]提出的以相似系数来辨别冲突程度的合成规则是一种既简单又有效的方法。它不仅阐述证据间相似度的计算方法，并且重新修正证据之间的权重，合理避免了冲突证据的完全否定，使其被有效应用。

定义2 在识别框架θ下，证据E1、E2相对应的基本信度分配函数分别为m1、m2，它们的焦元为Bi、Cj，则E1、E2之间的相似系数为

(3)

相似系数a12可以表明证据E1和E2间的相似性程度。a12∈[0，1]，若其值越接近1，则表明E1和E2越相似，它们之间的冲突性越小，当a12=1时，表示E1和E2完全一致；当a12=0时，E1和E2则完全冲突。

假设存在n个证据，利用公式(3)能够计算出它们中任意两个间的相似系数，将所有的系数列出构成了证据的相似系数矩阵

可知A是对称矩阵，把A中i行元素全部相加能得到所有证据对证据Ei的支持度为

(4)

将Z(mi)归一化处理后，能够得到Ei的可信度为

(5)

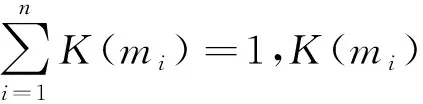
2 基于证据理论的TCC的TSR处理功能安全性评估

选取TCC的临时限速(Temporary speed restriction， TSR)处理功能为研究对象，建立基于证据理论和FMEA方法的安全性评估模型，采用FMEA识别系统潜在风险，从而可以确定评价对象的风险因素集[15]；然后结合相应的风险因子评分标准，每个专家对其风险因素的3个风险因子分别做出评价，利用证据理论来识别冲突证据，将证据之间的可信度权重和专家自带权重二者融合确定其最终权重，并以加权平均的方式对原有证据修正；最后由专家对风险因素的3个风险因子权重做出评价，再次修正后，可计算得到各个风险因素的RPN值，以排序的形式确定TCC的TSR处理功能的评估结果。

2.1 确定因素集

TCC的TSR处理功能的安全风险因素包括不能执行临时限速、错误执行临时限速、延迟执行临时限速、总是输出相同的临时限速命令、不能取消执行临时限速、错误取消临时限速、延迟取消临时限速、总是输出相同的取消临时限速命令等近8种风险因素集，表示为A={A1，A2，…，A8}。

2.2 确定风险因子的评估值

将TCC的TSR处理功能的风险分为极低、较低、中等、较高和极高5个评价等级，表示为B={R，L，M，H，VH}。各个风险因子O、S、D的评分标准见表1[16]。

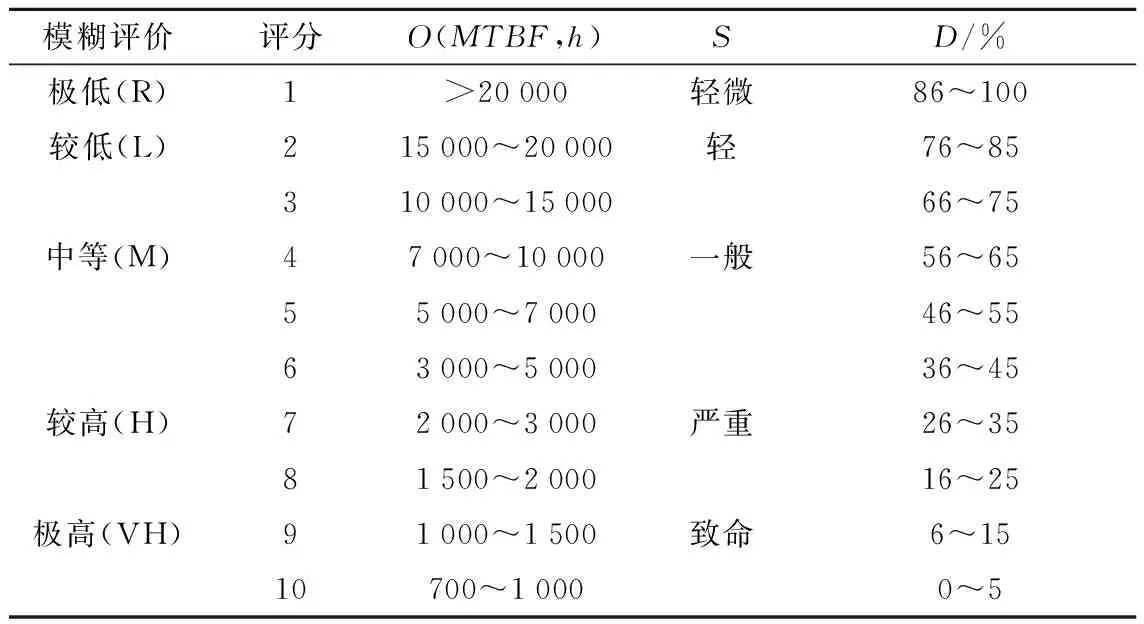
表1 风险因子的评分标准

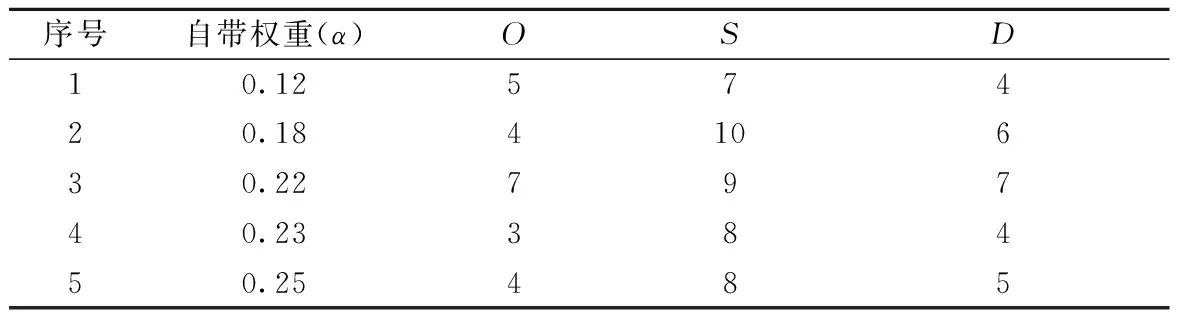
表2 A1中风险因子的初始评估值

将每一位专家评估结果做归一化处理后可以得出A1的风险因子评估mass函数，并依据公式(3)能得到证据间的相似矩阵为

按照公式(4)和公式(5)可得各个专家证据的可信度权重，依次为β=(0.199 8，0.200 3，0.199 0，0.199 6，0.201 3)。计算表明，大多数证据之间的可信度权重均在0.2周围浮动，证明其本身的一致性较好，故差距不明显。

设定证据之间的可信度权重和专家自带权重α二者等比例融合，利用式(2)可得到证据之间的最终权重为W=(0.119 9，0.180 3，0.218 8，0.229 5，0.251 5)。最后采用加权平均的方式对风险因子的初始评估值进行修正，得到TCC不能执行临时限速的3个风险因子的修正值，如表3所示。

表3 A1中风险因子的修正值

以A1不能执行临时限速O、S和D的评估值和修正值为数据基础，通过Matlab仿真能够将专家评价整体的变化趋势更直观地展现出来，如图2所示。

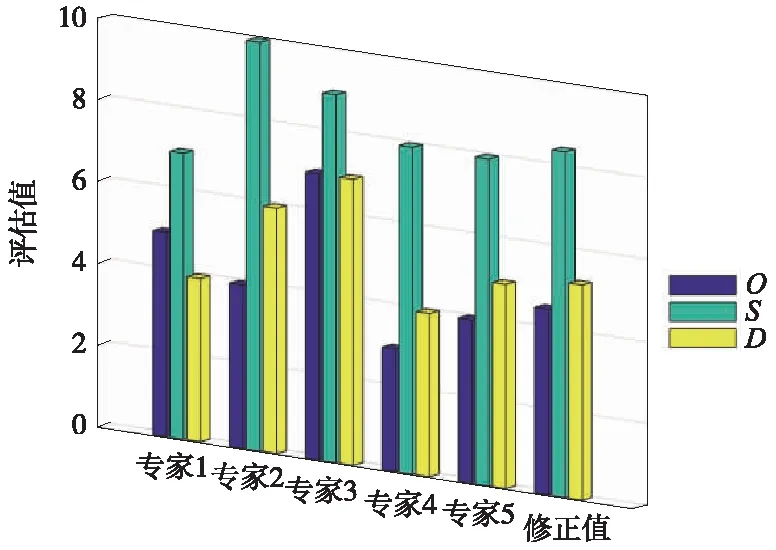
图2 专家评估值和修正值的变化趋势

按照类似方法可得到其余风险因素中各风险因子的修正值，如表4所示。

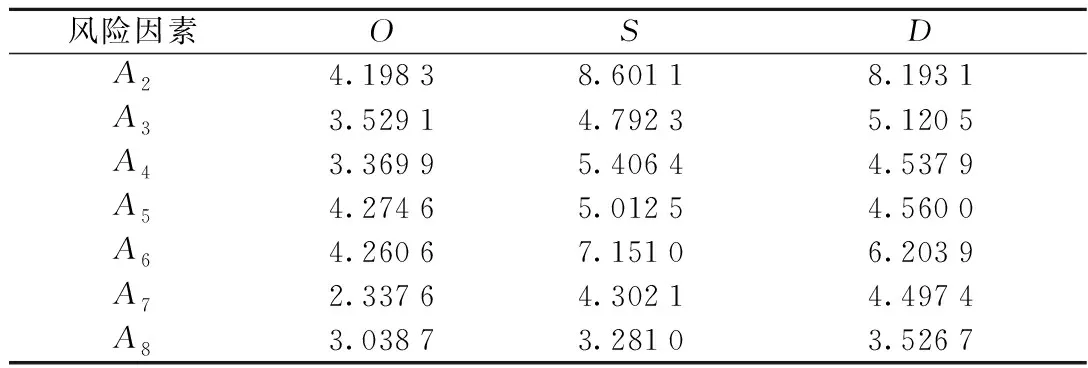
表4 其余风险因素中风险因子的修正值

2.3 确定风险因子的权重值

考虑到风险因子的权重也会影响TCC不能执行临时限速的安全性评估，由上述五位专家对其权重进行评估，结果见表5。

表5 风险因子权重的初始评估值

每位专家对于风险因子权重的评估结果本身都具有归一性，可直接利用公式(3)计算证据间的相似矩阵

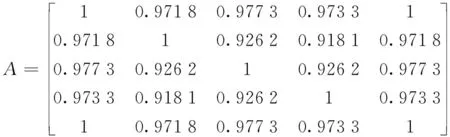
由公式(4)和公式(5)可得各个专家证据的可信度权重，依次为β=(0.203 1，0.197 6，0.198 4，0.197 7，0.203 2)。计算表明，大多数证据间一致性较好。

设定证据间的可信度权重和专家自带权重α二者等比例融合，利用式(2)可得到证据之间的最终权重为W=(0.122 0，0.178 0，0.218 4，0.227 5，0.254 1)。最后采用加权平均的方式对风险因子O、S、D权重的初始评估值进行修正，得到3个风险因子权重的修正值，分别为0.405 0、0.399 0、0.196 0。

以风险因子权重值对应修正各风险因素的评估值，可得到TCC的TSR处理功能所有风险因素的RPN值。同时以第一位专家的评估结果为例，采用传统方法计算各种风险因素的RPN值，对比结果见表6。

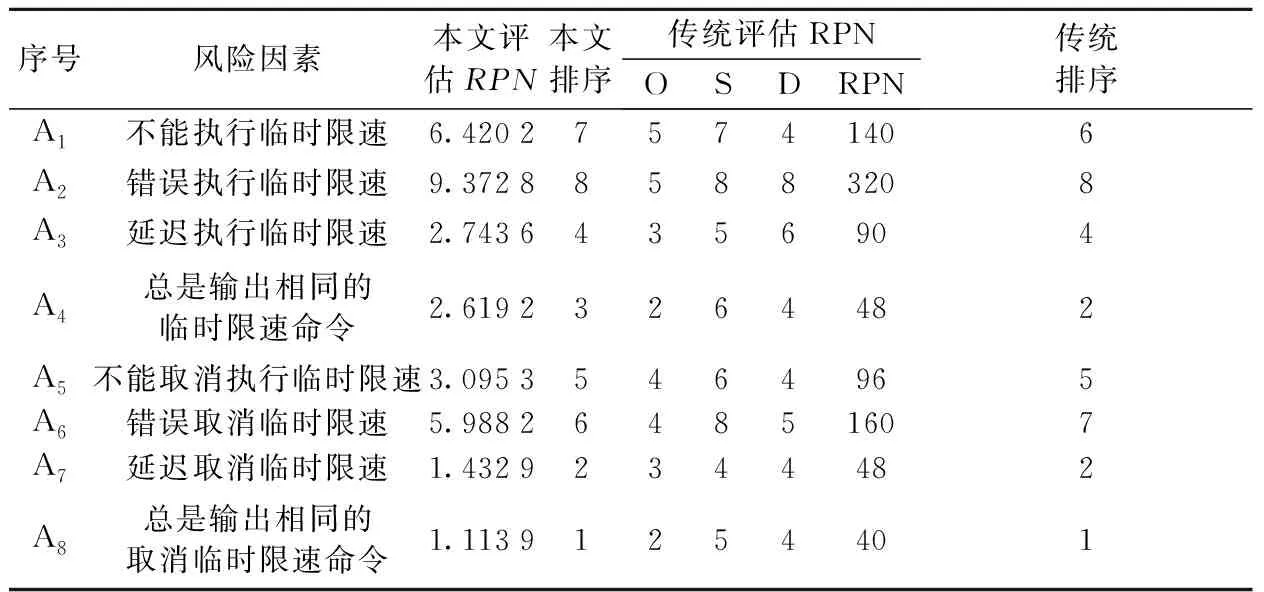
表6 TCC的TSR处理功能的安全性评估结果

由表6可见，对比传统方法，证据理论和FMEA相结合得到的评估结果更为精确。经与现场人员交流和统计故障数据，结果也基本符合现场实际情况。通过对TCC的TSR处理功能进行安全性评估，不仅解决了不同专家评分存在差异的特点，而且还考虑了FMEA 3个风险因子的权重，避免了不同的风险因素中O、S、D相乘得到相同的RPN值，如传统方法中总是输出相同的临时限速命令与延迟取消临时限速两个风险因素排序是一样的。可见本文方法无论是专家数据来源，还是风险因素的评估过程都是更为精确详细，更具有说服力。

3 结语

本文考虑到当前仍无法完全利用统计历史数据而需要借助专家数据进行评估的情况，提出了一种基于证据理论和FMEA相结合的评估方法。利用证据理论构建相似矩阵来识别冲突证据，将证据间的可信度权重和专家自带权重融合来确定其最终权重，并以该权重修正原有证据，解决了不同专家评分存在差异的问题。同时考虑了FMEA方法中风险因子权重的问题，提高评估过程的精确性，避免了不同风险因素的RPN值相同。本文通过实例分析验证了该方法的合理性和准确性，可以为今后TCC其他功能模块的安全性评估提供一定参考。

[1] 郜春海，燕飞，唐涛.轨道交通信号系统安全评估方法研究[J].中国安全科学学报，2005，15(10)：74-79.

[2] 张曙光.高速铁路系统生命周期安全评估体系的研究[J].铁道学报，2007，29(2)：20-26.

[3] Zhou G， Zhao H B， Quan H Y. Safety assessment of COTS RTOS based computer platform applied in train control system[C]//2013 IEEE International Conference on Intelligent Rail Transportation Proceedings. Beijing：2014.

[4] Medikonda B S， Ramaiah P S， Gokhale A A. FMEA and Fault Tree based Software Safety Analysis of a Railroad Crossing Critical System[J]. Global Journal of Computer Science and Technology， 2011，11(8)：56-62.

[5] An M， Chen Y， Baker C J. A fuzzy reasoning and fuzzy-analytical hierarchy process based approach to the process of railway risk information： A railway risk management system[J]. Information Science， 2011，181(18)：3946-3966.

[6] 徐征捷，张友鹏，苏宏升.基于云模型的模糊综合评判法在风险评估中的应用[J].安全与环境学报，2014，14(2)：69-72.

[7] 车玉龙，苏宏升.基于贝叶斯网络的列控系统安全风险评估方法[J].计算机工程与应用，2013，49(24)：238-242.

[8] Gargama H， Chaturvedi S K. Criticality Assessment Models for Failure Mode Effects and Criticality Analysis Using Fuzzy Logic[J]. IEEE Transactions on Reliability， 2011，60(1)：102-110.

[9] 徐琰珂，梁晓庚，贾晓洪.利用模糊证据理论的信息融合方法及其应用[J].哈尔滨工业大学学报，2012，44(3)：107-111.

[10] 罗贺，尹艳平，胡笑旋，等.基于可信因子的证据源修正方法[J].系统工程与电子技术，2015，37(6)：1459-1464.

[11] 张友鹏，李远远.基于云模型和证据理论的铁路信号系统风险评估[J].铁道学报，2016，38(1)：75-80.

[12] 费翔，周健.一种处理冲突证据的D-S证据权重计算方法[J].计算机工程，2016，42(2)：142-145.

[13] Wu Xiaoqian， Shen Yongjun， Zhang Guidong， et al. Information Security Risk Assessment Based on D-S Evidence Theory and Improved TOPSIS[C]∥Proceedings of 2016 IEEE 7th International Conference on Software Engineering and Service Science(ICSESS 2016). Beijing： 2016.

[14] 孙锐.基于D-S证据理论的信息融合及在可靠性数据处理中的应用研究[D].成都：电子科技大学，2012：32-38.

[15] 张友鹏，李远远，胡让.基于模糊证据理论的铁路信号系统风险评价[J].安全与环境学报，2017，17(1)：32-36.

[16] 马涛，米根锁，齐东.基于灰色理论ZPW2000A无绝缘轨道电路故障风险分析[J].铁道标准设计，2013，57(4)：115-118.