大跨公轨两用悬索桥动力特性的参数敏感性分析

张 兴,杜 斌,2,向天宇

(1.贵州大学,贵阳 550025； 2.贵州顺康路桥咨询有限公司,贵阳 550000； 3.西华大学, 成都 610039)

贵州省是一个多山深谷及喀斯特地貌广泛分布的省份，省内的城市轨道交通宜采用轻轨方案，虽然有轨电车基本上采用地面运行方式，但是在需要跨越沟谷河流的时候，仍需采用桥梁方案，这一问题在贵州的多山深谷地区会显得十分突出。同时，为了节省投资，缩短工期，还会在桥梁中采用有轨电车与市政道路共用交通线路的方式，即采用公轨两用桥梁[1-2]。随着我省经济水平的不断提高和建设水平增强，悬索桥以其独特的构造与技术特点，在跨越峡谷时展现出强大的竞争力，在省内得到广泛的应用。兴义市的马岭河三号特大桥为连接兴义市和义龙试验区的重要交通要道，跨径组成为(166+450+157) m，矢跨比为1/9，结构形式为地锚式单跨简支钢桁架公轨两用悬索桥，在跨中设柔性中央扣，如图1所示。该项目是公轨两用桥梁以及公轨两用悬索桥在贵州省内的首次应用。

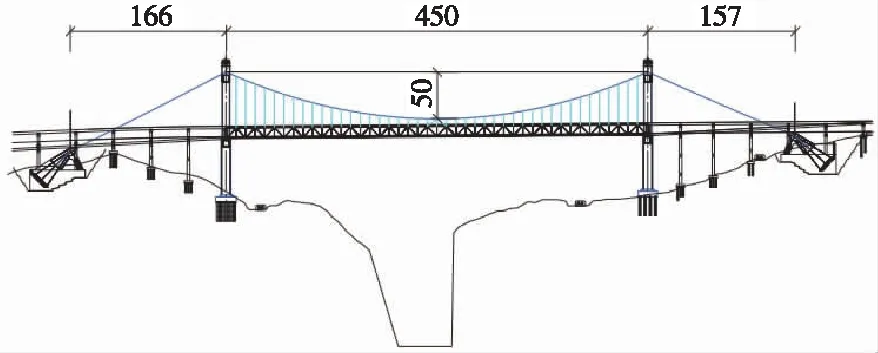
图1 马岭河三号特大桥立面布置(单位：m)

悬索桥属于柔性结构，非线性特征明显，这也决定了悬索桥相比普通桥梁结构具有独特的动力特性[3-6]。在大跨悬索桥动力特性方面，国内外学者开展了较多的研究：苏光亚等[2]采用三维有限元模型对某大跨公铁两用悬索桥的自振特性进行研究，得到了该悬索桥多向耦合振动的频率及振型；刘志翁等[7]采用子空间迭代法分析某单跨钢桁架悬索桥的自振特性，研究了加劲梁纵坡、散索鞍等参数的影响；徐良等[8]通过GPS现场实测和有限元模型对比了广州虎门悬索桥的自振动力特性，验证了大桥的抗震、抗风特征参数；王浩等[9]以润扬长江大桥为基础，采用子空间迭代法研究了刚性中央扣对大跨度悬索桥的动力特性的影响；徐勋等[10]以四渡河大桥为研究对象，研究了3种中央扣模型在动力激励下的动力特性；张宏斌等[11]采用脊梁骨式的有限元模型，探讨了自锚式悬索桥的动力特性并总结了影响自锚式悬索桥动力特性的因素；参数分析方面，肖勇刚等[12]研究了恒载集度、中央扣和结构刚度等参数对悬索桥成桥状态下动力特性的影响；丰硕等[13]探讨了恒载、加劲梁刚度、桥塔刚度等结构参数对自锚式混凝土悬索桥动力特性的影响规律。

到目前为止，虽然很多学者针对大跨度悬索桥动力特性做了大量工作，但是采用全桥离散单元模型系统性对大跨度公轨两用钢桁架地锚式悬索桥进行动力特性参数分析的研究较少。此外，相比普通的公路悬索桥，公轨两用悬索桥所受荷载大，荷载形式更为复杂，为了保证轨道交通的舒适性和安全性，对公轨两用悬索桥的动力特性进行掌握，是一项必不可少的研究内容之一，也是后期进行车桥耦合振动分析研究的前提[3]。本文以在建的马岭河三号桥为研究对象，采用Midas/Civil建立该桥的空间离散单元有限元模型，采用子空间迭代法，计算分析该桥的动力特性并分析各项结构参数变化对动力特性的影响。

1 有限元模型及动力特性分析

以马岭河三号桥为研究对象，跨径组成为(166+450+157) m，矢跨比为1/9，结构形式为半漂浮式单跨钢桁架地锚式悬索桥，桥塔为钢筋混凝土门式桥塔。采用Midas/Civil建立全桥成桥状态下的离散单元模型。如图2所示。其中主缆、吊杆采用只受拉的索单元模拟；主桁架单元采用空间梁单元模拟；主塔采用梁单元模拟。全桥共建立670个节点，各类单元共计1 658个。结构体系的约束条件为：忽略桩-土-结构相互作用的影响；塔底完全固结；主缆在塔顶主索鞍中心处固结；边跨主缆锚固于地锚上；主梁梁端在竖向、横桥向的自由度与桥塔横向相应节点采用主从约束。

图2 全桥模型

悬索桥作为柔性结构，应考虑恒载作用下重力刚度的影响；模态分析也较一般桥梁结构复杂。首先需要通过非线性迭代调整主缆和吊杆的初始单元内力，确定恒载作用下的成桥平衡状态；然后在此基础上，进行动力分析。基于Midas/Civil的特征值分析模块，采用考虑几何非线性的子空间迭代法，计算该桥前20阶自振模态和自振频率，结果如表1和图3所示。

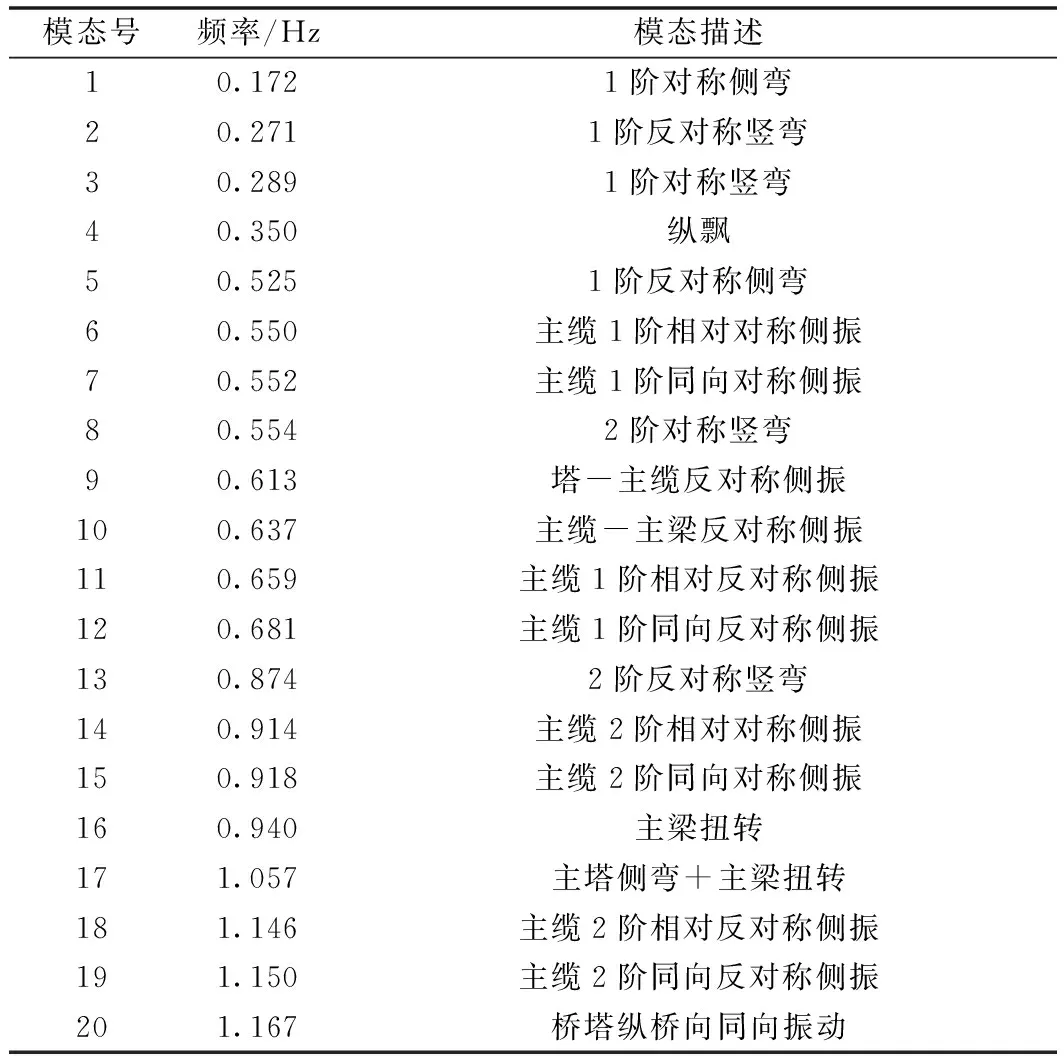
表1 前20阶自振频率及模态

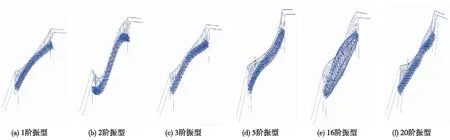
图3 主要代表性振型

从表1和图3可知，(1)马岭河三号桥的基频为0.172 Hz，振型为1阶对称横向侧弯，基频都在小频率范围内，这也印证了悬索桥为柔性结构的结构特点。因此在动力分析时，应考虑结构的几何非线性的影响。与文献[11]中1座跨径相当的公路悬索桥基频0.105 Hz相比，本桥的基频较高，说明公轨两用悬索桥相比公路悬索桥的结构刚度更大。(2)前20阶的振动模态，马岭河三号桥的振动模态主要有：主梁竖向弯曲、横向弯曲、主缆的侧向振动、主梁扭转、主塔侧振和纵向弯曲等几种形式。在低阶振型中，以主梁、主缆的振动为主，高阶振动中存在塔、主缆、主缆的耦合振动。(3)前20阶振型中，只出现2次侧向弯曲，以主缆和主梁的侧向振动出现较多，说明该桥的横向刚度较大，前20阶共出现4次竖弯，说明该桥的竖向刚度较小；只出现1次纵飘振型，且不是第1阶振型，说明该桥的纵向刚度较好；共出现2次主塔的振动，但是振型靠后，说明该桥的抗震性能较好。

2 结构参数对公轨两用悬索桥动力特性的影响

基于前述的有限元模型，对大跨度公轨两用悬索桥动力特性进行参数影响性分析。考虑的结构参数有：主塔刚度、主缆刚度、吊杆刚度、加劲梁刚度、恒载集度、中央扣和横向抗风支座等6类参数。采用控制变量法，改变某个参数的同时，保持其他参数不变，研究各结构参数对公轨两用悬索桥动力特性的影响。

2.1 主塔刚度对动力特性的影响

桥塔抗弯刚度分为纵桥向抗弯刚度和横桥向抗弯刚度。本研究通过改变桥塔整体抗弯刚度来分析桥塔刚度对悬索桥自振特性的影响。通过改变桥塔的纵桥向和横桥向的截面惯性矩I，来模拟桥塔刚度的变化。桥塔刚度的变化系数为0.5～2.0。图4为主塔刚度对动力特性的影响曲线。

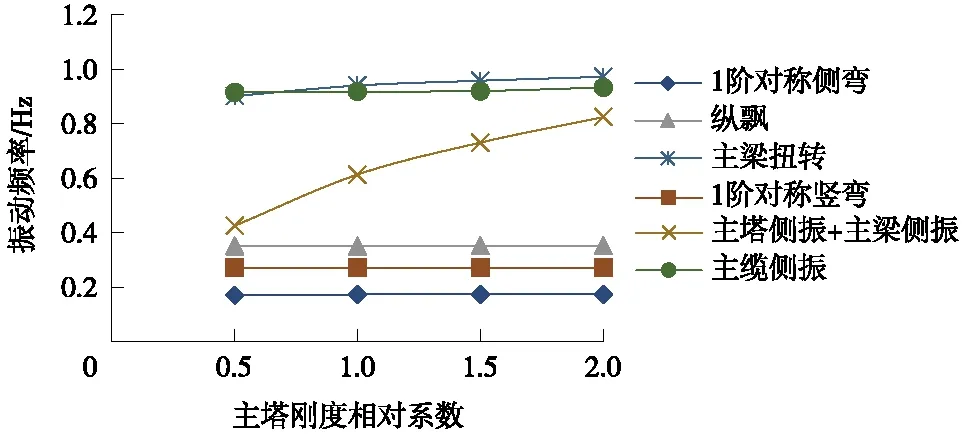
图4 主塔刚度对悬索桥动力特性的影响曲线

由图4可以看出，随着主塔刚度的增加，对以主塔振动为主的振型频率影响比较明显，当主塔刚度倍率从1.0提高到2.0时，主塔侧振频率提高34.5%。主塔刚度的改变，对悬索桥主梁的各方向的振动频率影响可以忽略不计。分析原因在于，本研究对象属于半漂浮体系，桥塔与主梁之间无直接连接，且联系较弱，因此主塔刚度的变化，对主梁振动频率的影响甚微。

2.2 主缆刚度对动力特性的影响

主缆的刚度主要由材料的弹性模量与主缆面积来确定。考虑改变主缆面积，会间接造成主缆恒载的变化，引入新的变化因素。这对于定量分析来说，难以准确判定被控制的变量的影响程度。因此，在此考虑材料弹性模量E的变化，所引起刚度变化，同时也可模拟主缆材料变化所带来的刚度变化。主缆刚度相对系数取0.5～2.0。图5为主缆刚度对悬索桥动力特性的影响曲线。

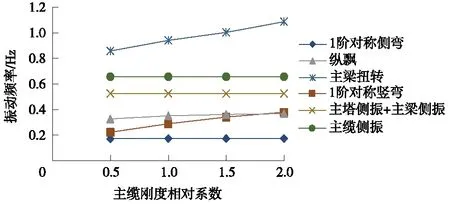
图5 主缆刚度对悬索桥动力特性的影响曲线

从图5中可以看出，随着主缆刚度的增加，对以主梁振动为主的主梁扭转、主梁1阶竖向振动频率影响较明显。当主缆刚度系数从1.0提高到2.0时，主梁扭转频率提高15.5%，主梁1阶竖向振动频率提高27.2%。主缆刚度的增加对于主缆侧振、主梁侧振等振型的频率影响甚微。

2.3 吊杆刚度对动力特性的影响

吊杆的刚度与主缆刚度相似，是由材料的弹性模量与吊杆面积来确定。考虑吊杆面积较小，增加面积，不会引起过大的额外恒载。因此，这部分的研究采用改变吊杆面积A，模拟吊杆刚度的改变。吊杆刚度相对系数取0.5～2.0。图6是吊杆刚度对悬索桥动力特性的影响曲线。

图6 吊杆刚度对悬索桥动力特性的影响曲线

从图6可以看出，随着吊杆刚度的增加，对结构顺桥向振动频率影响较大；对于悬索桥纵飘频率，随着吊杆刚度系数从1.0增加到2.0，纵飘频率提高约20.0%。桥塔顺桥向振动受吊杆刚度的影响，但影响甚微。桥结构在横桥向和竖向振型，对吊杆刚度的变化不敏感，基本不受吊杆刚度变化的影响。

2.4 加劲梁刚度对动力特性的影响

加劲梁刚度由加劲梁截面的抗弯惯性矩I和弹性模量E决定。加劲梁刚度分为横向刚度和竖向刚度，本次研究，采用改变加劲梁整体刚度的办法来研究加劲梁刚度变化对动力特性的影响。由于研究对象的加劲梁为钢桁架，不宜采用改变弦杆的抗弯惯性矩的办法来改变加劲梁刚度，因此考虑通过调整腹杆高度H来模拟加劲梁的刚度变化。腹杆高度变化取值为(0.8～1.25)H，对应加劲梁刚度相对系数0.5～2.0。由于加劲梁恒载大，因腹杆高度改变引起的恒载变化，可忽略不计。图7为加劲梁刚度对悬索桥动力特性的影响曲线。

由图7可以看出，随着加劲梁刚度的改变，对主梁侧弯和主梁扭转振型频率的影响显著。当加劲梁刚度系数从1.0提高到2.0时，主梁1阶侧弯频率提高33.3%，主梁扭转频率提高23.2%，因此，提高加劲梁刚度，有助于提高结构的横向刚度和改善结构的颤振性能。加劲梁刚度的提高，对1阶对称竖弯频率影响较小，当加劲梁刚度系数从1.0提高到2.0时，主梁1阶竖弯频率提高约10.0%，这也证明了对于大跨悬索桥结构，重力刚度对竖向刚度的贡献最大，加劲梁刚度对竖向刚度的影响甚小。

图7 加劲梁刚度对悬索桥动力特性的影响曲线

2.5 恒载集度对动力特性的影响

在上文中，模拟构件刚度改变时，均最大程度地避免了引入恒载变化造成悬索桥结构动力特性的影响。在这一部分，采用改变加劲梁荷载、桥面荷载倍率的办法，研究恒载集度对悬索桥结构动力特性的影响。恒载相对系数取0.5～2.0。图8为恒载集度对动力特性的影响曲线。

从图8可以看出，恒载集度的变化，对结构自振频率的影响较大；随着恒载集度的增加，以主梁振动为主的侧弯、竖弯、扭转振型的自振频率均有不同程度的降低。当恒载集度相对系数从1.0提升到1.5时，主梁1阶侧弯、1阶竖弯及扭转基频分别降低21.2%，19.8%和15.5%。分析原因，随着恒载集度的增加，结构的重力刚度得到提升，同时也使结构的振动质量增加，但是恒载集度对后者的贡献更大，2种因素共同作用，最终导致以主梁振动为主的振型频率降低。因此增加恒载集度，在一定程度上会降低悬索桥结构的整体振动频率。

图8 恒载集度对悬索桥动力特性的影响曲线

2.6 中央扣对动力特性的影响

中央扣的主要作用是提高悬索桥的整体刚度[14]，中央扣分为柔性中央扣和刚性中央扣。本研究的对象在设计时，设置了柔性中央扣。为了探究中央扣的类型对公轨两用悬索桥动力特性的影响，本研究采用的3种计算模型，对比分析中央扣对悬索桥动力特性的影响。柔性中央扣的模拟根据设计文件，采用吊杆单元模拟；刚性中央扣则采用刚性连接模拟。计算结果如表2所示。表2按无中央扣模型的前10阶振型进行排序，其余两种模型的振型按照模态描述对应到相应的位置。

表2 3种中央扣形式下的频率和振型

由表2可以看出，无中央扣模型与有中央扣模型相比，前10阶振型的振动模态基本相同，但是相同的振动模态所对应的振动频率和出现的时机不同。变化最为明显的是纵飘振型，根据频率大小排序，无中央扣模型的1阶振型为纵飘，而有中央扣模型的纵飘振型出现在第4阶，并且随着中央扣刚度的提升，纵飘振型的阶次逐渐向后推移。这说明了设置中央扣对于悬索桥的纵向刚度有较大提高。对比柔性中央扣模型和刚性中央扣模型的振型，前三阶振型均为1阶对称侧弯、1阶反对称竖弯、1阶对称竖弯，随着中央扣刚度的变化，主缆的1阶侧向振动频率提高，主缆-主梁的反对称侧向振动频率提高。与柔性中央扣模型不同的是，在刚性中央扣模型中，主缆1阶相对反对称侧振会在前10阶振型中出现。总的来说，中央扣的刚度对悬索桥结构的侧向振动频率影响比较明显。

2.7 横向抗风支座对动力特性的影响

横向抗风支座的主要作用是在横风荷载作用下，对加劲梁进行有效的横向限位，有利于行车舒适性和悬索桥结构的安全性[15]。为了探究横向抗风支座对悬索桥结构动力特性的影响，建立2种有限元模型，对比设置抗风支座和不设抗风支座2种模型的动力特性。计算结果如表3所示。

从表3可以看出，在前10阶振型中，设有抗风支座的模型的振动模态以加劲梁竖弯和主缆侧振为主，说明主梁的横向刚度较高。对于不设抗风支座的模型，前10阶振型以加劲梁横飘和主缆侧振为主，说明取消横向抗风支座，解除了悬索桥结构的横向限位，结构易发生横桥向的振动。因此横向抗风支座，对于提高结构抵抗横向荷载的能力有积极的作用；从振动频率来看，不设横向抗风支座的模型的前10阶振型中，相同振型的频率，均小于设有横向抗风支座的模型，说明设有横向抗风支座的悬索桥结构，结构的整体刚度比较高。

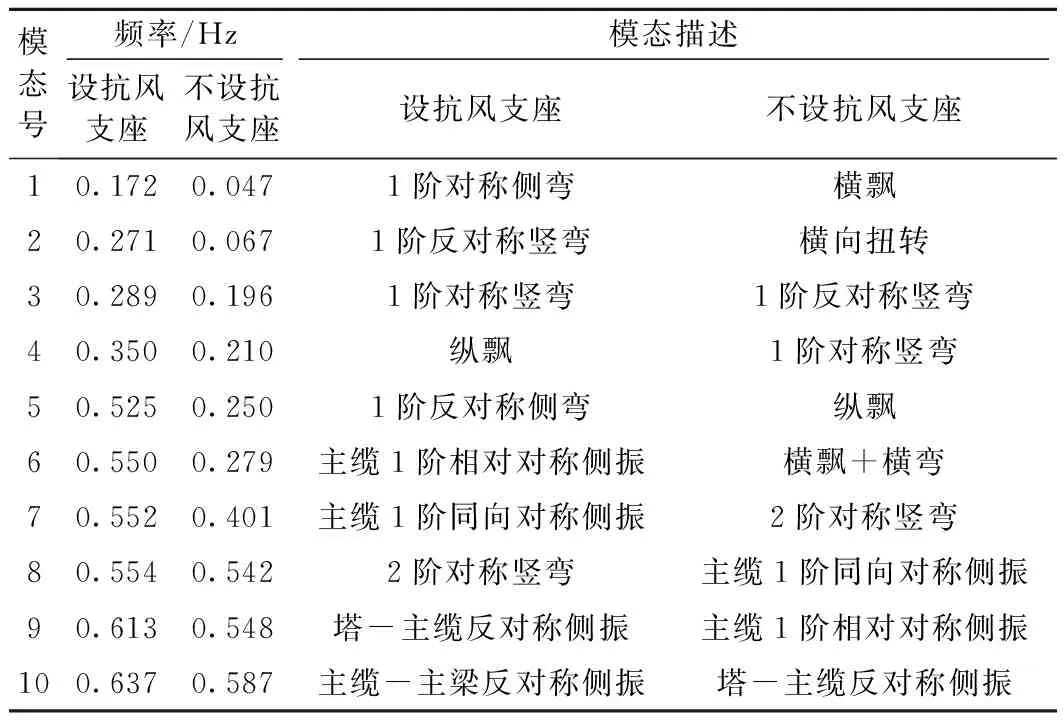
表3 抗风支座对振动频率和振型的影响

3 结论

本研究以大跨度公轨两用钢桁架悬索桥为研究对象，利用大型通用有限元软件Midas/Civil，建立空间离散单元有限元模型，采用子空间迭代法，得到该桥的动力特性，并分析不同参数变化对大跨度公轨两用钢桁架悬索桥自振特性的影响，最终得出以下结论。

(1)马岭河三号桥模型的基频为0.172 Hz，对应的1阶振型为横向对称侧弯，属于小频率范围，动力分析时，应按照柔性结构进行分析。与跨径类似的公路悬索桥相比，结构的整体刚度较同等跨径的公路悬索桥更高。

(2)索塔刚度、主缆刚度、吊杆刚度及恒载集度的变化，对1阶振型的影响较小。中央扣对1阶振型的频率影响较大。是否设置中央扣和抗风支座会导致1阶振型发生变化。

(3)随着桥塔刚度增加，以桥塔振动为主的振型频率明显提高；随着主缆刚度提高，主缆竖向振动和主梁扭转的频率提高较显著；随着吊杆刚度的增加，除纵飘频率提高以外，其余振型无显著变化；随着加劲梁刚度提高，主梁侧弯和主梁扭转振型频率的提高显著。

(4)随着恒载集度的增加，以主梁振动为主的侧弯、竖弯、扭转振型的自振频率均有不同程度的降低。这是重力刚度和振动质量同时增加共同作用的结果。

(5)设置中央扣和横向抗风支座能有效增加结构整体刚度。

[1] 李永乐，董世赋，臧瑜，等.大跨度公轨两用悬索桥风-车-桥耦合振动及抗风行车准则研究[J].工程力学，2012，29(12)：114-120.

[2] 陈东巨.大跨度公轨两用单跨悬索桥研究[J].铁道标准设计，2017，61(5)：70-76.

[3] 苏光亚，高日，陈丽莹，等.公铁两用悬索桥自振特性分析[J].铁道工程学报，2002，19(3)：43-47.

[4] 陈仁福.大跨悬索桥理论[M].成都：西南交通大学出版社，2015.

[5] Feng M. Modern bridges in China[J]. Structure & Infrastructure Engineering， 2014，10(4)：429-442.

[6] Choi D H， Gwon S G， Yoo H， et al. Nonlinear static analysis of continuous multi-span suspension bridges[J]. International Journal of Steel Structures， 2013，13(1)：103-115.

[7] 刘志翁，刘世忠，武维宏.钢桁式加劲梁悬索桥动力特性分析[J].兰州交通大学学报，2010，29(4)：95-101.

[8] 徐良，江见鲸，过静珺.广州虎门悬索桥的模态分析[J].土木工程学报，2002，35(1)：25-37.

[9] 王浩，李爱群，杨玉冬，等.中央扣对大跨悬索桥动力特性的影响[J].中国公路学报，2006，19(6):49-53.

[10] 徐勋，强士中.中央扣对大跨悬索桥动力特性和地震响应的影响研究[J].铁道学报，2010，32(4)：84-91.

[11] 张宏斌，孔宪京，张哲.自锚式悬索桥动力特性分析[J].公路交通科技，2004，21(7)：66-69.

[12] 肖勇刚，陈伟华.大跨度悬索桥动力特性的参数分析[J].长沙理工大学学报(自然科学版)，2016，13(1)：28-33.

[13] 丰硕，项贻强，谢旭，等.自锚式悬索桥动力特性及结构参数影响规律研究[J].世界桥梁，2004(4)：50-53.

[14] 徐勋，强士中，贺拴海.中央扣对大跨悬索桥动力特性和汽车车列激励响应的影响[J].中国公路学报，2008，21(6)：57-63.

[15] 李剑，丁啸宇，郭彬立.苏拉马都大桥主桥抗风支座与抗震挡块协同受力分析[J].公路，2011(1)：100-105.