基于粒子群优化的UKF在SINS/GPS组合导航中的应用

徐晓苏，闫琳宇 ，吴晓飞 ，庞 东，彭源源

（1. 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 东南大学 仪器科学与工程学院，南京 210096；3. 天津航海仪器研究所，天津 300131）

捷联式惯性导航系统（Strapdown Inertial Navigation System, SINS）具有自主性强、隐蔽性好、信息全面等优点，在航空、航天、航海和许多民用领域中得到了广泛应用，成为目前各种航行体上广泛使用的一种主要导航设备[1]。但是其误差随时间积累，仅靠捷联式惯性导航系统很难完成高精度、长航时的导航任务。为减少捷联式惯性导航系统的累计误差，采用误差不随时间积累的 GPS导航系统提供的数据作为外部信息，对捷联式惯性导航系统误差进行校正[2]。卡尔曼滤波器是实现组合导航系统的核心，对于非线性系统来说，因为它要处理无穷维积分运算，要得到精确地最优滤波解是很困难的，为此人们提出了大量次优的近似非线性滤波方法，利用非线性卡尔曼滤波器解决组合导航非线性误差模型的状态估计问题。目前扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）是两类比较常用的非线性Kalman滤波器[3]。其中无迹Kalman滤波的计算复杂度与扩展Kalman滤波同阶次，但其实现较简单，不需要解析的微分计算，因此采用无迹卡尔曼滤波器用于本组合导航系统[4]。

应用卡尔曼滤波器进行数据融合需要对系统噪声协方差矩阵和测量噪声协方差矩阵进行设置：前者影响卡尔曼滤波算法的滤波性能及参数估计精度；后者取值不当会影响滤波器的修正速度，使滤波过程不稳定甚至发散[5]。由于SINS系统中陀螺仪和加表的白噪声强度是随机的，系统中观测噪声也未知，所以在很多实际系统中，系统过程噪声方差矩阵和观测噪声方差矩阵事先是未知的或不确切的。在以往的实验中这两个参数一般由实验人员反复试验或者依据前人给出的经验值进行设定，这个过程耗费实验人员的时间和精力且不能保证参数最优。

粒子群（Particle Swarm Optimization, PSO）优化算法是模拟鸟群捕食行为过程中通过集体协作，寻求群体最优解的全局优化算法。PSO算法结构简单但具有处理并优化复杂问题的能力，广泛应用于参数优化、信号处理等实际问题中[6]。

本文利用粒子群算法对卡尔曼滤波器的未知的或不确切的滤波参数和进行寻优，将得到的优化值作为卡尔曼滤波器的输入参数来优化卡尔曼滤波器的噪声矩阵，改善了因为不准确的噪声统计增加导航模型不确定性而引起的卡尔曼滤波器状态估计效果差、组合导航精度低的问题。

1 SINS/GPS松组合导航滤波器模型设计

SINS/GPS 组合导航系统由SINS 分系统、GPS分系统和组合导航滤波器三部分组成。采用误差不随时间积累的GPS导航系统提供的数据作为外部信息，对捷联式惯性导航系统误差进行校正，可以减少捷联式惯性导航系统的累计误差，提高导航精度和性能。根据数据融合和组合深度的不同，SINS/GPS 组合导航系统可分为松组合、紧组合和深组合三种模式。其中SINS/GPS松组合是一种低水平的位置/速度组合方式[7]，此种模式易于实现，其状态方程和量测方程如下面所述。

1）状态方程

SINS主要误差状态包括姿态误差角、速度误差、位置误差以及惯性器件误差，选取如下15个量构成15维状态向量：姿态误差速度误差位置误差系下的加速度计常值误差以及陀螺常值误差

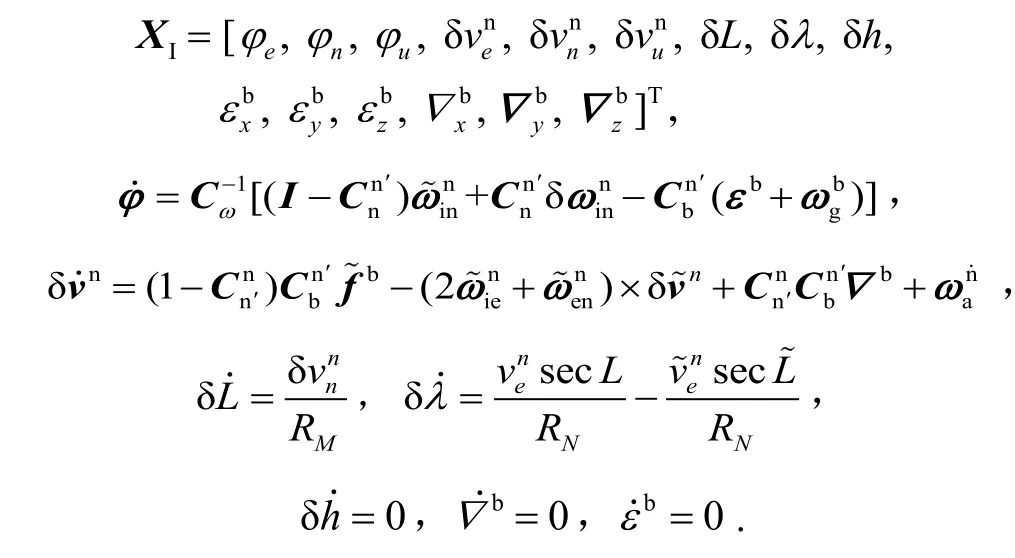
式中：为陀螺仪白噪声，中白噪声，两者均为对角元素相等的三阶对角矩阵。

以采样周期T作为滤波周期，可以使用四阶龙格库塔积分方法，以T为步长将其离散化，离散后的状态滤波方程为：

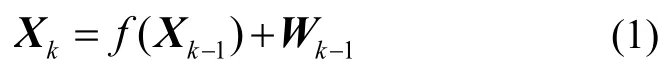
式中，为系统噪声协方差矩阵，可表示为

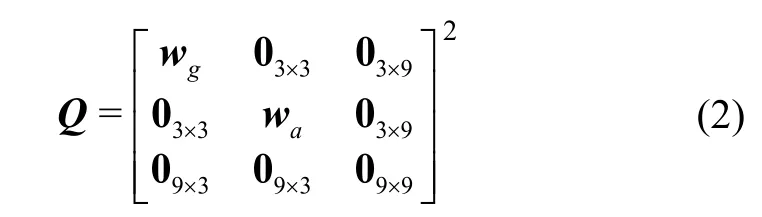
2）量测方程

松组合量测矢量取SINS和GPS地理坐标系下的位置、速度量测信息。

将位置量测方程和速度量测方程合并后得：

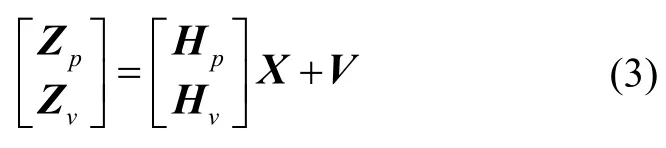
其中：

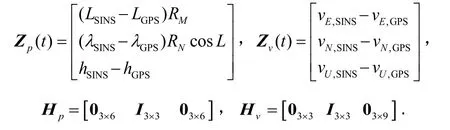
同样离散化后可记为为观测方程随机噪声，为观测噪声协方差矩阵，可表示为

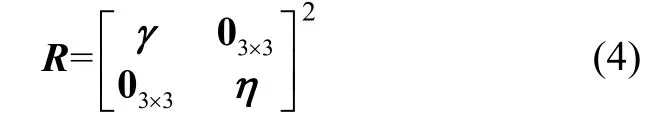
其中，分别为位置和速度观测噪声误差矩阵，均为对角元素相等的三阶对角阵。

2 无迹卡尔曼滤波

由第1节可知，SINS/GPS 组合导航系统中状态方程为非线性问题，需要利用非线性Kalman滤波器。扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）和粒子滤波（PF）是三类比较常用的非线性滤波器。粒子滤波不依赖任何局部的线性化技术和非线性函数逼近法，但代价是计算量大[8]。扩展Kalman滤波、无迹Kalman滤波是基于逼近方法的滤波器。其中无迹Kalman滤波的实现较简单，不需要解析的微分计算，该方法在处理状态方程时首先利用UT变换得到一组sigma采样点，然后利用变换后的状态变量进行滤波估计，经过非线性函数映射得到随机变量的均值和方差，避免了线性化误差，具有较高的估计精度[9]。因此采用无迹卡尔曼滤波器用于本组合导航系统。

考虑如下非线性模型：

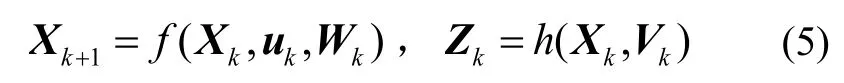
式中：为系统状态；维向量函数为n维系统随机噪声，为系统噪声协方差矩阵；维观测方程随机噪声，为观测噪声协方差矩阵。

无迹卡尔曼滤波计算过程如下：

步骤1初始化：

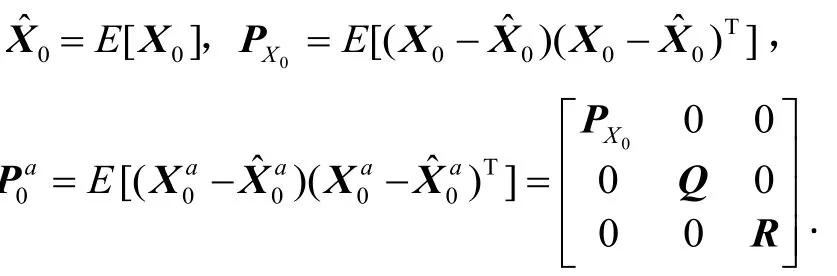
式中：为系统的增广状态变量；为过程噪声和观测噪声的协方差矩阵。

步骤2计算Sigma点

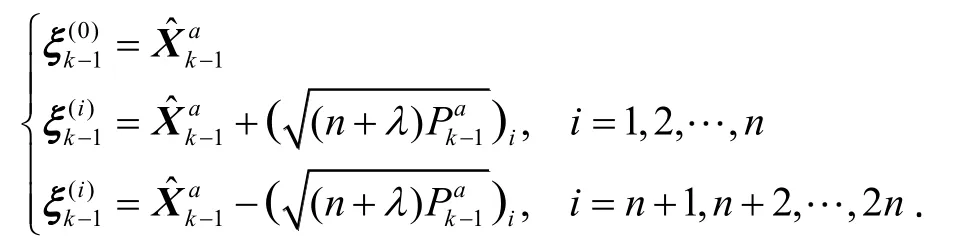
步骤 3计算时间更新方程，通过状态方程的传播计算Sigma点

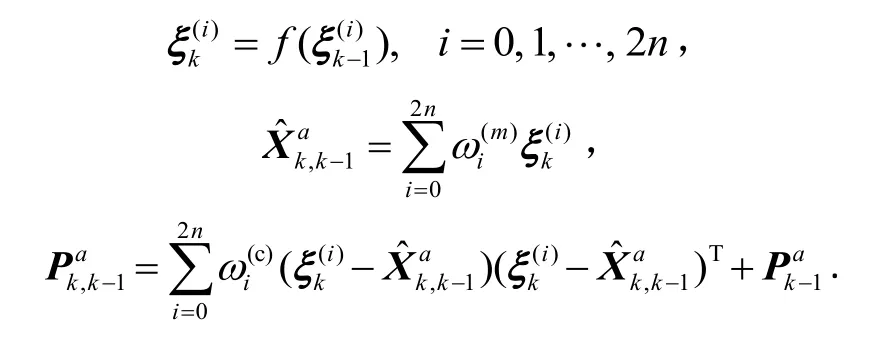
步骤4计算观测更新方程：

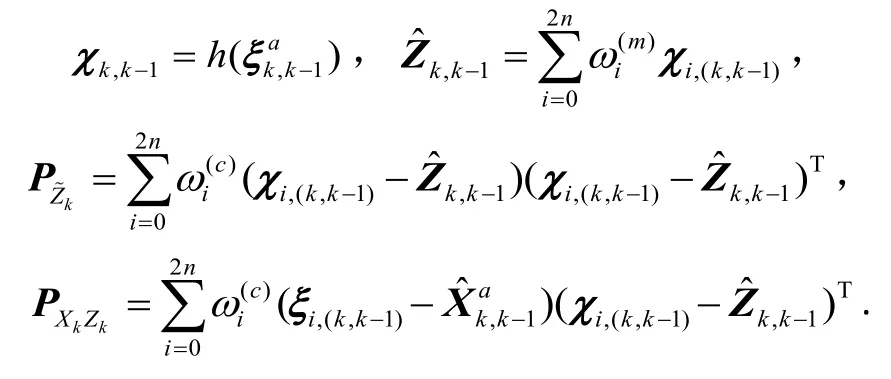
步骤5滤波更新：

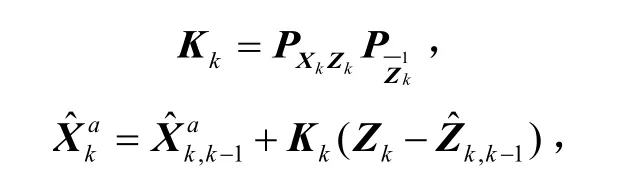
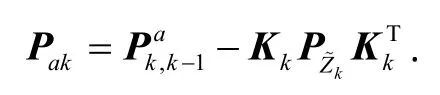
其中，参数计算公式为：

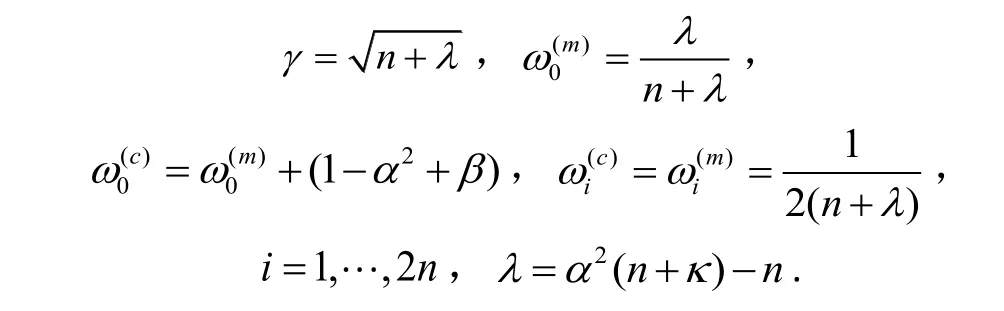
式中：为一个复合刻度参数；n为增广状态向量维数；为决定先验均值附近Sigma点分布广度的主要刻度因素，的典型范围为是强调验后协方差计算的零阶Sigma点权值的第二刻度因素（β可以根据已知时刻的先验随机变量来最小化特定的高阶误差项，对于高斯先验分布的情形，β=2为最优）；为第三刻度因素，通常取为

3 粒子群算法优化的UKF

3.1 粒子群算法的基本原理

粒子群优化算法是模拟生物群体进化过程中通过集体协作，寻求群体最优解的全局优化算法。每个粒子通过不断地学习更新，按照一定规律向个体最优值和全局最优值加速运动，最终输出全局最优解。可以利用它对参数进行随机搜索得到全局最优参数，其具体步骤如下：

步骤1初始化粒子群的参数，在参数区间内初始化粒子群的位置和速度，随机产生若干粒子并初始化最优粒子；

步骤2设置适应度函数，对每一个粒子的适应度进行评价，比较其与最优粒子的适应度值，若适应度更好则取代最优粒子；

步骤3粒子迭代更新自己的速度和位置，每个粒子（维解空间的一个候选解）根据自身和群体经验调整轨迹向最优点靠拢，按以下方程式进行更新[10]：

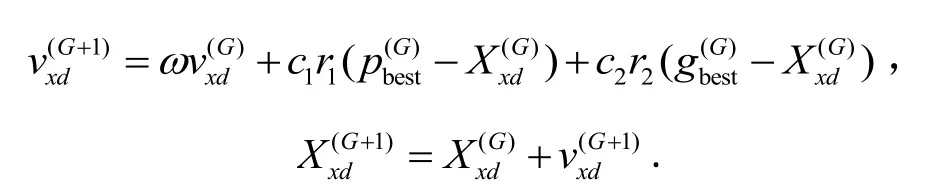
式中：G为迭代次数，分别为粒子x在第G代的位置和速度，为粒子x第G代为止搜索到的最好位置，为整个粒子群G代为止搜索到的最好位置，为惯性权重，为学习因子，为0～1之间的随机数。

步骤4重复步骤2和步骤3，更新最优粒子，直至满足迭代次数或精度要求，产生最优粒子及其适应度值。

3.2 粒子群算法对UKF的优化

由粒子群算法原理可知，粒子和合适的适应度函数是粒子群算法的关键。无迹卡尔曼滤波器中和取值不当会增大系统的不确定性，使滤波过程不稳定，这两个参数的选取对于组合导航系统的性能有着关键影响。由前述SINS/GPS松组合导航滤波器模型可知：为15×15的方阵，且对角元素只包含为6×6方阵，对角元素为因此在对无迹卡尔曼滤波器的优化中，将无迹卡尔曼滤波器的滤波参数和作为粒子，即对四个数值进行寻优。而SINS/GPS组合导航系统性能主要取决于位置精度，所以将滤波器输出的位置误差的均方差作为适应度函数：

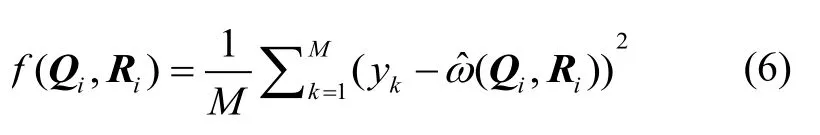
式中：

Qi、Ri为无迹卡尔曼滤波器的噪声参数；为参数时组合导航系统位置误差的均方差；为估计的位置值；为估计长度；为参考的实际位置值。

显然，适应度函数值越小，即位置误差的均方差越小，相应的参数粒子就越优。按照上述粒子群算法的步骤对初始化粒子群和进行寻优，最后将结果作为滤波器的输入参数来优化卡尔曼滤波器的噪声协方差矩阵。具体流程图如图1所示。

PSO优化SINS/GPS组合导航系统中UKF噪声协方差矩阵参数的结构图如图2所示。

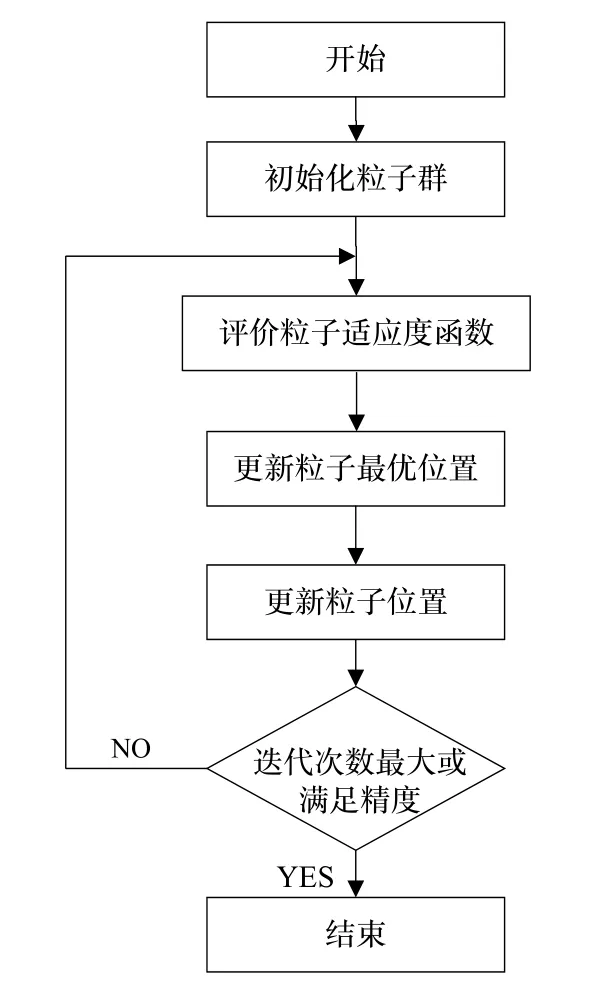
图1 PSO优化粒子流程图Fig.1 Flow chart of particle swarm optimization

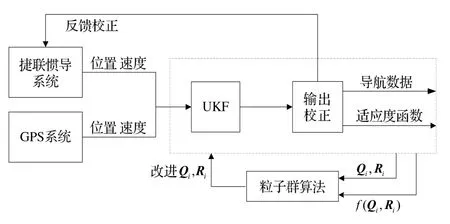
图2 PSO优化组合导航UKF参数的结构图Fig.2 Structure chart of UKF parameters based on PSO in SINS/GPS integrated navigation system

4 实验结果与分析

4.1 仿真实验

仿真过程中，通过比较最终的导航误差来验证不同滤波参数下的组合导航性能。利用轨迹发生器产生汽车运行轨迹，利用SINS模拟器产生SINS测量数据。具体的仿真条件为：汽车初始位置为东经118°，北纬32°，运动过程时间为3 600 s；陀螺仪的常值漂移为0.2 (°)/h，白噪声均方差为0.02 (°)/h；加速度计的常值零偏为100 μg，白噪声均方差为100 μg；SINS系统的输出频率为100 Hz，GPS系统的输出频率为10 Hz，组合系统的数据输出频率为100 Hz。卡尔曼滤波器的参数值由粒子群优化算法得到。

在粒子群优化算法的参数设置中，根据文献[11]，设定初始化粒子个数取20，预定迭代次数为10。将随机产生的第一代粒子作为初始化最优粒子值，通过粒子群算法对Q、R进行寻优，将实验重复进行12次，观测并比较每一次的全局最优粒子值，仿真实验结果如图3所示。通过计算实验结果，12次实验中粒子群算法搜索出的参数均值分别为0.020 8 (°)/h、94.782 7 μg，非常接近设置噪声参数值及标准参数值0.02 (°)/h、100 μg。

由图3还可以看出，每次寻优结果差异不大，通过试验得出的参数用于组合导航系统实验的系统性能也非常接近。参数均值用于本组合导航仿真实验的结果如图4。通过仿真实验验证了粒子群算法能够有效地搜索出滤波参数的最优值。

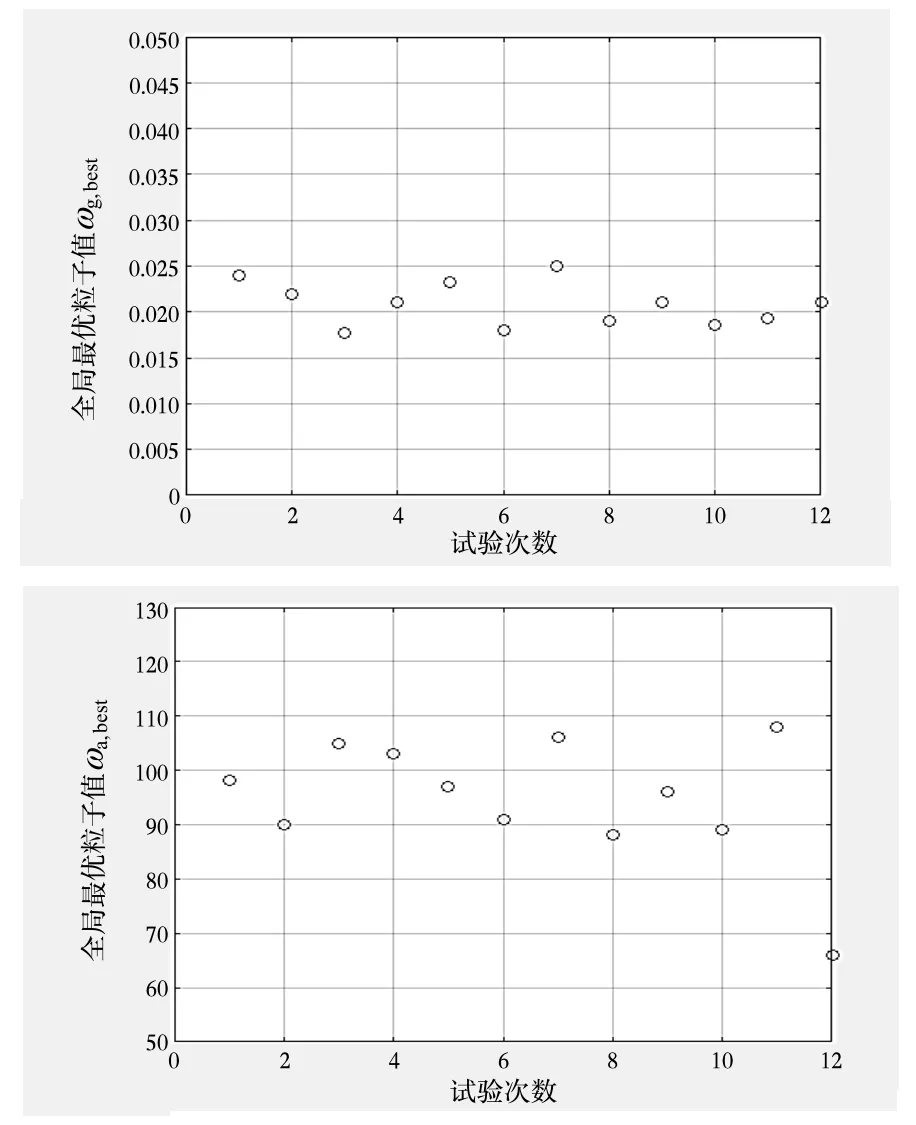
图3 12次实验产生的最优滤波参数Fig.3 The best filtering parameters in 12 experiments

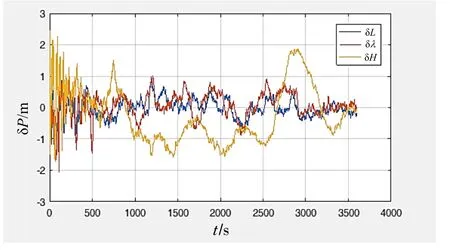
图4 PSO寻优参数均值用于GPS/SINS组合导航实验的位置误差Fig.4 Position errors of SINS/GPS system based on PSO

4.2 半物理实验

采用实验室车载实验的数据进行仿真，实验数据在南京采集。初始位置为东经118.787 613°，北纬32.059 484°，高度10.23 m；初始速度为0 m/s；初始姿态为纵摇角为-1.65°，横摇角为1.36°，方位角为88.91°。实验采用的捷联惯导系统包括三个光纤陀螺仪和三个石英加速度计。实验还采用了诺瓦泰公司生产的FlexPark6 GNSS接收器。参考导航数据由法国公司 IXBLUE生产的PHINS和FlexPark6 GNSS接收器的松组合模式提供。PHINS和IMU放在同一个底座上。GNSS的东北天速度误差均为0.1 m/s，位置误差优于1 m，采样频率为1 Hz。SINS解算中，陀螺仪常值漂移小于0.01 (°)/h，随机白噪声强度小于0.01 (°)/h；加速度计常值漂移为±50 μg，白噪声强度小于50 μg。数据总时间为3600 s，更新频率200 Hz。跑车位置、速度、姿态曲线分别如图5～7所示。

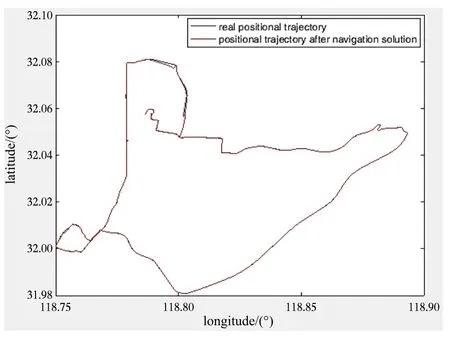
图5 跑车轨迹与解算轨迹Fig.5 Vehicle trajectory & calculated trajectory

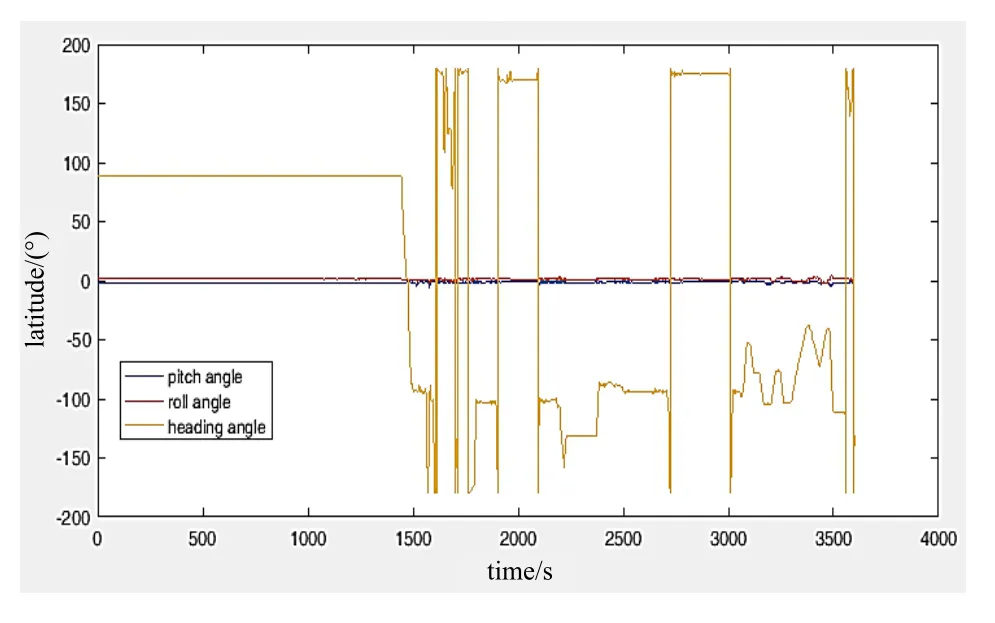
图6 跑车姿态角Fig.6 Attitude angles of the vehicle

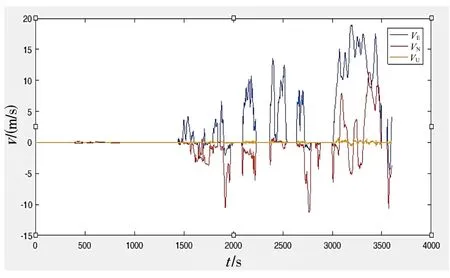
图7 跑车速度Fig.7 Velocities of the vehicle

在粒子群优化算法的参数设置中，初始化粒子个数取20，预定迭代次数为20，仍根据文献[11]设定将离子群算大随机产生的第一代粒子作为最优粒子值通过粒子群算法对Q、R进行寻优，将寻优后的噪声协方差矩阵参数值与根据经验值设定的参数值得出的位置误差曲线图进行对比，最终得出的位置误差曲线如图8～10所示。

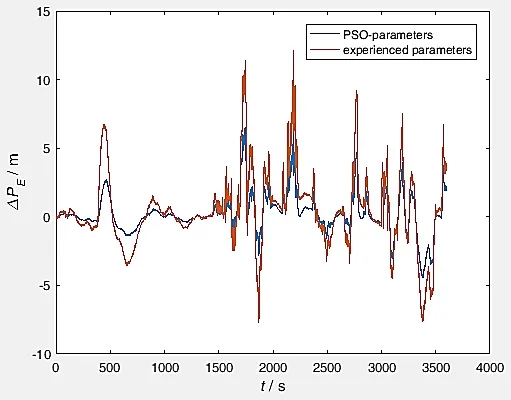
图8 东向位置误差对比Fig.8 Comparison on eastern position errors

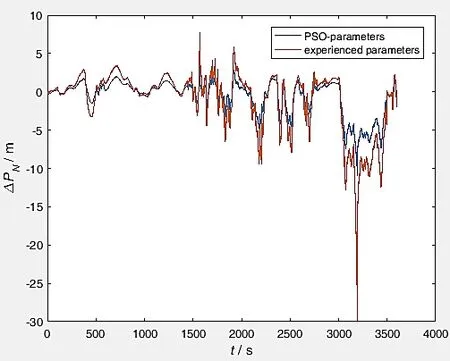
图9 北向位置误差对比Fig.9 Comparison on northern position errors

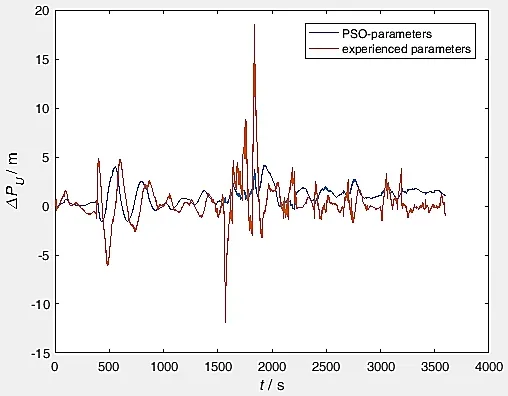
图10 天向位置误差对比Fig.10 Comparison on up position errors

由图8～10可知，经过粒子群算法优化噪声协方差矩阵的UKF应用于SINS/GPS组合导航系统中，其位置误差在整个实验时间内整体有减少的效果，尤其在各个位置误差峰值处优化效果显著。

比较PSO优化参数前后SINS/GPS松组合导航系统输出的姿态误差、速度误差、位置误差的均值和均方差，如表1所示。

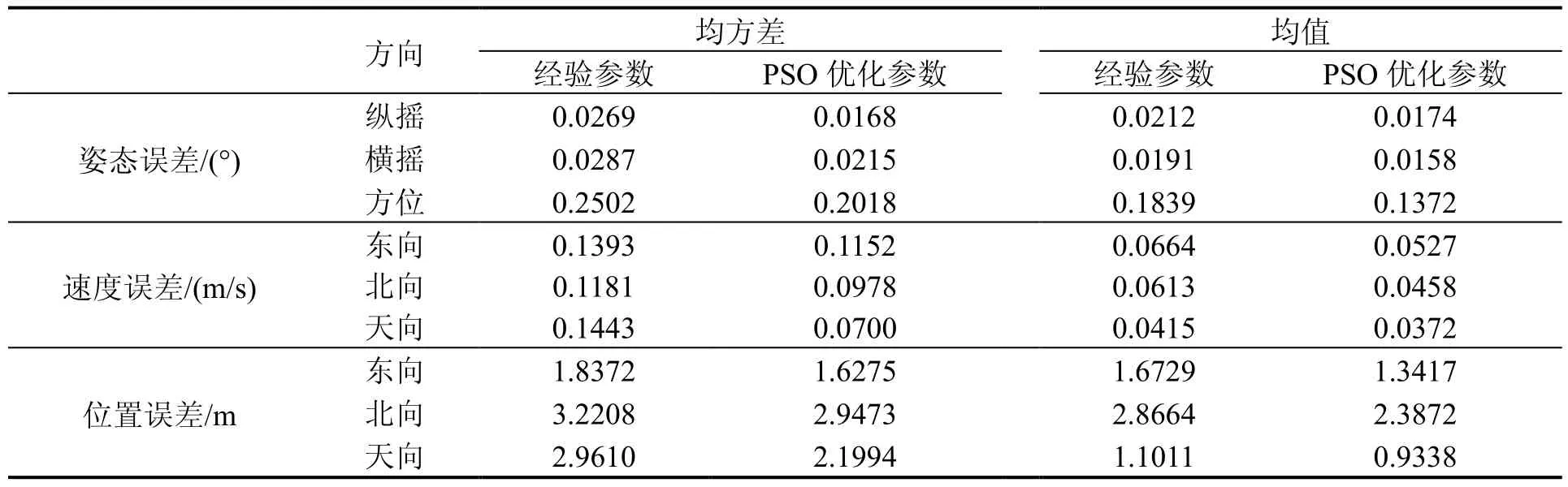
表1 姿态误差、速度误差、位置误差的均方差和均值Tab.1 Mean variances and mean values of errors of attitude, velocity, and position

由表1可知，经过粒子群算法优化后的UKF用于组合导航系统与经验参数设定下UKF的系统相比，位置误差的均值和均方差均有15%～30%的降低。实验结果说明经过粒子群算法优化参数的 UKF能够更好地抑制噪声，提高SINS/GPS松组合导航系统的精度。

5 结 论

SINS/GPS组合导航系统噪声协方差矩阵和测量噪声协方差矩阵参数的选取会影响系统的性能。在一般的实验中，这些参数是依据前人经验或者反复试验设置得到的，参数的确定过程需要耗费实验人员大量的时间和精力。本文提出的粒子群算法优化组合导航系统噪声协方差矩阵的方法能够根据目标函数的适应值直接搜索出最优参数，提高UKF抑制噪声的性能，从而提高SINS/GPS组合导航系统的性能。实验结果表明：粒子群算法能够搜索出组合导航系统噪声协方差矩阵参数的最优值，将它应用到组合导航系统中是可行的。

参考文献（References）：

[1] 徐晓苏, 周峰, 张涛, 等. 遗传算法优化的神经网络在SINS/GPS中的应用[J]. 中国惯性技术学报, 2015,23(3): 322-327.Xu X S, Zhou F, Zhang T, et al. Application of neural network by genetic algorithm optimization in SINS/GPS [J].Journal of Chinese Inertial Technology, 2015, 23(3): 322-327.

[2] Yao Y Q, Xu X S, Zhu C C. A hybrid algorithm for GPS/INS integration during GPS outages[J]. Measurement,2017, 103: 42-51.

[3] Fakoorian S, Azimi V, Moonsavi M, et al. Ground reaction force estimation in prosthetic legs with nonlinear Kalman filtering methods[J]. Journal of Dynamic Systems Measurement and Control, 2017, 139(11): 111004(1-11).

[4] Xu X, Xu X S, Zhang T, et al. A Kalman filter for SINS self-alignment based on vector observation[J]. Sensors,2017, 17(2): 264-282.

[5] 张旭辉, 林海军, 刘明珠. 基于蚁群粒子群优化的卡尔曼滤波算法模型参数辨识[J]. 电力系统自动化, 2014,38(4): 44-50.

Zhang X H, Lin H J, Liu M Z. Parameter identification of Kalman filter algorithm model based on ant colony particle swarm optimization[J]. Automation of Electric Power Systems, 2014, 38(4): 44-50.

[6] Langeveld J, Engelbrecht A P. Set-based particle swarm optimization applied to the multidimensional knapsack problem[J]. Swarm Intelligence, 2012, 6(4): 297-342.

[7] 王君帅, 王新龙. SINS/GPS紧组合与松组合导航系统性能仿真分析[J]. 航空兵器, 2013(2): 14-19.

Wang J S，Wang X L. Simulation and analysis of SINS/GPS tightly coupled and loosely coupled integrated navigation system[J]. Aero Weaponry, 2013(2): 14-19.

[8] Dehghan N E, Farhidzadeh A, Salamone S. Nonlinear Kalman filtering for acoustic emission source localization in anisotropic panels[J]. Ultrasonics, 2014, 54(2): 486-501.

[9] Jin X B. UKF fusion estimation for indoor RFID tracking[J]. Applied Mechanics and Materials, 2013, 427-429: 582-585.

[10] Liu J, Shi T Y, Li P, et al. Trajectories planning for multiple UAVs by the cooperative and competitive PSO algorithm[C]//IEEE Intelligent Vehicles Symposium. 2015: 107-114.

[11] 刘志雄, 梁华. 粒子群算法中随机数参数的设置与实验分析[J]. 控制理论与应用, 2010, 27(11): 1489-1496.

Liu Z X, Liang H. Parameter setting and experimental analysis of the random number in particle swarm optimization algorithm[J]. Control Theory & Applications, 2010,27(11): 1489-1496.