三频差分GNSS/INS紧组合模型

肖 凯，孙付平，王浩源

（解放军战略支援部队信息工程大学，郑州 450001）

导航与位置服务是当今信息时代的重要需求。目前，世界几大卫星导航系统播发的信号有美国GPS的L1CA/L2C/L5、俄罗斯 GLONASS的 G1C/G2C/L3、中国北斗卫星导航系统（BeiDou Navigation System,BDS）的B1/B2/B3，以及欧盟GALILEO的E1/E5a/E5b/E6。其中，我国北斗卫星导航系统率先全星座提供三频信号服务。未来，随着几大卫星导航系统的建设和发展，越来越多的在轨卫星将提供三频乃至多频信号，用户更能利用多系统的多个频点带来的优势[1]。可见，研究和利用多频信号是发展趋势。三频信号最显著的贡献是提供了额外频点的载波相位观测量，可用于快速、准确地解算整周模糊度[2]。Forssell最早提出了三频模糊度解算算法(Three-carrier Ambiguity Resolution, TCAR)[3]，Jung也随后提出了CIR（Cascaded Integer Resolution）算法[4]。TCAR和CIR虽然细节不同，但基本原理一致，后来学者针对多频提出的模糊度解算算法也是遵循其逐级取整固定的思路。TCAR/CIR算法最早是针对GPS未来多频信号的前瞻性研究，目前我国学者已对其应用并改进，来解算北斗三频模糊度[5-7]。关于三频模糊度解算的研究正日趋成熟，但对于 GNSS/INS组合导航，还没有开展如何利用三频信号的研究。

GNSS/INS组合导航系统主要有松组合、紧组合、深组合三种模式[8]。应用最广泛的是差分载波相位紧组合[9-10]，能在短基线下通过站间星间作差，得到不含卫星轨道误差、大气延迟误差、接收机钟差等误差的高精度载波相位观测值，从而实现厘米级定位精度。对于三频信号，紧组合因能直接使用原始观测值，更能充分获取第三频点信号带来的优势。因此，有必要研究三频信号对GNSS/INS紧组合的贡献。可以预见的是，基于三频信号的TCAR算法速度快，可以减少组合导航的解算时间。另一方面，TCAR算法不稳定的问题也有望通过INS辅助得到改善。

根据三频信号和紧组合的特点，基于TCAR算法，构建了三频差分GNSS/INS紧组合模型。首先阐述了模型的设计思路；然后给出了观测模型和模糊度解算方法，并分析了新模型和经典模型的不同处；最后使用车载组合导航实验数据对新模型进行了验证。

1 模型的结构设计

BDS/INS紧组合模型采用扩展Kalman滤波算法进行BDS和INS系统间的数据融合处理。

基于差分载波相位的GNSS/INS紧组合，其关键是求模糊度整数解，否则只能得到浮点解结果，不能精密定位。对模糊度的处理，经典模型采用附加模糊度参数的形式，将模糊度也作为状态参数之一，与导航误差、惯性元件误差一起在Kalman滤波器中估计，得到模糊度浮点解及其协方差阵，再使用最小二乘降相关法( Least-squares Ambiguity Decorrelation Adjustment, LAMBDA )得到模糊度整数解[11]。LAMBDA 算法由Teunissen在1995年提出，通过对模糊度浮点解和协方差阵进行整数变换，再进行序贯最小二乘求解，最终得到模糊度整数解[12]。在三频信号体制下，模糊度参数的个数显著增加，如果延用经典模型的方法，将使 Kalman滤波器阶数上升，运算复杂度增加，并且在卫星信号中断时，如果不能及时解算出模糊度参数，Kalman滤波器容易发散[13]。此外，如果使用LAMBDA算法，额外频点信号也会增加搜索时间。因此，模糊度的处理值得仔细考虑，既要避免额外频点信号带来的负担，也要使处理方法与紧组合模型相契合。综上分析，建立了三频差分GNSS/INS紧组合模型（后文简称三频模型），其结构如图1所示。

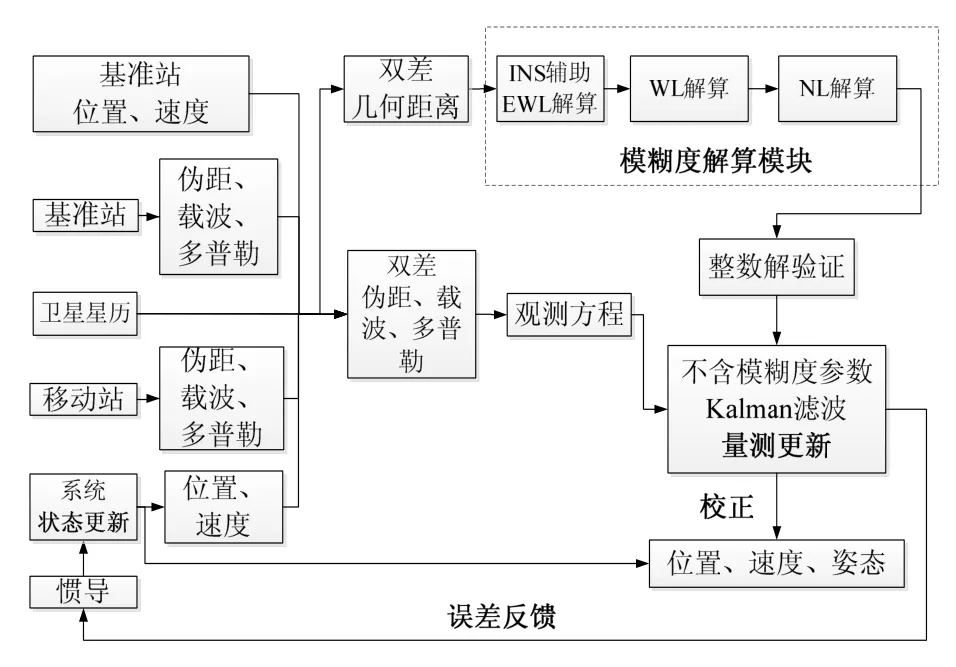
图1 三频差分GNSS/INS紧组合模型的结构Fig.1 Architecture of triple-frequency differential GNSS/INS tightly coupled integration model

2 系统模型

在组合导航中，需要关心的参数是其中，r表示位置，v表示速度，ψ表示姿态，ba和bg分别表示加速度计和陀螺的零偏。对于高精度惯导，可忽略标度因子误差和交叉耦合误差。此外，本文将ba和bg建模为常值。因为Kalman滤波器经过线性化处理，滤波时处理的状态参数实际是x的误差于是系统状态方程可表示为：

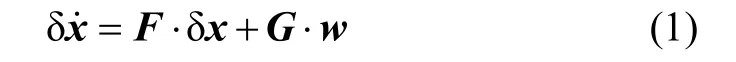
式中：δx表示状态参数向量；F表示状态转移矩阵；w是系统的噪声向量；G是噪声投影矩阵。

式(1)的详细表达式由 INS系统和所选择的坐标系决定。本文采用效率较高的地心地固坐标系，并用方向余弦矩阵表征载体姿态，则惯性导航误差方程可表示为：

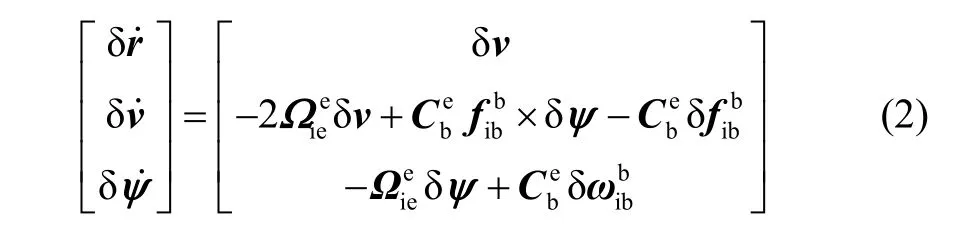
其中：表示由载体b系到地心地固e系的方向余弦矩阵；表示加速度计比力输出；表示陀螺角速率输出；δψ表示姿态失准角误差；表示由地球自转角速率构造的斜对称阵。于是可根据式(2)得出式(1)的详细表达式[14]，在此不再详述。

3 观测模型

GNSS载波相位观测方程为：

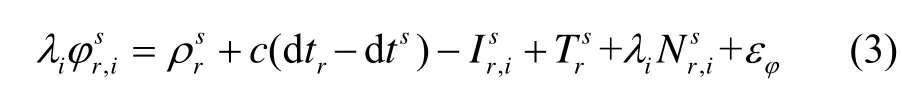
式中：r和s表示该量与接收机或卫星相关；i表示频点；λi表示载波波长；表示载波相位观测值；表示卫星和接收机的几何距离；c表示光速；dtr和dts表示接收机钟差和卫星钟差；表示电离层延迟和对流层延迟；表示整周模糊度；εφ表示载波测量噪声。在短基线下，通过作双差可以消除大气层延迟误差、卫星钟差、接收机钟差。去掉上下标r和s，双差载波相位观测方程表示为：

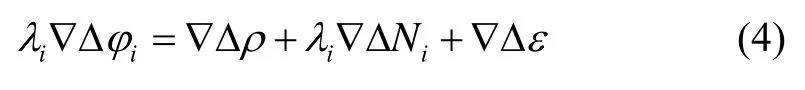
式中，ε∇Δ表示双差残余误差。

使用北斗系统B1、B2、B3频点的载波相位φ1、φ2、φ3，可以构造组合观测量如式(5)所示。其波长λ(i,j,k)和整周模糊度如式(6)(7)所示。

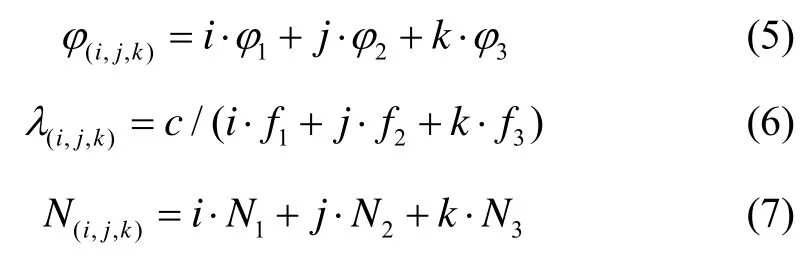
式中：c表示光速；f表示频率；下标数字表示频点；(i,j,k)表明是组合量，i、j、k为对应于B1、B2、B3频点的组合系数。

由惯导解算可以得到接收机预测位置INSr ，从而计算卫星和接收机的双差几何距离∇ΔρINS。用∇ΔρINS替换式(4)中的双差伪距∇Δρ，并将式(4)写成组合观测量的形式，可得：

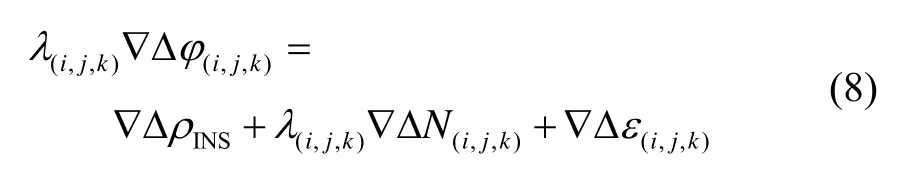
于是，可参照TCAR算法的步骤，依次解算超宽巷 EWL（Extra Wide Lane）、宽巷 WL（Wide Lane）、窄巷NL（Narrow Lane）的模糊度。TCAR一般采用无几何模型，直接取整得到模糊度整数解。与LAMBDA算法相比较，该算法模型简单，运算速度更快，且各颗卫星的模糊度独立解算，相互间没有影响[15]。由于不需要模糊度浮点解及其协方差阵，也使得 TCAR算法解算模糊度的过程可以独立于 Kalman滤波的量测更新。

首先，根据式(8)的原理，使用式(9)计算 EWL。式(9)中，[ ]是取整算子。

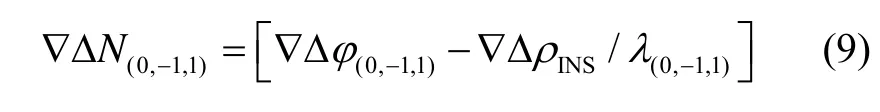
原始的 TCAR算法使用 B3频点的双差伪距计算EWL，但在观测条件和北斗系统误差的影响下，伪距容易出现粗差，令EWL的解算不可靠。本文使用INS预测几何距离，取代B3频点伪距，辅助TCAR算法。显然，若令式(9)取整正确，要满足：

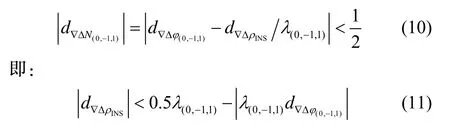
式中，d表示该量的误差。不考虑其它因素的影响，设BDS单频载波噪声标准差为典型值 0.002 m[16]，则双差载波噪声标准差为0.004 m，按照99.70%的置信区间取三倍标准差，即0.012 m。根据组合量误差传递公式[17]，得到EWL的载波噪声放大因子为28.5287。最后得EWL的双差载波噪声代入式(11)得：

由于基准站无位置误差，则：

式中：分别表示移动站接收机到参考星p和选择星q的1×3方向余弦矢量；表示位置误差。假设并且惯性预测位置三个方向误差相等，则有：

所以，若要保证惯性辅助TCAR算法可行，所采用的 IMU要满足滤波周期内单方向位置误差积累小于1.21 m。

根据式(9)得到的 EWL模糊度计算EWL的载波相位等效距离值：

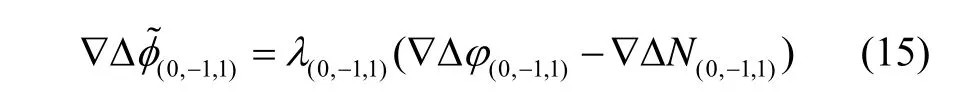
使用式(15)得到的计算两个WL模糊度：

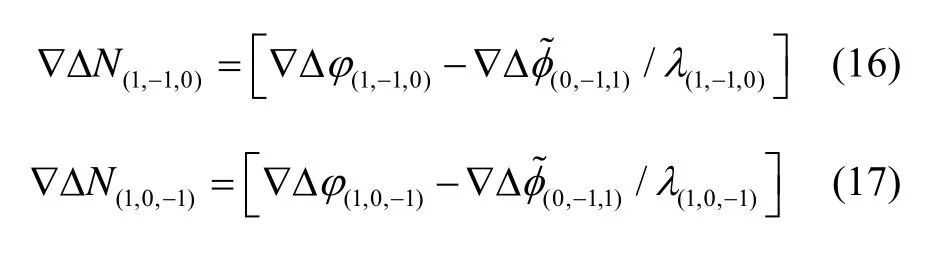
使用式(16)得到的WL模糊度计算WL的载波相位等效距离值：

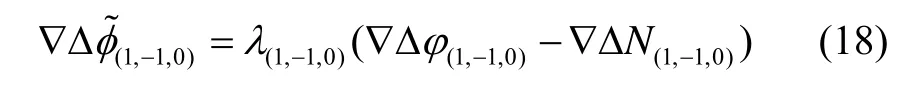
最后，使用式(16)～(18)，得到NL模糊度：

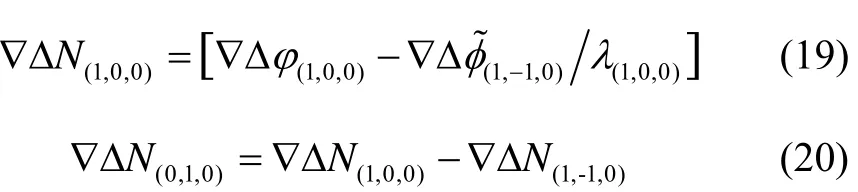
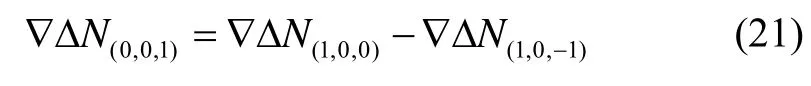
NL模糊度即为各频点的模糊度整数解。将其代入Kalman滤波的观测方程，观测方程表示为：

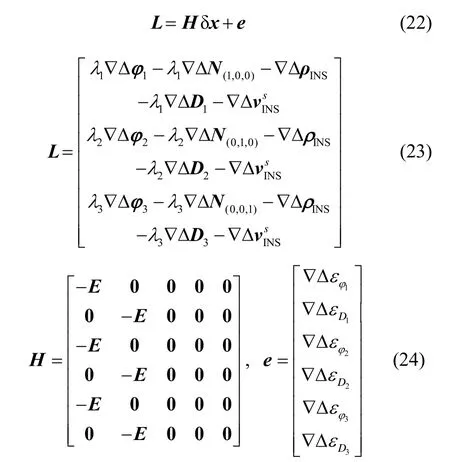
式中：E是接收机到卫星的方向余弦构成的 1×3矩阵；D是多普勒观测值；是用惯导预测速度计算的接收机和卫星的相对速度；ε表示各观测量的观测噪声。

如上得到了系统模型和观测模型，之后便可按照Kalman滤波算式进行状态更新和量测更新。

结合图1和观测模型可知，三频模型与经典模型的不同之处是：

① 在模糊度解算部分，使用 INS辅助的 TCAR算法，而不是LAMBDA算法。

② 模糊度的解算独立于量测更新，避免了附加模糊度参数带来的滤波阶数上升，并且不需要计算模糊度浮点解。

③ 不使用移动站的伪距观测量。这是因为不需要构建伪距观测方程来辅助计算模糊度浮点解，并且TCAR算法利用惯导提供的位置计算几何距离，也不需要构建双差伪距观测量。

②和③是新模型的优点。

4 实 验

为验证三频模型的有效性，并对比三频模型与经典模型的解算时间消耗和精度，在郑州市高新区进行了车载组合导航实验。跑车时长约52 min，首尾各有约9 min静止段。移动站与基准站距离保持在7.6 km左右，可视北斗卫星数保持在9颗。惯导设备是星网宇达公司某型光纤惯导，标称陀螺零偏 1 (°)/h，加速度计零偏0.5 mg，采样率100 Hz。GNSS接收机采用司南三星八频测量型接收机，采样率1 Hz。卫星天线与IMU之间的杠杆臂用全站仪精确测量，误差在厘米级。设备安装和跑车轨迹见图2。

图2 设备和跑车轨迹Fig.2 The equipment and vehicle trajectory

4.1 解算时间消耗

完整的组合导航解算主要由状态更新、量测更新（求模糊度浮点解和状态参数）、模糊度解算三个部分组成。用Qt框架（https://www.qt.io/）和C++语言编写程序，分别使用经典模型和三频模型进行组合导航计算，记录各部分的时间消耗。去掉首尾的静止段，统计的历元总数为2008。表1是卫星数为9颗时的时间消耗。通过设置参与计算的卫星数，模拟可视卫星数不同时的情况，得到卫星数4～9颗时对应的时间消耗，如图3所示。需要补充说明的是：①状态更新部分的时间消耗均相同，为21000 ms左右；②在模糊度解算部分，不管卫星数多少，TCAR算法时间消耗极短，单历元不足1 ms，计算机无法计时，而LAMBDA算法随卫星数不同，时间消耗在10 635～19 304 ms之间；③总时间除了包含量测更新和模糊度解算，还包含卫星位置计算、差分观测量计算、INS预测几何距离计算、周跳探测等部分，因为三频模型和经典模型的这些部分基本一样，时间消耗差别小，也不是关注点，故没有在表1中列出。

由表1可知，在可视卫星数为9颗时：

① 三频模型的量测更新时间仅有经典模型的16.7%；三频模型的模糊度解算部分时间消耗极短，而经典模型需要19 304 ms。这表明，三频模型在量测更新和模糊度解算部分具有显著的优势。

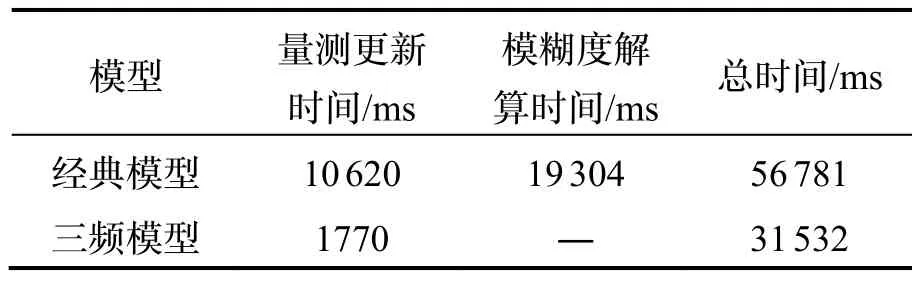
表1 可视卫星数9颗时的时间消耗Tab.1 Time consumption of situation with 9 available satellites

② 三频模型的总时间是经典模型的 55.53%。总时间的差异不如量测更新时间的差异那么悬殊，这是因为状态更新部分的时间占比大。

由图3看出：随着卫星数增加，经典模型的时间消耗会急剧上升；但三频模型的量测更新时间和总时间增加都比较平缓，特别是总时间变化不大，说明卫星数的增加对三频模型运算负担的影响不显著。分析三频模型的结构可知：相较于经典模型，三频模型既不需要构建伪距观测方程，也不需要计算浮点解及其协方差阵，这大大降低了量测更新时的矩阵维数，减少了时间消耗。

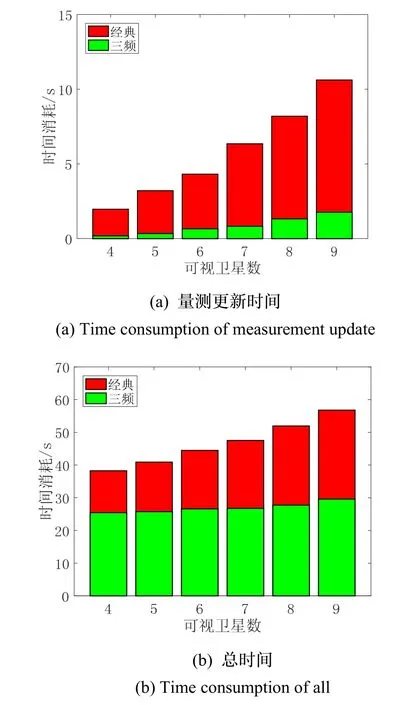
图3 不同可视卫星数对应的时间消耗Fig.3 Time consumption of situations with different available satellites

若将经典模型直接用于多频实时处理，会增加用于组合导航系统数据融合处理的芯片或板卡的设计复杂度、耗电量、实时解算负担。而三频模型可以避免上述问题，这对控制成本、提高可靠性甚至增强续航能力都是有益的。此外，对于事后处理，也能提高软件效率。

4.2 TCAR算法正确率和定位精度

三频模型的关键部分是TCAR算法解算模糊度整数解。短基线情况下，TCAR算法理论上有100%的正确率。但是受观测条件、接收机性能和卫星系统误差的影响，观测量的精度难以保证，这对基于无几何模型的直接取整影响较大，因而难以实现模糊度整数解的100%正确，使得TCAR算法不如LAMBDA算法稳定[18]。为分析TCAR算法和三频模型的相互影响，首先检验TCAR算法的效果。

LAMBDA算法更稳定可靠，因此将LAMBDA算法的整数解作为参考值，统计TCAR算法的正确率，如表2所示。历元总数为2008，高度截止角为15°，LAMBDA算法的ratio值设置为3。需要补充说明的是，C04、C05是低高度角GEO卫星，本次观测存在较大的误差，对不稳定的历元，没有纳入计算。

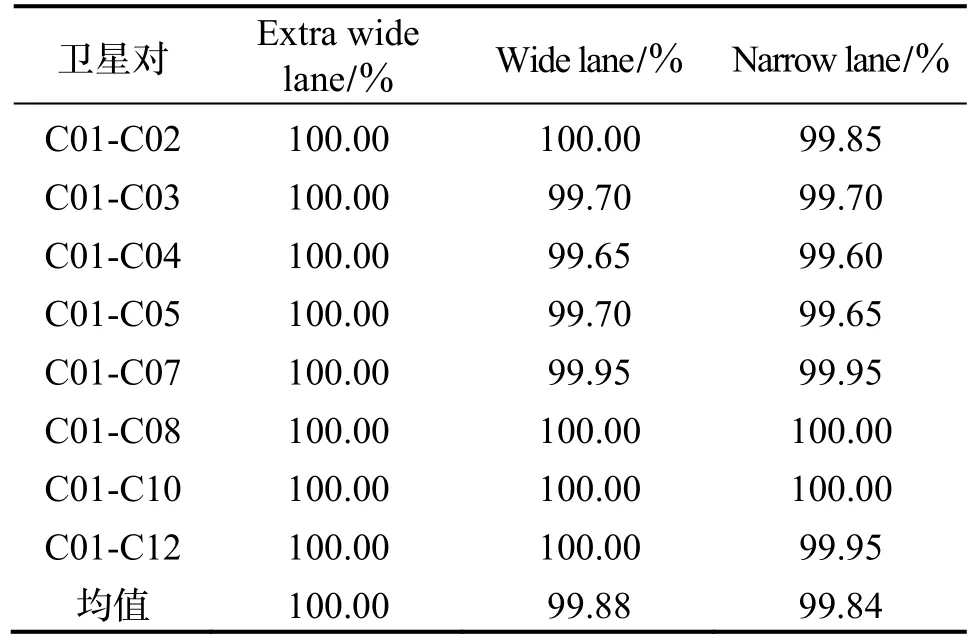
表2 TCAR模糊度解算正确率Tab.2 Ambiguity resolution success rate of TCAR

由于只有当所有卫星对的模糊度都解算正确时，该历元的定位结果才为正确的整数解，因此统计了所有卫星对模糊度都正确固定的历元数，得到TCAR算法的实际正确率为99.55%。

以LAMBDA算法的定位结果作为参考值，得到TCAR算法的定位误差如图4所示。其中，图4(a)是直接利用TCAR整数解进行定位计算得到的结果，图4(b)则多了整数解验证过程。对TCAR整数解错误的历元，使用浮点解。

由图4可知，当TCAR失败时，若直接使用错误的整数解，将使结果产生米级以上的误差。若用浮点解代替错误的整数解，仍会有分米级的误差。可见，TCAR算法由于模糊度解算的不稳定，还具有局限性。

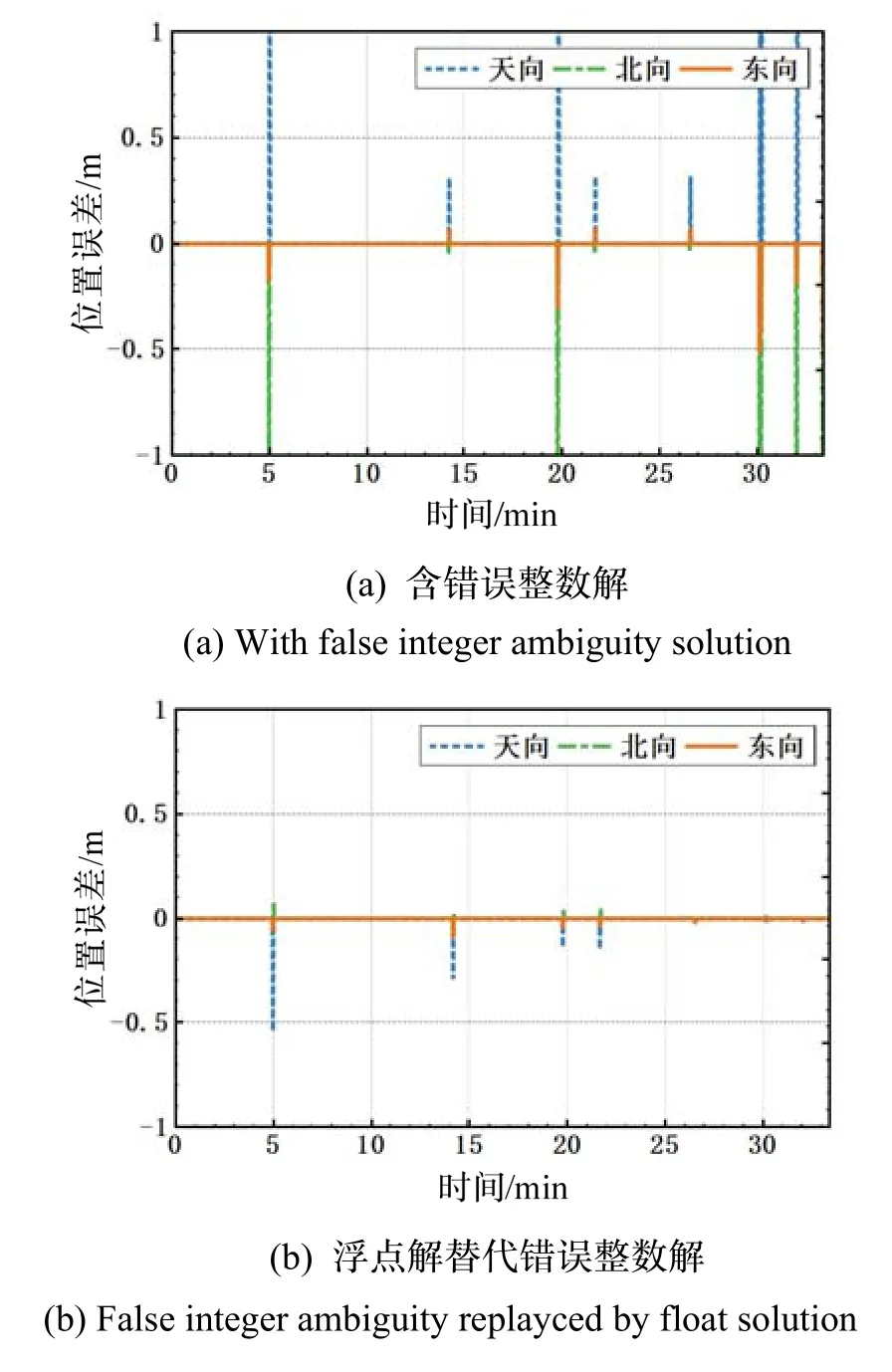
图4 使用TCAR模糊度解的位置误差Fig.4 Position errors with TCAR integer ambiguity solution

4.3 三频模型的验证

将经典模型得到的位置、速度、姿态解作为参考值，验证三频模型，其误差如表3和图5所示。可知三频模型与经典模型的位置、速度、姿态解相差不大，位置RMS在毫米级。比较图4(b)和图5位置误差可知，TCAR算法失败时，浮点解的误差可达0.5 m，但在基于TCAR算法的三频紧组合，这一误差已被紧组合中的惯导位置所校正。也就是说，三频紧组合能够很好地削弱 TCAR算法不稳定对定位结果的影响。速度RMS在厘米级，这是因为计算RMS时包含了初始历元的误差较大的数据，滤波稳定后速度误差是优于厘米级的。姿态误差存在规律性波动，这是因为，载体绕圈行驶，姿态频繁规律性变化造成经典模型和三频模型滤波效果不同，对姿态的估计也出现差别。实际上这一差别很小，低于0.01°。航向角偏差稍大，这是因为车载体作平面运动，对航向角的可观测度低。需要指出的是，经典模型得到的位置、速度、姿态解并不一定是真值。作此比较的目的是验证三频模型在理论上并无谬误，并且两者的位置、速度、姿态解结果相当，可验证其正确性。

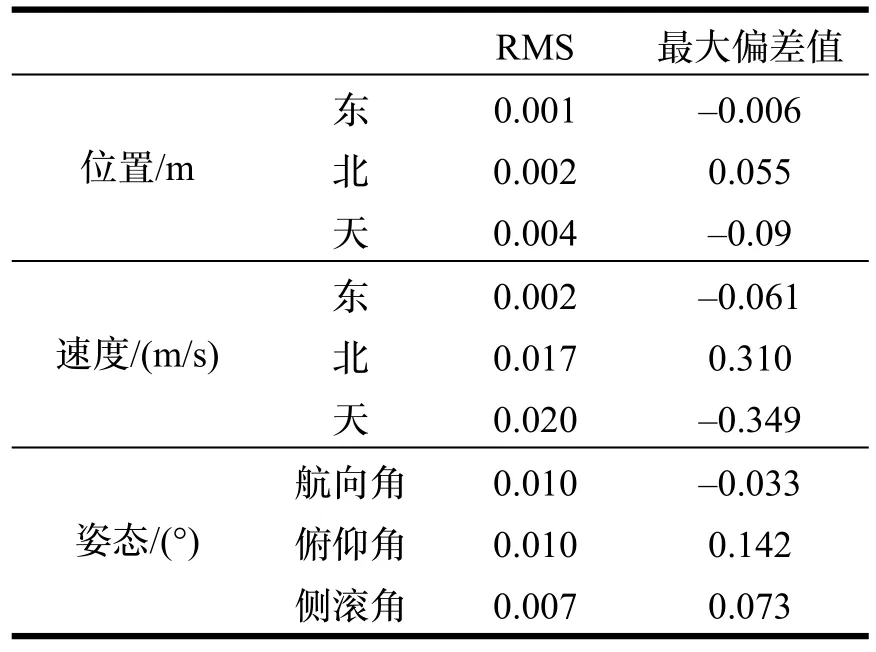
表3 三频差分GNSS/INS紧组合模型的误差Tab.3 Errors of triple-frequency differential GNSS/INS tightly coupled integrated model

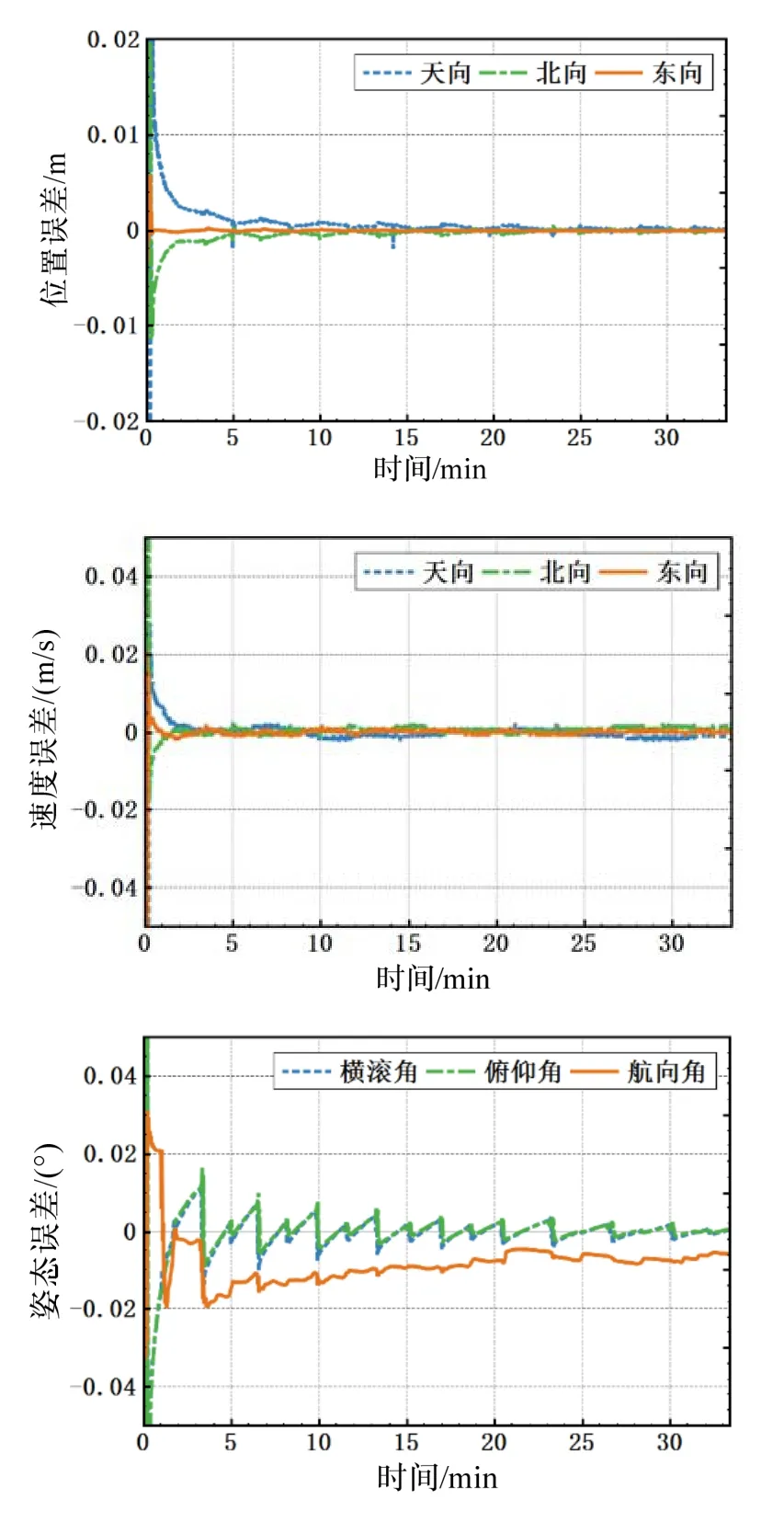
图5 三频差分GNSS/INS紧组合模型的误差Fig.5 Errors of triple-frequency differential GNSS/INS tightly coupled integration model

图6给出了加速度计和陀螺的零偏估计值，可以看到经过一段滤波后，估计值趋于常值，且与标称的参数相当，也辅助验证了三频模型的正确性。

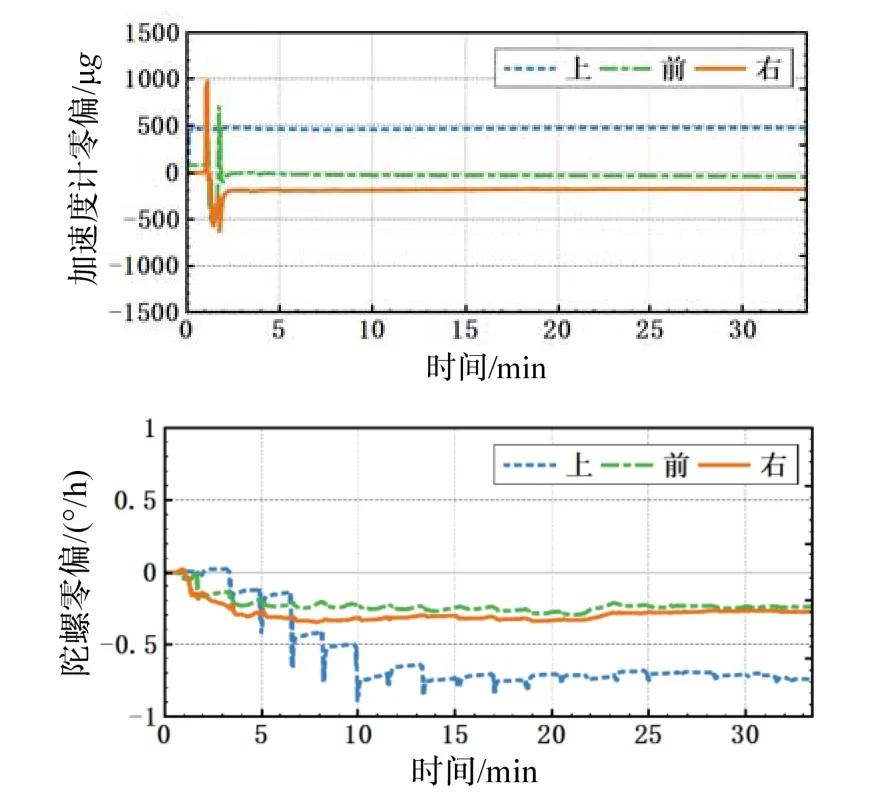
图6 零偏估计值Fig.6 Zero bias estimations

5 结 论

针对三频信号，研究了适用的GNSS/INS紧组合模型，评估了三频差分GNSS/INS紧组合模型的时间消耗和精度，得到了有益的结论：

① 三频差分 GNSS/INS紧组合模型有效地避免了三频信号带来的滤波阶数增加和运算负担问题。相较于经典模型，三频模型的解算效率具有显著优势。

② 制约三频差分 GNSS/INS紧组合稳定性和精度的主要因素是模糊度参数能否被正确解算。在本文算例中，单卫星导航解算时，TCAR算法正确率为99.55%，即便使用浮点解代替错误的整数解，且某些历元的位置精度仍受到严重影响，达到0.5 m的误差，但经过组合后，这一误差被削弱，组合导航解具有很优的精度。

该模型可用于三频信号的组合导航解算，特别是实时动态精密定位，获得时间优势和与经典模型相当的精度。下一步工作在于研究INS辅助对三频模糊度解算的优化，以提高模糊度解算正确率，增强三频差分GNSS/INS紧组合模型的可靠性。

参考文献（References）：

[1] Liang X, Huang Z G, Qin H L, et al. GNSS multifrequency multi-system highly robust differential positionning based on an autonomous fault detection and exclusion method[J]. IEEE Access, 2017, 5: 26842-26851.

[2] Zhang X H, He X Y. BDS triple-frequency carrier-phase linear combination models and their characteristics[J].Science China Earth Science, 2015, 58(6): 896-905.

[3] Forssell B, Harris R A, Martin-Neira M. Carrier phase ambiguity resolution in GNSS-2[C]//Proceedings of ION GPS. Institute of navigation, Kansas City, USA, 1997:1727-1736.

[4] Jung J. High integrity carrier phase navigation for future LAAS using multiple civilian GPS signals [C]//Proceedings of ION GPS. Institute of navigation, Alexandria,USA,1999, 99: 14-17.

[5] Zhao Q L, Dai Z Q, Hu Z G, et al. Three-carrier ambiguity resolution using the modified TCAR method[J]. GPS Solutions, 2015, 19(4): 589-599.

[6] Wu M K, He J, Wang H C. Reliable single epoch ambiguity resolution for precise attitude determination using BeiDou triple-frequency observations[J]. Journal of Chinese Inertial Technology, 2016, 24(5): 624-632.

[7] Tian Y J, Zhao D Q, Chai H Z, et al. BDS ambiguity resolution with the modified TCAR method for mediumlong baseline[J]. Advances in Space Research, 2017, 59(2):670-681.

[8] Paul D. GNSS与惯性及多传感器组合导航系统原理(第二版)[M]. 北京:国防工业出版社, 2015: 513-519.

Paul D. Principles of GNSS, inertial, and multisen- sor integrated navigation systems [M]. 2nd Edition. Beijing:National Defense Industry Press, 2015: 13-519.

[9] Falco G, Gutiérrez M C C, Serna E P, et al. Low-cost real-time tightly-coupled GNSS/INS navigation system based on carrier-phase double-differences for UAV applications[C]//Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2014). Tampa, FL, USA, 2014,812: 841-857.

[10] 韩厚增, 王庆, 王坚. 单频GPS/BDS/MEMS IMU紧组合模糊度固定抗差模型[J]. 中国惯性技术学报, 2015,23(4): 493-499.

Han H Z, Wang Q, Wang J. Robust ambiguity resolution for single-frequencyGPS/BDS/MEMS IMU tightly coupled system[J]. Journal of Chinese Inertial Technology,2015, 23(4): 493-499.

[11] Wang J, Han H Z, Meng X L, et al. Robust wavelet-based inertial sensor error mitigation for tightly coupled GPS/BDS/INS integration during signal outages[J]. Survey Review, 2016, 49: 419-427.

[12] Teunissen P J G, Oliver M. Springer handbook of global navigation satellite systems[M]. Springer International Publishing, 2017: 673-676.

[13] 郝万亮. SINS/DGPS组合定位定姿数据处理技术研究[D]. 郑州: 解放军信息工程大学, 2015.Hao W L. Research on data processing technology of position and orientation based on SINS/DGPS integration[D]. Zhengzhou: Information Engineering University, 2015.

[14] 刘帅, 孙付平, 张伦东. 模糊度固定解 PPP/INS紧组合模型[J]. 系统工程与电子技术, 2016, 38(10): 2389-2394.

Liu S, Sun F P, Zhang L D. Research on the tight integration of ambiguity-fixed PPP and INS[J]. Systems Engineering and Electronics, 2016, 38(10): 2389-2394.

[15] Li B. Review of triple-frequency GNSS: ambiguity resolution, benefits and challenges[J]. The Journal of Global Positioning Systems, 2018, 16(1): (1-11).

[16] 谢建涛. GNSS多系统多频精密相对定位理论与算法研究[D]. 郑州: 信息工程大学, 2016.

Xie J T. Research on theory and algorithms based on multi-GNSS & multi-frequency precision relative positionning[D]. Zhengzhou: Information Engineering University,2016.

[17] Ning Y, Yuan Y. A modified geometry-and ionosphericfree combination for static three-carrier ambiguity resolution[J]. GPS Solutions, 2017, 21(4): 1633-1645.

[18] Zhang X H, He X Y. Performance analysis of triplefrequency ambiguity resolution with BeiDou observations [J]. GPS Solutions, 2016, 20(2): 269-281.