基于LES的泵站前池表面涡及液下涡流瞬态特性分析

潘 强 施卫东，2 赵瑞杰 张德胜

(1.江苏大学流体机械工程技术研究中心， 镇江 212013; 2.南通大学机械工程学院， 南通 226019)

0 引言

泵站前池或泵站进水池是供水泵或吸水管直接吸水的水工建筑物，搭配大流量轴流泵常用于防洪抗旱、工农业用水以及大型电厂或核电站的冷却系统。实验表明，在泵站进水池内部不同工况的流动中存在多种旋涡，根据诱发位置可分为自由表面涡和液下涡，这些高度不稳定的旋涡会影响水泵吸入口的流态，不仅会造成叶轮载荷的不均匀分布，影响运行效率，甚至引起水泵汽蚀，产生噪声及震动，严重时导致水泵不能正常运行[1-2]。而流态良好的进水池可以保证机组的运行效率和泵站的稳定性。

为研究吸水池的内部流场，对吸水池进行性能评估或优化设计，常按照原型缩放后进行模型实验。LI等[3]采用二维PIV(Particle image velocimetry)测量了开式进水池的流态，结果表明，进水管周围流场受来流流速及进水管淹没深度的影响很大；MANSA等[4]用PIV测量了装有“T”型消旋器的闭式进水池流场，得到了良好的流态；SUERICH-GULICK等[5-6]通过实验研究了自由表面涡在水电站进水池内的形成机理，提出了一个半经验模型去预测涡特性。这些结果与理论的Burger涡模型十分相似，但模型实验经过缩放后虽然保证了Fr数相似，却无法满足Re数相似，在预测湍流及湍流粘度上存在误差。同时，涡结构与周围流场的相互作用很难通过实验来获得，而CFD(Computational fluid dynamics)提供了更高分辨率的流场信息。CONSTANTINESCU等[7-9]、RAJENDRAN等[10]先后采用标准k-ε、RNGk-ε和SST模型对泵站进水池的内部流动进行了数值模拟，提出了数值计算的可行性，但在瞬态流场及湍流的捕捉上存在误差；OKAMURA等[11]对比了不同数值计算软件、网格数、湍流模型的计算结果并与实验值对比；CHUANG等[12]用流体体积函数(Volume of fluid，VOF)处理自由表面，模拟进水池的流动，并与ADV(Acoustic doppler velocimetry)的实验结果对比；LUCINO等[13]采用FLOW- 3D模拟出表面涡、壁面涡和附底涡，并在表面涡观测到了液面凹陷；AKIHIKO等[14]采用λ2准则的等值面将水电站进水池中的涡结构可视化；王福军[15]对比了不同湍流模型在旋转流数值计算中的适用性问题；宋希杰等[16]分析了水流压力脉动的时域特性、频域特性及进水池底部喇叭管下方的压力分布，揭示了水流压力脉动规律及压力分布与漩涡之间的关系。以上研究结果表明，雷诺时均模型可以得到较为准确的时均流场信息，如速度、涡量与实验值的吻合度较高，但在瞬态参数的预测上与实验值有很大出入。相比于RANS(Reynolds-averaged Navier- Stokes equations)方法，大涡模拟(Large eddy simulation，LES)可以提供更为准确、精细的瞬态流场信息[8-9,14,17]，但在泵站进水池的数值研究中仍缺乏LES系统的验证及分析。

本文采用LES及VOF方法研究泵站进水池内附底涡的时空特性，对数值计算结果进行系统验证，包括近壁面网格及体网格尺寸、涡流区SGS(Sub-grid scale)模型求解湍动能比例以及与实验结果对比，并分析数值计算与实验结果差异产生的原因。基于LES的非定常计算结果，采用λ2准则观测自由表面涡及附底涡形态，讨论旋涡的时均特性和瞬态特性。

1 数值方法

1.1 几何模型

本文采用的泵站进水池物理模型是RAJENDRAN等[10]进行PIV实验的模型，如图1所示。进水池长1.22 m，宽0.3 m，高0.46 m，图中吸水管内径d为0.075 m，喇叭口直径D为0.115 m，对称布置在与后壁距离为1.4d的位置，泵管内流量0.004 m3/s，管内流速Up为0.9 m/s，水位高度4.5d，进水池横截面平均流速Um为0.03 m/s。管内Re数75 000左右，进水池内Re数10 000左右，Fr数和Wb数分别为1.1和840。

图1 进水池三维示意图Fig.1 3-D schematic of pump sump

1.2 控制方程

在整个计算域生成六面体结构化网格，不可压缩流体介质的质量和动量守恒方程在ANSYS CFX中求解，LES中的滤波尺度与局部网格尺度一致，比滤波尺度小的涡对流场的影响通过亚格子模型求解，滤波后的控制方程为

(1)

(2)

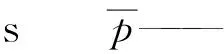
ρ——密度，kg/m3

ν——运动粘度，m2/s

gi——重力加速度，m/s2

τij——亚格子尺度应力，m2/s2

根据Boussinesq假定τij表达式为

(3)

(4)

(5)

(6)

式中τkk——同向的亚格子应力，m2/s2

δij——克罗内克函数

vsgs——亚格子湍流粘度，m2/s

Δ——网格尺度，m

Cw——WALE常数，取0.5

采用WALE模型求解亚格子应力，该模型克服了Smagorinsky模型耗散过大的问题，可以合理地重现层流及湍流过渡。

1.3 自由表面处理

VOF模型是一种在欧拉网格下的表面追踪方法，可以有效地模拟出具有明显界面的两相流动[12]。通过在水- 空气交界面求解含有某一相体积分数的控制方程来追踪运动界面，公式为

(7)

式中x、y、z——坐标轴方向

u、v、w——速度分量，m/s

φ为各相体积分数，当φ为1时则网格中充满该相流体，当φ为0时则网格中充满另一相流体，当φ在0～1之间时则含有界面，如此通过φ函数实现对运动界面的追踪。

1.4 边界条件及设置

泵站进水池中的流态受进口边界条件影响很大[2,12]，采用速度进口并保持速度分布与实验值一致[10]。虽然模拟与实验难以保证进口处的湍流度一致，但进水池入口与泵管之间的距离足够湍流的充分发展。为了保证水位恒定，采用流量出口并保证进出口流量差为零。进水池内的初始压力分布通过CFX软件中的表达式语言CEL设置。此外，壁面设置为无滑移且光滑，空气域的顶面设置为opening，允许空气流出或流入边界。瞬态控制方程的离散采用有限体积法，对流项采用中心差分，瞬态项采用二阶隐式后插法。非定常计算以稳态结果为初始值，时间间隔为0.002s，可以捕捉更为精细的流场信息。

1.5 网格分辨率

对于LES方法而言，网格尺度对计算精度的影响很大，粗糙的网格会导致大部分湍动能通过亚格子模型求解而不是直接求解，精细的网格则需要大量的计算资源。本文所用计算域网格单元数为6.2×106，对近壁面区网格进行了加密，使y+值(近壁面第1层网格的无量纲厚度)在1～3之间，并以1.1的增长率逐渐增加。CELIK等[18]采用相同物理模型、不同网格数的两套模型来计算LES方法中所用网格尺度的分辨率指数，得到两套网格中直接求解的湍动能占比，细网格和粗网格中直接求解的湍动能占比公式为

(8)

(9)

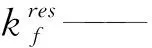
p——数值格式精度，取2

α——网格尺度比

采用一套数量为1.2×107的网格用以验证直接求解的湍动能占比，如表1所示，两套网格都直接求解了大部分湍动能。

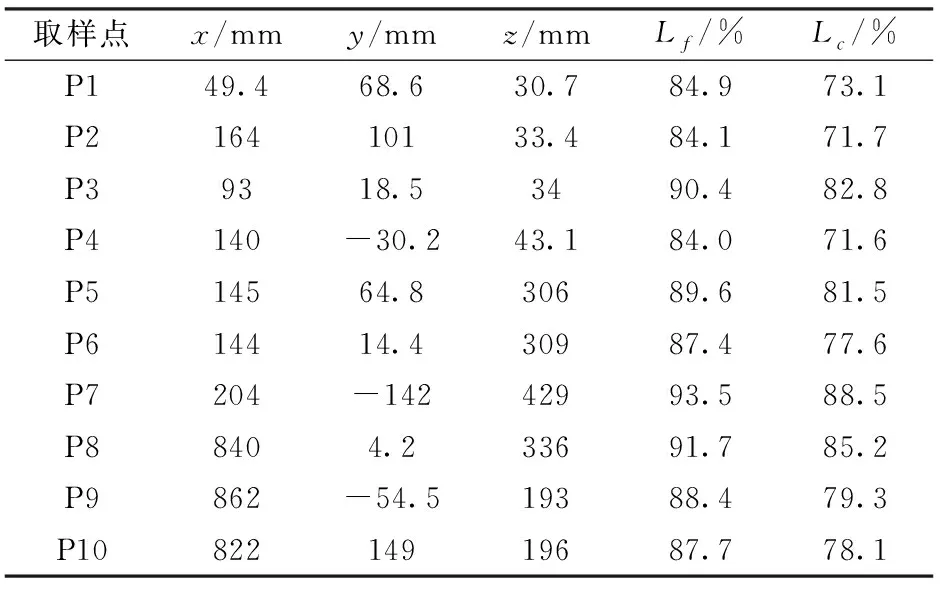
表1 涡流区10个取样点上求解的湍动能占比Tab.1 Proportion of resolved turbulence kinetic energyat 10 points in representative regions

2 实验对比验证

图2 模拟结果与实验对比Fig.2 Comparisons of LES and experiment results for three kinds of vortices

数值计算结果与RAJENDRAN等[10]的实验数据进行了对比，包括自由表面涡及液下涡的位置、形状和强度。实验数据包括瞬态及时均流场信息，时均值通过在16 s内平均32幅PIV图像得到，而非定常数值计算的时间步长为0.002 s，足够进行实验对比及流场信息的捕捉。由于自由表面涡和侧壁涡对称分布在泵管两侧，具有相似性，因此只选择其中一个作为对比。图2(图中ωx、ωy、ωz表示涡量沿x、y、z方向的分量)为后壁涡、左侧壁涡和自由表面涡瞬态流线图及时均涡量图的对比，可以发现，所有涡的瞬态流线与实验值十分吻合，包括涡的位置及形状。在时均涡量图中，模拟出的涡核数与实验值一致，如后壁涡和左侧壁涡的模拟结果与实验结果中都可看到3个涡核。然而，在涡量时均图中，涡核位置与实验值也存在出入，分析原因如下：首先，实验和数值计算难以保证进口条件完全相同，尤其是进口湍流度无法统一，在RAJENDRAN的实验中也可以发现，流场极度不稳定；其次，16 s内的32幅PIV图像只能得到相对的时均信息，在数值计算中也是如此，时间间隔越大得到的时均信息才越准确。总体来看，本文采用LES及VOF方法模拟进水池中的流动，与实验值结果吻合良好，与RANS方法相比，在涡尺度、位置、形状、涡量及涡核内湍动能预测方面优势明显[9,17]。

3 结果与讨论

3.1 涡流时均特性

采用LES方法模拟出旋涡结构，将压力最低点定义为涡心，得到平均切向速度Vθ沿半径方向的分布，并将Vθ的极值处半径定义为涡核半径，即旋涡特征半径，公式为

(10)

式中R——以涡心为圆心的任意半径，m

Γ——在半径为R的圆内的速度环量，m2/s

图5 自由表面涡λ2等值面Fig.5 Iso-surface of λ2 for free-surface vortex

由于前水池内液流的高度不稳定性，为得到3种旋涡的时均切向速度及环量分布，在距离自由表面或壁面10 mm的平面上，对16 s内的32个瞬态结果取平均值，该时均方法与实验中所用方法一致[10]。如图3和图4所示，3种涡的切向速度分布均展现出与理论涡模型一致的分布特点。其中，自由表面涡特征半径及环量较大，而附底涡在涡核内的速度梯度较大，其切向速度沿半径方向快速增加至极值，表现出较小的旋涡半径。这是由于附底涡在喇叭口的正下方，较强的抽吸力导致旋涡轴向速度拉伸，形成更加凝聚的涡结构。侧壁涡距离喇叭口较远，抽吸力较弱，表现出十分平缓的速度分布。由于粘性耗散，切向速度在涡核外逐渐降低，速度环量趋向平稳。基于RANS方法的数值计算会假设湍流的各项同性，从而过度地预测涡在半径方向上的耗散，往往得到较大的涡核半径及较小的旋涡强度[8]，相比于RANS方法，LES方法得到的旋涡结构更加符合真实流动。

图3 平均切向速度分布曲线Fig.3 Distribution of tangential velocity for three vortices

图4 速度环量分布曲线Fig.4 Distribution of circulation for three vortices

3.2 自由表面涡瞬态特性

由于自由表面涡对称分布在泵管两侧，因此选择其中之一的左侧壁涡，讨论其在3个时刻、0.2 s间隔下的瞬态特性。常见的旋涡结构定义方法有Q准则、λ2方法和Δ方法等，本文采用λ2等值面来对旋涡结构进行可视化处理，公式为

(11)

式中λ2——速度梯度张量的二阶不变量

通过设定λ2的阈值，可将自由表面涡与周围湍流区分开。如图5d(图中T1、T2、T3表示时间间隔为0.2 s的3个时刻)所示为自由表面涡渐弱过程，λ2等值面的阈值为200 s-2，可以清晰看到泵管边的自由表面涡(结构B)，自由液面为结构A，可见液面凹陷位置与涡位置保持一致，自由表面涡主涡周边环绕的二次涡为结构C，来源于泵管壁面的流动分离。随着液流下沉，结构C呈螺旋状环绕在主涡周边并与主涡相互作用，在图5b和图5c中可以看到主涡发生了弯曲变形，原因可归结于液面的波动或二次涡自旋的影响。此外，由于前水池内部流动的高度不稳定性，在图5中可以看到存在很多杂乱无章的涡流。

在自由液面下10 mm处，将笛卡尔坐标下的涡量换算为圆柱坐标，观察二维视角下，主涡与周围二次涡的演变，圆柱坐标的圆心为不同时刻下自由表面的涡心。图6所示为z轴方向的涡分量ωz，图7为沿圆周方向的涡分量ωθ，黑色十字表示涡心位置，其长度表示涡核大小。图6中可以看到，ωz变化不大，而涡核半径逐渐增大，说明旋涡强度在逐渐减弱，旋涡切向速度变得更为平坦，与图5一致。图7展示了主涡附近环绕着的二次涡，在三维视角下呈螺旋状逐渐靠近主涡并与之相互作用，一方面，二次涡的自旋会引起主涡震荡，造成主涡弯曲[19]，另一方面，这种相互作用会增加主涡和二次涡的动量耗散，图5中可以看到，二次涡很难随主涡下沉向喇叭口运动。由于自由表面的波动往往使涡流难以汇聚，这种二次涡环绕现象在附底涡中更为明显。

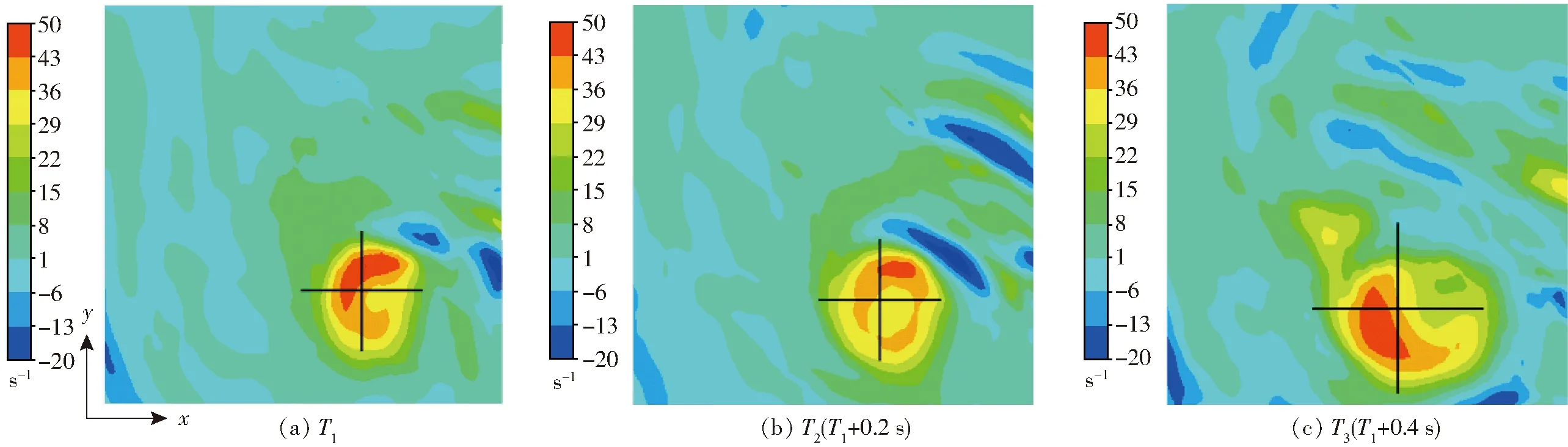
图6 3个时刻自由表面涡ωz云图Fig.6 ωz contours of free-surface vortex at three times

图7 3个时刻自由表面涡ωθ云图Fig.7 ωθ contours of free-surface vortex at three times

为进一步认识主涡及二次涡的演变，本文通过涡量方程中的对流项及弯曲、拉升项来分析涡量变化[20-21]，公式为

(12)

(13)

式中ω——涡量矢量，s-1

V——速度矢量，m/s

式(12)左边第2项为对流项，右边第1项为斜压作用项，第2项为拉伸、弯曲项，第3项为散度项，第4项为粘性耗散项。由于数值计算是基于不可压缩流动，式(12)左边第1项和第3项为零，并且在二维视角下讨论涡量的的输运过程，因此在xy平面上可将式(12)简化为式(13)。对流和弯曲、拉升可以造成涡量的重新分布，粘性力则会耗散涡量，包括分子粘性及亚格子粘性，但在高雷诺数流动中，粘性力耗散对涡量输运的影响很小[21]，因此在以下的分析中忽略不计。图8和图9分别为对流项及拉升、弯曲项对涡量变化的影响，从式(13)可以看出，对流项正值造成涡量减少，弯曲、拉升项正值使涡量增加。在图8中，速度对流在涡核内和涡核外对涡量的重新分布都有影响，这表明宏观流场对自由表面涡强度的变化起一定的作用，而图9中可以看到，拉升、弯曲项的作用主要存在于涡核内及边界处，两者的作用区域不同。对比图7和图9可以发现，在二次涡存在的区域，拉伸、弯曲对主涡的涡量改变明显，说明二次涡的自旋在一定程度上可以引起主涡轴向拉升或者弯曲，从而改变主涡沿z轴方向的涡量。从T1到T3时刻，涡核内部对流项及弯曲、拉伸项的极值区域减小并分散，这与主涡涡核半径逐渐增大，涡强度减弱相一致。

图8 3个时刻自由表面涡对流项云图Fig.8 Convection term of free-surface vortex at three times

图9 3个时刻自由表面涡拉伸、弯曲项云图Fig.9 Stretching/tilting term of free-surface vortex at three times

图10 附底涡λ2等值面Fig.10 Iso-surface of λ2 for floor-attached vortex

3.3 附底涡瞬态特性

由于前水池的几何对称性，往往会在底面产生交替出现且旋向相反的两个涡[10]，在本文中，只分析沿Z轴旋转的附底涡在3个时刻的瞬态特性。如图10(图中Ta、Tb、Tc表示时间间隔为0.2 s的3个时刻)所示，为了更好地呈现附底涡主涡与二次涡的结构，λ2的阈值随着时间逐渐减小，这也表明了主涡强度在逐渐减弱，与图10d一致。没有自由液面波动的影响，呈螺旋状环绕主涡的二次涡十分明显，随着时间的推进，二次涡向喇叭口方向运动，且旋转轴逐渐转变为与主涡一致的z轴方向。附底涡周围的二次涡与主涡的相互作用可以促进主涡的动量耗散，并引起主涡涡量的重新分布，从图10c可以看到主涡的弯曲。

图11展示了在距底面10 mm平面上的涡量分布图，从Ta到Tc涡量极值区域减小，涡强度减弱，在主涡涡核外侧，可以看到二次涡沿z轴的涡量ωz，由于二次涡向喇叭口方向运动，其方位角也在不断变化。图12为圆周方向的涡量分量ωθ，箭头所指的二次涡与图11中的位置相对应。可以看到在涡核外侧存在大量的环绕涡，并且旋向呈顺时针或逆时针，这个现象与自由表面涡相一致，但环量更加集中的附底涡会压缩ωθ呈现细长型的分布。图13和图14分别为对流项及拉伸、弯曲项对涡量输运的影响，可以看出在对流作用的影响下，涡核尤其是涡心附近的涡量ωz增加，而弯曲、拉升项引起涡量ωz的减弱，这说明在Ta到Tc过程中，二次涡的作用导致主涡弯曲、拉升是造成主涡ωz降低的主要原因。图14中的黑色虚线圆为二次涡位置，由于二次涡的旋向逐渐朝向z轴，其沿z轴方向的涡量不断增加，从Ta到Tc，二次涡逐渐远离主涡，主涡涡核内由于弯曲、拉升项引起的涡量降低逐渐减弱。

图11 3个时刻附底涡ωz云图Fig.11 ωz contours of floor-attached vortex at three times

图12 3个时刻附底涡ωθ云图Fig.12 ωθ contours of floor-attached vortex at three times

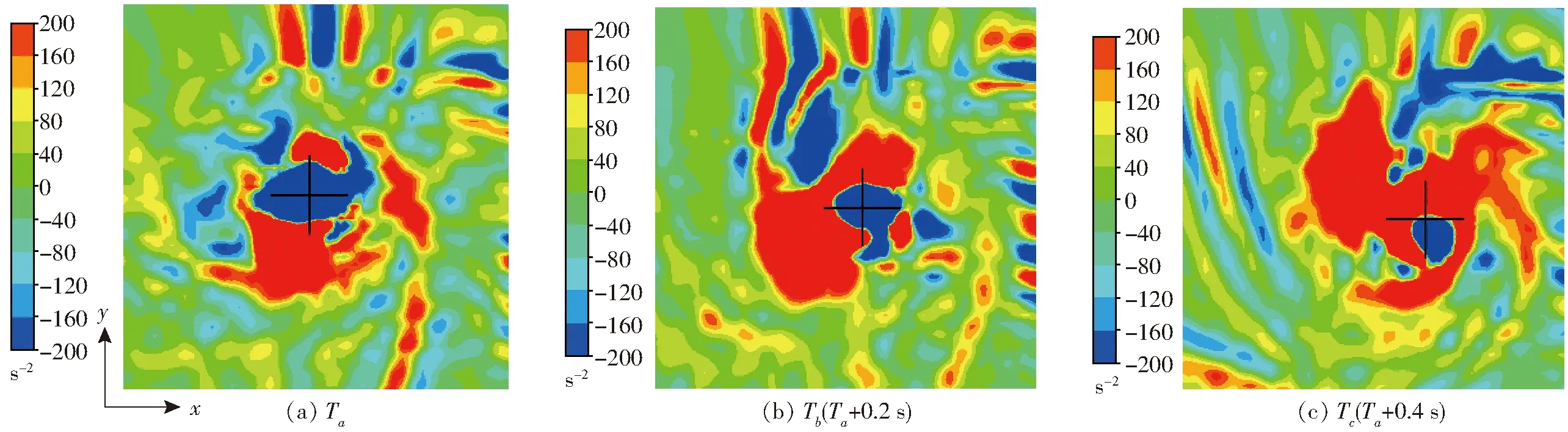
图13 3个时刻附底涡对流项云图Fig.13 Convection term of floor-attached vortex at three times

图14 3个时刻附底涡拉伸、弯曲项云图Fig.14 Stretching/tilting term of floor-attached vortex at three times

4 结论

(1)结合LES及VOF方法模拟泵站前水池内的旋涡流动，求解了两套不同数量的网格，结果表明细网格中直接求解的湍动能占比超过80%，粗网格中直接求解的湍动能占比超过60%。此外，将模拟结果与实验结果对比，3种典型涡的位置、大小、形状吻合度良好。

(2)相比于RANS方法会过度预测涡在半径方向上的耗散，LES方法预测得到的自由表面涡、附底涡及左侧壁涡的时均圆周速度、特征半径和环量分布更加符合真实流动特性。

(3)自由表面涡及附底涡的瞬态特性表明，在主涡涡核边界附近螺旋环绕着二次涡，且由于自由表面的波动使涡流难以汇聚，这种二次涡环绕现象在附底涡中更为明显。一方面，二次涡与主涡相互作用，增强主涡动量的向外耗散，另一方面，二次涡的自旋在一定程度上可以引起主涡轴向拉升或者弯曲，导致主涡涡量改变。

1 TSOU J L, MELVILLE B W, ETTEMA R, et al. Review of flow problems at water intake pump sumps[R]. New York: American Society of Mechanical Engineers, 1994.

2 ANSAR M, NAKATO T. Experimental study of 3D pump-intake flows with and without cross flow[J]. Journal of Hydraulic Engineering, 2001, 127(10): 825-834.

3 LI Y, WU Y, MANSA K, et al. The flow research in an open type pump sump by PIV experiments[C]∥ASME 2004 Heat Transfer/Fluids Engineering Summer Conference, 2004: 111-119.

4 MANSA K, ZHANG B, LI X, et al. PIV experimental investigation on the flow in a model of closed pump sump[J]. Tsinghua Science and Technology, 2003, 8(6): 681-686.

5 SUERICH-GULICK F, GASKIN S J, VILLENEUVE M, et al. Free surface intake vortices: theoretical model and measurements[J]. Journal of Hydraulic Research, 2014, 52(4): 502-512.

6 SUERICH-GULICK F, GASKIN S J, VILLENEUVE M, et al. Free surface intake vortices: scale effects due to surface tension and viscosity[J]. Journal of Hydraulic Research, 2014, 52(4): 513-522.

7 CONSTANTINESCU G S, PATEL V C. Numerical model for simulation of pump-intake flow and vortices[J]. Journal of Hydraulic Engineering, 1998, 124(2): 123-134.

8 RAJENDRAN V P, CONSTANTINESCU S G, PATEL V C. Experimental validation of numerical model of flow in pump-intake bays[J]. Journal of Hydraulic Engineering, 1999, 125(11): 1119-1125.

9 TOKYAY T E, CONSTANTINESCU S G. Validation of a large-eddy simulation model to simulate flow in pump intakes of realistic geometry[J]. Journal of Hydraulic Engineering, 2006, 132(12):1303-1315.

10 RAJENDRAN V P, PATEL V C. Measurement of vortices in model pump-intake bay by PIV[J]. Journal of Hydraulic Engineering, 2000, 126(5):322-334.

11 OKAMURA T, KAMEMOTO K, MATSUI J. CFD prediction and model experiment on suction vortices in pump sump[C]∥ The 9th Asian International Conference on Fluid Machinery, 2007:1-10.

12 CHUANG W L, HSIAO S C. Three-dimensional numerical simulation of intake model with cross flow[J]. Journal of Hydrodynamics, Ser. B, 2011, 23(3): 314-324.

13 LUCINO C, GONZALO DUR S. Vortex detection in pump sumps by means of CFD[C]∥XXIV Latin American Congress on Hydraulics, 2010: 21-25.

14 AKIHIKO N, NOBUYUKI H. Large eddy simulation of vortex flow in intake channel of hydropower facility[J]. Journal of Hydraulic Research, 2010, 48(4):415-427.

15 王福军. 流体机械旋转湍流计算模型研究进展[J/OL]. 农业机械学报, 2016, 47(2): 1-14.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160201&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2016.02.001.

WANG Fujun. Research progress of computational model for rotating turbulent flow in fluid machinery[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(2): 1-14. (in Chinese)

16 宋希杰,刘超,杨帆,等. 水泵进水池底部压力脉动特性实验[J/OL]. 农业机械学报,2017,48(11):196-203.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20171124&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2017.11.024.

SONG Xijie, LIU Chao, YANG Fan, et al. Experiment on characteristics of pressure fluctuationat bottom of pumping suction passage[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2017,48(11):196-203. (in Chinese)

17 TOKYAY T, CONSTANTINESCU S G. Large eddy simulation and Reynolds averaged Navier Stokes simulations of flow in a realistic pump intake: a validation study[C]∥World Water and Environmental Resources Congress, 2005.

18 CELIK I B, CEHRELI Z N, YAVUZ I. Index of resolution quality for large eddy simulations[J]. ASME Journal of Fluids Engineering, 2005, 127(5):949-958.

19 MARSHALL J S, BENINATI M L. External turbulence interaction with a columnar vortex[J]. Journal of Fluid Mechanics, 2005, 540: 221.

20 JI B, LUO X, ARNDT R E A, et al. Numerical simulation of three dimensional cavitation shedding dynamics with special emphasis on cavitation-vortex interaction[J]. Ocean Engineering, 2014, 87: 64-77.

21 JI B, LUO X, ARNDT R E A, et al. Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil[J]. International Journal of Multiphase Flow, 2015, 68: 121-134.