大型公共建筑建设中业主与项目管理公司的演化博弈

汪正云

（合肥财经职业学院工程学院，合肥230601）

博弈行为自古有之，1928年Von Neumann对博弈论基本原理的证明，成为博弈论的诞生标志。20世纪八九十年代博弈论与其他学科之间的关系走向成熟，之后伴随信息化技术和经济信息的发展，在经济领域得以广泛应用[1]。然而，传统博弈论认为参与者的行为完全理性，这点显然是不现实的，受到了越来越多的博弈论研究者的质疑[2]。对此，1973年Simon[3]引入生物学知识，提出了有限性经济主体的决策模型；1978年Taylor等[4]提出了基本的动态概念——模仿者动态或者复制动态；1995年Weibull[5]对演化博弈论进行了系统总结，从此，演化博弈论得到了广泛重视；进入21世纪，关于演化博弈论的研究又有进一步的发展，目前对演化博弈在经济领域中的应用成为热点[6]。

大型公共建筑的建设具有投资大、周期长、标准高、技术新、施工难、涉及面广等特点，在成本、技术、质量、进度、安全、信息等管理方面不可避免地会出现一系列问题[7-8]，因而对项目管理有着很高的要求。大型公共建筑建设的两个主要关联利益体——业主与项目管理公司在项目实施过程中，所采取的决策与管理“意欲合理,但只能有限达到”，是不可能完全理性的，亦即其最优策略不是一次性选择的成果，而是相互之间反复博弈并不断调整达到一种演化稳定状态的结果。项目管理公司在项目管理时往往模糊了自身发展与利益获得之间的关系，常因眼前一次性利益而失去企业信用，其结果则是失去市场机会，市场开发投入显著增加，最终影响到公司的长远发展。运用演化博弈方法可以通过合同的约束和项目实施过程中的表现促使双方管理向着有利于工程项目建设的方向发展。本文以某市体育场馆的建设为例，通过构建演化博弈系统，分析了业主与项目管理公司的博弈过程，以期为提升大型公共建设工程的项目管理提供一种方法和借鉴。

一、工程概况

某市开发区建设以体育文化设施和旅游设施为主，其中体育场馆占地面积58 200 m2，总建筑面积39 100 m2，工程投资总额为3.16亿元。为了顺利完成工程项目，不影响开发区的建设发展，开发区管委会（甲方，业主）与项目管理公司（乙方，项目管理方）签订项目管理协议合同，规定了双方的权责关系：甲方可对项目管理方面的事宜进行监督和建议，主要负责土地、规划、招标、竣工验收、资金支付等方面的工作；乙方负责全过程项目管理，即负责和协调前期策划、方案评审、经济分析、设计优化、专项评估、工程监理、工程款调度以及交通、消防、安全、环境评价等方面的工作。经双方协定，合同附加款里还增加了奖励与惩罚措施：1）项目保质按时完成，且节约了成本，则甲方按成本节支额的一定百分比给予乙方奖励提成；项目保质提前完成，且节约了成本，则甲方按照进度提前所带来的成本节支额的20%给予乙方奖励提成；2）乙方擅自变更建设内容、建设规模，未完全履行合同，所造成的投资增加以及工程质量的不合格等损失由乙方全部承担；甲方违反合同规定给乙方所造成的损失，据实赔偿损失额的50%；3）项目管理实施过程中如存在违纪违规事实，甲方有权终止合同，相应的项目损失由乙方负责。

二、演化博弈系统构建

（一）基本假设与动态复制方程建立

甲乙双方是有限理性的，其策略均有两种选择，即不违约A1，违 约A2，那么策略空间A={A1，A2}。假设T（ii＝1，2）为项目保质按时完成的收益，H（ii＝1,2）为项目保质提前完成的收益增加额，S（ii＝1，2）为自利违反合同规定造成对方利益受损的赔偿费用，Z（ii＝1，2）为自利违约获得的利益增加值，W为乙方违规违纪导致合同终止所造成的损失额。甲乙双方具体策略的支付矩阵见表1。

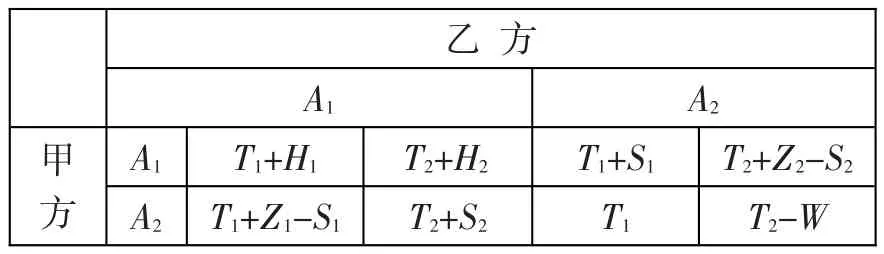
表1 甲乙双方支付矩阵

根据以上的博弈关系，构造甲乙双方之间的演化动态规律，也就是动态复制方程。假定甲方不违约的概率为p，违约的概率则为（1－p）；乙方不违约的概率为q，违约的概率则为（1－q）。那么:甲方选择A1的期望收益为

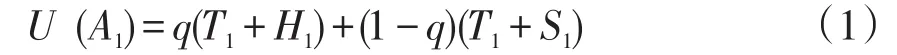
甲方选择A2的期望收益为

甲方的平均收益为

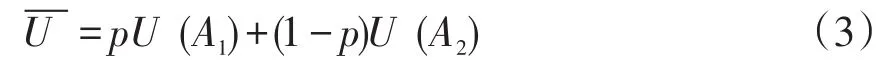
甲方不违约随时间的变化比率，即动态复制方程为

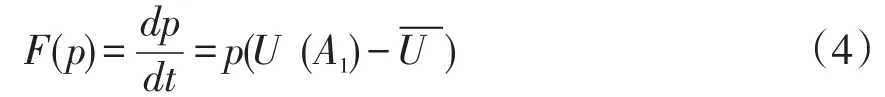
将式（1）（3）代入（4）得

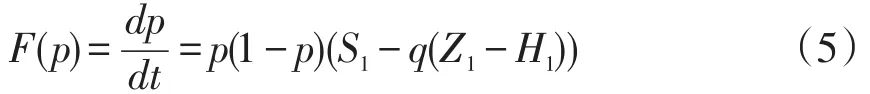
同理，乙方不违约的动态复制方程为

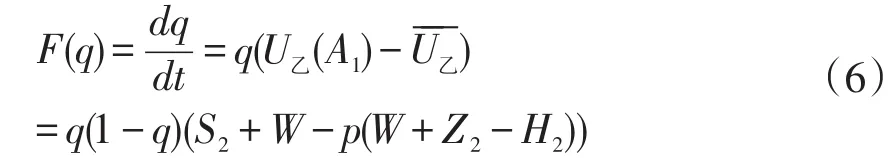
当F(p)=0、F(q)=0时，5个平衡节点是：E1(0,0),

当时，O点存在。

（二）稳定性分析

假设鞍点O存在，对式（5）、（6）分别求p和q的偏导数，得到Jacobian矩阵，即

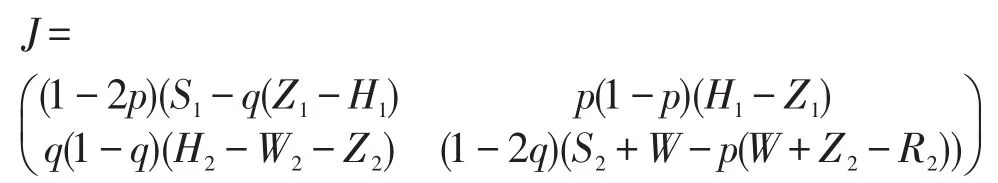
那么，接下来判定各平衡点处矩阵J的相应行列式（detJ）和迹的符号（trJ），分析结果见表2。

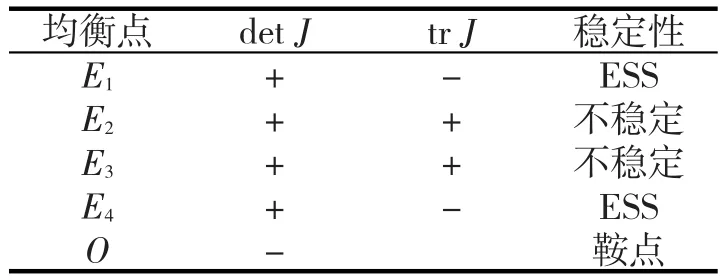
表2 平衡点的局部稳定性分析结果

从表2中可以看出，E1（0，0）和E4（1，1）点的稳定性是ESS，甲乙双方相对应的策略同时均不违约和同时均违约，即甲乙双方随着时间的推移，为了自身的利益，要么同时都选择不违约，要么同时都选择违约。E2（1，0）和E2（0，1）这两个点为不平衡点，O点为鞍点。甲乙双方博弈的复制动态演化过程如图1所示。

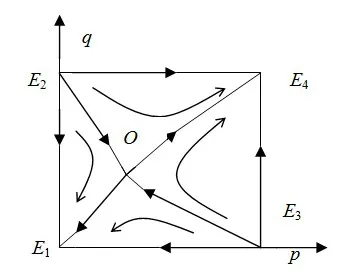
图1 甲乙双方演化博弈相位图

从图1中可以看出，演化博弈系统的收敛临界线为不平衡点E2（0，1）、E3（1，0）以及鞍点O连成的折线。初始状态在其下方区域E2OE3E1时，系统将收敛于点E1（0，0），即甲乙双方在演化过程中为了自身利益最大化均走向违约策略的趋势；初始状态在折线的上方区域E2OE3E4时，系统将收敛于点E4（1，1），即甲乙双方在演化过程中为了自身利益最大化均选择不违约策略的趋势。显然，E2OE3E4面积越大，甲乙双方均选择不违约的趋势越快，而这取决于鞍点O的位置。

（三）基本参数分析

1）项目保质提前完成的收益增加额Hi（i＝1,2）

合同中附加条款规定项目保质提前完成，且节约了成本，则甲方按照进度提前所带来的成本节支额的20%给予乙方奖励提成。倘若甲乙双方均不违约而实现项目目标，双方的收益是客观的，那么该条款必然促进双方积极履约，即结果是在其他变量不变的状况下，鞍点O向点E1（0，0）移动，E2OE3E4面积变大，Hi值增加。

2）为自利违反合同规定造成对方利益受损的赔偿费用Si（i＝1，2）

合同附加条款中规定乙方擅自变更建设内容、建设规模，未完全履行合同，所造成的投资增加以及工程质量的不合格等损失由乙方全部承担；甲方违反合同规定给乙方所造成的损失，据实赔偿损失额的50%。如果乙方违约造成了损失，那么甲方将从乙方保证金中扣除相应损失额，损失越多，赔偿额越高；同样，甲方违约，赔偿额按比例越高。这样，在其他变量不变的状况下，Si值越大，鞍点O向点E1（0，0）移动，E2OE3E4面积变大。显然，为了避免巨大损失，甲乙双方的博弈演化向着不违约而实现项目目标的方向发展越快。

3）乙方违规违纪导致合同终止所造成的损失额W

合同中附加条款规定项目管理实施过程中如存在违纪违规事实，甲方有权终止合同，相应的项目损失由乙方负责。在其他变量不变的状况下，W值越大，鞍点O就越向点E1（0，0）移动，E2OE3E4面积变大。乙方为了避免重大损失，在项目设计、材料采购、工程建设等项目管理过程中，会采取积极履约态度，博弈演化系统向着不违约方向发展。

从以上对Hi、Si、W的分析可知：合同中增加的附加条款对甲乙双方积极履行合约（不违约）具有重大作用；项目管理实施过程呈良性发展，双方博弈演化的最终方向是双方均采取不违约策略而实现项目目标。

（四）项目跟踪

项目2015年3月1日奠基，按照进度计划完成项目目标，工程建设中没有出现重大质量问题，于2016年9月30日交付使用。但是乙方仍然存在高素质人员和设备方面有配备不足的问题，并因此延误了工期，对此，甲方专门下函催促，并按照合同条约做出相应罚款。乙方汲取经验教训，在人员和设备方面采取对应措施，提高项目管理水平。整个项目建设历时22个月，甲乙双方朝着积极履行合约的方向发展，双方均获得满意的收益。那么，再自然不过的结果就是甲方在开发区的建设中继续委托乙方进行项目管理，乙方获得长期受益。

三、结语

之所以选择业主与项目管理公司作为大型公共工程项目管理研究的对象，是因为两者存在既监管又合作的关系，它们在项目实施过程中是主要的管理者和受益体，其管理策略直接影响项目的顺利实行。此外，囚徒困境是博弈论中非零和博弈著名的例示，为了研究的典型性及提高研究的参考价值，故而选择了业主与项目管理公司作为研究对象。

从以上的分析和工程的实际结果可以知道，通过构建演化博弈系统可以指导项目参与方的系统管理，使它们将整个工程建设视为一个动态过程，在这个过程中排除非最优的决策，引导项目参与方朝着积极的方向发展。大型公共建筑的建设不仅需要一流的设计和一流的技术，更离不开一流的管理，演化博弈论的应用无疑可以保证实现建设项目的整体目标，促进项目管理公司的长远发展。

[1]谢识予.经济博弈论[M].3版.上海:复旦大学出版社，2002：377.

[2]谢识予.有限理性条件下的进化博弈理论[J].上海财经大学学报，2001，3（5）:3-9.

[3]SIMON H A.Model of man:social and rational[M].New York:John Wiley and Sons,1973.

[4]TAYLOR P D,JONKER L B.Evolutionary stable strategies and game dynamics[J].MathematicalBiosciences,1978(40):145-156.

[5]WEIBULL J W.Evolutionary game theory[M].Cambridge:MIT Press,1995.

[6]王文宾.演化博弈论研究的现状与展望[J].统计与决策，2009（3）:158-161.

[7]丁北斗，崔杰，陈洁，等.结构健康监测系统及其在工程上的应用[J].徐州工程学院学报（自然科学版），2017，32（2）:72-76.

[8]赵小惠，王恒.高层建筑火灾初期人员疏散策略研究[J].徐州工程学院学报（自然科学版），2016，31（4）:27-32.