循环移位正交系数的测量矩阵改进算法

安冬冬,龚晓峰,陈思南

(四川大学 电气信息学院,成都 610065)

0 概述

传统奈奎斯特采样定律表明,想要准确地还原原始信号,采样率必须大于或等于信号最高频率的2倍。随着数字信号处理技术的不断发展,系统需要处理的数据量急剧增加,传统的奈奎斯特采样定理的弊端逐渐显现:采样得到的巨大数据,使得数据的传输与存储对于存储空间和硬件的数据处理能力的要求越来越严格,使信号采样技术的发展受到限制。因此,有必要研究既能降低数据量,又能较好地重构信号的技术。

文献[1-2]在信号稀疏表示和信号复原等理论基础上,针对稀疏可压缩信号,提出压缩感知(Compression Sensing,CS)理论,打破了传统Nyquist采样理论对采样频率的限制,将压缩和采样合并进行,大大减小了采样的数据量,使得数据的传输处理压力大幅减小。

在CS核心问题[3],即稀疏变换、测量矩阵构造和重构算法过程中,测量矩阵的相关性直接影响着重构的效果。测量矩阵分为随机矩阵和确定性测量矩阵2大类,随机矩阵中常用的是高斯随机矩阵和伯努利随机矩阵。虽然生成的测量矩阵与大多数稀疏信号不相关,重构性能较好,但需要很大的存储空间,以及由于数据随机生成,使得硬件难实现等缺陷,新的方法层出不穷。有的致力于研究如何减小存储空间,文献[4]提出STP-CS方法打破了矩阵相乘时对维数的限制,减小了测量矩阵的大小。文献[5]采用低密度奇偶校验码构造确定性测量矩阵。文献[6]提出存储迭代参数取代存储整个矩阵的方法来减小对存储空间的要求。有的致力于研究如何提高重构精度,文献[7]基于图像分块思想,运用 Toeplitz的块循环矩阵来构造测量矩阵,在重构效果和重构时间上,都有所提升。文献[8]采用混沌序列构造测量矩阵。文献[9]利用Legendre序列经过二次采样后得到确定性测量矩阵。文献[10]采用范德蒙矩阵构造的测量矩阵都在一定程度上提高了信号的重构精度。

本文提出一种新的确定性矩阵的方法。基于正交基线性表示改进法,使用随机数组成的行向量的循环移位法生成相关性低的正交系数,将哈达玛矩阵作为正交基。进而构造一种新的确定性测量矩阵,使用枚举查找的方法打破哈达玛矩阵的应用局限。

1 压缩感知基本框架

由观测值y通过重构算法重构原信号x,即求解以下问题:

(1)

但是,求解式(1)是欠定问题,文献[12]提出可以将式(1)的优化目标用l1 范数来代替:

s.t.y=Φx=Φψα

(2)

将式(1)的欠定求解问题转换成凸优化问题,再将其转换成线性规划求解的问题,完成对式(1)的求解。

文献[13]提出:当测量矩阵满足有限等距性质(Restricted Isometry Property,RIP)时,式(1)有唯一解,稀疏信号可以得到精确重建。

定义1传感矩阵R=Φψ的等距约束系数δ∈(0,1),θ为任意k稀疏向量,若R满足:

(3)

其中,ψ为稀疏基,Φ为测量矩阵,则Φ满足RIP。

RIP条件很难满足,所以,很多学者又将条件逐渐弱化。文献[14]提出:当测量矩阵Φ和系数基ψ不相关时,依旧可以将原信号进行较好的复原。这个条件与RIP是等价的,所以可以在信号稀疏表示后,通过构造与稀疏基不相关的测量矩阵,来完成信号的采集。文献[15]通过阈值收缩的方法减小Φ和ψ的不相关性,并提出一种基于最优投影的方法提高随机测量矩阵的非相干性;文献[16]提出QR分解法,通过增大矩阵的奇异值来优化测量矩阵;文献[17]提出基于耦合观测法降低测量矩阵与稀疏字典之间的相干性。

2 循环轮换构造的正交系数改进算法

文献[18]指出,在压缩比小于 0.5的情况下,正交系数的构造没有简单易控制的生成算法。针对这一问题,基于循环轮换矩阵与正交基线性表示的思想,本文提出一种新的测量矩阵构造方法。

使用正交基线性表示测量矩阵方法的关键在于找到合适的正交基和正交系数的组合。哈达玛矩阵由于其突出的正交性以及硬件易实现的特性,作为构造确定性测量矩阵的正交基有着独特的优势。但由于部分哈达玛矩阵[19]构造时,对于M的值有较高的特殊要求,这使得哈达玛矩阵的应用受到极大局限。本文通过改进,打破了构造哈达玛矩阵对于M的限制。对于正交系数的构造,使用随机行向量的循环轮转法,使得最终构造的测量矩阵有较低的相关性。

本文算法步骤如下:

步骤1将二维图像信号投影到小波变换域,得到二维图像的稀疏表示。

步骤2根据给定的N,依次找到0～N中满足哈达玛矩阵构造要求的所有数值,按从小到大排列组成一个行向量v。

步骤3根据给定的M,选择出v中第一个不小于M的符合要求的整数L,构成L×L的哈达玛矩阵H,得到构造测量矩阵所需的正交基。

这样对于任意的M,都能有对应的L×L的哈达玛矩阵与之对应,打破了哈达玛矩阵的使用局限。

步骤4使用步骤3的哈达玛矩阵H构成测量矩阵的前L列:

H=[h1,h2,…,hL]

(4)

其中,[hi],i=1,2,…,L为哈达玛矩阵列归一化后的向量。

步骤5关于正交系数的构造,本文针对压缩比小于0.5的情况提出一种新的方法,构造一个随机的1×N-L行向量:

b=[b1,b2,…,bN-L]

(5)

为满足系数的非零要求,将式(5)做了进一步的改进:找到其中最小的值bmin,然后将式(5)中所有值都加上|bmin|。为避免有互为相反数的情况出现,在得到的系数矩阵中各值再加上常数1,这样得到的系数向量满足不相关性和非零性。

步骤6按行循环轮换L-1次,得到L×N-L维的正交系数F:

(6)

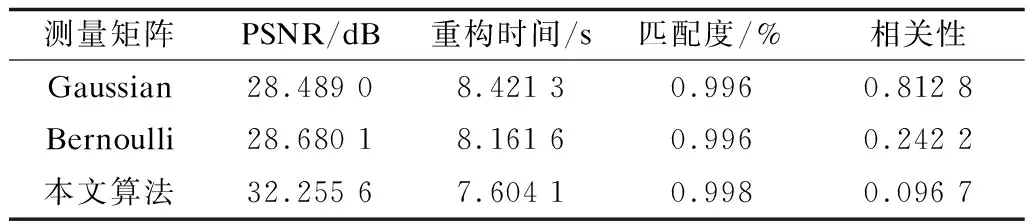
因为L

步骤7将规范正交基H与系数矩阵F相乘,得到测量矩阵剩下的N-L个列向量:

HH=H*F=[hh1,hh2,…,hhN-L]

(7)

步骤8将步骤4和步骤7得到的2个矩阵按列合并得到测量矩阵Φ:

Φ= [H,HH]=

[h1,h2,…,hL,hh1,hh2,…,hhN-L]L×N

(8)

步骤9在步骤8中得到的矩阵中任意选取M行,再进行列单位化即可得到最终M×N的测量矩阵。

步骤10使用变步长前后追踪算法恢复原始二维图像。

步骤11计算相关的评价图像恢复性能指标的参数。

3 实验设置与结果分析

本次实验使用分辨率为256×256像素的二维Lena图像,稀疏变换使用正交小波变换DWT将信号变换到小波域,测量矩阵分别采用Gaussian随机矩阵、Bernoulli随机矩阵和循环移位法生成正交系数的正交基线性构造改进方法,重构算法使用变步长前后追踪算法(Variable Step Forward Backward Pursuit,VSFBP)。使用峰值信噪比(Peak Signal to Noise Ratio,PSNR)、匹配度、运行时间和测量矩阵的相关性作为评价重构效果的参数。

1)二维图像峰值信噪比pPSNR的计算:

(9)

2)匹配度的计算:

(10)

3)重构时间为整个程序运行1 000次的平均时间。

4)测量矩阵的相关性:

(11)

其中,ai,aj为测量矩阵的行向量,〈ai,aj〉=ai·ajT为内积。

当M/N=0.5,为减弱实验的随机性带来的影响,使结果更准确,仿真时将每种测量矩阵生成方法都重复做了1 000次蒙特卡洛实验,求3种算法各自性能指标的平均值,结果如表1所示。

表1 M/N=0.5时测量矩阵的重构性能对比

由表1可以看出:在压缩比为0.5的条件下,本文提出的循环移位构造正交系数改进算法所构造的测量矩阵图像重构的PSNR比Gaussian随机矩阵和Bernoulli随机测量矩阵要高约3.5 dB,而且匹配度比两者高,程序运行的时间也更低,即本文算法的算法复杂度更低。同时本文算法构造的测量矩阵的相关性比高斯随机矩阵和伯努利测量矩阵的相关性都低,证明了本文算法的正确性,达到了最初降低测量矩阵相关性的目的。

为更直观地比较3种算法对二维图像的重构效果,只取M/N=0.5时3种测量矩阵构造算法所恢复的图像对比,如图1所示。

图1 各测量矩阵Lena图像重构效果对比

从图1可以看出,在压缩比相同的情况下,本文提出的新的确定性测量矩阵的重构效果比高斯随机测量矩阵和伯努利随机测量矩阵好,重构图像更清晰。为更全面地说明新的确定性测量矩阵有着更好的重构效果,将文献[20]提出的基于改进的哈达玛矩阵方法所构成的测量矩阵的效果重构结果复现,在M/N≤0.5的情况下,与本文的测量矩阵、Gaussian测量矩阵和Bernoulli测量矩阵的重构峰值信噪比进行对比,结果如图2所示。

图2 压缩比M/N≤0.5情况下的重构结果

由图2 可知,在M/N≤0.5时,文中提出的基于循环移位法生成正交系数的测量矩阵改进算法比文献[20]中的改进哈达玛矩阵法、Gaussian随机测量矩阵和Bernoulli测量矩阵的PSNR都要高。但当M/N=0.1时PSNR要比文献[20]中的改进哈达玛矩阵低,这是由于文中的测量矩阵生成时都具有随机性,虽然已经做了1 000次蒙特卡洛实验求平均值,但是这只能弱化随机性带来的影响,并不能消除该影响。

4 结束语

针对压缩比小于0.5时,没有确切有效的测量矩阵构造算法这一问题,基于正交线性表示法,本文提出遍历查找的算法,打破了哈达玛矩阵对被测量信号维数的限制,使得性能优良的哈达玛矩阵应用可以更广泛。并且相比传统的从高维正交矩阵映射获得测量矩阵的方法,对于压缩比较小的情况,本文算法减小了工作量;同时使用循环移位改进法构造正交系数,生成性能更好的测量矩阵。仿真结果表明,在压缩比小于0.5的情况下,本文算法的图像重构效果依旧很清晰,比高斯和伯努利矩阵的重构效果都好,由于采用向量的循环移位,对存储空间的要求大大降低,更利于硬件的实现,为压缩感知的应用提供了更广阔的空间。

[1] CANDES E J,ROMBERG J,TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.

[2] DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[3] 石光明,刘丹华.压缩感知理论及研究进展[J].电子学报,2009,37(5):1070-1081.

[4] PENG Haipeng,TIAN Ye,KURTHS J.Semitensor product compressive sensing for big data transmission in wireless sensor networks[EB/OL].[2017-03-22].https://doi.org/10.1155/2017/8158465.

[5] ZHANG Jun,HAN Guojun,FANG Yi.Deterministic construction of compressed sensing matrices from protograph LDPC codes[J].IEEE Signal Processing Letters,2015,22(11):1960-1964.

[6] RAVELOMANANTSOA A,RABAH H,ROUANE A.Compressed sensing:a simple deterministic measurement matrix and a fast recovery algorithm[J].IEEE Transactions on Instrumentation and Measurement,2015,64(12):3405-3413.

[7] 瞿广财,张淑芳,吕 卫.基于图像分块的Toeplitz结构测量矩阵设计[J].计算机工程,2012,38(16):212-214,218.

[8] ZENG Li,ZHANG Xiongwei,CHEN Liang,et al.Deterministic construction of toeplitzed structurally chaotic matrix for compressed sensing[J].Circuits Systems and Signal Processing,2015,34(3):797-813.

[9] 崔 翔,万洪杰.基于Legendre序列的确定性测量矩阵[J].计算机工程与应用,2016,52(16):116-120.

[10] 赵瑞珍,王若乾,张凤珍,等.分块的有序范德蒙矩阵作为压缩感知测量矩阵的研究[J].电子与信息学报,2015,37(6):1317-1322.

[11] 李文静,陈红卫.一种基于压缩感知的ISAR成像方法[J].计算机仿真,2015,32(8):10-14.

[12] DONOHO D,TSAIG Y.Extensions of compressed sensing[J].Signal Processing,2006,86(3):533-548.

[13] CANDES E J,TAO T.Decoding by linear program-ming[J].IEEE Transaction on Information Theory,2005,51(12):4203-4215.

[14] BARANIUK R.Compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-121.

[15] ELAD M.Optimized projections for compressed sensing[J].IEEE Transactions on Signal Processing,2007,55(12):5695-5702.

[16] 傅迎华.可压缩传感重构算法与近似QR分解[J].计算机应用,2008,28(9):2300-2302.

[17] 吴 赟.压缩感知测量矩阵的研究[D].西安:西安电子科技大学,2012.

[18] 李 浩.用于压缩感知的确定性测量矩阵研究[D].北京:北京交通大学,2011.

[19] CANDES E.The restricted isometry property and its implications for compressed sensing[J].Proceedings of National Academy of Sciences,2008,346(9-10):589-592.

[20] 马庆涛.压缩感知中的信号重构算法研究[D].南京:南京邮电大学,2013.