几类二重和三重线性码的构造

杜小妮,李晓丹,吕红霞,赵丽萍

(西北师范大学 数学与统计学院,甘肃 兰州 730070)

0 引言

文中假设p为奇素数,q=pm,m为正整数.由有限域Fq到Fp的迹函数[9]Trm(·) 定义为:

Trm(α)=α+αp+…+αpm-1, ∀α∈Fpm.

设F*q表示Fq中全体非零元素组成的集合,集合D={d1,d2,…,dn}⊆Fq,则Fq上长度为n的线性码定义为

称集合D为线性码CD的定义集.通过选择合适的定义集D可以构造一些较低重量的线性码[5].近年来,通过选择不同的定义集得到了几类较低重量的线性码[10-18].研究表明,恰当地选择定义集可以得到一些最佳码[8,19-20].

若m≥2为正整数,Li等[7]通过选取

构造了p元线性码

CD={c(a,b):a,b∈Fpm},

(1)

得到了几类二重和三重的线性码.其中

受文献[7]的启发,本文选择定义集

其中c∈F*p,l为正整数且l∈{1,2,pm/2+1},m≥2为正整数.下面讨论由该定义集构造的几类线性码的重量分布.

1 基础知识

首先给出指数和的一些结论以及证明主要结论需要用到的引理.

对任意的a∈Fq,Fq上的加法特征定义为

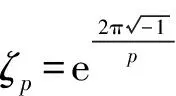
称Fq上乘法群F*q的特征为Fq的乘法特征[9],定义为

其中g是F*q的一个生成元.补充定义λj(0)=0.称乘法特征λ(q-1)/2为Fq的二次特征,用η来表示.

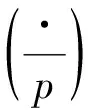
引理2[22-23]设λ为F*q上的一个N>2阶乘法特征.假设存在最小正整数f使得pf≡-1(modN).若m=2ft,t为某个正整数,则对1≤i≤N-1,有

引理3[9]设λ为Fq上阶为N=gcd(n,q-1)≥2的一个乘法特征,则对任意的a∈F*q,有

引理4[9]若f(x)=a2x2+a1x+a0∈Fq[x],其中a2≠0,则

引理5[24]设m=2s(s为正整数),a∈F*ps,b∈Fpm,则

引理6[6,13]对每个c∈F*p,有

引理7对每个c∈F*p,设

Mc={b∈F*q:Trm(bps+1)=c},

则|Mc|=pm-1+pm/2-1.

证明由引理2和引理3可得

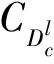
所以码长n=p2m-1-1.

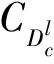
则码字的重量

W(c(a,b))=n-N(a,b),

(4)

且有

其中,

2.1 l=1的情形

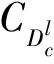
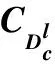
表1 码的重量分布

证明由(5)式可以得到

因而,依据(4)式可得到定理的结论. 】

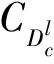
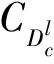
2.2 l=2的情形

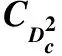
表2 m为偶数时的重量分布

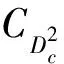
证明分以下4种情况来确定N(a,b)的值.

( i )若a=b=0,则由(5)式可得

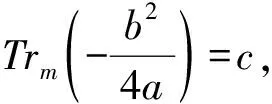
由引理6可知该值出现的次数为

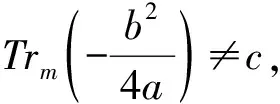
(iv)若a∈FqFp,b∈Fq或a=0,b∈F*q,则

显然该值出现的次数为(q-p)q+q-1,即

pm(pm-p+1)-1.

由(4)式可得到码的重量分布. 】

证明分以下3种情况来确定N(a,b)的值.

( i )若a=b=0,则

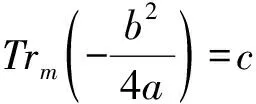
由引理6可知该值出现的次数为

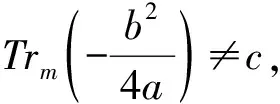
由(4)式可定义

其对应的重数分别为Aw1,Aw2,Aw3,根据MacWilliams方程[14]可得

解方程可得该码的重量分布. 】

2.3 l=pm/2+1的情形

令m=2s(s为一个整数).与l=2的情形类似可知,若a∉F*p则Ω3=0.若a∈F*p则由引理5有

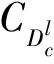
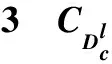
表的重量分布

证明依据引理7,该定理的证明方法与定理2的类似,此处不再赘述. 】

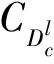
3 结束语

根据文献[6]的结论,文中构造的线性码可应用于秘密共享方案.

参考文献:

[1] YUAN Jin,DING Cun-sheng.Secret sharing schemes from three classes of linear codes[J].IEEETransactionsonInformationTheory,2005,52(1):206.

[2] DING Cun-sheng,WANG Xue-song.A coding theory construction of new systematic authentication codes[J].TheoreticalComputerScience,2005,330(1):81.

[3] CALDERBANK A R,GOETHALS J M.Three-weight codes and association schemes[J].PhilipsJournalofResearch,1984,39(4):143.

[4] KLØVE T.CodesforErrorDetection[M].Singapore:World Scientific,2007.

[5] DING Cun-sheng,LI Cheng-ju,LI Nian,et al.Three weight cyclic codes and their weight distributions[J].DiscreteMathematics,2016,339(2):415.

[6] DING Ke-lan,DING Cun-sheng.A class of two-weight and three-weight codes and their applications in secret sharing[J].IEEETransactionsonInformationTheory,2015,61(11):5835.

[7] LI Cheng-ju,YUE Qin,FU Fang-wei.A construction of several classes of two-weight and three-weight linear codes[J].ApplicableAlgebrainEngineeringCommunication&Computing,2017,28(1):11.

[8] XIANG Can,TANG Chun-ming,FENG Ke-qin.A class of linear codes with a few weights[J].Cryptography&Communications,2016,9(1):1.

[9] LIDL R,NIEDERREITER H.FiniteFields[M].Boston:Addison-Wesley Publishing Inc,1983:186.

[10] DING Cun-sheng.CodesfromDifferenceSets[M].Singapore:World Scientific,2014:356.

[11] DING Cun-sheng.Linear codes from some 2-designs[J].IEEETransactionsonInformationTheory,2015,61(6):3265.

[12] LI Fei,WANG Qiu-yan,LIN Dong-dai.Complete weight enumerators of a class of three-weight linear codes[J].JournalofAppliedMathematics&Computing,2017,55(1):733.

[13] LI Cheng-ju,YUE Qin,FU Fang-wei.Complete weight enumerators of some cyclic codes[J].Designs,CodesandCryptography,2016,80(2):295.

[14] LI Fei,WANG Qiu-yan,LIN Dong-dai.A class of three-weight and five-weight linear codes[J].DiscreteAppliedMathematics,https://doi.org/10.1016/j.dam.2016.11.005.

[15] LIU Li,XIE Xian-hong,LI Lan-qiang.A class of two-weight and three-weight linear codes and their duals[EB/OL].[2016-11-20].https://arxiv.org/abs/1611.06458v1.2016.

[16] WANG Qiu-yan,DING Ke-lan,LIN Dong-dai,et al.A kind of three-weight linear codes[J].CryptographyandCommunications,2017,9(3):315.

[17] YANG Shu-di,YAO Zheng-an.Complete weight enumerators of a family of three-weight linear codes[J].DesignsCodes&Cryptography,2017,82(3):663.

[18] YANG Shu-di,YAO Zheng-an,ZHAO Chang-an.A class of three-weight linear codes and their complete weight enumerators[J].JournalCryptographyandCommunications,2017,9(1):133.

[19] WANG Qiu-yan,DING Ke-lan,XUE Rui.Binary linear codes with two weights[J].IEEECommunicationsLetters,2015,19(7):1097.

[20] ZHOU Zheng-chun,DING Cun-sheng.A class of three-weight cyclic codes[J].FiniteFields&TheirApplications,2013,25(10):79.

[21] IRELAND K,ROSEN M.AClassicalIntroductiontoModernNumberTheory[M].Singapore:World Scientific,2003.

[22] BERNDT B C,EVANS R J,WILLIAMS K S.GaussandJacobiSums[M].Hoboken:Wiley,1998:75.

[23] DING Cun-sheng,YANG Jing.Hamming weights in irreducible cyclic codes [J].DiscreteMathematics,2013,313(4):434.

[24] COULTER R S.Further evaluations of Weil sums[J].ActaArithmetica,1998,86(4):217.