L-拓扑空间中的S1-连通性

潘 伟，徐振国

(1.牡丹江师范学院 数学科学学院，黑龙江 牡丹江 157011；2.国家科技基础条件平台中心，北京 100862)

0 引言

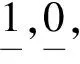
利用半开L-集和半闭L-集在L-空间中引入S1-连通性，如一般拓扑学中的连通性一样，它也具有许多理想的性质.特别地，著名的樊畿定理对于S1-连通性也成立.此外，还讨论了连通性和S1-连通性之间的关系.

引理1[3]设A,B∈LX且AB，如果1∈J(L)，则A′∨B≠1.

定义1[1]设(X,τ)是L-拓扑空间，G∈LX，则

(1)G称为半开L-集，如果G≤cl(int(G))；

(2)G称为半闭L-集，如果int(cl(G))≤G.

定义2[1]设(X,τ)是L-拓扑空间，G∈LX，定义

intS(G)=∨{D∈LX|D≤G,D是半开的}；

clS(G)=∧{D∈LX|D≥G,D是半闭的}.

1 S1-连通性

本节借助于S-分离L-集来研究S1-连通性.

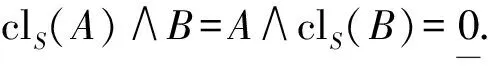
定理1设(X,τ)是L-拓扑空间且A,B∈LX，如果A和B是S-分离的且C≤A,D≤B，那么C和D同样是S-分离的.

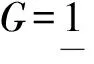
定理2设(X,τ)是L-拓扑空间且G∈LX，则下列情况等价：

(1)G是S1-连通的；

(2)不存在2个半闭L-集A,B，使得

(3)不存在2个半闭L-集A,B，使得

证明(1)⟹(2).假设G是S1-连通的且存在2个半闭L-集A,B使得

(2)⟹(3).假设存在2个半闭L-集A,B使得GA,G则事实上，如果那么由(A∨B)∧G=(A∧G)∨(B∧G)=G可知B∧G=G，这说明G≤B，这与GB相矛盾.同理这又与(2)矛盾.

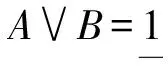
定理3设(X,τ)是L-拓扑空间，G∈LX,则下列结论等价：

(1)G是S1-连通的；

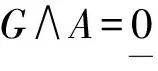
(3)如果A,B∈LX是S-分离的且G≤A∨B，那么G≤A或G≤B.

推论2J(LX)中每个元是S1-连通的.

定理4设(X,τ)是L-拓扑空间且G是S1-连通的，如果G≤H≤clS(G)，那么H是S1-连通的.

证明假设H不是S1-连通的，则存在2个半闭L-集A和B使得

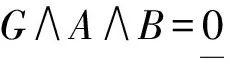
定理5设(X,τ)是L-拓扑空间，G和H都是S1-连通的，如果G和H不是S-分离的，则G∨H是S1-连通的.

证明假设G∨H不是S1-连通的,则存在2个半闭L-集A,B使得

由G∨HA有GA或HA.如果GA,那么由G的S1-连通性有G≤B.所以HB,H≤A.这表明于是类似地，这表明G和H是S-分离的，矛盾. 】

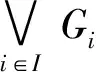
所以存在r,s∈I使得

这说明Gr∨Gs∨Gj不是S1-连通的.由定理5得到矛盾. 】

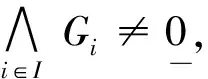
定理7设(X,τ)是L-拓扑空间且G∈LX,则G是S1-连通的当且仅当对G中任意2个非零的∨-既约元a,b,存在S1-连通的L-集H,使得a,b≤H≤G.

证明必要性是明显的，下面证充分性.假设G在(X,τ)中不是S1-连通的,则存在2个半闭L-集A,B∈LX，使得GA,G取两个非零的∨-既约元a,b≤G使得aA,bB.设H是S1-连通的L-集且满足a,b≤H≤G,则有HA,H这表明H不是S1-连通的，矛盾. 】

证明假设f→(G)在(Y,τ2)中不是S1-连通的，则存在2个半闭L-集A,B∈MY使得f→(G)A,f→(G)B,f→(G)所以Gf←(A),G这表明G不是S1-连通的，矛盾.于是f→(G)在(Y,τ2)也是S1连通的. 】

下面将樊畿定理推广到L-拓扑空间.文献[4]引入了远域映射的概念，类似地，给出下述定义.

证明⟸.假设G不是S1-连通的,则存在2个半闭L-集A,B∈LX使得

取a,b∈J(G)使得a≤A和b≤B.因为对于J(G)中任意有限个元x1=a,x2,…,xn=b,xi≤A和xi≤B(i=1,2,…,n)有且只有一个是真的，所以P(xi)=B或者P(xi)=A.但P(x1)=B,P(xn)=A，因此存在j(1≤j≤n-1)使得P(xj)=B，P(xj+1)=A.这表明G≤A∨B=P(xj)∨P(xj+1)，产生矛盾.

则对任意的c∈φ及任意的d∈ψ，有G≤P(c)∨P(d).设

A=∧{P(c)|c∈φ},B=∧{P(d)|d∈ψ},

则

显然，a和a可连接，于是a∈φ.因为a和b不可连接，所以b∈ψ，因此GA,GB.此外，明显有且由A,B的定义可知A,B是半闭L-集，这说明G不是S1-连通的，矛盾. 】

2 S1-连通性和连通性之间的关系

定理10在L-空间中，S1-连通的L-集是连通的L-集.

注1：定理9的逆不成立，这能从例1看出来.

例1设X={x1,x2},L={0,a,b,1},这里a′=a,b′=b,1′=0,0′=1;0

设(X,τ)是L-空间，这里τ={C(0,0),C(1,0),C(1,1)}，则C(0,1)是连通的L-集.下面证明C(0,1)不是S1-连通的.实际上，设Ω是所有半闭L-集之族，则

取半闭L-集C(0,a)和C(0,b)，由C(0,1)C(0,a)，C(0,1)可知C(0,1)不是S1-连通的.

参考文献:

[1] AZAD K K.On fuzzy semicontinuity,fuzzy almost continuity and fuzzy weakly continuity[J].JournalofMathematicalAnalysisandApplications,1981,82:14.

[2] CHANG C L.Fuzzy topological spaces[J].JournalofMathematicalAnalysisandApplications,1968,24:182.

[3] 王国民，史福贵.L-fuzzy空间的局部连通性[J].模糊系统与数学,1996,4:51.

[4] 史福贵，郑崇友.点式一致结构的刻画和格上度量化定理[J].数学学报,2002,45:1127.

[5] 刘念，伏文清，李生刚.L-预拓扑空间的强连通集和局部强连通L-预拓扑空间[J].模糊系统与数学，2013，27(3):181.

[6] 王国俊.L-fuzzy拓扑空间论[M].西安:陕西师范大学出版社,1988.