螺旋锥齿轮传动系统的时变参数调制及分析方法

冯美君，苏国营

(1.中国航发哈尔滨东安发动机有限公司，黑龙江 哈尔滨 150000；2.北京航空航天大学 机械工程及自动化学院，北京 100191)

在研究实际工程问题时，有很多问题的运动方程和数学模型可以用含有参数激励的非线性动力系统来描述，例如，在横浪或纵向波冲击下船舶的操纵稳定性和倾覆机理问题[1-3]，绳系卫星的振动与控制问题[4]，内燃机气门机构和离心摆式减振器的振动问题[5]，以及机械柔性结构系统的屈曲问题[6]等。而螺旋锥齿轮传动系统实质上是一个高维强参数周期系统，研究动力学特性本质上是对参数激励非线性系统的响应和稳定性分析，因而研究包含参数激励的非线性动力系统对解决实际工程问题具有十分重要的意义。

Bogoliubov和Mitroplsky等[7]用平均值的方法研究分析了Mathieu方程的渐近解，推动了含有参数激励非线性振动理论的发展。Sethna和Bajaj等[8-9]把分岔思想引入到非线性振动理论研究中，利用分岔思想研究含有参数激励的非线性动力系统的分岔，结果反馈良好。Malhotra和SriNamachchivaya等[10]研究分析了非线性可逆系统在非半单共振条件下的全局动力学问题。国内陈予恕等[11-13]利用L-S(Liapunov-Schmidt)方法和奇异性理论研究分析了含有参数激励的非线性动力系统的分岔。

上述各位学者的研究方法虽然各有所长，但在对类似螺旋锥齿轮的高维强参数周期系统的处理上仍然十分困难，现有的非线性振动理论对实际工程中具有周期运动特性传动系统的动态设计和分析有很多不足。

本文从状态转移矩阵、瞬态和稳态受迫响应等方面推导并构建了伪解析方法，对包含无限多频率成分的时变参数在规定频谱内进行连续阶跃调制，并进行了螺旋锥齿轮啮合振动的Hill-Meissner算例验证。

1 参数激励系统的受迫响应

对于N自由度广义参数激励系统的动力学问题，可由一个2N阶矩阵方程来描述：

(1)

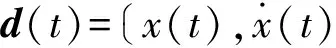
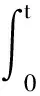
(2)

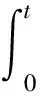
构建状态转移矩阵Φ(t,0)=W(t)W-1(0)，则式2可以转化为：

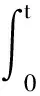
(3)

根据Floquet理论可知，时变周期为T的状态转移矩阵Φ(T,0)可转换为关于矩阵Γ的矩阵指数函数：

Φ(T,0)=eΓT

(4)

式中，Γ是一个固定矩阵。然后定义1个周期为T的矩阵为：

P(t)=Φ(t,0)e-ΓT

(5)

则系统任一时刻的状态转移矩阵及其可逆阵可以表述为：

Φ(t,0)=P(t)eΓ t
Φ-1(τ,0)=e-Γ τP-1(τ)

(6)

另外，系统的受迫响应解也可以由若干个余弦激励响应解构成，此时强迫激励项可表述为：

(7)

式中，r是余弦激励的幅值向量；ωf是强迫激励频率。将式7代入式3中可得：

(8)

由于Γ为对角化且其矩阵幂级数收敛，则式8中的矩阵指数函数应用Lagrange-Sylvester定理将变化成Jordan规范形的变换阵和Γ的特征值的函数，即：

e±Γ τ=Vdiag(eμit)V-1(i=1,2,…,2N)

(9)

式中，μi是矩阵Γ的特征值也即特征指数；V是特征向量矩阵。因为周期矩阵P(t)和P-1(t)都是连续且非奇异矩阵，因而求响应的伪闭合解时，可以使用傅里叶级数展开方法，因此可以表示为：

(10)

式中，ωp是参数激励频率，且ωp=2π/T。

至此，为消去式8中积分运算所需的变换都已经引入，可以得出最终的求解受迫响应的方程式。首先，将式9和式10代入式8中替换积分内部项；其次，将求和部分移出再展开积分；再将式9和式10代入上步，求解式中替换求和运算外部项，消去可乘的互逆矩阵，进行合并求和运算；最后，将每项中2个对角矩阵的相应元素相乘，可得：

(11)

式11就是参数激励系统在强迫激励下受迫响应的广义级数形式，右边第1项表示稳定响应部分，第2项表示瞬态响应部分。

如果系统是稳定的，则矩阵Γ或Floquet指数μ的特征值具有全部负实数，随着时间的增加，受迫响应的瞬态部分将接近零；相反，如果任何Floquet指数具有正实数，则解的瞬态部分将发散到无穷大，这表明不稳定性。

本文中，计算状态转换矩阵的方法是将时间段划分为更小的子区间，假设每个子区间上的时间是恒定不变的，例如，将周期T分为n个刚度恒定的子区间，n个子区间终点对应的状态转移矩阵分别为Φ(t1,0)、Φ(t2,0)直至Φ(tn-1,0)、Φ(T,0)，则周期状态转移矩阵Φ(T,0)可以用子区间的状态转移矩阵合成，如下：

Φ(T,0)=Φ(t1,0)Φ(t2,t1)…Φ(T,tn-1)

(12)

另外，矩阵Γ和Φ(T,0)共享特征向量矩阵，且Φ(T,0)的特征值λi和Γ的特征值μi间存在关系μi=ln(λi)/T；因此，可以求得式11中特征指数μi和V矩阵。这样，式11实现了受迫响应的级数形式解析计算，是一种伪闭合解。

2 时变参数的连续阶跃调制

对于受迫响应的伪闭合解，其精度完全取决于周期矩阵的傅里叶级数展开和周期状态转移矩阵。

对周期矩阵的傅里叶级数展开，一般要求最大谐波次数对应的频率大于时变参数激励最高频率成分的2倍。当时变参数激励包含无限多频率成分或最大频率成分不可知时，应用离散谱分析可以确定其主要频率成分和幅值，进而选定合适的谐波次数以构建周期矩阵的傅里叶级数。

对采用周期分段法求得的时变刚度系统周期状态转移矩阵，其精度与周期分段数n以及时变刚度在各个段上的取值有关。最简单直接的时变刚度分段采样方法是根据其曲线的变化形式，取在每个子区间上的平均值；但这种采样往往包含无限多频率成分，造成的结果是在响应计算时P(t)傅里叶级数展开时会出现混叠效应，进而使式11出现失真。

针对时变刚度参数各个分段上的采样值进行连续阶跃调制[14]。时变参数的连续阶跃调制采样如图1所示。

图1 时变参数的连续阶跃调制采样

取时变刚度的采样值(如平均值)的指数展开傅里叶系数为Km，则调制后的时变参数可表示为：

(13)

阶跃调制后，时变参数在各个子区间上的采样值为：

(14)

则有：

(15)

且其指数展开的傅里叶系数满足：

(16)

另外，将式16代入式14，可将调制后时变参数在各个子区间上的采样值表示为有限项的和，可得连续阶跃调制后时变参数采集值的一般方程形式为：

(17)

3 含不规律时变参数的二自由度Hill-Meisssner方程

在航空事业中广泛应用的螺旋锥齿轮，其单齿啮合接触轨迹不能简单的简化为直线，且每个瞬时接触点的载荷呈不均匀性，其齿面几何形状还与机床加工调整参数有密切关系，这些因素的叠加使得螺旋锥齿轮啮合刚度呈现无规律的时变特性。不规律周期时变参数如图2所示。

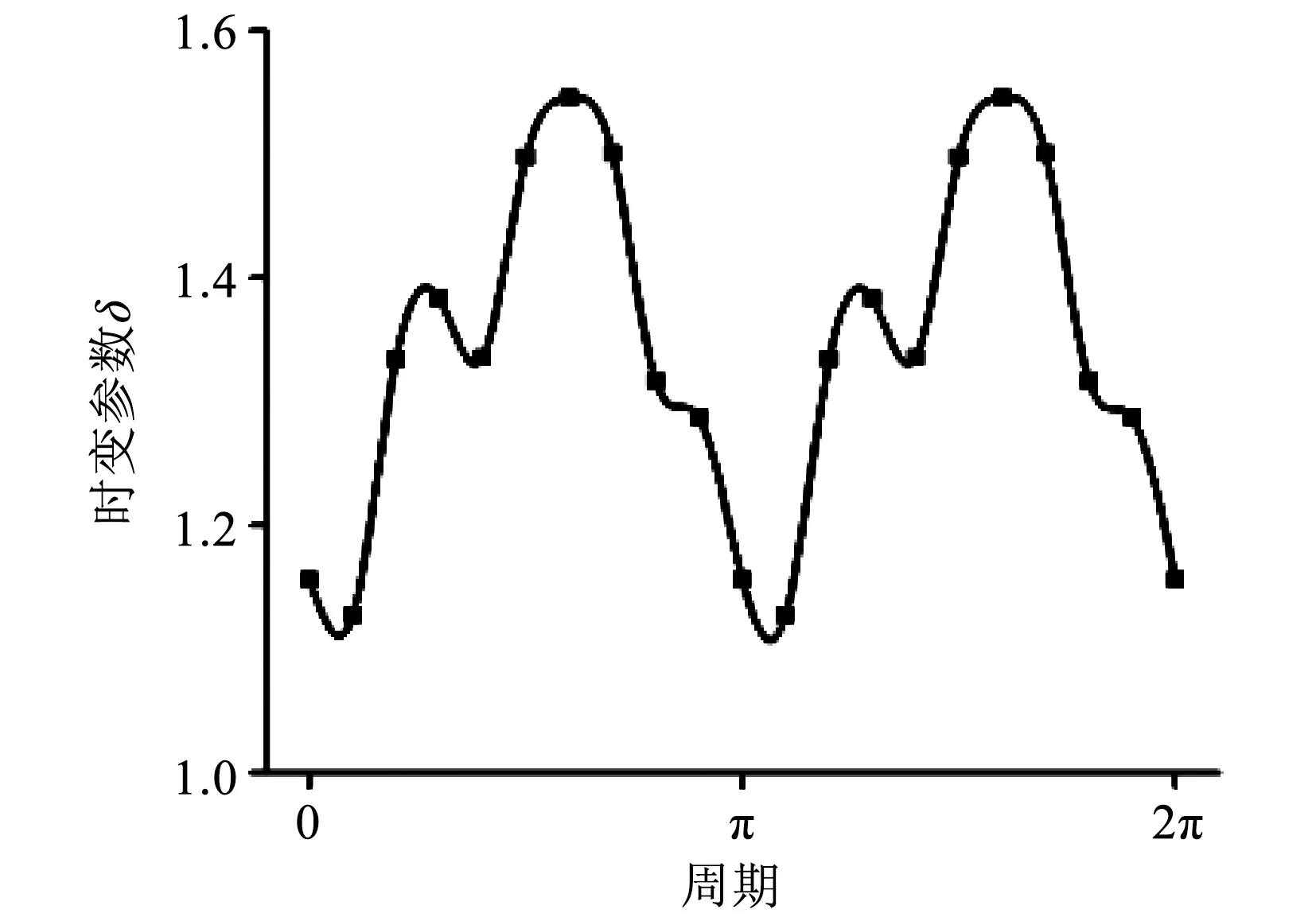
图2 不规律周期时变参数

考虑两端带支承刚度的二自由度螺旋锥齿轮传动系统动力学Hill方程：

(18)

将式10中周期矩阵傅里叶级数展开的谐波次数分别取32和64，将周期π划分成80个子区间，采用上述方法求解得到x2的受迫响应时间历程如图3所示。由图3可以看出，在含有余弦强迫激励和不规律时变参数情况下，该系统方程是稳定的，可以获得稳定周期解。

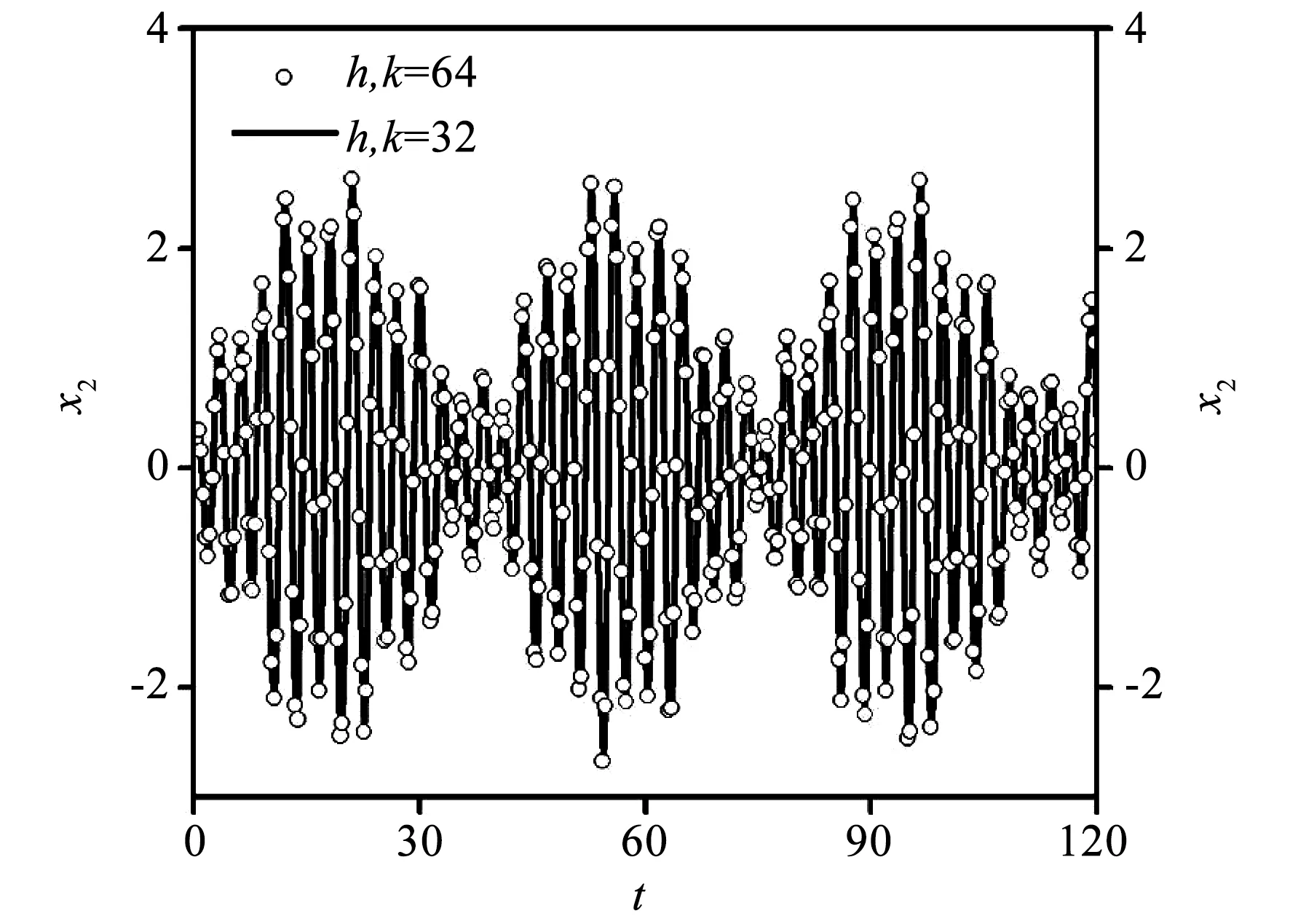
图3 含不规律时变参数方程稳定解的时间历程

若不考虑一端的支承刚度，则含时变参数刚度矩阵的右下角项由2+δ变为δ，重新求解得到模最大的Floquet乘子从(1,0)点穿出单位圆，出现鞍结分岔，x1和x2的失稳受迫响应相轨迹如图4所示，其中，x1为典型的极限环振动[15]。

图4 含不规律时变参数方程失稳解的相轨迹

4 结语

本文通过采用分段法解析计算了状态转移矩阵，对周期矩阵序列的傅里叶级数的开展和矩阵指数函数的Lagrange-Sylvester定理变换，获得了只依赖于状态转移矩阵的瞬态响应和稳态响应的伪闭合解。对包含无限多频率成分的时变参数在规定频谱内进行连续阶跃调制，避免了周期分段法计算状态转移矩阵引起的响应失真解。通过对包含不规律时变啮合刚度的螺旋锥齿轮啮合振动二自由度Hill方程的算例分析，验证了本文所建立数学分析方法的正确性和稳定性。对于航空事业中广泛应用的螺旋锥齿轮，可以有效分析其不规律时变啮合刚度引起的振动，为螺旋锥齿轮传动系统动力学研究建立了数学层面的基础。

[1] Sanchez N E, Nayfeh A H. Nonlinear rolling motions of ships in longitudinal waves[J]. International Shipbuilding Progress, 1990, 37(4): 247-272.

[2] Sanchez N E, Nayfeh A H. Prediction of bifurcations in a parametrically excited duffing oscillator[J]. International Journal of Non-Linear Mechanics, 1990, 25(2/3): 163-176.

[3] 陈予恕, 张伟. 现代数学和力学(MMM)VI：船舶横摇运动的全局分岔和混沌动力学[M]. 苏州: 苏州大学出版社, 1995.

[4] 彭建华, 刘延柱. 绳系卫星的混沌运动[J]. 上海交通大学学报, 1996, 30(11): 32-36.

[5] Zhang W, Ye M. Local and global bifurcations of valve mechanism[J]. Nonlinear Dynamics, 1994, 6(3): 301-316.

[6] 张清杰, 刘士光, 郑际嘉, 等. 结构动力屈曲研究进展[J]. 力学进展, 1993, 23(4): 530-538.

[7] Bogoliubov N N, Mitropolsky Y M. Asymptotic methods in the theory of nonlinear oscillations[M]. New York: Gordon and Breach, 1961.

[8] Sethna P R, Bajaj A K. Bifurcations in dynamical systems with internal resonances[J]. ASME Journal of Applied Mechanics, 1978, 45(4): 895-902.

[9] Bajaj A K, Shaw S W. Foreword[J]. Nonlinear Dynamics, 1993, 4(6): 527-530.

[10] Malhotra N, Sri Namachchivaya N. Global dynamics of parametrically excited nonlinear reversible systems with nonsemisimple 1∶1 resonance[J]. Physica D: Nonlinear Phenomena, 1995, 89(1/2): 43-70.

[11] 陈予恕, Langford W F. 非线性马休方程的亚谐分岔解及欧拉动弯曲问题[J]. 力学学报, 1988, 20(6): 522-532.

[12] 陈予恕. 非线性振动系统的分岔和混沌理论[M]. 北京: 高等教育出版社, 1993.

[13] 陈予恕, Han R P S. 现代工程非线性动力学的现状展望[J]. 力学与实践, 1995, 17(6): 11-19.

[14] Franks L E, Sandberg I W. An alternative approach to the realization of network transfer functions: The N-path filter[J]. Bell System Technical Journal, 1960, 39(5): 1321-1350.

[15] Schleimer J H, Stemmler M. Coding of information in limit cycle oscillators[J]. Physical Review Letters, 2009, 103(24): 248105.1-248105.4.