贵在比较，胜在迁移——以数量积为例谈解题教学

浙江省宁波市鄞州区姜山中学 (315191) 李 烽

波利亚曾说过：……教师能拿出一个有意义的但又不太复杂的题目，去帮助学生发掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域.在高中数学课堂教学中，我们在课前致力于优化学生的学习方案，课中努力提高课堂的学习效率，课后反思提升对数学问题的认知水平.其中一题多解、一题多变是一线教师常用的课堂组织形式.

1.问题的提出

在平面向量的复习中，一道数量积的练习解答不甚满意，通过面批，老师鼓励学生从多角度展开思考得到不同的解题体验，进而开设了一堂名为“三生三世，十里桃花”为主题的复习课.本文做一整理，以作抛砖引玉.

图1

2.教学过程

2.1 观当下，一题多解引思考

师：平面向量数量积集数形于一体，在解题中常与函数、不等式内容相结合，是高考和学考的热点考查内容.今天我们以本题为例，来谈一谈你在解题中的心路历程：即从何入手，遇到了哪些困难，你是怎样解决这些困难的？

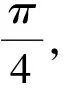
生2：这里还是有猜的成分，不好说明两线段乘积何时最大.我是从坐标入手的，转化后处理不等式问题.经过整理我们有以下几个方法：

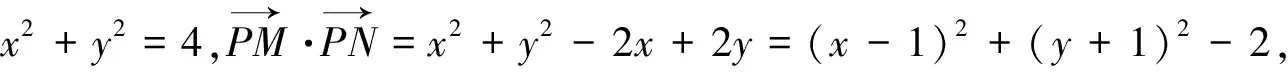
生3：这里的二个变量处理起来还是比较麻烦的，我从圆方程想到可设P(2cosθ,2sinθ)，参变量唯一，转化为三角函数值域问题，同样可得解.

生4：我一开始也是用坐标法来做的，但我发现在定圆问题中，抓住圆心和半径，利用投影能更快地解决问题.

师：以上几位同学分别从特值猜想、坐标代数论证、几何直观展示三个方向加以解决，解得都很好，展示了各位同学扎实的基本功.请同学们在整理以上方法的同时，着眼于策略的比较，议一议三个方向上的解法体会.

生1：特值猜想是选择填空中常用的方法，能提高解题的效率，帮我节省不少的时间，特别是在一类定值问题中常能起到秒杀的作用，但在取值范围问题中因停留于直觉判断，往往不够严谨造成失分.

生2：从几何意义角度解决问题清楚直观，但是在几何条件的寻找转化上常觉困难，特别是条件复杂的题感觉经常找不到门路.从数与形的表示中去寻求统一，坐标法给我们明确方向，距离、斜率、截距等几何属性是常见形式.

生3：我还是觉得坐标法更靠谱，建立合适坐标系，取值范围转化为函数问题，关键在于多元多参向一元单参的转变处理.各点坐标不明确的可考虑用唯一基底表示，用线性运算解决.

师：同学们都能结合自己的情况，谈了对这类题解法策略的理解，都说得很好.在平面向量最值问题的解决过程中我们注重坐标化、线性化、图形化的解题策略，注重方法的比较与归纳，定能有理想的收获.

2.2 赏过往，前世今生共比较

回溯过往，我们可以在高考、学考甚至于课本中找到本题的题源.

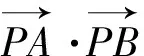
结合本课例题的多种解法，你对这三题会采取怎样的解题步骤？

生8：题1与例题类似，但突出了点在半圆上，我会用参数法设点，只要规定其中θ∈[0，π]即可.

生9：题2考查数量积的几何意义，从投影考虑显然此题只和弦AB的长度有关.

生10：题3各点坐标难以量化，我觉得用极化恒等式更简单，结合圆上动点到定点距离的几何属性可以迅速得到答案.

2.3 品变式，一题多变求余韵

对于此类三角形背景下的数量积问题，请大家展开讨论，还可以从哪些方面进行怎样的拓展变形.

比如逆向思维考虑：

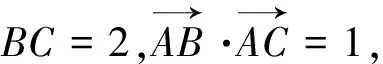
又如从动点的几何属性考虑：

2.4 悟题型，课堂小结归于一

请同学们从知识、方法、思想三个维度谈谈本节课的收获.

学生点评感悟，教师归纳统一.平面向量数量积的取值范围隐含函数的最值问题，坐标代数处理使其简单化，几何量图形转化实施使其直观化.

3.教学反思

例题教学要经过方法汇总——内化比较——外化迁移的过程，既要使其现形，更要使其入魂.通过方法的比较，使学生的思维得到锻炼，实现解题能力的提升.平面向量的数量积问题是高考和学考的一个热点，也是学生学习的一个难点.本课从基础问题出发，以一题多解、多变的教学方法，从特值猜想、坐标论证、数形结合三个视角，历经现在式、过去式、将来式三种变化，进行知识网络的整合，融合不等式、函数、解三角形等知识要点，有利于学生从联系的观点来理解和认识数学.

3.1 一题多解，方法的融合贵在比较

忽如一夜春风来，千树万树梨花开.教学的目的是使不同层次的学生的数学素养都得到一定的提高.在课堂的讨论交流中应逐步培养起自主探究的能力，先求百花争放，落实相关方法步骤的整理，再重梳理比较，在思路分析和方法比对中发现异同优劣，优化解题的策略，最后注重方法的总结与提升，使学生在解题活动中培养起归纳的习惯.其中方法间的比较是学习内化的过程：一要比较命题的背景和意图，“有什么求什么”；二要比较方法的过程与步骤，“怎么办怎样好”；三要比较效果和效率，“哪些可借鉴”.最终实现一种个人的解题习惯.

3.2 一题多解，方法的落实胜在迁移

千淘万漉虽辛苦，吹尽黄沙始现金.一题多解、一题多变在基本方法落实规范后，胜在及时准确地外化迁移.这要求我们对多解性方法进行必要地整理提炼，形成问题处理的经验.在适当时机能有序提取题设的条件，选择合适的方法才能提高解题的效率，炼得数学的真金.

好的例题教学应该是照亮学生解题的灯塔.立足于高观点，挖掘知识的内在结构，挖掘例题、习题的教学功能，才能领会知识中蕴涵的隐性思想，实现数学思想的渗透.既能玩味经久，又要入魂三分.