解析几何教学中发展运算素养的“五部曲”*
(363123)
数学运算是六大数学核心素养之一,也是当今学生较为弱化的一项重要能力.解析几何在高考中扮演了考查数学运算素养的重要角色.因其综合性强,题型多样,方法灵活,运算量大,数学思想丰富,学生普遍望题生畏.在高三综合测试中,解几题无一不是主要失分题.对这样的大众“难算”题,唯有提高运算素养方能标本兼治.巴金先生说:“学写作,只有写,才会写.”同样,攻克解几运算难关,只有算,才会算.以下,笔者以一道解几综合题的讲评与反思为例,从五个方面谈谈解析几何中如何发展数学运算素养,与同行交流探讨.
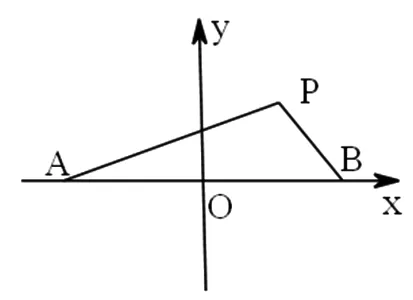
图1
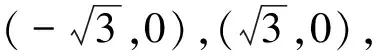
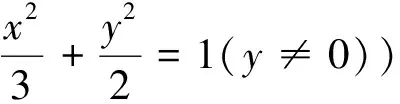
(2)设点P的轨迹为C,点M,N是轨迹C上不同于A,B的两点,且满足AP∥OM,BP∥ON,求证:△MON的面积为定值.
这是一道高考模拟题.第(2)小问很多学生求出点M,N的坐标后就止步了,难度系数仅为0.36.得分如此低,问题出在哪?
1.说困难,明晰运算障碍——山重水复疑无路
学生是学习的主人,复习课亦如此.经历解题碰壁,学生心中各有苦闷,讲评时要善于倾听学生的解题困惑,了解其知识缺陷、思维障碍、方法选择、运算困难,使讲评更具针对性.学生的主要思路如下:
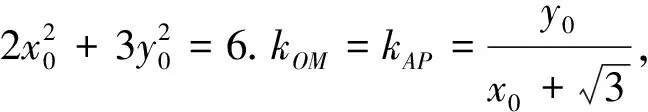
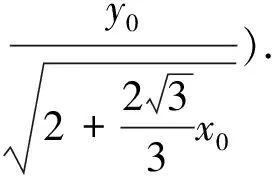
生2:(整体代换法2)由已知得kOM·kON=
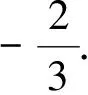
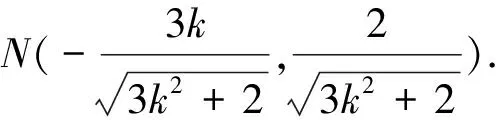
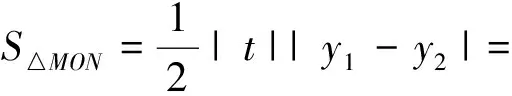
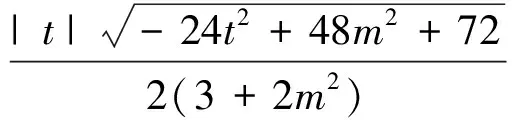
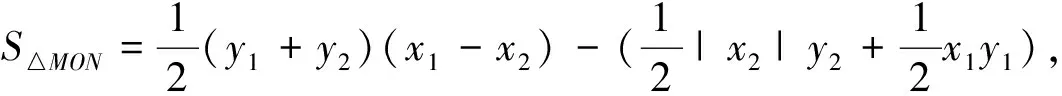
2.观路径,优化运算方法——柳暗花明又一村
解析几何题的特点是“想想容易,计算难”,特别是解题路径选择不当时,往往会卡死在繁琐的运算中.讲评时,应分析学生解题受阻的原因,引导其优化解题方法,顺应学生思路,帮助其逐步突破“藩篱”,让他享受到解题成功的快乐,以免陷入“屡战屡败”的畏难情绪.
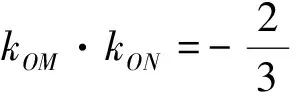
生5:(换底法)以OM为底,再求点N到OM的距离d,计算量就小多了……唉,是哦!一语惊醒“梦中人”,很多同学茅塞顿开.
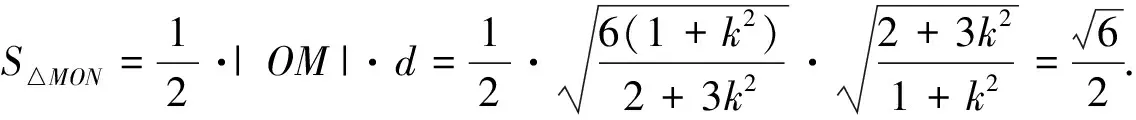
师:求得点M,N的坐标后,还有什么方法可表示出S△MON?
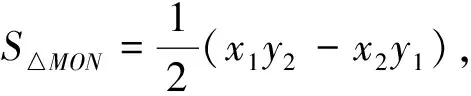
师:S△MON的表达式与生4的解法不谋而合呀,怎么她的做法不行呢?
引导同学再次观察方程“①,②,③”.几个优生发现:方程①②左右两边相乘,再将方程③代入,得(x1y2-x2y1)2=6.定值得求.
异曲同工啊!一个个障碍被跨越,同学们的思考热情高涨起来!
师:多字母运算时,要充分运用已知条件,用宽广的视野进行整体观察、整体运算.设直线方程及交点的坐标,但“设而不求”,是解直线和圆锥曲线问题的通法,生3的解法问题又出在哪?
至此,解题疑惑全打开.大家发现还是“换底法”最简单,它成功避开了将直线方程代入椭圆方程的运算,省去了“根与系数关系及曲线弦长”的繁琐计算.同学们感叹:条条大路通罗马,路径选择很重要!
若就此结束讲评,学生看清的只是原来模糊的一棵“树”,运算体会还是停留在解决单一问题的浅层水平.维果斯基的“最近发展区理论”认为,教学应着眼于学生的最近发展区,为学生提供带有难度的内容,调动学生的积极性,发挥其潜能,促进学生向更高水平发展.
3.探真相,形成运算程序——拨云见日现本质
师:△MON的面积为定值是必然还是巧合?对一般椭圆有类似性质吗?
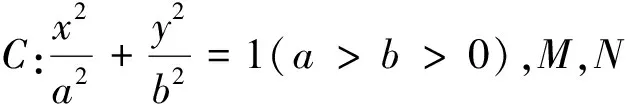
老师肯定了同学们的猜想.原来△MON的面积为定值是必然而非巧合.研究“一棵树”,发现“一片林”.大家思维飞扬,笔者于是乘胜追击.
追问1:如果延长MO,NO交椭圆于M′,N′,则四边形MNM′N′的面积是否为定值?若是,定值是多少?
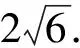
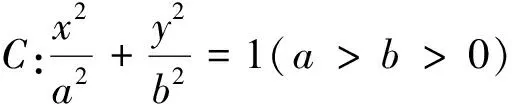
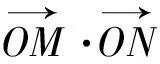
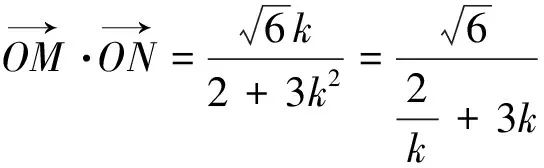
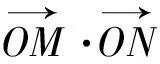
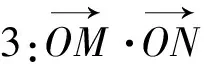
经过一番猜想、验证,同学们欣喜地发现:
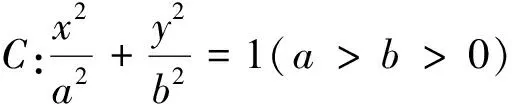
云雾散去,真相大白.打开一扇门,推开一扇窗:一个特殊结论的背后原来隐藏着“不能说的秘密”.解析几何高冷的形象瞬时可爱起来.3个追问,让学生对圆锥曲线的“定值、取值”问题思考更深入、思维更发散、视野更开阔,促进程序化思考问题的习惯的形成.
4.谈体会,树立运算信心——阳光总在风雨后
课后,笔者让学生对考试时的解题困惑及听讲后的感受做了简要书面小结,其丰富的内心体验,让人颇受启发.
生6:要灵活变通解题路径
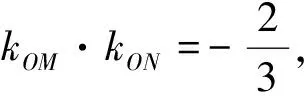
生7:不破楼兰终不还
生8:勇敢地算,不要怕繁长
做解几题时经常遇到较复杂的式子,不敢通分,导致化不到最简,无法算出结果.看过几道题后发觉,直线与椭圆有多个交点不确定时,大都可设直线方程解题,但要利用已知条件将点与点之间的关系建立起来,能整体同理代换最好,大大减少计算量.要勇敢地算,不要怕繁长的式子,最后一般都能约掉.
5.教后感,强化运算实践——绝知此事要躬行
解题具有实践性和探索性.波利亚说:“你想学会游泳,你就必须下水,你想成为解题高手,你就必须去解题.”弗里德曼特别强调:解题训练的心理学研究表明,学生在解题时不具备一般能力的基本原因,在于没有经常亲自动手进行分析,没有从中归纳出一般的运算方法及其理论根据.单墫教授认为,解题是一门实践性的学问,必须通过解题学解题.解析几何题的两大难点是:方法选择和运算化简.正如前面几位数学家所言,这两项素养只有在解题实践中摸索感悟、积累练就.因此,解析几何问题一定要舍得花时间让学生思考、运算和表达,让学生在自己解题、看人解题中学解题.解几复习教学中,认为让老师板书、学生计算很花时间,追求高容量、快节奏,重方法、轻过程的现象普遍存在;教师“一言堂”的讲评方式成常态.长此以往,复习教学广种薄收,助长了解几题成为学生啃不动的“老大难”问题.解析几何综合题虽然难度大,能力要求高,但复习教学中只要给学生“学会”的机会,还是能知难而进的.
第二,注重培养思维的灵活性.思维的灵活性是指转向的及时性,以及不过多地受思维定式的影响,善于从旧的模式或通常的制约条件中摆脱出来;是面对陌生情境能快速找到问题解决方法的良好思维品质.本课例中,大多数学生受“根与系数的关系”及“直线被曲线所截弦长”的定势影响,选择“设而不求法”和以MN为底求三角形的面积,导致陷入繁琐运算的沼泽.教学中,老师常将“直线与圆锥曲线问题”的解决程序化:①设直线方程,②将直线方程代入曲线方程,③用“根与系数的关系”求弦长或其它相关量.所以,学生在解题中形成思维定势、方法定势也在情理之中.其实,“换底法”和“图形割补法”更强调几何直观,注意从几何的角度分析与寻找问题解决的办法,而这也是解析几何问题的一个新导向.“几何属性”的恰当介入,突显了解析几何题“能力立意与多思少算”的命题特点.教师首先要跳出定势,设计不同类型的问题,引导学生在解题实践中体会、领悟解法的灵活性.
第三,不能贪量,而应求质.解析几何题虽千变万化,但在方法选择与计算策略上还是有相通之处.例如,什么时候宜正设直线方程:y=kx+t,什么时候宜反设直线方程:x=ky+t;涉及直线与曲线交点问题,通常运用韦达定理“设而不求”;双变量运算化简中,通常先化简再代入、尽量运用整体代换,如在本课例“设而不求法”中,若过早将“2t2=2m2+3”代入“y1+y2,y1·y2”,运算将非常复杂.在解析几何综合问题复习教学中,泛讲十题,不如练透一题:让学生用符合自己思维习惯的通法将题目解完整、做严谨;在多种方法的优劣比较中,感悟运算的优化、方法的选择;通过一个特殊结论,发现一片普通属性.“练透”的过程,同时也是扎实基础知识、训练思维能力、历练解题意志、丰富经验题感的过程.
罗增儒教授说:“基础知识要通过解题实践来消化;思维素质要通过解题实践来优化;解题方法要通过解题实践来强化.”同样,运算素养要通过解题实践来发展.解析几何教学中,应多为学生提供“思与算”的机会,让学生在解题实践中提升数学运算素养.
[1]罗增儒,数学解题学引论[M].西安:陕西师范大学出版社,2004.

