对一道教材习题的深入研讨

安徽省枞阳县第二中学 (246700) 许实宏安徽省枞阳县宏实中学 (246700) 江保兵

普通高中课程标准实验教材人教A版必修4习题3.2B组(P142)有这样一道习题:

问题1 设f(α)=(sinα)x+(cosα)x,x∈{n|n=2k,k∈N+}.利用三角变换，估计f(α)在x=2,4,6时的取值情况，进而对x取一般值时f(α)的取值范围作出一个猜想.

这道题语言简洁，短小精悍却寓义深刻，很值得深入研讨.本文先对x=2,4,6时的取值情况给予判定，然后提出猜想并结合主题，再对参数x的取值情况作进一步的讨论，最后从幂平均不等式的角度给予一个总结.

一、猜想与证明

证明：当x=2k,k∈N+时，f(α)=(sinα)x+(cosα)x≤(sinα)2+(cosα)2=1,当且仅当sinα=±1或cosα=±1时等号成立.

(1)当n=2,n=4时，结论显然成立；

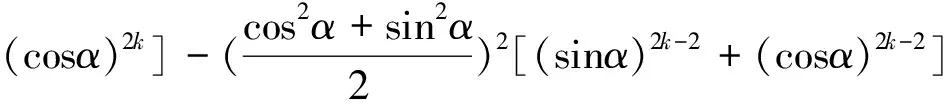
二．参数的变化

问题2 设f(α)=(sinα)2p+(cosα)2p,p∈{p|p≥1,p∈R},估计f(α)的取值范围.

问题3 设f(α)=(sinα)2p+(cosα)2p,p∈{p|p<1,p∈R},估计f(α)的取值范围.

问题4f(x)=xp+(1-x)p,p∈{p|p∈R,p≠0}，估计f(x)的取值范围.

三、幂平均不等式

首先介绍一下幂平均不等式：

问题5 设f(α)=(sinα)2p+(cosα)2p,p∈{p|p∈R,p≠0}，估计f(α)的取值范围.

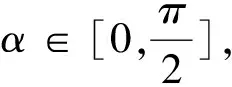
[1]单墫.我怎样解题.[M].上海：哈尔滨工业大学出版社，2013.

[2]波利亚.怎样解题.[M].上海：上海教育出版社，2001.

[3]罗增儒.数学解题学引论.[M].西安：陕西师范大学出版社，2008.