基于特征参数的冷水机组模型抗干扰性分析

赵琳，梁彩华，张小松



基于特征参数的冷水机组模型抗干扰性分析

赵琳，梁彩华，张小松

(东南大学 能源与环境学院，江苏 南京，210096)

基于将冷水机组未知的结构参数进行集总并由实测数据获取机组集总的结构参数(即特征参数)的建模方法，建立基于特征参数的冷水机组模型，并研究获取机组特征参数所需的实测数据中存在的测量误差对该建模方法及模型精度的影响规律。研究结果表明：当冷冻/冷却水流量、进/出口温度等机组实测值存在测量器具精度范围内的最大测量偏差时，冷水机组性能模拟值COP的相对误差小于2.5%，说明基于特征参数的冷水机组模型具有较高的抗干扰性。

测量误差；特征参数；冷水机组；抗干扰性

随着人们生活水平的提高，空调能耗在建筑能耗中所占的比重日益增加。据统计，空调能耗约占建筑总能耗的50%~70%[1−2]。常规的空调系统设备设计选型是以建筑的最大空调负荷为依据，而实测数据表明，机组在实际运行过程中有90%以上的时间处于部分负荷下运行[2−3]。对于以额定工况下运行最佳为目标而设计的空调系统，在部分负荷下运行时效率较低，可通过优化运行进一步提高系统效能的潜力。为实现冷水机组的优化控制，借助仿真模拟手段对冷水机组运行能效进行评估。首先需要对冷水机组各设备建立模型。冷水机组的仿真模拟方法有精确模型法和经验公式法。CHANG等[4]利用线性回归的方法并通过拟合经验公式建立了冷水机组的性能模型。LEE等[5]利用大量实验数据拟合得到冷水机组性能与水流量之间关系的多项式，并基于多项式建立了冷水机组在变流量工况下的性能模型。蒋小强等[6−9]采用拟合经验公式建立了冷水机组仿真模型并通过实测数据得到拟合参数。以上模型均基于已知机组内部结构参数或经验公式建立。在实际情况中，冷水机组各部件具体结构参数获取困难且大量的全工况数据难以获取，使得依据各设备具体结构参数进行建模的精确建模法和依据大量实测数据进行建模的经验公式法都受到限制。针对2种方法存在的不足，本课题组提出1种在水冷冷水机组各部件结构参数未知的情况下，通过理论分析将系统所有未知的结构参数集总，并利用少量实测数据获得集总后的结构参数即特征参数(不同机组具有唯一特定的特征参数)的建模方法。该建模方法无需具体系统结构参数且仅需少量的实测数据便可获取机组的特征参数，从而实现冷水机组的高效建模。但在建模过程中，所采用的实测数据(如温度、流量等)在其实际测量过程中存在因测量器具的偏移而引起的测量误 差[10]，以此实测数据为依据所获得的特征参数将影响冷水机组模型的精度。为此，本文作者针对基于特征参数法建立的冷水机组模型，通过理论分析与实验验证，研究实测数据中所存在的测量误差对该冷水机组模型精度的影响规律，以便为基于特征参数的冷水机组建模方法的性能评估提供依据。

1 基于特征参数的冷水机组模型

在水冷冷水机组实际结构参数未知的情况下，通过理论分析的方法对冷水机组主要部件(蒸发器、冷凝器、压缩机和节流阀)进行建模，建立实现基于特征参数的冷水机组模型。

1.1 蒸发器模型

对蒸发器的换热过程做如下假设：1) 忽略蒸发器与外界的换热；2) 以算术平均温差作为蒸发器的总换热温差。蒸发器换热过程方程组如下：

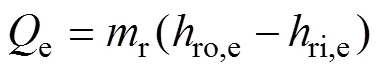
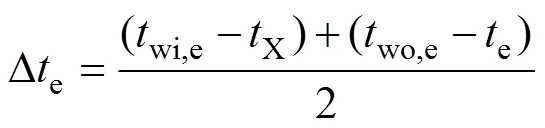
式中：e为蒸发器换热量；w,e为冷冻水流量；p,w为水比热容；wi,e为冷冻水进口温度；wo,e为冷冻水出口温度；r为制冷剂流量；ri,e为蒸发器入口焓；ro,e为蒸发器出口焓；e为蒸发器换热面积；Δe为蒸发器换热温差；e为蒸发温度；X为压缩机吸气温度，即蒸发器出口制冷剂温度；ee为蒸发器总热阻，ee与蒸发器结构参数有关，需要在未知结构参数的条件下建立蒸发器总热阻模型。

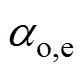
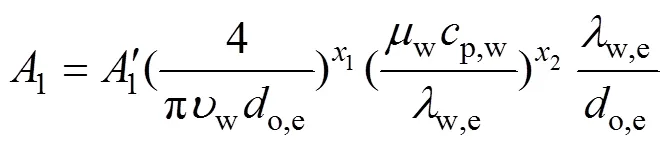
式中：1和2与蒸发器结构参数、制冷剂物性参数有关；1和2均为常系数。

制冷剂侧两相区和过热区的换热过程如下：

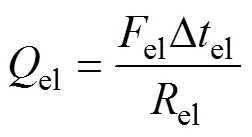
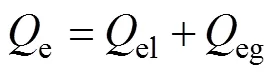
式中：el，el和Δel分别为两相区的换热量、换热面积与换热温差；eg，eg和Δeg分别为过热区的换热量、换热面积与换热温差；el和eg分别为蒸发器两相区和过热区的热阻；i,e为蒸发器管内径；m,e为蒸发器管公称直径；t,e为蒸发器管壁导热率。将式(6)~(15)并代入式(3)可得

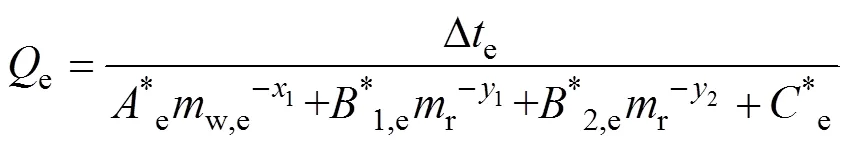
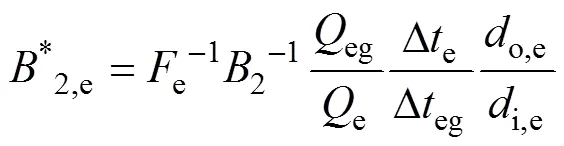
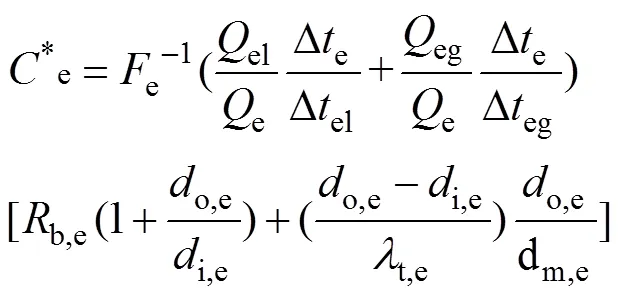
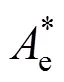
1.2 冷凝器模型

对冷凝器的换热过程作如下假设：1) 忽略换热器与外界的换热； 2) 以算术平均温差作为冷凝器的总换热温差。建立冷凝器总热阻模型的原理与蒸发器类似，可得如下冷凝器模型：

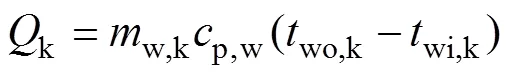
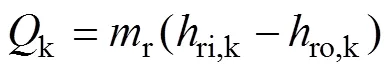
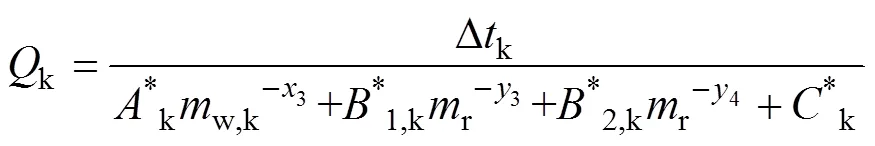
1.3 压缩机模型

假设忽略压缩机与外界的换热且压缩机效率及多变指数为常量，建立如下压缩机模型：

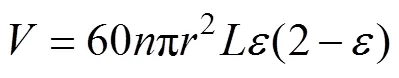
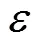
1.4 节流阀模型

假设节流前后制冷剂焓值不变，建立节流阀模型如下：

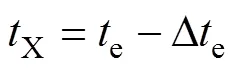
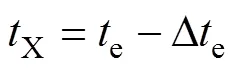
式中：ro,k为节流阀入口焓；ri,e为节流阀出口焓；Δe为过热度；Δk为过冷度。

2 冷水机组模型抗干扰性分析

在实际测量中，因测量器具偏移而引起的测量误差影响了测量准确度[10]，从而对以实测数据和基于特征参数的冷水机组模型为依据所获得的特征参数和性能评估参数产生影响。因此，研究实测数据中测量误差的存在对通过该模型所获得的特征参数和性能评估参数的影响(即对该模型进行抗干扰性分析)具有重要意义。在本文作者所建立的冷水机组模型中，所需获取的特征参数为蒸发器模型参数和冷凝器模型参数，而冷凝器模型与蒸发器模型结构相似，故只需对蒸发器模型进行抗干扰性分析。式(16)可转换为下列四元一次方程：

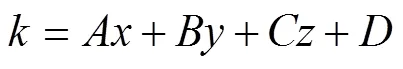
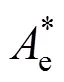
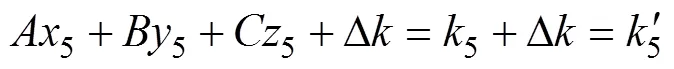
由式(37)可知：通过该蒸发器模型求取的模拟值不受测量误差的影响，与同工况下的实测值相等，故该蒸发器模型对于测量误差具有较高的抗干扰性能。同理，对于基于特征参数的冷凝器模型，因其模型参数的获取及模型结构形式与蒸发器模型类似，故该冷凝器模型对于测量误差也具有较高的抗干扰性能。综上所述，对由蒸发器模型参数和冷凝器模型参数确定的冷水机组模型对测量误差具有较高的抗干扰性能。

3 冷水机组模型抗干扰性实验验证

3.1 实验系统

空调系统实验装置示意图如图1所示。冷水机组采用转子式压缩机，蒸发器与冷凝器均为板式换热器，节流装置为热力膨胀阀，采用R22制冷剂。实验中，温度采用PT100铂电阻温度传感器测量，测量范围为−200~500 ℃，最大测量误差为±0.25 ℃。流量测量采用液体涡轮流量计，其满度流量为6 m³/h，精度为1.0%。系统数据采集采用Agilent数据采集仪。

图1 空调系统实验装置示意图

3.2 冷水机组模型参数的确定

式(16)和式(23)中的各模型参数通过实测数据获得。换热器换热系数的经验公式(见式(5))及1，1和2的值已知，因此，只需4组工况的实测数据即可得到4个模型参数。实验设定冷冻水回水温度为7.4 ℃，冷却水回水温度为26.5 ℃，冷冻水流量分别为0.4，0.5，0.6和0.7 kg/s，冷却水流量分别为0.6，0.7，0.8和0.9 kg/s，通过上面8种工况的实测数据可分别求得蒸发器模型和冷凝器模型的模型参数。

本文在实测值的基础上，用添加测量误差(各测量仪器的最大测量误差)的方式来模拟实际过程中因测量器具偏移产生的测量误差，将实测值和加有测量误差的数据分别代入模型中，求得对应的模型参数，即可获得对应的基于特征参数的冷水机组模型。

3.3 有关冷水机组模型精度的数据分析

为验证通过基于特征参数的冷水机组模型的精度和抗干扰性，另外测试10种随机工况，将其代入已确定的冷水机组模型中求取所需模拟值。

表1所示为10种随机工况的测试设定值、冷水机组性能模拟值COP及其相对误差。由表1可知：当压缩机频率在50~90 Hz之间变动时，机组COP随着压缩机频率的升高而降低，这是因为随着频率的升高，压缩机输入功率和制冷量都随之增大，由于输入功率的增加程度高于制冷量增加程度，故机组COP逐渐降低。COP最大相对误差出现在随机工况1处，为8.144%。由此可见，本文作者所建立的冷水机组模型具有较高精度。

3.4 有关冷水机组模型抗干扰性的数据分析

1) 通过实测值求得的模型参数及模拟值，表示为A组。液体涡轮流量计的最大流量测量误差为0.017 kg/s，对冷冻水流量添加最大测量误差∆w,e=0.017 kg/s，其余测量值不变，通过这种扰动数据求得的模型参数及模拟值，表示为B组；对冷冻水流量添加最大负测量误差∆w,e=−0.017 kg/s，其余测量值不变，通过这种扰动数据求得的模型参数及模拟值，表示为C组。A/B组和A/C组的COP及相对误差如表2所示，蒸发换热量及其相对误差如表3所示，压缩机功率及相对误差如表4所示。

由表2~4可知：对冷冻水流量添加最大正(负)测量误差时，测量误差的存在对通过冷水机组模型所求得的COP、蒸发换热量和压缩机功率的影响很小。在实测值w,e存在最大测量相对误差4.5%的情况下，COP受测量误差的影响而产生的相对误差均小于0.5%，蒸发换热量和压缩机功率相对误差均小于1.0%。

2) 对冷冻水进口温度添加最大测量误差∆wi,e= 0.25 ℃，模拟值表示为D组。对冷冻水进口温度添加最大负值测量误差∆wi,e=−0.25 ℃，模拟值表示为E组。A/D组和A/E组COP及其相对误差如表5所示。由表5可知：当实测值wi,e存在最大测量相对误差3.5%时， COP受测量误差的影响而产生的相对误差均小于1.1%。

3) 对冷冻水出口温度添加最大测量误差∆wo,e= 0.25 ℃，模拟值表示为F组。对冷冻水出口温度添加最大负值测量误差∆wo,e=−0.25 ℃，模拟值表示为G组。A/F组和A/G组COP及其相对误差如表6所示。由表6可知：当实测值wo,e存在最大测量相对误差3.5%时，COP受测量误差的影响而产生的相对误差均小于1%。

表1 10种随机工况的测试设定值、COP及其相对误差

表2 A/B组和A/C组的COP及其相对误差

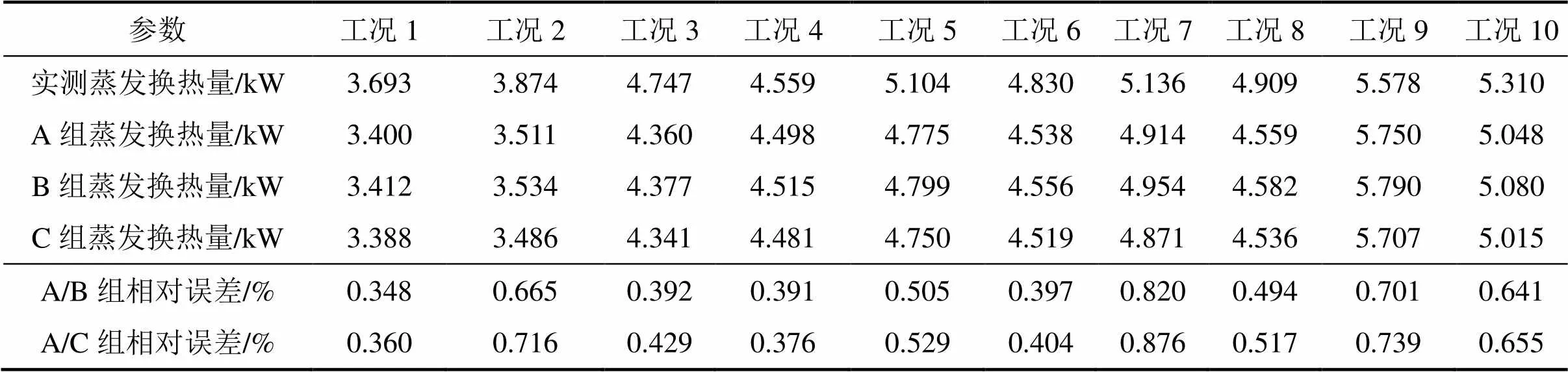
表3 A/B组和A/C组的蒸发换热量及其相对误差

4) 同时对冷冻水流量添加最大测量误差∆w,e=0.017 kg/s，冷冻水进(出)口温度添加最大测量误差∆wi,e=0.25 ℃，冷却水流量添加最大测量误差∆w,k=0.017 kg/s，冷却水进(出)口温度添加最大测量误差∆wi,k=0.25 ℃，模拟值表示为H组。对上述6种数据同时添加最大负值测量误差，模拟值表示为I组。则A/H组和A/I组COP及其相对误差如表7所示。由表7可知：在6种实测值同时存在最大相对误差时，COP受测量误差的影响而产生的相对误差均小于2.5%。

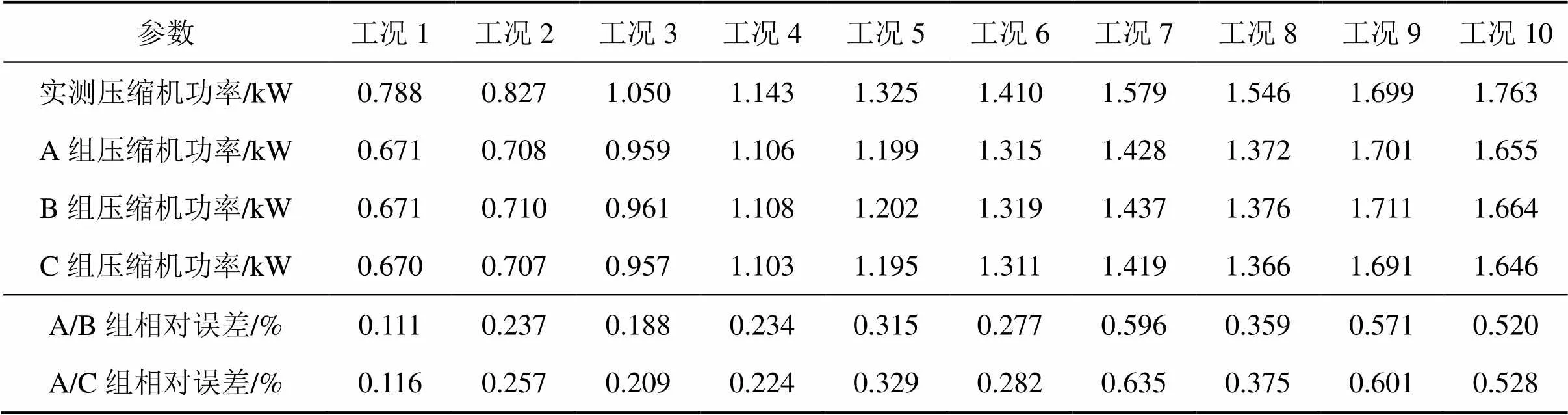
表4 A/B组和A/C组的压缩机功率及其相对误差

表5 A/D组和A/E组的COP及其相对误差

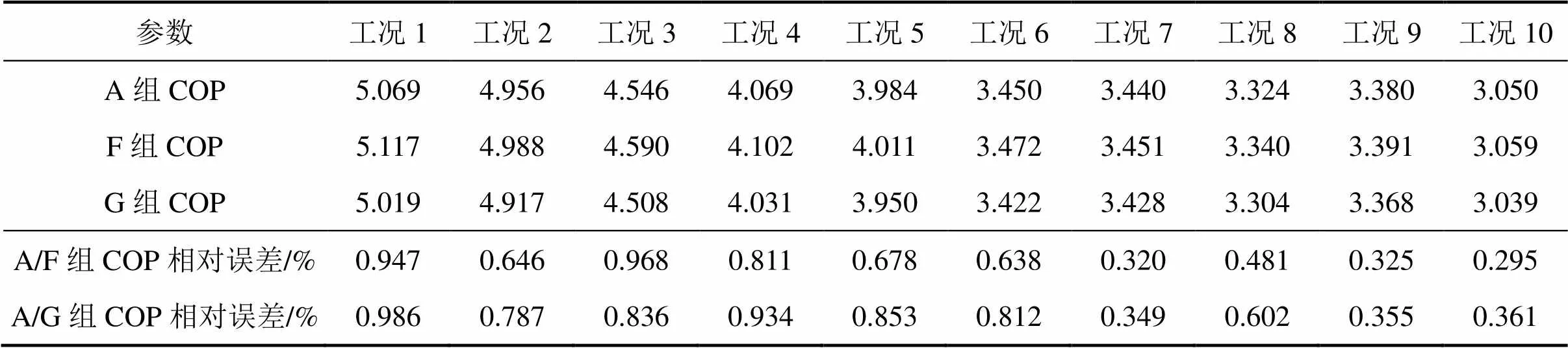
表6 A/F组和A/G组的COP及其相对误差

表7 A/H组和A/I组的COP及其相对误差

4 结论

1) 该冷水机组实测值与模拟值最大相对误差为8.144%，表明该模型具有较高的精度。

2) 在冷冻水流量或进出口温度的单一测量值存在测量误差的情况下，COP的相对误差均小于1.1%；在冷冻水流量、冷冻水进出口温度、冷却水流量、冷却水进出口温度同时存在测量误差(最大测量相对误差为4.5%)时，COP的相对误差均小于2.5%，说明该冷水机组模型相对于测量误差具有较强的抗干扰性。

[1] 陈小花. 我国建筑中央空调能耗现状及节能措施研究[J]. 科技信息, 2013(14): 241−242. CHEN Xiaohua. Study on energy consumption and energy saving measures of central air conditioning in China[J]. Scientific Information, 2013(14): 241−242.

[2] HERWANSULAIMAN M, IBRAHIM H, RUSLLIM MOHAMED M, et al. Differential search algorithm for optimal chiller loading for energy consumption reduction[J]. Australian Journal of Basic & Applied Sciences, 2014, 8(7): 92−98.

[3] SAIDUR R, HASANUZZAMAN M, MAHLIAT M I, et al. Chillers energy consumption, energy savings and mission analysis in an institutional buildings[J]. Energy, 2011, 36(8): 5233−5238.

[4] CHANG Yungchung, KONG Chai-Chee, CHEN Chien-Yi, et al. Verification method for energy saving of water chiller[J]. International Journal of Electronics Communications and Electrical Engineering, 2015, 4(2): 55−74.

[5] LEE T S, LIAO K Y, LU W C. Evaluation of the suitability of empirically-based models for predicting energy performance of centrifugal water chillers with variable chilled water flow[J]. Applied Energy, 2012, 93(S1): 583−595.

[6] 蒋小强, 龙惟定, 李敏. 制冷机房冷冻水和冷却水变流量解耦控制策略[J]. 重庆大学学报, 2010, 33(6): 6−12. JIANG Xiaoqiang, LONG Weiding, LI Min. Control strategy of variable flow between cooling water and chilled water in chilled plant[J]. Journal of Chongqing University, 2010, 33(6): 6−12.

[7] 蒋小强, 龙惟定, 王民, 等. 空调水系统变流量的运行特性[J]. 流体机械, 2010, 38(3): 71−75.JIANG Xiaoqiang, LONG Weiding, WANG Min, et al. Energy-efficiency performance with variable air-conditioning water flow rate[J]. Fluid Machinery, 2010, 38(3): 71−72.

[8] JIANG Xiaoqiang, LONG Weiding, WANG Min, et al. Optimum control strategy for all-variable speed chiller plant[J]. Journal of Central South University of Technology, 2011, 18(2): 573−579.

[9] CHAN K T, YU F W. Applying condensing-temperature control in air-cooled reciprocating water chillers for energy efficiency[J]. Applied Energy, 2002, 72(3):565-581.

[10] 林洪桦. 测量误差与不确定度评估[M]. 北京: 机械工业出版社, 2009: 360−400.LIN Hongye. Measurement error and uncertainty evaluation[M]. Beijing: Machinery Industry Press, 2009: 360−400.

[11] GASCONS M, BLANCO N, VIVES J, et al. Numerical implementation and experimental validation of a through the thickness temperature model for non-isothermal vacuum bagging infusion[J]. Journal of Reinforced Plastics and Composites, 2011, 30(18): 1557−1570.

[12] 江楚遥, 梁彩华, 张小松. 冷水机组变流量性能预测模型与实验研究[J]. 东南大学学报(自然科学版), 2014(2): 301−306. JIANG Chuyao, LIANG Caihua, ZHANG Xiaosong. Performance prediction model for chiller with variable water flow and its experiment validation[J]. Journal of Southeast University(Natural Science Edition), 2014, 44(2): 301−306.

[13] 江楚遥, 梁彩华, 范鹏杰, 等. 空调系统变冷冻水温性能实验与预测模拟[J]. 化工学报, 2014, 65(S2): 265−270. JIANG Chuyao, LIANG Caihua, FAN Pengjie, et al. Performance experiment and prediction simulation for air conditioning system with variable chilled water temperature[J]. CIESC Journal, 2014, 65(S2): 265−270.

[14] TANG Linghong, ZENG Min, WANG Qiuwang. Experimental and numerical investigation on air-side performance of fin-and-tube heat exchangers with various fin patterns[J]. Experimental Thermal and Fluid Science, 2009, 33(5): 818−827.

[15] Chen Changliang, Chang Y C, Chan T S. Applying smart models for energy saving in optimal chiller loading[J]. Energy & Buildings, 2014, 68: 364−371.

(编辑 伍锦花)

Anti-interference analysis of chiller model based on characteristic parameters

ZHAO Lin, LIANG Caihua, ZHANG Xiaosong

(School of Energy and Environment, Southeast University, Nanjing 210096, China)

A modeling method which lumps unknown structural parameters of chiller and gets the lumped parameters by measured data was used to build the chiller model. The influence of measurement error in measured data on the modeling method and accuracy of the model was studied. The results show that when the measured data of freezing/cooling water flow, the inlet/outlet temperature and other units have the maximum measurement error within the accuracy range of the measuring instrument, the relative error of simulated coefficient of performance (COP) is less than 2.5%, which indicates that the chiller model based on characteristic parameters has high anti-interference ability.

measurement error; characteristic parameters; chiller; anti-interference

10.11817/j.issn.1672-7207.2018.05.030

TK413.7+4

A

1672−7207(2018)05−1265−07

2017−05−28；

2017−06−29

国家自然科学基金资助项目(51676033)；“十二五”国家科技支撑计划项目(2015BAL02B01) (Project(51676033) supported by the National Natural Science Foundation of China; Project(2015BAL02B01) supported by National Science and Technology Pillar Program during the 12th “Five-year” Plan Period of China)

梁彩华，博士，教授，从事制冷空调系统性能优化、建筑环境与建筑节能等研究；E-mail: caihualiang @163.com