高碳耐磨球钢大方坯连铸过程凝固定律及在轻压下过程中的应用

安航航，包燕平，王敏，赵立华



高碳耐磨球钢大方坯连铸过程凝固定律及在轻压下过程中的应用

安航航1, 2，包燕平1，王敏1，赵立华2

(1. 北京科技大学 钢铁冶金新技术国家重点试验室，北京，100083；2. 北京科技大学 冶金与生态工程学院，北京，100083)

基于ANSYS软件建立310 mm×360 mm(长×宽)断面大方坯连铸过程二维凝固传热数学模型，通过窄面射钉试验及铸坯表面测温对模型的准确性进行验证，模拟不同碳质量分数高碳耐磨球钢大方坯宽面和窄面凝固坯壳的生长规律，将计算结果应用于轻压下过程中并进行现场试验。研究结果表明：模型能精确地获得不同工况下任意位置铸坯凝固坯壳的厚度分布、凝固终点位置及中心固相率。不同碳质量分数的高碳耐磨球钢具有相同的凝固规律：结晶器弯月面至二冷区出口，铸坯柱状晶区的凝固坯壳厚度与凝固时间的平方根呈线性关系，符合平方根定律，平方根定律的修正项与过热度有关；二冷区出口至凝固终点，相应铸坯等轴晶区凝固坯壳厚度与凝固时间的平方根呈非线性关系；根据凝固传热模型计算的高碳耐磨球钢BU铸坯中心固相率分布，结合轻压下合适的压下区间要求，拉速从0.43 m/min增加到0.52 m/min，轻压下可压区间增加，铸坯的中心碳偏析明显减少。

大方坯；凝固传热；数学模型；高碳耐磨球钢

在连铸生产过程中，大方坯高碳合金钢由于其具有高碳高合金的特性，其两相区宽且凝固时间长，铸坯易形成严重的中心疏松、中心缩孔和偏析缺陷。研究发现，铸坯中心偏析是影响钢材机械性能和使用性能的主要原因之一，如硬线钢的拉拔断裂以及轴承钢疲劳寿命下降[1−3]，而大量实践证明，对于大方坯生产高碳钢，凝固末端电磁搅拌和轻压下技术可明显改善铸坯中心疏松、降低中心线偏析和V型偏析，而凝固终点位置的准确判断对凝固末端电磁搅拌的安装位置和工艺及轻压下制度的制定和实施有极为重要的意义，凝固终点位置是凝固末端电磁搅拌(F−EMS)和轻压下(MSR)实施的先决条件[4]，目前，凝固终点位置主要是通过建立凝固传热数学模型，并根据射钉试验与测温试验对模型进行校核来精确预测。越来越多的大方坯连铸机同时配备凝固末端电磁搅拌技术和轻压下技术装备，掌握高碳钢大方坯凝固的影响规律，对最大程度发挥F−EMS和MSR的作用来控制高碳钢中心偏析有重要意义。研究人员针对大方坯高碳钢凝固规律研究得较多[5−7]，但专门针对同时配备F−EMS和MSR生产不同碳质量分数的高碳钢的研究较少[8]。热轧耐磨钢球具有硬度高、冲击韧性良好、成本低以及生产能耗低的优点。由于碳质量分数高且合金质量分数较低，在凝固过程中，固液两相区长，且凝固时间长，易形成较严重的中心缩孔和中心偏析(中心线偏析和V型偏析)，而针对高碳耐磨球用钢的研究较少。鉴于此，本文作者以同时装备F−EMS和MSR技术装备的断面长×宽为310 mm×360 mm的大方坯连铸机为研究对象，以高碳低合金耐磨球用钢BU，B6和B3为试验钢种，基于射钉试验以及测温试验验证大方坯二维非稳态凝固传热模型，得到任意工况下不同位置铸坯凝固坯壳厚度以及凝固终点位置，回归得宽面和窄面凝固坯壳厚度与凝固时间的数学关系，并根据凝固传热模型计算的高碳耐磨球钢BU铸坯中心固相率分布，通过调整拉速，重点研究轻压下过程中压下区间对高碳耐磨球钢中心碳偏析的影响。

1 大方坯凝固传热模型

大方坯二维非稳态凝固传热模型基于传热学原理，采用有限元法，利用ANSYS进行计算。

1.1 模型建立

研究的某厂大方坯连铸机的主要技术参数如下：断面长×宽分别为310 mm×360 mm和220 mm× 260 mm，弧形半径为12 m，冶金长度为26.2 m，结晶器有效长度为0.7 m，二冷各区长度(一区、二区、三区和四区)分别为0.35，1.17，1.77和4.04 m。以断面长×宽为310 mm×360 mm的大方坯为原型建立数学模型，基于大方坯在凝固过程的对称性，取其1/4断面为研究对象，以宽度方向为轴，厚度方向为轴，拉坯方向为轴，建立铸坯微元体。大方坯的凝固传热方程[6]为

建立二维数学模型时，在不影响计算结果的前提下，为简化方程及其边界条件，进行如下合理假设：

1) 忽略铸坯拉坯方向传热；

2) 对于液相穴内钢液对流，假设钢在液相区的导热系数大于固相区的导热系数，且随温度变化；

3) 各相的密度视为常数；

4) 忽略结晶器内与中间包内钢水的温度差，结晶器弯月面钢水温度与浇铸温度相同；

5) 结晶器内及二冷各区均匀冷却；

6) 将二冷区辊子传热与铸坯在二冷区辐射传热修正系数加入对流换热系数；

7) 大方坯内外弧传热量相同。

1.2 热物性参数的选择及处理

钢的固、液相线均采用JMat Pro软件计算，文中涉及的耐磨球用钢BU，B6和B3的典型成分及固、液相线温度如表1所示。

钢的密度在铸坯冷却过程中各相密度随温度变化，本模型中选择各钢固相区密度为7.4 t/m3，液相区密度为7.0 t/m3，两相区密度为7.2 t/m3。

本模型中凝固潜热采用等效比热容法进行处理，即以放大比热容的形式来减缓该区间内温度的变化速率，实现潜热释放的等效过程。经处理后两相区等效比热容eff的计算公式[9]为

固相率s采用下式[9]计算：

固相导热系数采用下式[9]计算：

式中：和为常数。

液相区的等效导热系数计算公式[9]为

式中：为常数，一般为1~4。

两相区的导热系数[10]计算公式为

式中：eff为两相区等效导热系数，W/(m·K)。

1.3 初始条件

当=0时，结晶器的钢水温度等于浇铸温度，即

1.4 边界条件

1) 铸坯中心。铸坯中心线两边为对称传热，中心点的边界条件可视为绝热边界，即

2) 固液界面。固液界面的表达式为

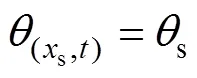
3) 铸坯表面。结晶器的表达式为

式中：s为铸坯表面热流密度，kW/m2；m为结晶器瞬时热流密度，kW/m2。

铸坯在结晶器内，采用平均热流计算：

表1 各钢种的典型成分及固、液相线温度

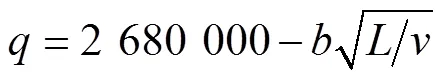
式中：为二冷段铸坯表面热流密度，W/m2；为所求瞬时热流位置距弯月面的距离，m；为拉速，m/min；m为结晶器的有效长度，m。

二冷区采用对流换热系数公式[9]计算

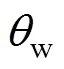
二冷各区换热系数公式如下。

足辊区：

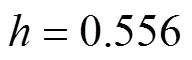
二冷段：

空冷区：

1.5 模型求解

连铸坯的凝固过程是非稳态传热过程，采用解析法求解非常困难，只能采用数值解，模型采用有限元法求其数值解。有限元法将连续的求解域离散为1组单元的组合体，用在每个单元内假设的近似函数来分片表示求解域上待求的未知场函数，近似函数通常由未知场函数及其导数在单元各节点的数值插值函数来表达，从而使连续的无限自由度问题变成离散的有限自由度问题，而数值计算法的实质是将一连续体离散化，用系列代数方程式代替偏微分方程式，计算得到温度场的近似解，本模型采用有限差分法对研究对象1/4 断面进行求解。

1.6 计算结果分析

图1所示为模型计算得到的BU钢在拉速为 0.48 m/min、过热度为27 ℃、比水量为0.18 L/kg时铸坯凝固过程的温度分布。图2所示为距结晶器弯月面3 m处铸坯横截面的温度云图，图3所示为铸坯宽面以及窄面的固相率分布。

由图1~3可以看出：模型能够精确反映任意位置铸坯的凝固情况，从而得任意位置整个横截面的凝固坯壳厚度分布。而铸坯窄面和宽面的凝固速率是不同的，窄面凝固较快，宽面凝固较慢，但最终的凝固终点相同。窄面方向的平均凝固速率约为7.31 mm/min，宽面方向的平均凝固速率约为6.62 mm/min。

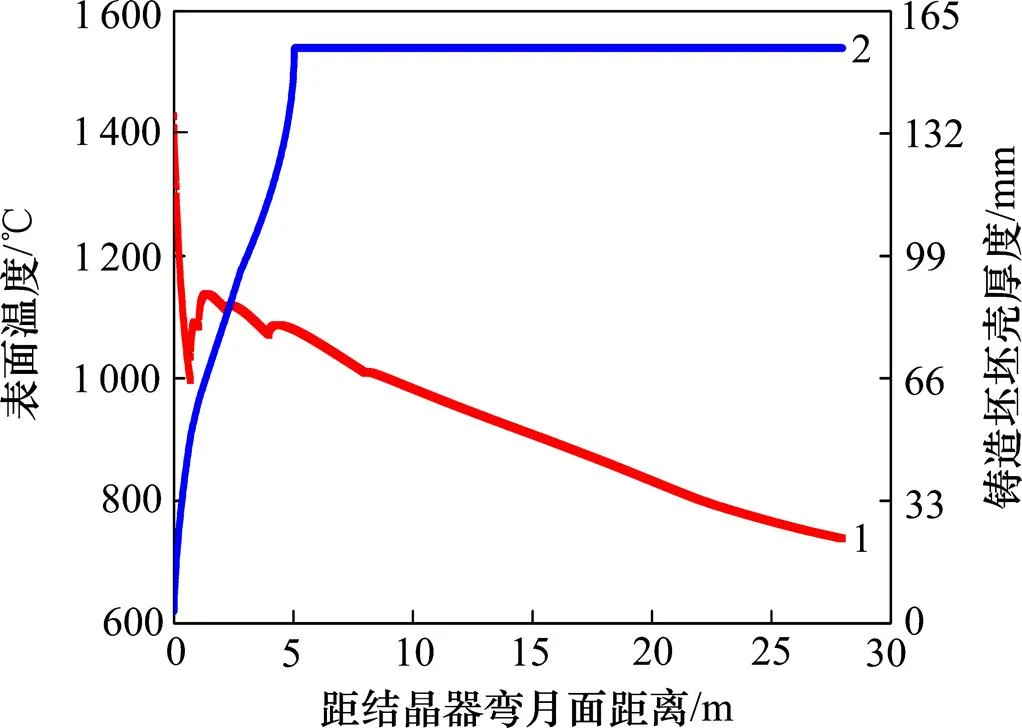
1—铸坯宽面表面温度；2—铸坯坯壳厚度。

图2 距结晶器弯月面3 m横截面的温度云图

2 模型验证

采用射钉试验以及测温试验对模型的准确性进行验证。

射钉试验是将装有示踪剂的低熔点硫化物(FeS)的钢钉(60Si2Mn)在连铸机不同位置处通过特制的射钉枪射入铸坯。待铸坯冷却后，切取含有射钉的试样，对试样进行刨光和打磨加工后显现出射钉的轮廓。由于硫化物熔点低，根据硫元素在固相区、两相区以及液相区扩散速率的不同，通过观察钉子的熔化状况以及硫元素的分布情况[10]，综合采用酸洗低倍法[11]和原位法[12]精确地获得射钉处的铸坯的凝固坯壳厚度、两相区以及液相区。

(a) 铸坯宽面；(b) 铸坯窄面

本次射钉试验选择为钢种为高碳耐磨球用钢BU，B6和B3，断面长×宽为310 mm×360 mm，射钉实际方案如表2所示。

以钢种BU、拉速为0.43 m/min、射钉位置距弯月面8.6 m获得的低倍以及原位分析结果为例，图4和图5所示分别为低倍法确定凝固坯壳厚度和原位法确定凝固坯壳厚度的结果。从图4和图5可知：固相区内钉子中的硫没有扩散到铸坯中，钉子保持原有的形状；在两相区内，钉子与铸坯之间界限模糊，因该区有液相存在，低熔点的硫局部扩散到铸坯中；在液相区内，钉子完全熔化，低熔点硫完全扩散到铸坯中。

在进行射钉试验的同时，分别在距弯月面8.6 m和13.5 m处利用红外测温仪测量铸坯宽面内弧表面中心处温度。测温过程中避开表面氧化渣处，待仪表显示温度稳定后，多次测温，取平均值。表2所示为射钉过程数值模拟计算的结果与实际测量结果的比较。从表2可知：本研究利用现场生产的参数，通过大方坯凝固传热数学模型，计算得到铸坯宽窄面中心的凝固坯壳厚度以及铸坯宽面的表面温度，并与射钉试验测得的实际窄面坯壳厚度以及实际测量的铸坯宽面的表面温度进行比较，使数学模型得到很好的验证，证明该模型能够合理反映任意位置处横截面的凝固坯壳厚度的分布情况，从而精确预测凝固终点的位置。

图4 低倍法确定凝固坯壳厚度

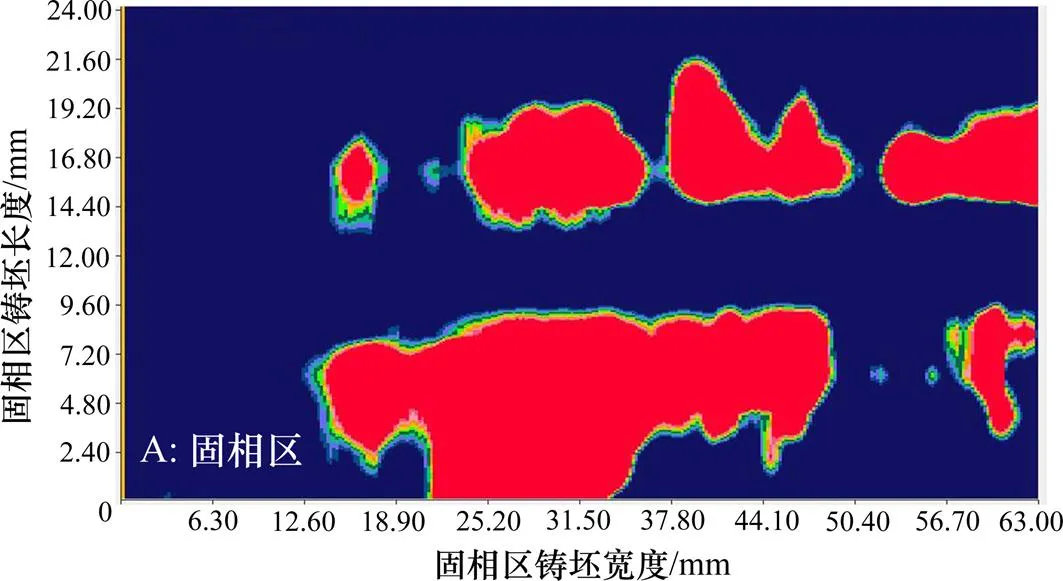
图5 原位法确定凝固坯壳厚度

3 高碳钢大方坯凝固规律的探讨

凝固过程中经典的平方根公式[13]如下：

式中：为凝固坯壳厚度，mm；为综合凝固系数，mm/min1/2；为凝固时间，min；s为射钉位置距结晶器弯月面的距离，m。

式(23)反映了一维顺序凝固坯壳长大的规律，板坯(边角部除外)与此符合很好，而大方坯为二维凝固，且在凝固末期存在加速凝固过程。

本次射钉试验的大方坯断面长×宽为310 mm× 360 mm，根据图3可知，铸坯宽面和窄面的凝固速率不同，一般大方坯射钉主要是在窄面中心处。以钢种BU为例，拉速为0.48 m/min，按照实测的窄面的凝固坯壳厚度，通过凝固平方根定律(式(23))计算不同射钉位置处的凝固坯壳厚度以及液相穴长度，计算结果如表3所示。

由表3可知：根据距弯月面8.6 m处坯壳厚度得出的凝固系数为18.4 mm/min2，代入式(23)计算距结晶器弯月面13.5 m处的坯壳厚度为97.8 mm，小于实际测量值25%。且计算的液相穴长度超过铸机的冶金长度30%，根据距结晶器弯月面13.5 m处的坯壳厚度得出凝固系数为28.2 mm/min2，距弯月面8.6 m处的坯壳厚度为102.9 mm，比实际测量值大32%，由此可见经典的凝固平方根公式已不能真实地反映大方坯整个凝固过程中窄面坯壳厚度与凝固时间的关系。根据表2可知，碳质量分数不同，拉速对液相穴长度以及影响也不同，很有必要对连铸高碳钢大方坯的凝固规律进行探讨。

结晶器内坯壳生长及传热比较复杂，本次研究从距弯月面1 m(结晶器下口)处开始研究坯壳的生长规律。图6所示为根据验证的凝固传热数学模型得到的BU钢宽面与窄面坯壳厚度与1/2的关系。由图6可看出：从结晶器弯月面至凝固终点，BU钢宽面和窄面中心坯壳厚度与凝固时间1/2的关系曲线非常相似，都在同一位置(即二冷区出口处，距弯月面8 m)出现拐点，并且拐点之前凝固曲线近似为直线，坯壳厚度与凝固时间1/2呈很好的线性关系，符合平方根定律，拐点之后曲线为非线性，这说明B6钢、B3钢与BU钢的凝固规律类似。下面以典型钢种BU在拉速为0.48 m/min，比水量为0.18 L/kg的情况为例讨论高碳钢在大方坯连铸过程中的凝固规律。

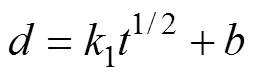
表2 模型参数计算结果与实际测量结果比较

表3 基于凝固平方根公式计算的凝固坯壳厚度与液相穴长度

1—BU−窄面；2—BU−宽面。

而从二冷区出口至凝固终点，凝固坯壳厚度与凝固时间1/2呈非线性关系，回归得到凝固坯壳厚度与凝固时间1/2的非线性关系式为：

图7所示为BU钢铸坯窄面与宽面坯壳厚度与凝固时间1/2的关系。由图7可看出：当BU钢拉速为0.48 m/min时，从结晶器弯月面下1 m到二冷出口(距结晶器弯月面8 m)，坯壳厚度与凝固时间1/2呈线性关系，宽面内外弧坯壳厚度与凝固时间1/2呈线性关系，坯壳厚度的区间为10~60 mm，窄面左右侧凝固坯壳厚度区间为17~65 mm。图8所示为射钉试验中的低倍试样。从图8可看到：宽面内弧柱状晶区以及柱状晶和等轴晶的混晶区的长度约为60 mm，窄面的约为65 mm，与凝固坯壳厚度的线性区间相符。由于结晶器电磁搅拌以及末端电磁搅拌的作用，加速了传热，打断了柱状晶，并扩大了等轴晶区，但实际混晶区可认为是在柱状晶的基础上形成的。平方根定律是根据单方向热传导公式推导出的，而柱状晶的生长方向理论上平行于热流方向。低倍观察表明柱状晶沿着垂直于模壁表面的单方向生长[13]，故大方坯连铸中内外弧坯壳在柱状晶区的生长符合平方根定律。这间接证明了状晶生长过程是单方向传热过程。

(a) 距弯月面1~8 m处宽面坯壳厚度；(b) 距弯月面1~8 m处窄面坯壳厚度；(c) 距弯月面8~20 m处窄面坯壳厚度；(d) 距弯月面8~20 m处宽面坯壳厚度

从距弯月面8 m处至凝固终点，坯壳厚度与凝固时间1/2呈非线性关系，铸坯中出现中心等轴晶区域，但由于等轴晶区的传热不能用单方向传热描述，因此，平方根定律不再有效。柱状晶生长时，液相的温度最高，而等轴晶生长时，晶体的温度最高，热流方向为晶体向周围钢液传递的方向，方向不唯一。

图8 射钉试验低倍试样

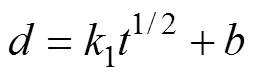
4 模型的应用

机械轻压下(MSR)是在连铸坯凝固末端附近施加机械应力以产生一定的压下量来阻碍富集偏析元素钢液的流动，从而消除中心偏析，同时补偿连铸坯的凝固收缩量以消除中心疏松[14]。轻压下技术主要的几个关键工艺参数包括压下区间、压下量、压下率和压下速率，而凝固终点位置的精确定位以及合理的压下位置是影响其冶金效果的前提条件。

压下区间是指压下量的作用区域，一般指在液相凝固终点与固相凝固终点之间，用相应拉矫机处铸坯的中心固相率s来表示，在0~1之间。本大方坯连铸机采用辊式静态轻压下，相比于其他连铸工艺参数，拉速对铸坯内凝固终点位置影响最大。鉴于此，在上述高碳钢大方坯凝固传热模型精确定位凝固终点的基础上，保持其他连铸工艺参数稳定，通过调整拉速，研究轻压下过程中压下区间对BU钢中心偏析的影响。表4所示为其他的连铸工艺参数，1~4号拉矫辊执行轻压下时辊缝与基准辊缝的差值分别为4，5，5和3 mm。表5所示为轻压下系统各拉矫机的位置，表6所示为不同拉速下基于凝固传热模型计算的1~4号拉矫辊位置铸坯的中心固相率s。

为确保不同浇铸工况下铸机设备及其工作状态一致，仅以该铸机第1流为试验流，以避免开浇和末浇工况不稳对试验结果的影响，在中间炉次过热度和其他参数稳定后，开浇10 min后提拉速取沿拉坯方向纵剖样和横样；采用钻孔法，钻头直径为4 mm，钻孔深度为8 mm，用碳硫分析仪对碳的成分进行分析。

表4 其他连铸工艺参数

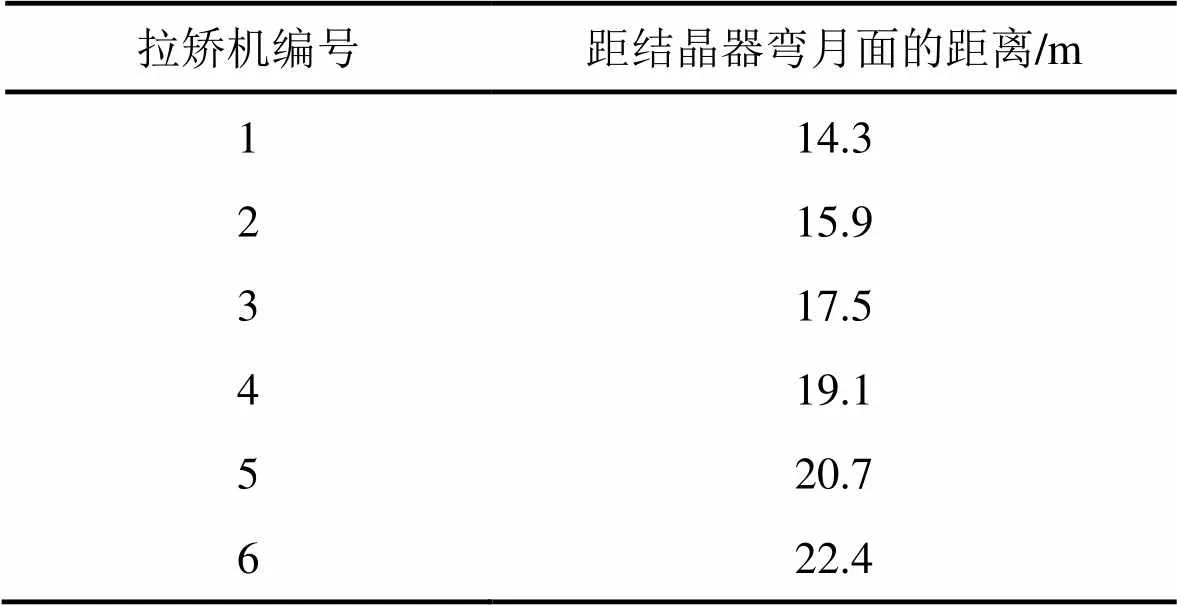
表5 轻压下系统各拉矫机的位置

表6 不同拉速下基于凝固传热模型计算的1~4号拉矫辊处铸坯的中心固相率fs

横截面试样取样位置如图9所示，在距中心1/8，1/4，1/2，3/4以及距铸坯表面5 mm钻孔取样，纵剖试样长度为400 mm，在中心线上沿拉坯方向每隔15 mm取1个点。

图9 横截面试样取样示意图

图10和图11所示分别为不同拉速下横截面铸坯内外弧中心线和纵剖面中心线碳偏析指数。由图10可知：当拉速从0.43 m/min提高到0.52 m/min时，横截面中心碳偏析指数(其值的定义为w/0，为取样点的碳质量分数，0为铸坯所在炉次中间包的碳质量分数)由1.06减小到0.95，反映铸坯内外弧取样点与中心的碳偏析指数波动的标准差由0.05降低到0.03。由图11可知：当拉速从0.43 m/min提高到0.52 m/min时，纵截面中心线碳偏析指数波动范围由0.83~1.17变为0.98~1.12。当拉速为0.52 m/min时，横截面中心碳偏析指数、内外弧取样点与中心的碳偏析指数的标准差最小，且纵剖面中心线碳偏析指数的波动范围最小，成分分布更均匀。

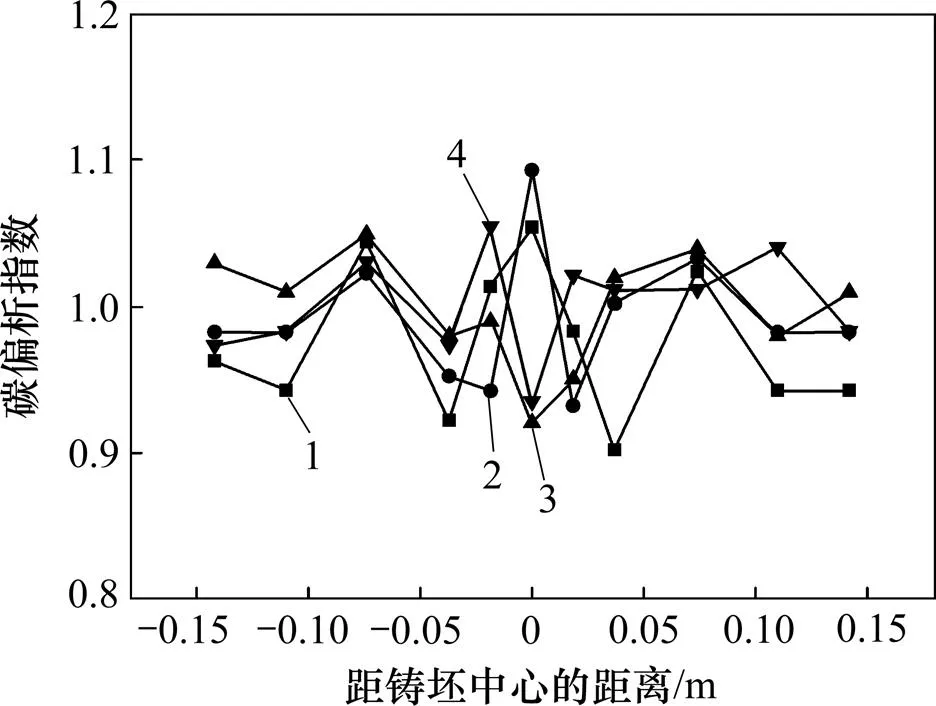
拉速/(m∙min−1)：1—0.43；2—0.48；3—0.50；4—0.52。

拉速/(m∙min−1)：1—0.43；2—0.48；3—0.50；4—0.52。

国内外多数研究表明，对于大方坯高碳钢，在铸坯的中心固相率为0.30~0.75或0.20~0.90[15]时进行轻压下可明显降低中心碳偏析指数，本文取0.30~0.75。从表6可知：当拉速为0.43 m/min时，凝固终点位置在1号和2号拉矫机之间，1号拉矫辊位置铸坯的中心固相率(s)为0.80，而2号拉矫辊位置铸坯已完全凝固，根据轻压下规则，采用1~4号拉矫辊进行压下时轻压下基本不起作用；当拉速提高到 0.52 m/min时，凝固终点在3号和4号拉矫机之间，1~4号拉矫辊处铸坯中心固相率(s)分别为0.34，0.50，0.74和1.00，根据轻压下规则，1~3号拉矫辊发挥了轻压下的作用。故当拉速为0.52 m/min时，可明显减少铸坯的中心碳偏析现象。

5 结论

1) 本文所提出的模型能精确地获得不同工况下任意位置大方坯高碳钢凝固坯壳的厚度分布、凝固终点位置及铸坯中心固相率。

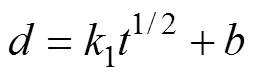
3) 大方坯宽面和窄面的坯壳生长规律相同，宽面坯壳生长速率比窄面的大，但凝固终点相同。

4) 根据凝固传热模型调整拉速优化轻压下压下区间，对于310 mm×360 mm的断面，在拉速为 0.52m/min，中心固相率为0.30~0.75时进行轻压下可明显减少高碳耐磨球用钢BU的中心偏析现象。

[1] 张游游, 刘建华, 苏晓峰, 等. BOF-LF-CC 生产SWRH82B硬线钢的洁净度研究[J]. 工程科学学报, 2016, 38(Suppl 1): 160−168. ZHANG Youyou, LIU Jianhua, SU Xiaofeng, et al. Cleanliness study of SWRH82B hard wire steel produced by BOF-LF-CC processes[J]. Chinese Journal of Engineering, 2016, 38(Suppl 1): 160−168.

[2] 逯志方, 张治广, 赵铮铮, 等. 过热度对轴承钢内部组织的影响[J]. 工程科学学报, 2016, 38(Suppl 1): 45−49. LU Zhifang, ZHANG Zhiguang, ZHAO Zhengzheng, et al. Influence of superheat on internal structure of the bearing steel[J]. Chinese Journal of Engineering, 2016, 38(Suppl 1): 45−49.

[3] 孙艳坤, 张威, 吴迪. 大断面轴承钢棒材超快速冷却工业化试验[J]. 钢铁研究学报, 2017, 29(3): 180−184. SUN Yankun, ZHANG Wei, WU Di. Industrial experiment of ultra-fast cooling for large-section bearing steel bar[J]. Journal of Iron and Steel Research, 2017, 29(3): 180−184.

[4] THOME R, HARSTE K. Principles of billet soft-reduction and consequences for continuous casting[J]. ISIJ International, 2006, 46(12): 1839−1844.

[5] SCHOLES A. Segregation in continuous casting[J]. Ironmaking and Steelmaking, 2005, 32(2): 101−108.

[6] 肖超, 张炯明, 罗衍昭, 等. 大方坯连铸过程凝固规律[J]. 北京科技大学学报, 2012, 34(9): 1011−1016. XIAO Chao, ZHANG Jiongming, LUO Yanzhao, et al. Solidification regularity of a bloom during continuous casting[J]. Journal of University of Science and Technology Beijing, 2012, 34(9): 1011−1016.

[7] 孙海波, 李烈军, 程晓文, 等. 大方坯末端电磁搅拌工艺参数优化与设计[J]. 炼钢, 2015, 31(4): 42−53. SUN Haibo, LI Liejun, CHENG Xiaowen, et al. Optimizing and designing the technology parameters of the F-EMS for the bloom continuous casting[J]. Steelmaking, 2015, 31(4): 42−53.

[8] 朱苗勇, 祭程. 连铸大方坯凝固末端重压下技术及应用[C]// 第十届中国钢铁年会暨第六届宝钢学术年会. 上海, 中国: 冶金工业出版社, 2015: 135−143. ZHU Miaoyong, JI Cheng. Heavy reduction technology and its application for bloom continuous casting process[C]// Proceedings of the 10th CSM Steel Congress & the 6th Baosteel Biennial Academic Conference. Shanghai, China: Metallurgical Industry Press, 2015: 135−143.

[9] ZENG Jie, CHEN Weiqing, WANG Guangshun, et al. Development and application of an off-line soft reduction model during continuous casting of high-carbon rectangular billet[J]. Metallurgical Research & Technology, 2015, 403(112): 1−9.

[10] 安航航, 韩传基，韩丽娜, 等. 大方坯连铸40Cr凝固特性及铸坯质量的研究[J]. 连铸, 2013(1): 36−40. AN Hanghang, HAN Chuanji，HAN Lina, et al. Solidification characteristics and slab quality of 40Cr of bloom caster[J]. Continuous Casting, 2013(1): 36−40.

[11] 王睿, 包燕平, 彭尊, 等. 圆坯连铸过程中坯壳生长规律[J]. 工程科学学报, 2015, 37(3): 301−306.WANG Rui, BAO Yanping, PENG Zun, et al. Shell growth of round blooms during continuous casting[J]. Chinese Journal of Engineering, 2015, 37(3): 301−306.

[12] 左晓剑, 杜申, 刘强, 等. 管线钢连铸板坯横截面元素的原位统计分布分析[J]. 冶金分析, 2017, 37(1): 1−7. ZUO Xiaojian, DU Shen, LIU Qiang, et al. Original position statistic distribution analysis of the elements in cross section of pipe line steel continuous casting slab[J]. Metallurgical Analysis, 2017, 37(1): 1−7.

[13] 蔡开科. 浇注与凝固[M]. 北京: 冶金工业出版社, 1987: 45−48. CAI Kaike. Casting and solidification[M]. Beijing: Metallurgical Industry Press, 1987: 45−48.

[14] JI Cheng, LUO Sen, ZHU Miaoyong. Analysis and application of soft reduction amount for bloom continuous casting process[J]. ISIJ International, 2014, 54(3): 504−510.

[15] THOME R, HARSTE K. Study on the design of the soft reduction unit of high-speed billet casters[J]. Steel Research International, 2004, 75(10): 693−700.

(编辑 刘锦伟)

Solidification regularity of high carbon wear-resistant ball steel in bloom continuous casting and its application in soft reduction process

AN Hanghang1, 2, BAO Yanping1, WANG Min1, ZHAO Lihua2

(1. State Key Laboratory of Advanced Metallurgy, University of Science and Technology Beijing, Beijing 100083, China;2. School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China)

A two-dimensional mathematical model of solidification and heat transfer for a bloom with the cross section of 310 mm×360 mm(length×width) was established with ANSYS software, which was verified by nail-shooting experiments in the narrow side of the bloom and surface temperature testing. The solidified shell growth law of high carbon wear-resistant ball steel with different carbon mass fractions in both wide and narrow side of the bloom was simulated based on the model. The results were also applied in the soft reduction process and the field experiments were carried out. The results show that the solidified shell thickness distribution of the bloom, the position of the solidification end point and the solid fraction in the core of the solidified strand under different working conditions can be accurately obtained by using this model at any fixed location along the casting direction. In addition, high carbon wear-resistant ball steels with different carbon mass fractions obey the same law of solidification: from the meniscus of the crystallizer to the secondary cooling zone export, the solidified shell thickness in the columnar crystal zone of the bloom and the square root of solidification time show a linear relationship, which fits the square root law．The correction term of the law is relevant to the superheat. However, from the secondary cooling zone export to the end of solidification, the relationship between solidified shell thickness in the equiaxed crystal zone of the bloom and the square root of solidification in the columnar crystal zone is non-linear. In accordance with the calculated solid fraction at the centerline of strand in wear resisting ball steel BU bloom by model of solidification and heat transfer, combined with reasonable soft reduction zone, the casting speed increases from 0.43 m/min to 0.52 m/min. Consequently, soft reduction zone is prolonged and the center carbon segregation on wear resisting ball steel BU is reduced obviously.

bloom; solidification and heat transfer; mathematical models; high carbon wear-resistant ball steel

10.11817/j.issn.1672-7207.2018.05.003

TF777.2

A

1672−7207(2018)05−1037−10

2017−05−31；

2017−07−11

国家自然科学基金资助项目(51404018)；钢铁冶金新技术国家重点试验室自主基金资助项目(41614014) (Project(51404018) supported by the National Natural Science Foundation of China; Project(41614014) supported by the Foundation of State Key Laboratory of Advanced Metallurgy)

包燕平，博士，教授，从事炼钢新工艺及高效连铸新技术研究；E-mail: baoyp @ustb.edu.cn