基于归一化互相关成像条件的GPR逆时偏移成像

陈德鹏，戴前伟，冯德山，王洪华，张彬



基于归一化互相关成像条件的GPR逆时偏移成像

陈德鹏1, 2, 3，戴前伟1, 2，冯德山1, 2，王洪华3，张彬1, 2

(1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083;2. 有色金属成矿预测与地质环境监测教育部重点实验室，湖南 长沙，410083；3. 桂林理工大学 地球科学学院，广西 桂林，541004)

针对基于零时刻成像条件的探地雷达(GPR)逆时偏移精度低、难以对复杂结构进行高精度成像的缺点，将归一化互相关成像条件应用于GPR叠前逆时偏移成像。从二维GPR电磁波方程出发，采用基于完全匹配层(PML)边界条件的时域有限单元法(FETD)模拟电磁波正向和逆向传播，采用归一化互相关成像条件获取叠前逆时偏移的偏移结果，将空间高通滤波用于压制互相关过程中产生的低频噪声，然后编制相应的GPR叠前逆时偏移程序。在此基础上，建立2个复杂的GPR模型，利用基于归一化互相关成像条件的GPR逆时偏移程序进行计算，并与基于零时刻成像条件的GPR逆时偏移剖面进行对比。研究结果表明：与基于零时刻成像条件的GPR逆时偏移剖面相比，基于归一化互相关成像条件的GPR叠前逆时偏移剖面能更清晰地反映异常体空间形态和内部结构信息，其分辨率和成像精度更高。

探地雷达；逆时偏移；归一化互相关成像条件；零时刻成像条件

探地雷达(ground penetrating radar, GPR)作为一种采用高频脉冲电磁波探测地下地质体结构及物性参数的重要浅部地球物理方法[1]，具有无损性、分辨率和效率均较高等优点，在工程与环境等领域得到广泛应用[2−4]。偏移是实测GPR数据向真实地下结构转换的最重要环节，偏移质量将直接影响后续解释的准确性。目前，常用的GPR偏移方法主要有Kirchhoff偏移 法[5]、频率−波数域偏移法[6]和逆时偏移法[7]等。在众多偏移方法中，逆时偏移方法具有精度高、相位准确、不受横向变速和高陡倾角影响、能够适应沿任意方向传播波场等优点，可更精准地将电磁波场归位到其真实位置，因此，得到越来越多研究者的广泛关注[8]。与弹性波逆时偏移类似，GPR逆时偏移根据不同的数据采集方式可采用不同的成像条件。目前，常用的GPR逆时偏移成像条件主要有零时刻成像条件、零延时互相关成像条件和归一化互相关成像条件。零时刻成像条件的基本原理是根据爆炸反射面模型，将地表接收的GPR数据进行逆时外推，接收波场外推至零时刻的结果即为逆时偏移成像剖面。目前，该成像条件主要用于等偏移距GPR数据逆时偏移处理。FISHER等[9]借鉴弹性波逆时偏移算法，将零时刻成像条件应用于GPR数据的逆时偏移成像。随后，LEUSCHEN等[10−14]对零时刻成像条件的GPR逆时偏移算法进行完善，并应用于实测数据处理。由于现有的商业GPR系统大都采用剖面法测量，因此，基于零时刻成像条件的逆时偏移算法被广泛应用于实测GPR数据处理。然而，采用剖面法测量时，偏移距较小，难以对高陡地层构造产生的反射波进行有效采集，因此，基于零时刻成像条件的GPR逆时偏移难以对复杂结构进行高精度成像。近年来，随着阵列天线GPR系统的成功研制和应用，多偏移距数据的快速采集成为可能，GPR叠前逆时偏移方法得到人们的重视。它以采集的多偏移距数据为基础，根据成像点的入射波到时和反射波到时相同的原理，计算源点正传电磁波场和接收点反传电磁波场的互相关，从而对地下复杂结构进行成像。朱尉强等[8, 15−16]将基于互相关成像条件的逆时偏移算法引入GPR数据处理，针对GPR电磁波的传播特点和介质特性对逆时偏移算法进行完善，能适应多天线或阵列天线观测模式。然而，现有的互相关成像条件应用于GPR叠前逆时偏移处理时，在发射源点附近会产生很强的低频噪声，并且深部结构的反射能量异常微弱。为此，CLAERBOUT等[17]根据弹性波逆时偏移算法提出了归一化互相关成像条件，其基本原理是利用源点电磁波场或接收点电磁波场对两者的互相关成像结果进行归一化。该成像条件可有效减弱发射源点附近的低频噪声，且大大加强深部结构的反射能量，目前被广泛应用于声波和弹性波逆时偏移成像。本文在借鉴前人逆时偏移理论基础上，将归一化互相关成像条件应用于GPR叠前逆时偏移成像。将时间域有限单元法(FETD)用于模拟电磁波正向和逆向传播过程，归一化互相关成像条件用于获取逆时偏移结果。设计2个复杂GPR模型，利用归一化互相关成像条件的逆时偏移算法进行计算，并与零时刻成像条件的逆时偏移结果进行对比。

1 GPR逆时偏移成像方法

GPR逆时偏移的基本原理是将地表采集的接收电磁波场在时间轴上进行逆向传播，当电磁波场逆推至零时刻时，所有反射波与绕射波的能量都回到最初被反射和绕射的空间位置，然后应用成像条件可获取最终的成像剖面。因此，GPR逆时偏移实现过程可分为以下3步：1) 在时间域进行源点电磁波场的正向传播；2) 在时间域进行接收点电磁波场逆时外推；3) 利用成像条件获得成像结果。其中，前2步可利用相同的数值模拟方法进行计算，本文采用基于三角形网格剖分的FETD来模拟电磁波的正向及逆时外推。

1.1 电磁波场正向传播及逆向外推

考虑二维地电模型的走向为轴，根据电磁波理论，TM模式下电场分量满足的波动方程为[18]

式中：E为方向电场强度(V/m)；，和0分别为介质的介电常数(F/m)、电导率(S/m)和真空磁导率(H/m)；为激励源函数。利用伽辽金有限元法可推导式(1)的有限元方程[18]为

其中：，′和分别为质量矩阵、阻尼矩阵和刚度矩阵，它们只与介质的物性参数和几何分布有关；为源向量。采用三角形网格对计算区域进行剖分(如图1所示，其中N和N分别为和方向的网格数)，每个矩形网格被2条对角线再剖分成4个三角形网格，以提高复杂GPR模型的正向与逆向电磁波场的计算精度。同时，在计算区域的外边界采用完全匹配层吸收边界条件[19]处理截断边界处的超强反射波。

图1 有限元网格剖分及节点编号示意图

1.2 空间高通滤波

在实现逆时偏移过程中，源点电磁波场和接收点电磁波场的互相关计算不仅会在反射界面处产生强振幅，而且会在电磁波传播整个路径的非反射点处产生强振幅，若将这些振幅沿着时间求和，则会在剖面顶部出现弧形强干扰现象，特别是电性差异的界面会形成呈低波数特征的串扰噪声，这些低频噪声的存在严重影响成像质量。为有效消除这些低频噪声，目前主要采用的去燥方法有：在电磁波场传播过程中消除；应用去噪成像条件，成像后采用滤波法去噪等[20]。其中，采用空间高通滤波法压制低频噪声，具有理论简单、易操作的优点，被广泛应用于GPR逆时偏移成像去燥。为此，本文利用空间高通滤波法[21]对成像结果进行去燥处理，其高通滤波模板计算公式为

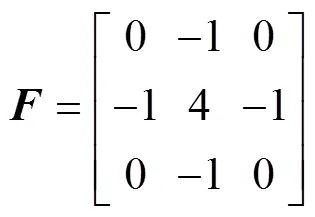
2 归一化互相关成像条件

成像条件的选取是开展高效高精度GPR逆时偏移的关键之一，其选取质量直接影响成像质量。目前，GPR逆时偏移中常用的成像条件主要3种：零时刻成像条件、零延时互相关成像条件和归一化互相关成像条件。

2.1 零时刻成像条件

零时刻成像条件主要应用于等偏移距GPR数据的逆时偏移成像。根据爆炸反射面原理，将等偏移距GPR数据作为边值条件，并以介质半速度进行逆时外推。传播到零时刻的电磁波场就是爆炸反射面的 像[22]，其成像表达式为

其中：(，)为逆时偏移成像剖面；E(，，)为地表接收到GPR数据。采用剖面法进行GPR数据采集时，偏移距一般都较小，难以对高陡地层构造产生的反射波进行有效采集，因此，基于零时刻成像条件的GPR逆时偏移算法难以对复杂结构进行高精度成像。

2.2 归一化互相关成像条件

互相关成像条件最早在弹性波逆时偏移领域被提出，其基本原理[17]是以时间一致性原理为基础，通过计算源点正传电磁波场和接收点反传电磁波场的互相关，从而获得成像剖面。标准的零延迟互相关成像条件公式[7]为

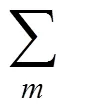
由式(6)和(7)可知：归一化互相关成像条件是在零延时互相关成像条件的基础上，用源点或接收点电磁波场进行归一化，可削弱源强振幅的影响，提升深部反射界面的能量。CHATTOPADHYAY等[23]在弹性波逆时偏移中对上述成像条件进行对比分析，认为源归一化互相关成像条件能够更精确反映地下复杂结构，可提供较准确的成像结果。因此，本文采用源归一化互相关成像条件进行GPR叠前逆时偏移成像。

3 数值算例

3.1 模型一

图2所示为1.80 m×1.25 m(长×宽)的三圆GPR模型示意图，在埋深约0.30 m处存在1条起伏界面。起伏界面上方介质的相对介电常数为5，电导率为0.001 S/m；下方介质的相对介电常数为10，电导率为0.000 5 S/m。起伏界面的下方埋有3个半径为0.05 m的圆形空洞异常体，其圆心位置分别为(0.40, 0.65)，(0.90, 0.90)和(1.40, 1.15) m。利用FETD进行等偏移距和多偏移距测量方式进行正演计算时的发射源信号采用中心频率为500 MHz的雷克子波，采样时间间隔为0.01 ns，时窗长度为35 ns。采用等偏移距测量方式正演时，收、发天线的距离为0.01 m。采用多偏移距测量方式正演时，在地表布设15个发射天线，发射天线的间距为0.10 m，第1个发射天线放置在(0.1,0) m位置处；每个发射天线右侧布置50道接收天线，接收点的间距为0.01 m，水平方向上覆盖长度为0.50 m。

图2 GPR模型一示意图

图3(a)和(b)所示分别为模型一的多偏移距和等偏移距正演剖面。由图3可见：起伏界面和3个圆状异常体的反射波清晰，但这3个圆状异常体产生的反射波不能准确定位异常体的真实空间位置。由此可见，开展GPR逆时偏移成像准确定位异常体的真实空间位置非常必要。

图3 模型一GPR正演剖面

图4(a)和图4(b)所示分别为采用基于归一化互相关成像条件和零时刻成像条件的GPR逆时偏移算法对图3(a)和图3(b)中的数据进行逆时偏移，获得成像剖面。由图4可见：这2种成像条件的逆时偏移获得的剖面中起伏界面形态都非常清晰，绕射波收敛且与真实位置相符。由于模型两端在基于归一化互相关成像条件的叠前逆时偏移成像过程中叠加次数为1，而中间区域进行了多次叠加，因此，界面两端的成像不如中间界面成像清晰。偏移剖面中3个圆状异常体产生的绕射波大部分收敛，并归位到其真实位置。但是对比图3(a)和图4(b)可知：图4(a)中圆状异常体的叠前逆时偏移结果能清晰地反映空洞模型的空间形态和内部结构信息，而图4(b)中基于零时刻成像条件的逆时偏移结果中3个圆状异常体的绕射波能量大都收敛于圆形位置，不能清晰地反映空洞模型的空间分布特征。

为了更好地分析归一化互相关成像条件的优势，分别提取归一化成像条件和零时刻条件的逆时偏移结果在水平位置0.40 m处的单道波形，如图5所示。由图5可知：基于归一化成像条件的逆时偏移结果的单道波形在空洞异常体的顶部和底部都能很好地成像，能大致圈定异常体的垂直分布范围；而基于零时刻成像条件逆时偏移结果的单道波形只能对空洞异常体的底部很好地成像，并且地表产生的直达波非常强烈，压制了后续异常体成像的振幅。对比结果表明：相比于零时刻成像条件的逆时偏移结果，基于互相关成像条件的逆时偏移成像结果分辨率更高，成像质量更好。

(a) 归一化互相关成像条件；(b) 零时刻成像条件

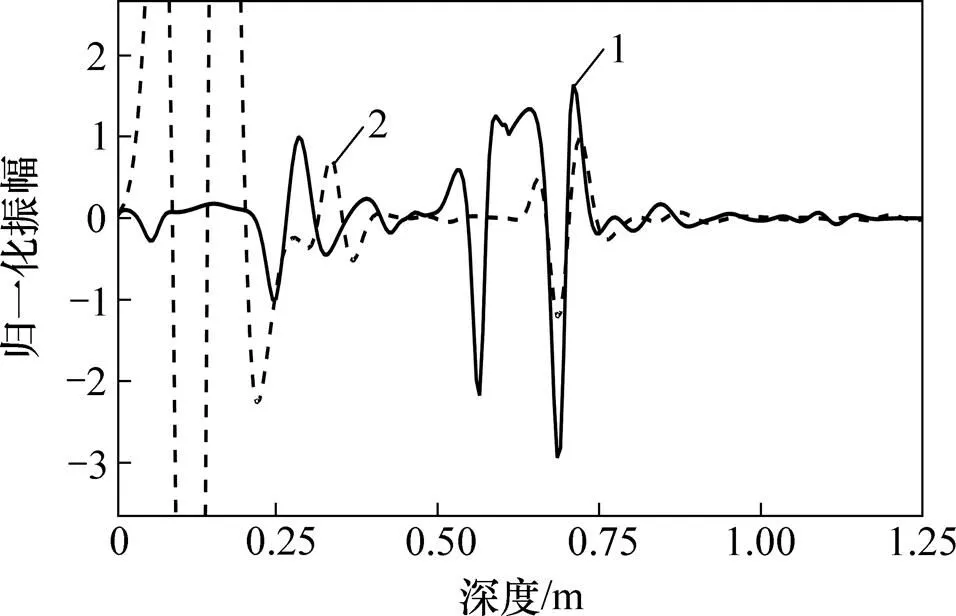
1—归一化互相关成像条件；2—零时刻成像条件。

Fig. 5 Comparison of single waveform of RTM profiles of model 1 at horizontal position of 0.40 m

3.2 模型二

模型二为1.80 m×1.25 m(长×宽)的矩形区域，埋深约0.30 m处存在1条起伏界面，如图6所示。起伏界面上方和下方介质的相对介电常数和电导率与模型一的相同。起伏界面下方分别埋有1个半径为0.05 m的圆状空洞异常体和1个边长为0.10 m的正方形空洞异常体，圆状空洞异常体的圆心位置为(0.40, 0.65) m，正方形空洞异常体的中心位置为(1.40, 0.65) m。利用FETD进行等偏移距和多偏移距测量方式进行正演计算时的发射源信号采用中心频率为500 MHz的雷克子波，采样时间间隔为0.01 ns，时窗长度为35 ns。采用等偏移距测量方式正演时，收发天线的距离为 0.01 m。采用多偏移距测量方式正演时，在地表布设15个发射天线，发射天线的间距为0.10 m，第1个发射天线放置在(0.10,0) m位置；每个发射天线右侧布置50道接收天线，接收点的间距为0.01 m，水平方向上覆盖长度为0.50 m。

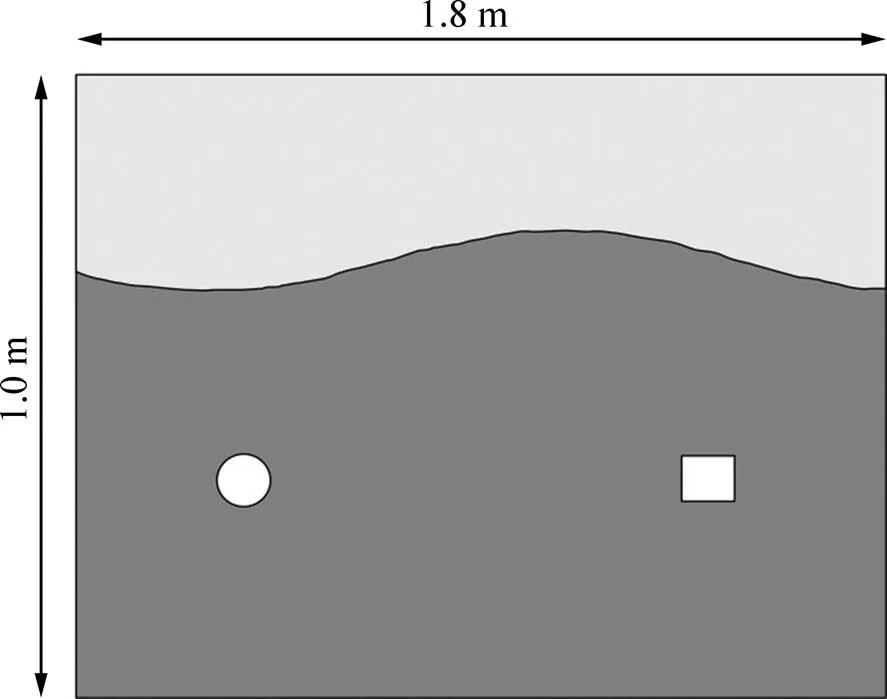
图6 GPR模型二示意图

图7(a)和图7(b)所示分别为模型二的多偏移距和等偏移距正演剖面。由图7可见：起伏界面、圆状异常体和正方形空洞异常体的反射波清晰可见，但是圆状异常体和正方形空洞产生的反射波不能准确定位其真实空间位置。为此，对图7中的多偏移距和等偏移距数据分别利用基于归一化互相关成像条件和基于零时刻成像条件的GPR逆时偏移算法进行逆时偏移成像。图8(a)和图8(b)所示为分别利用图7(a)和图7(b)中的数据进行GPR逆时偏移成像的结果。

由图8可见：偏移剖面中3个圆状异常体产生的绕射波大部分收敛，并归位到其真实位置。但对比图8(a)和图8(b)可知：图8(a)中圆状异常体的叠前逆时偏移结果能清晰地反映空洞模型的空间形态和内部结构信息，而图8(b)中叠后逆时偏移结果中3个圆状异常体的绕射波能量大都收敛于圆形位置，不能清晰地反映空洞模型的空间分布特征。图9所示为2种成像条件的逆时偏移结果在水平位置0.40 m处的单道波形。由图9可知：基于归一化成像条件的逆时偏移结果的单道波形在空洞异常体的顶部和底部都能很好地成像，能大致圈定异常体的垂直分布范围；而基于零时刻成像条件逆时偏移结果的单道波形只能对空洞异常体的底部很好地成像，并且地表产生的直达波非常强烈，压制了后续异常体成像的振幅。对比结果表明：相比于零时刻成像条件的逆时偏移结果，基于互相关成像条件的逆时偏移成像结果的分辨率更高，成像质量更好。

(a) 多偏移距GPR正演剖面；(b) 等偏移距GPR正演剖面

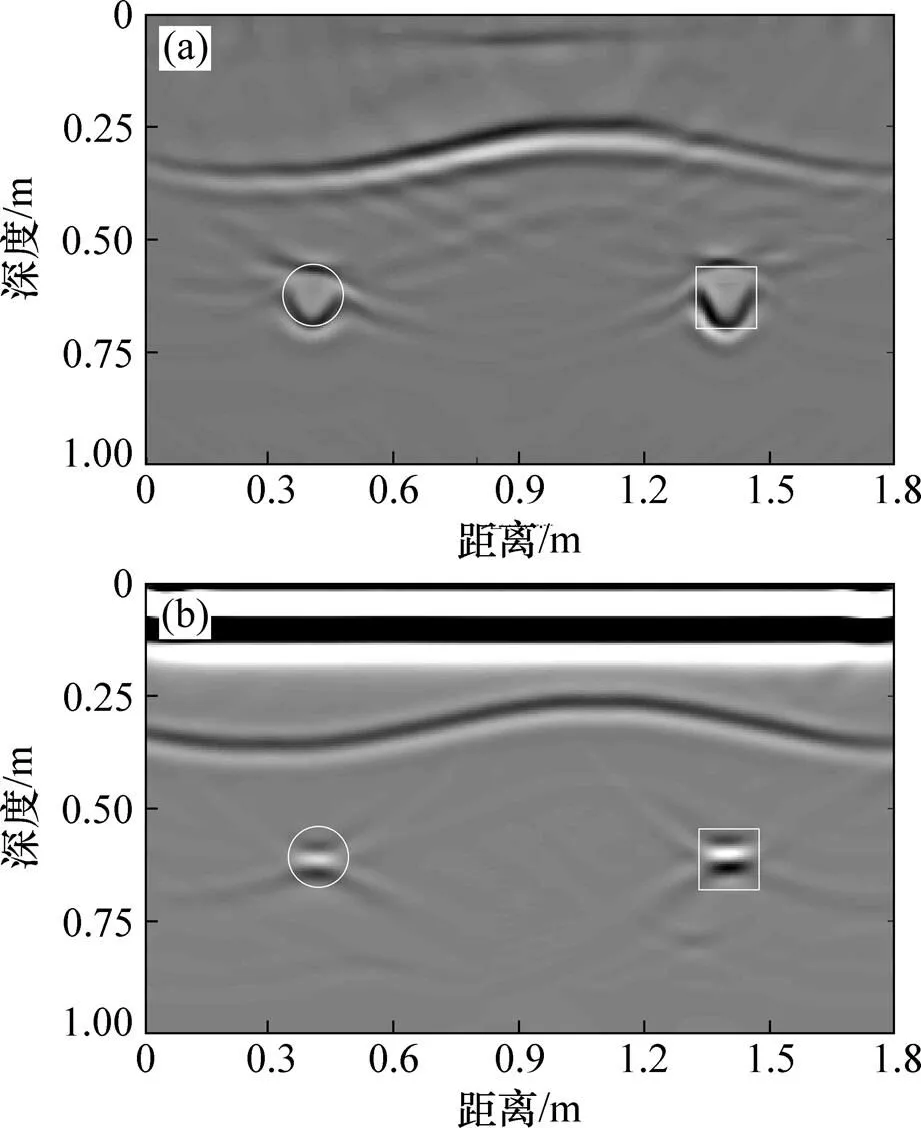
(a) 归一化互相关成像条件；(b) 零时刻成像条件

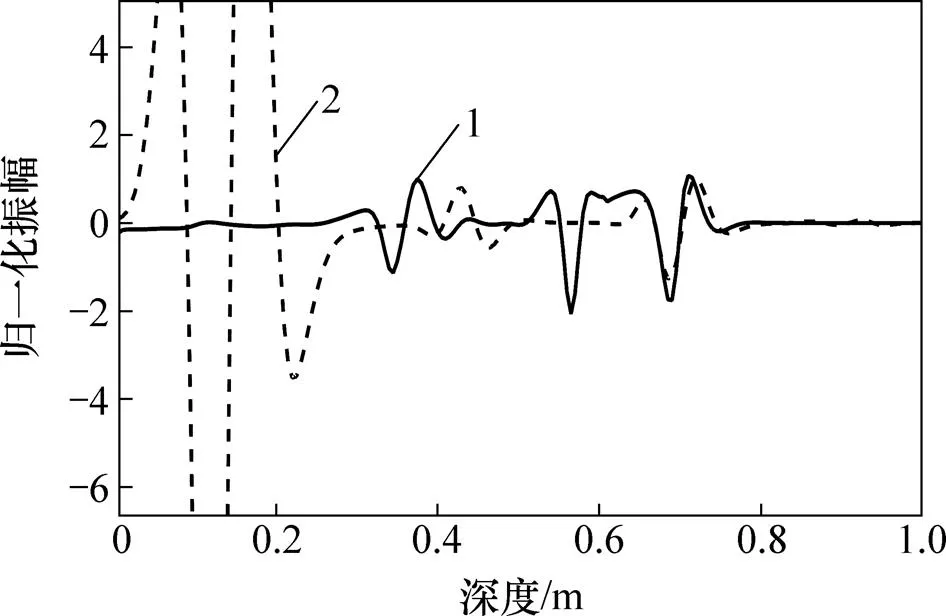
1—归一化互相关成像条件；2—零时刻成像条件。

4 结论

1) 为提高GPR数据的逆时偏移计算精度，将归一化互相关成像条件引入到GPR的逆时偏移成像中。

2) 采用基于三角形剖分的FETD模拟电磁波场的正向及逆向传播，可获得基于归一化互相关成像条件的GPR逆时偏移成像剖面。

3) 基于归一互相关成像条件的GPR逆时偏移方法能更精细地刻画出模型中异常体的空间形态和内部结构特征，提高了GPR对异常体的探测分辨率。

[1] 刘澜波, 钱荣毅. 探地雷达: 浅表地球物理科学技术中的重要工具[J]. 地球物理学报, 2015, 58(8): 2606−2617.LIU Lanbo, QIAN Rongyi. Ground penetrating radar: a critical tool in near-surface geophysics[J]. Chinese Journal of Geophysics, 2015, 58(8): 2606−2617.

[2] ALANI A M, ABOUTALEBI M, KILIC G. Applications of ground penetrating radar(GPR) in bridge deck monitoring and assessment[J]. Journal of Applied Geophysics, 2013, 97(13): 45−54.

[3] CHANG C W, LIN C H, LIEN H S. Measurement radius of reinforcing steel bar in concrete using digital image GPR[J]. Construction and Building Materials, 2009, 23(2): 1057−1063.

[4] SOLLA M, LORENZO H, RIAL F I, et al. GPR evaluation of the Roman masonry arch bridge of Lugo (Spain)[J]. Nondestructive Testing and Evaluation International, 2011, 44(1): 8−12.

[5] 戴前伟, 冯德山, 何继善. Kirchhoff偏移法在探地雷达正演图像处理中的应用[J].地球物理学进展, 2005, 20(3): 849−853. DAI Qianwei, FENG Deshan, HE Jishan. The application of Kirchhoff's migration method in the image processing of the ground penetrating radar forward simulation[J]. Progress in Geophysics, 2005, 20(3): 849−853.

[6] BITRI A, GRANDJEAN G. Frequency-wavenumber modelling and migration of 2D GPR data in moderately heterogeneous dispersive media[J]. Geophysical Prospecting, 1998, 46(3): 287−301.

[7] 雷林林, 刘四新, 傅磊, 等.基于全波形反演的探地雷达数据逆时偏移成像[J]. 地球物理学报, 2015, 58(9): 3346−3355. LEI Linlin, LIU Sixin, FU Lei, et al. Reverse time migration applied to GPR data based on full wave inversion[J]. Chinese Journal of Geophysics, 2015, 58(9): 3346−3355.

[8] 朱尉强, 黄清华.探地雷达衰减补偿逆时偏移成像方法[J]. 地球物理学报, 2016, 59(10): 3909−3916. ZHU Weiqiang, HUANG Qinghua. Attenuation compensated reverse time migration method of ground penetrating radar signals[J]. Chinese Journal of Geophysics, 2016, 59(10): 3909−3916.

[9] FISHER E, MCMECHAN G A, ANNAN A P, et al. Examples of reverse-time migration of single-channel, ground-penetrating radar profiles[J]. Geophysics, 1992, 57(4): 577−586.

[10] LEUSCHEN C, PLUMB R. A matched-filter approach to wave migration[J]. Journal of Applied Geophysics, 2000, 43(2): 271−280.

[11] ZHOU H, SATO M, LIU H. Migration velocity analysis and prestack migration of common-transmitter GPR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(1): 86−91.

[12] 冯德山, 戴前伟.基于小波多分辨探地雷达三维正演模拟及偏移处理[J]. 中南大学学报(自然科学版), 2007, 38(4): 758−763. FENG Deshan, DAI Qianwei. GPR three dimension forward simulation and migration processing with multi-resolution of wavelets[J]. Journal of Central South University(Science and Technology), 2007, 38(4): 758−763.

[13] BRADFORD J H. Reverse-time prestack depth migration of GPR data from topography for amplitude reconstruction in complex environments[J]. Journal of Earth Science, 2015, 26(6): 791−798.

[14] 戴前伟, 张彬, 冯德山, 等. 探地雷达各向异性介质有限差分偏移线性变换[J]. 中南大学学报(自然科学版), 2012, 43(5): 1814−1820. DAI Qianwei, ZHANG Bin, FENG Deshan, et al. Linear transformation of finite difference migration of GPR in anisotropic medium[J]. Journal of Central South University(Science and Technology), 2012, 43(5): 1814−1820.

[15] 傅磊, 刘四新, 刘澜波, 等.机载探地雷达数值模拟及逆时偏移成像[J]. 地球物理学报, 2014, 57(5): 1636−1646. FU Lei, LIU Sixin, LIU Lanbo, et al. Airborne ground penetrating radar numerical simulation and reverse time migration[J]. Chinese Journal Geophysics, 2014, 57(5): 1636−1646.

[16] LIU Sixin, LEI Linlin, FU Lei, et al. Application of pre-stack reverse time migration based on FWI velocity estimation to ground penetrating radar data[J]. Journal of Applied Geophysics, 2014, 107(4): 1−7.

[17] CLAERBOUT J F, JOHNSON A G. Extrapolation of time-dependent waveforms along their Path of Propagation[J]. Geophysical Journal International, 1971, 26(1/2/3/4): 285−293.

[18] 戴前伟, 王洪华, 冯德山, 等.基于双二次插值的探地雷达有限元数值模拟[J]. 地球物理学进展, 2012, 27(2): 736−743. DAI Qianwei, WANG Honghua, FENG Deshan, et al. Finite element numerical simulation for GPR based on quadratic interpolation[J]. Progress in Geophysics, 2012, 27(2): 736−743.

[19] DROSSAERT F H, GIANNOPOULOS A. A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves[J]. Geophysics, 2007, 72(2): T9−T17.

[20] 刘红伟, 刘洪, 邹振, 等.地震叠前逆时偏移中的去噪与存储[J]. 地球物理学报, 2010, 53(9): 2171−2180. LIU Hongwei, LIU Hong, ZHOU Zhen, et al. The problems of denoise and storage in seismic reverse time migration[J]. Chinese Journal Geophysics, 2010, 53(9): 2171−2180.

[21] 张智, 刘有山, 徐涛, 等. 弹性波逆时偏移中的稳定激发振幅成像条件[J]. 地球物理学报, 2013, 56(10): 3523−3533. ZHANG Zhi, LIU Youshan, XU Tao, et al. A stable excitation amplitude imaging condition for reverse time migration in elastic wave equation[J]. Chinese Journal Geophysics, 2013, 56(10): 3523−3533.

[22] SCHLEICHER J, COSTA J, NOVAIS A. A comparison of imaging conditions for wave-equation shot-profile migration[J]. Geophysics, 2008, 73(6): S219−S227.

[23] CHATTOPADHYAY S, MCMECHAN G A. Imaging conditions for prestack reverse-time migration[J]. Geophysics, 2008, 73(3): S81−S89.

(编辑 陈灿华)

Reverse time migration of ground penetrating radar based onnormalized cross correlation imaging condition

CHEN Depeng1, 2, 3, DAI Qianwei1, 2, FENG Deshan1, 2, WANG Honghua3, ZHANG Bin1, 2

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring,Ministry of Education, Changsha 410083, China;3. School of Earth Sciences, Guilin University of Technology, Guilin 541004, China)

On account of the low imaging precision of ground penetrating radar (GPR) reverse time migration (RTM) based on the zero time imaging condition and it is difficult to imaging complex structure with high resolution, normalized cross-correlation imaging conditions was applied in GPR pre-stack RTM imaging. Based on the two-dimensional GPR wave equation, the time domain finite element method based on perfectly matched layer (PML) boundary condition (FETD) was used to simulate the forward and reverse electromagnetic waves, normalized cross-correlation imaging condition was used to obtain the pre-stack RTM results, the spatial high-pass filtering was applied to suppress cross-correlation process of low frequency noise and the corresponding program of GPR pre-stack RTM based on normalized cross-correlation imaging condition was designed and implemented. After that, the two complex GPR models were established and calculated by GPR RTM program based on the normalized cross-correlation imaging condition and zero time imaging condition, respectively. The results show that, compared with imaging results with zero time imaging condition, the imaging results with those in the normalized cross-correlation imaging condition have higher image quality and can more clearly display the detailed spatial form and internal structure information of the abnormal body space.

ground penetrating radar; reverse time migration; normalized cross correlation imaging condition; zero time imaging condition

10.11817/j.issn.1672−7207.2018.05.025

P631

A

1672−7207(2018)05−1221−07

2017−10−10；

2017−12−08

国家自然科学基金资助项目(41374118, 41574116, 41604102, 41704128)；广西自然科学基金资助项目(2016GXNSFBA380082, 2016GXNSFBA380215)(Projects(41374118, 41574116, 41604102, 41704128) supported by the National Natural Science Foundation of China; Projects(2016GXNSFBA380082, 2016GXNSFBA380215) supported by Guangxi Natural Science Foundation)

戴前伟，博士，教授，从事电磁方法及理论研究；E-mail: qwdai@csu.edu.cn