以《5的乘法口诀》为例谈数学经验的积累

文碧平

【摘要】本文以《5的乘法口诀》教学为例，引导学生通过操作活动领悟乘法的本质意义，通过语言表征积累感性经验，通过观察思考积累数学经验，通过应用拓展积累解题经验。

【关键词】《5的乘法口诀》 数学经验 积累

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2018）02A-0110-02

语言表征，是语言材料所承载的信息在神经中枢内的存储形式。人教版二年级上册《5的乘法口诀》是学生学习乘法口诀的入门课。在长期的教学实践中，笔者发现，在学习这部分内容之前，很多学生已经掌握了基本的乘法意义，生活中也不乏以数字“5”为基本单位的计数习惯。如果照本宣科，显然辜负了教材编者的深意。基于此，在教学《5的乘法口诀》时，笔者引导学生进行了多轮操作活动，让学生领悟乘法的本义，并逐渐让学生通过语言表征的复制累积来积累感性经验，为编制新口诀打牢基础。

一、在活动中积累语言表征

探究活动1：拼接1个图形需5根火柴棒，拼接2个同样的图形，共需几根火柴棒？要求学生边拼接边说明意图，然后列式计算。有的学生列式为：5+5=10，有的学生列式为5×2=10或2×5=10。教师板书：拼装一个图形用火柴棒（ ）根，有（ ）个构图，共用（ ）根？为学生的语言表征提供理性材料。

探究活动2：每幅构图用5根，组接3幅构图。要求学生先审题解说，再提问列式。学生列式为：5+5+5=15，5×3=15或3×5=15。

探究活动3：每幅构图用5根，组接4幅构图。要求学生心算出小棒数，并追问“为什么”，让学生领悟4个5合并是20，并且领会“4×5=20”或“5×4=20”的意义。

探究活动4：每幅构图用5根，组接5幅构图，共需多少根小棒？学生列式为：5+5+5+5+5=25，5×5=25。辩论：算式中两个因数“5”的含义一样吗？这一过程不仅强化学生对题干中“每幅5根、5幅构图、小棒总量”各数量的理解，同时深化对乘法意义的认识。在循序渐进的操作活动中，让学生感知“每图5根×构图数量=总根数”这一数量关系，复制累积乘法意义的语言表征。同时，也让学生在操作活動中真切感知1个5、1个5逐渐加码增值的过程，为探究乘法口诀奠定基础。另外通过“为什么还要回溯到加法”的辩论，让学生意识到“乘法”是若干个加数相同的加法的简算形式。

二、在观察中积累感性经验

现实情境既是学生列式的根据，又是选择算法的依据，学生解题时应该清楚地了解情境特性，才能读懂题意，正确解答。为此，在观察情境图、提取数学信息与发现数学问题的基础上，笔者引导学生通过画点阵图来解构题意，感受各个数据的特点，为后续探索乘法口诀积累感性经验。笔者分三步引导学生观察。

步骤1：观察情境图1，解析题意，列式计算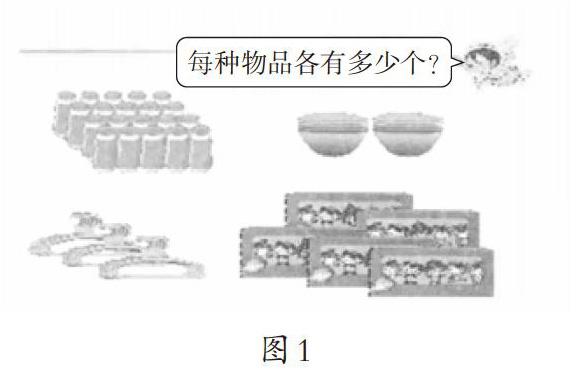

学生解读：每排蒙牛酸奶有5瓶，有4排，共有几瓶蒙牛酸奶？每摞碗有5只，有2摞，共有几只碗？每打衣架有5枚，有3打，共有几枚衣架？每个礼盒有5个福娃，有5个礼盒，共有几个福娃？

在观察与分析的过程中，学生更加深入地理解了乘法的意义。同时，“每份数×份数=总数”的数量关系更加入脑入心。

步骤2：引进点阵图，画一画

在学生进行上述探究后，接着讨论。

师：如果简化上述情景，删繁就简，提取精华，还可以画出更精炼的简图吗？

师：可以用多彩小圆点表示。

学生画出并观察每幅点阵图（如下图2、图3、图4、图5所示）。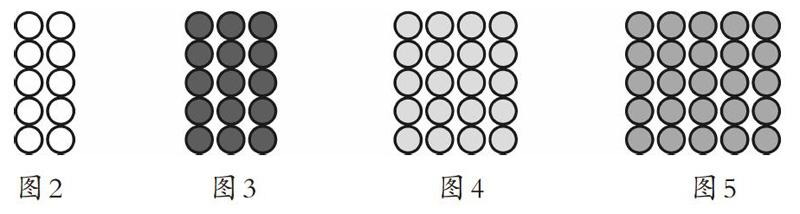

步骤3：逐渐抽象，推出乘法口诀

在点阵图的基础上，教师引导学生将表征形式载体从现实情境转化为图形、符号和语言，积累抽象经验。

探讨图2的点阵图时，教师引出：2×5=10或5×2=10，2个5合并是10，随后及时点拨：2个5合并是10，比用图和算式表示更简洁的还有“乘法口诀”，即“二五一十”。在你们的印象中，口诀“二五一十”短短四个字中含有哪些信息？

生1：“二五”就是2个5，分别标识两个乘数。

生2：“一十”标识积为10。

生3：书写时用大写数字。

生4：乘法口诀简单易记，为以后的复杂乘法计算服务。

在学生明晰了“乘法口诀”内涵后，教师要求学生带着经验和原理编出余下的几句口诀。在独立编创、相互交流、指正修改、展示汇报后，教师出示“5的乘法口诀”（一五得五、二五一十、三五十五、四五二十、五五二十五、五六三十、五七三十五、五八四十、五九四十五）。

三、在应用中积累解题经验

引导学生在运用“5的乘法口诀”解决实际问题时，除了围绕“每份数、份数与总数”等数量关系解答，笔者还进行了适当的拓展（如图6所示）。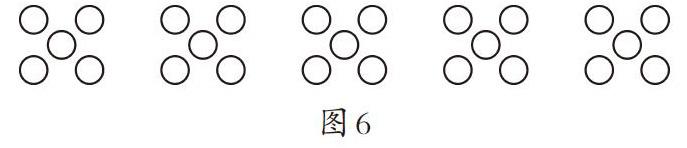

教师问：每组5个圆圈，有5组图形，一共有多少个圆圈？生答：5×5=25（个），口诀是“五五二十五”。教师追问：“你是怎么想到这句口诀的？”学生感知到“乘法中的两个因数均可作为口诀的线索”，提高了运用乘法口诀的灵活度和效率。

同理，如图7，每纵列5个，有4列，一共有几个？5×4=20（正）或4×5=20（副）；将前图进行翻转，呈现图8，改列为行，有4行，每行5个，一共有几个？4×5=20（正）或5×4=20（副）。

这样拓展“5的乘法口诀”的意图是：一方面用点阵图将数量关系从复杂的情境图中解放出来，简化为数学模型；另一方面引导学生转换视角观察图形，体会观察的角度不同，乘法口诀中两个因数的含义可以置换。这样教学，不但让学生积累了观察经验，而且得知每份数与份数的相对关系，自然而然地将“几个几”与“行与列”对应起来。

教学至此，教师还可以先单独呈现图6、图7、图8并单独探讨，然后一起呈现3幅图，要求学生提问列式并求解。随着“一共有几个点子”的问题提出，出现了25+20+20=65转化为25+20×2=65，潜移默化地引导学生运用乘法解决问题；还涌现了20×3+5=65这样的创意算式，这是对“25+20+20=65”的变通处理，说明学生对乘法意义的运用已经很精通熟练了。当然，“13×5”的出现，是基于对“每个单元图5个点子，共有13幅单元图，总共有13×5个点子数”这一数量关系的深刻解读后得到的，即“每份数×份数=总数”的再运用。

如此拓展，不仅重申了加法与乘法的亲缘关系，深究了乘法意义的本质，而且让学生感受到观察、思考、转换等对于解决问题能起到积极的作用，不断积累实用经验。

（责编 林 剑）