社会资本退出PPP项目财务可行性及退出时间选择研究

孙 慧， 刘 思， 王宇宁

(1． 天津大学管理与经济学部， 天津 300072； 2． 天津师范大学城市与环境科学学院， 天津 300387)

2014年财政部发布《关于推广运用政府和社会资本合作模式有关问题的通知》以及发改委同期发布的《国家发展改革委关于开展政府和社会资本合作的指导意见》以来，PPP项目在全国各地积极推进。据统计，截止到2016年6月末，全部入库项目9 285个，落地率23.8%。其中已录入信息的53个示范性项目，落地周期在6个月到43个月之间，平均13.5个月。落地难、落地周期长，很大程度因为社会资本参与PPP项目的积极性不够。一方面，PPP项目寿命期长，资本回收期长，社会资本参与PPP项目的目的并不相同，其退出缺乏成熟途径；另一方面，纵使社会资本有意向参与PPP项目全程，也受企业的平均寿命和专业擅长领域限制，难以在全寿命周期发挥优势。另外，Demirag[1]对PPP融资人进行调查的结果显示，有20%左右的融资人表示会提前退出。因此，深入研究社会资本退出PPP项目的可行性、退出时机的选择，促进联合体在PPP项目中发挥各自优势很有必要。

一、 研究现状

PPP项目模式引起了我国学术界的广泛关注，在法律和经济领域均有学者对PPP的推行和合作等问题进行探讨，然而对PPP发起后社会资本的退出需求的研究较为缺乏。一是因为目前我国PPP项目极少有进入移交阶段，大量合作崩盘的矛盾还未出现；二是因为PPP模式正在不断尝试和摸索阶段，政府与社会资本更倾向于从一而终的中规中矩合作方式。国外已经有学者关注到PPP项目资金交易的二级市场问题，并提出现金流折现模型是研究PPP二级市场问题的有力工具[2]。Albomoz运用现金流折现模型讨论了发达国家和发展中国家是否存在PPP二级市场，即社会资本中途退出PPP项目的可能性[3]。

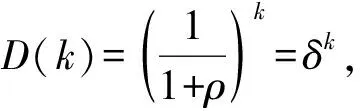
为了改进DCF方法的不足，Loewenstein和Prelec提出了双曲线折现函数，用来描述人们不耐心程度递减的状况，其特点是短期的折现率比长期折现率更高，即折现率会随着时间推移而逐渐减小[11]。虽然双曲折现能否准确地反映决策者的折现行为仍然是一个值得考虑的问题，但是相对于指数折现来说，双曲折现更符合个体行为，更能解释决策者行为异常现象。正如Prelec指出，几乎没有哪个理论如双曲折现那样被广泛接受[12]。

针对中国国情和模型的实操性，对西班牙学者Albornoz的模型进行了3点改进。第一点，本文模型考虑了退出时间这一变量对退出可行性的影响，并探讨了退出时间的选择，而不是仅讨论在建设期结束退出PPP项目，且总寿命期恰巧能被建设期整除这一种情况，更具有实际操作性。第二点，本文从社会资本角度出发，考虑决策者时间偏好不一致这客观事实，采用了经济行为学中折现率递减的假设，更贴近社会资本的现实想法。第三点，在模型应用方面，文章充分考虑我国实际情况，对关键变量进行合理取值，得出的结论更适用于我国。

二、 PPP项目二级市场存在的合理性分析

1. 充分发挥社会资本竞争力

PPP项目周期长，长时间占用合作者资源的特点，在某种程度上降低了社会资本参与的热情和积极性。而二级市场的存在，可以让各类社会资本自主选择参与时间，在擅长的项目阶段发挥优势，在短板领域被其他竞争者取代，优劣互补，提高PPP项目的效率和质量，也符合我国市场化推进的方向。

2. 丰富的接盘资金

二级市场的存在鼓励那些厌恶风险，但有实力的资金进入PPP项目，丰富了社会资本种类。对养老基金这类寻求低风险、长期稳定回报率的机构具有吸引力，并且这些公司的专业性和对特定风险的管控能力更强，也更适合在项目中后期发挥作用。

3. 退出渠道多样化

理论上，社会资本的退出方式有股权转让、公开上市、发行债券、资产证券化和清算等。2015年出台的《项目收益债试点管理办法》降低了项目收益债的发行门槛，对PPP项目社会资本的退出起到支持性作用。2017年3月我国首批四单PPP资产证券化产品成功发行，也标志着我国PPP二级市场已有雏形。

三、 社会资本退出PPP项目的财务可行性分析模型构建

1. 设立决策方案

假设某社会资本A公司准备参与某PPP项目，在做投资决策时，A公司有两种方案可以选择(仅投资策略不同)。

方案I：以I作为股权资金投入到寿命期为n的PPP项目，并运营至整个寿命期结束。

方案II：以I作为股权资金投入相同的PPP项目，建设期结束后，在运营期第f年退出项目，通过PPP二级市场以价格V转卖给接盘的社会资本。A公司退出该PPP项目后资金不会闲置，将会重复上一周期的行为，以I投资于相似的PPP项目，至运营期第f年，通过PPP二级市场再次卖掉股权，如此循环至第n年。

2. 基本假设

本文从财务角度分析社会资本退出的可行性，因此选取现金流净现金值作为评价标准。方案II的财务指标优于方案I，则退出PPP项目更有利，即PPP二级市场具有存在的可能性。另外，当采用双曲折现率进行财务评价时，计划最优和实际最优不匹配，即最优决策存在时间不一致性，因此，处于不同时期的同一决策者应视为不同的决策者。本文社会资本A公司的决策点始终设为t=0，因此其双曲折现率函数唯一。同时，二级市场的接盘公司在整个循环决策中，是不同决策者不同决策时间点，我们将其简化为相似公司，且均为成熟型决策者，这样可以做到决策时间上一致。基于以上分析，本文做出4条基本假设。

(1) 假设1：A公司在两种方案下现金流情况相同，且二级市场中的接盘公司与A公司现金流一致。一方面，在政府、项目其他利益相关者的有效监督下，A公司在项目建设期压低成本以提高利润，影响项目交付质量的投机行为将不会发生；另一方面，这种投机行为会导致A公司在退出PPP项目时，二级市场的卖出价值降低，所以某种程度上A公司的收益总和是不变的；另外，二级市场中的接盘公司与A公司资质和能力相同，提供服务和获利的能力相同。为简化模型，假设现金流量平均，每年相等。

(2) 假设2：方案I的折现率低于方案II。在方案II中，A公司在PPP项目中期退出并投资新的PPP项目，这种循环需要多次地进入和退出项目，增加了交易成本，同时加大了投资者风险，风险明显大于方案I。根据风险与收益对等原则，假设2成立。

(3) 假设3：接盘公司的折现率低于A公司。PPP项目风险随时间递减[13]，项目建设期风险最大，且随着运营期的推进，项目信息逐渐完善，不确定性降低，风险逐渐变小。因此，二级市场中的接盘公司在建设期后进入PPP项目，也是一种规避风险的选择。同样根据风险与收益对等原则，假设3成立。

(4) 假设4：决策时点是第一年年初，若A公司方案II的现金流净现值比方案I大，则说明存在PPP二级市场空间。

3. 模型构建

在方案I中，社会资本A公司不在期中退出PPP项目，运营至项目寿命期结束，该项目现金流量见图1。评价模型关键参数的含义见表1。方案I净现金流公式为

(1)

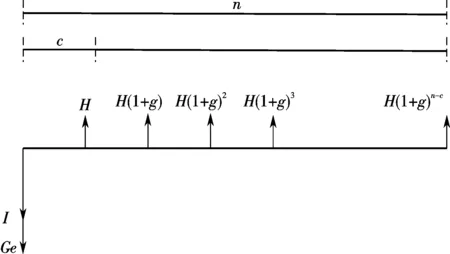
图1 方案I 现金流量

在方案II中，社会资本A公司有计划地在运营期第f年时退出该PPP项目，并投资相似的新PPP项目，如此循环m次。值得注意的是，最后一次循环在运营期第f年退出后，不再投资新项目，否则剩余年限收不回投资成本。该项目现金流量见图2。方案II净现金流公式为

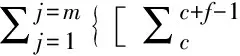
(2)

(3)

Vj=V1(1+g)(j-1)(c+f)

(4)

图2 方案II 现金流量

在式(2)中，前两项是项目建设期投资额和进入的交易成本；第3项是m个循环中社会资本退出PPP项目时转卖获得的卖价；第4项是m-1个循环中投入新项目的建设期成本；第5项是m个循环中的运营期收入。令NPV1=0，即方案I刚好财务可行，NPV2-NPV1=s，则有

(5)

则有当s>0时，方案II优于方案I，评价结果为社会资本中途退出PPP项目在财务上可行，二级市场中存在社会资本接盘的空间。由s表达式可知，两方案的差值与运营期现金流H、退出项目的交易成本Gs、各个折现率r1、r2、y，通货膨胀系数g及各时间值有关。结合我国实际情况，对各关键变量的取值范围进行界定。

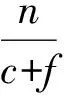
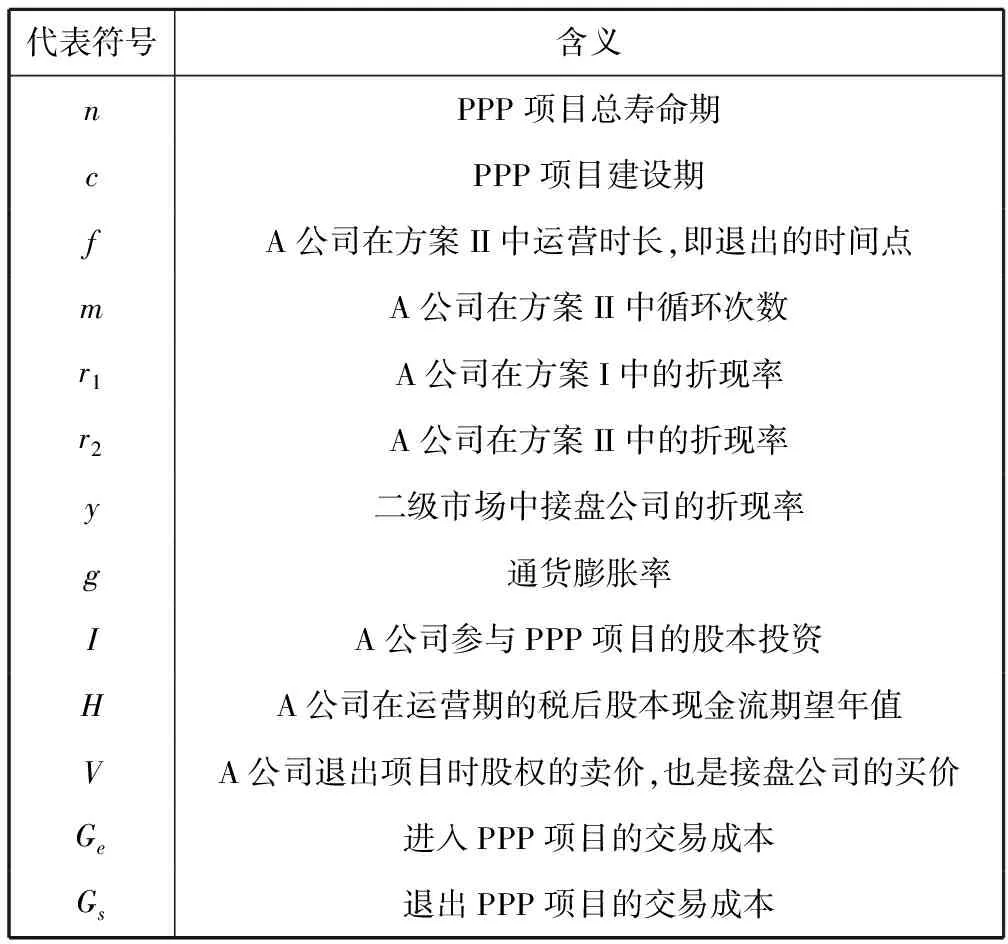
表1 财务可行性评价参数表

(2) 折现率。国家发改委颁布的《建设项目经济评价方法与参数》中指出：现阶段我国社会折现率取值为8%，对于周期超长的项目，如果远期效益较大，项目实现收益的风险较低，社会折现率可随时间延长适当递减，但不应低于6%，其中并未给出递减取值具体做法。中交公路规划设计院有限公司在《桥梁工程全寿命设计理论与方法研究报告》给出的长周期实际折现率的取值范围为1.9%～2.97%，以30年为一阶段进行分段取值。Weitzman的高权威问卷调查显示，折现率离散系数为σ/μ=3/4不变，呈Gamma分布，均值是4%，标准差是3%，折现率随时间递减[15]。邵颖红等采纳Weitzman的问卷调查结果，结合我国当前的社会折现率水平，计算出递减社会折现率的取值，1～10年取6%～8%，11～17年取5%，18～28年取4%，29～50年取3%，51～100年取2%，计算期超过100年取1%[16]。最被广泛接受的两个递减折现率函数，一个是Loewenstein和Prelec提出的连续型双曲线折现函数式(6)，另一个是改进后的离散型准双曲线折现函数式(7)，即

d(t)=(1+αt)-γ/α

(6)

(7)

式中：系数δ为标准折现率，表示一致的时间偏好；β为非一致的时间偏好[6]。本文结合权威学者的研究及我国基础类设施项目的折现率现状，采用两种折现率分别进行评价：固定折现率取8%～10%；递减折现率采用Weitzman的高权威问卷调查结果，在Crystal Ball软件中随机生成1 000个离散系数为0.75，服从Gamma分布的随机数，由随机数的平均值得到0～n年等效折现率，然后拟合出莱布森离散型折现函数表达式，对β进行赋值。r1为A公司在方案I中的折现率；r2为A公司在方案II中的折现率；y为二级市场中接盘公司的折现率。三者均值关系为r2>r1>y。这里的折现率是指名义折现率，与现金流预测值相对应。

(3) 现金流。PPP项目中的股本资金现金流一般在项目建设期为负，在运营期为正[4]。因此，评价模型可简化为建设期股本投资为I，运营期年金为H的现金流形式，其中I>0，H>0。A公司进入和退出PPP项目时，会产生交易成本，分别用Ge、Gs表示。关于PPP交易成本的研究很少，且大部分从政府角度出发，关注准入交易成本。PPP项目的准入交易成本主要取决于招投标形式。Schez和Gago对欧洲投资银行的研究显示，当项目以协商形式投标时，绿地PPP交通项目中标者的交易成本为2.85%，总体上看，所有参与者的平均交易成本为10%[17]。Esty估计项目的融资成本为5%～10%[18]。项目退出时的交易成本鲜有研究，可用股本投资额I的百分率表示。V是方案II中A公司退出PPP项目时获得的卖价，也是二级市场中接盘公司接盘项目的买价，在这里等于从A公司在c+f年退出时，至该项目寿命期结束时，接盘公司获得的现金流净现值。A公司在第一次循环中退出PPP时获得V1，第二次循环中获得V2，以此类推，最后一次获得Vm。运营期收益年金为H的现金流预测值为H，H(1+g)，H(1+g)2，H(1+g)3，…,H(1+g)n。式中，g表示通货膨胀因素，取我国近十年(2007～2016年)居民消费价格指数CPI均值，即g取2.93%。

最后，对参数进行赋值，用MATLAB模拟出s与关键指标H、Gs、r1、r2、y、g、c、f、n关系曲线，讨论社会资本退出PPP的可行域。

四、 模型应用

在模型应用的过程中，对比分析折现效用函数分别为指数型折现和准双曲线型折现时，各关键指标对社会资本退出PPP的可行域的影响。

1. 指数型折现时PPP项目退出的可行性分析

将参数赋初始值，其中进入PPP项目的交易成本和退出的交易成本由股本投资I的百分数表示，见表2。

表2 参数初始值

用MATLAB运行得到两种方案现金流净现值之差s与退出时间f的函数关系，见图3。f代表循环中每次退出前的运营时间，观察函数走势可知，s基本随f的增大而递减。递减速率逐渐变小，这是因为随着退出时间的推迟，循环次数m递减的速率变慢，而且循环次数m越小，资金利用效率越低。第13～14年函数图形存在短阶段波动，这是因为当f≥14时，循环次数，在方案II劣势的情况下，社会资本退出PPP项目后不再投资于新PPP项目，是优选的。f≥6后，s<0，说明社会资本退出PPP项目的时间可行域有限，且在建设期后尽早退出，在财务上更可行。

图3 两方案现金流净现值之差与社会资本退出时间的函数关系

下面分析社会资本折现率、接盘公司折现率和社会资本退出PPP项目的交易成本这几个关键指标对两方案现金流净现值之差s及退出时间f可行域的影响(见图4)

由图4显示的模拟结果可以得到如下结论。

r2是社会资本在方案II中的折现率，其值表示社会资本有计划地退出PPP项目时社会资本的资金报酬率期望值，在初始值10%的基础上，上下均匀取值。s随r2值单调递减，且函数曲线互相不存在交点，与x轴交点逐渐向左移动，f可行域在缩小。

r1是社会资本在方案I中的折现率，其值表示社会资本计划运营至PPP项目结束的资金报收率期望值，在初始值9%的基础上，上下均匀取值。s随r1值单调递增，且函数曲线互相不存在交点，与x轴交点逐渐向右移动，f可行域在增大。当r1降到一定程度时，社会资本不存在退出可行区域。

y是接盘公司的折现率，其值表示二级市场中有意愿在中途参与到PPP项目的社会资本的资金报酬率期望值，在初始值8%的基础上，上下均匀取值。s随y值单调递减，且函数曲线互相不存在交点，当y值大于r1后，社会资本几乎不存在退出可行区域。

Gs是社会资本退出PPP项目的交易成本，用初始投资I的百分比表示，在初始值0%的基础上，上下均匀取值。s随Gs值单调递减，且函数曲线互相不存在交点，当f≥14后，Gs的取值对于评价结果无影响，当Gs值大于15%后，社会资本几乎不存在退出可行区域。

图4 关键指标变动对f-s 函数的影响

2. 准双曲线型折现效用函数

通过下面4个步骤拟合出准双曲线型折现效用函数。

(1) 以r2=10%为当前基准折现率均值，用Crystal Ball软件随机生成5 000个离散系数为0.75，服从Gamma随机分布的随机数。

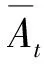
(8)

图5 长期条件下r2 等效值走势图

(3) 由折现系数期望值拟合出莱布森离散型折现函数，见即准双曲线函数表达式，拟合判定系数为R2>0.9，函数图象如图6所示。

(9)

(4) 相同方法，令r1=9%，y=8%，分别测算折现率r1和y对应的折现效用函数

(10)

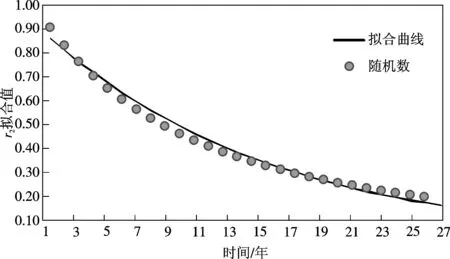
图6 r2 双曲折现拟合图

3． 两种折现函数的对比分析

用MATLAB运行得到双曲折现和指数折现现金流净现值差s与退出时间f的函数图形对比，如图7所示。两种折现方式的走势基本一致，都是随时间递减，即社会资本退出PPP项目时间越晚，财务可行性越小。采用准双曲折现时，整体评价结果要更乐观，退出的可行域更大；s递减的速率更小，有明显承台式停留；在f≥14后，由于m，循环次数为1，社会资本越晚退出财务上越可行，双曲折现的净现值有递增趋势。

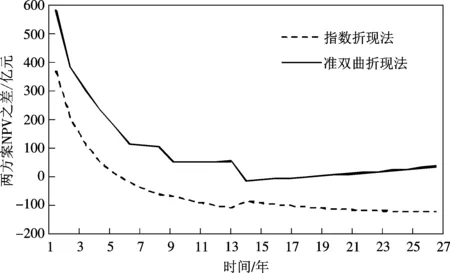
图7 双曲贴现与指数贴现对比f-s 函数图

五、 结 语

文章从社会资本角度出发，构建社会资本退出PPP项目的财务可行性研究框架，识别出影响社会资本退出的关键变量有退出PPP项目的交易成本、折现率、通货膨胀及退出时间。探讨折现率、交易成本等因素对社会资本退出时间的选择的影响，考虑到PPP寿命期长和行为经济学中时间偏好不一致，对指数折现和准双曲线折现两种方式的评价结果进行对比，经过模拟运算，可以看出运用递减的准双曲线折现模型进行测算是更为合理的。

经过模型推导和参数合理赋值后的模拟结果，得出以下结论及建议。

(1) 社会资本中期退出PPP项目的意愿或需求是可以满足的，财务方面具备一定可行性。

(2) 社会资本退出PPP项目的可行空间大小受折现率、二级市场社会资本折现率、通货膨胀率、退出的交易成本和退出时间等因素影响。二级市场社会资本要求的收益率越低，退出的交易成本越低，可选择的退出时间域越宽。社会资本退出的时间越早，资金利用率越高，财务越可观。

(3) PPP项目寿命期长，进行财务评价时不可忽视决策者的时间偏好不一致现象，运用准双曲折现率折现这种方式，更能准确体现行为人耐心递减，希望尽早获取投资收益的心态。因此建议社会资本在PPP项目前期，合理规划确定退出时机，有计划地尽早退出PPP项目，在特定项目阶段发挥自身优势；在项目中期，履行合约义务，保障项目质量，降低二级市场中接盘公司的预期风险，降低接盘公司的折现率，从而提高自身收益；在项目后期，利用二级市场信息透明化，降低退出交易成本。

[1] Demirag I，Khadaroo I，Stapleton P，et al．Public Private Partnership Financiers’Perceptions of Risks[R]．Institute of Chartered Accountants of Scotland，2010．

[2] Weber F．Simulation-based valuation of project finance：Does model complexity really matter? [J]．SocialScienceElectronicPublishing，2010，12(5)：118-139．

[3] Albornoz V A C D，Solio A S．Is there room for a PPP secondary market? Financial analysis of the PPP transport sector[J]．JournalofManagementinEngineering，2014，31(5)：04014084．

[4] Esty B C．Improved techniques for valuing large-scale projects[J]．JournalofStructuredFinance，1999(1)：9-25．

[5] Thaler R H, Shefrin H M. An economic theory of self-control[J].SocialScienceElectronicPublishing, 1981, 89(2):392-406.

[6] Prelec D．Decreasing impatience：Definition and consequences[J]．HarvardBusinessSchoolWorkingPaper，1989，10(1)：90-105.

[7] Parker C．The Implications of Discount Rate Reductions on Transport Investments and Sustainable Transport Futures[R]．New Zealand Transport Agency Research Report，2009：1-156．

[8] Arrow K J，Cropper M L，Gollier C，et al．Should governments use a declining discount rate in project analysis? [J]．ReviewofEnvironmentalEconomicsandPolicy，2014，8(2)：145-163．

[9] 胡江碧，刘 妍，高玲玲．桥梁全寿命周期费用折现率分析[J]．公路，2008(9)：363-367．

[10] 孙燕芳，张连营．基于可持续发展观的公共项目投资社会折现率的确定[J]．经济体制改革，2012(3)：117-120．

[11] Loewenstein G，Prelec D．Anomalies in intertemporal choice：Evidence and an interpretation[J]．QuarterlyJournalofEconomics，1992，107(2)：573-597．

[12] Prelec D．Decreasing impatience：A criterion for non-stationary time preference and “hyperbolic”discounting[J]．TheScandinavianJournalofEconomics，2004，106(3)：511-532．

[13] Dailami M，Lipkovich I，Van Dyck J．INFRISK：A computer simulation approach to risk management in infrastructure project finance transactions[R]．Policy Research Working Paper，1999．

[14] Araujo S，Sutherland D．Public-private partnerships and investment in infrastructure[J]．SocialScienceElectronicPublishing，2010(1)：3-44．

[15] Weitzman M L．Gamma discounting[J]．AmericanEconomicReview，1998，91(1)：260-271．

[16] 邵颖红，黄渝祥．公共项目的经济评价与决策[M]．上海：同济大学出版社，2010．

[18] Esty B C．Why study large projects? An introduction to research on project finance[J]．EuropeanFinancialManagement，2004，10(2)：213-224．